數位影像處理筆記
- 一,緒論
- 二,數位影像基礎
- 三,灰度變換與空間濾波
- 四,頻率域濾波
- 五,影象復原與重建
- 六,彩色影象處理
- 八,影象壓縮和水印
- 參考資料
本文章是對《數位影像處理》書的學習筆記,不涉及具體程式碼,主要是原理概述和公式描述,及概念理解。學習數位影像處理能讓我們更深入理解計算機視覺領域的內容。
一,緒論
1.1, 什麼是數位影像處理
一副影象可以定義為一個二維函數 \(f(x,y)\),其中 \(x\) 和 \(y\) 是空間(平面)座標,任意一對空間座標 \((x,y)\) 處的幅度值 \(f\) 稱為影象在該座標點的強度或灰度。當 \(x,y\) 和灰度值 \(f\) 都是有限的離散量時,我們稱該影象為數位影像。數位影像處理是指藉助於數位計算機來處理數位影像。注意,數位影像由有限數量的元素組成,每個元素都有一定的位置和數值,這些元素稱為畫素。
影象處理止於何處或其他相關領域(如影象分析和計算機視覺)始於何處,目前人們的看法並不一致。在本書中,將數位影像處理定義為其輸入和輸出都是影象的處理。
1.2,數位影像處理的起源
略。
1.3,數位影像處理技術應用範例
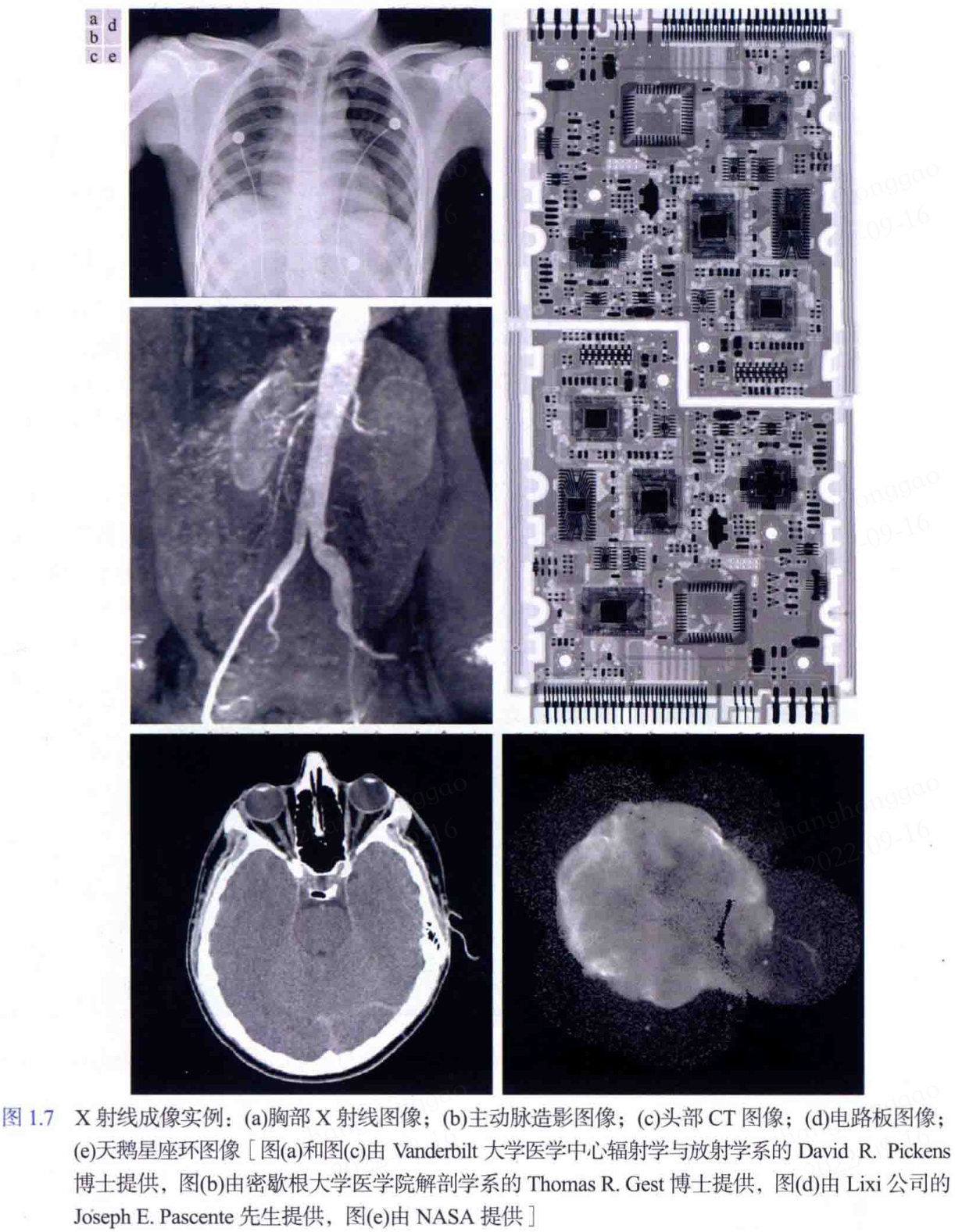
目前數位影像處理已經應用於各行各業,在本書中,為了更簡單表述,將數位影像處理的應用領域根據數位影像源分類(如可見光或 X 射線等)。目前最主要等影象源是電磁波譜,其他重要的影象源還有聲波、超聲波和電子(電子顯微鏡中所用的電子束)。
基於電磁波譜輻射的影象是我們比較數位的影象,比如 X 射線和可見光譜段的影象。電磁波可定義為以各種波長傳播的正弦波,或可視為無質量的粒子流,每個粒子流以波的形式傳播並以光速運動。每個無質量的粒子都包含一定的能量(或一束能量),每束能量稱為一個光子。根據每個光子的能量對光譜波段進行分組,得到圖 1.5 所示的光譜,其範圍從伽瑪射線(最高能量)到無線電波(最低能量)。

根據以上電磁波譜,可得到以下電磁波譜成像:
- 伽瑪射線成像:伽瑪射線成像的主要用途包括核醫學和天文觀測。在核醫學中,方法是將放射性同位素注入人體,同位素衰變時會發射伽瑪射線,影象則由伽瑪射線檢測器收集到的放射線產生。下圖展示了一幅使用伽瑪射線成像得到的人體骨骼掃描影象。
- X 射線成像:X 射線成像除了應用於醫學診斷,還被廣泛應用於工業和其他領域,如天文學。
- 紫外波段成像。
- 可見光和紅外波段成像:應用領域最廣,如光學顯微鏡、遙感影象、氣象監測影象、工業自動視覺檢測等。
- 微波波段成像:主要應用是雷達。
- 無線電波成像:應用領域如醫學等磁共振成像(MRI)。
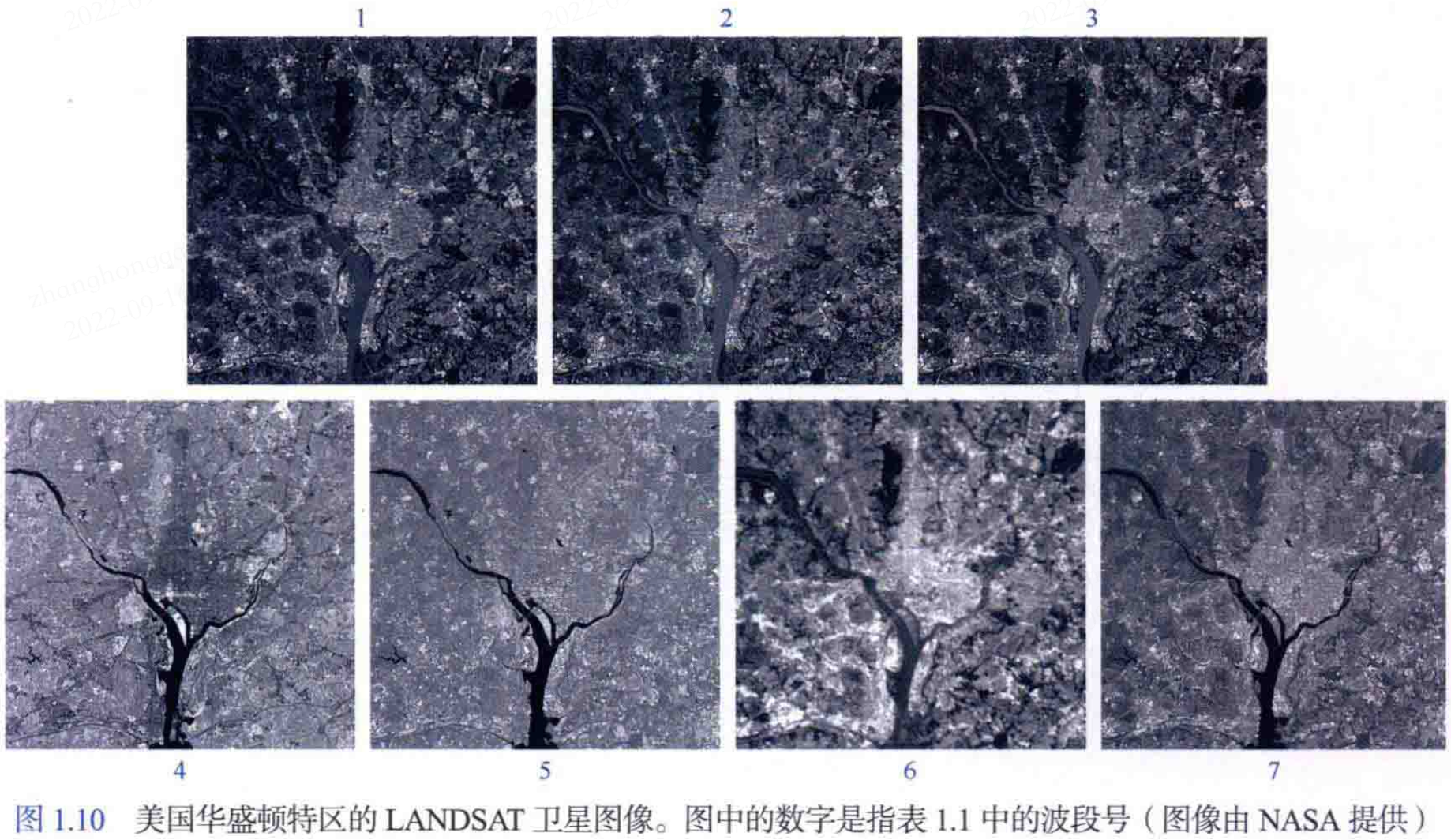
一些影象範例效果圖如下圖所示。
1.4,數位影像處理的基本步驟
本書中的數位影像處理步驟如下圖所示。
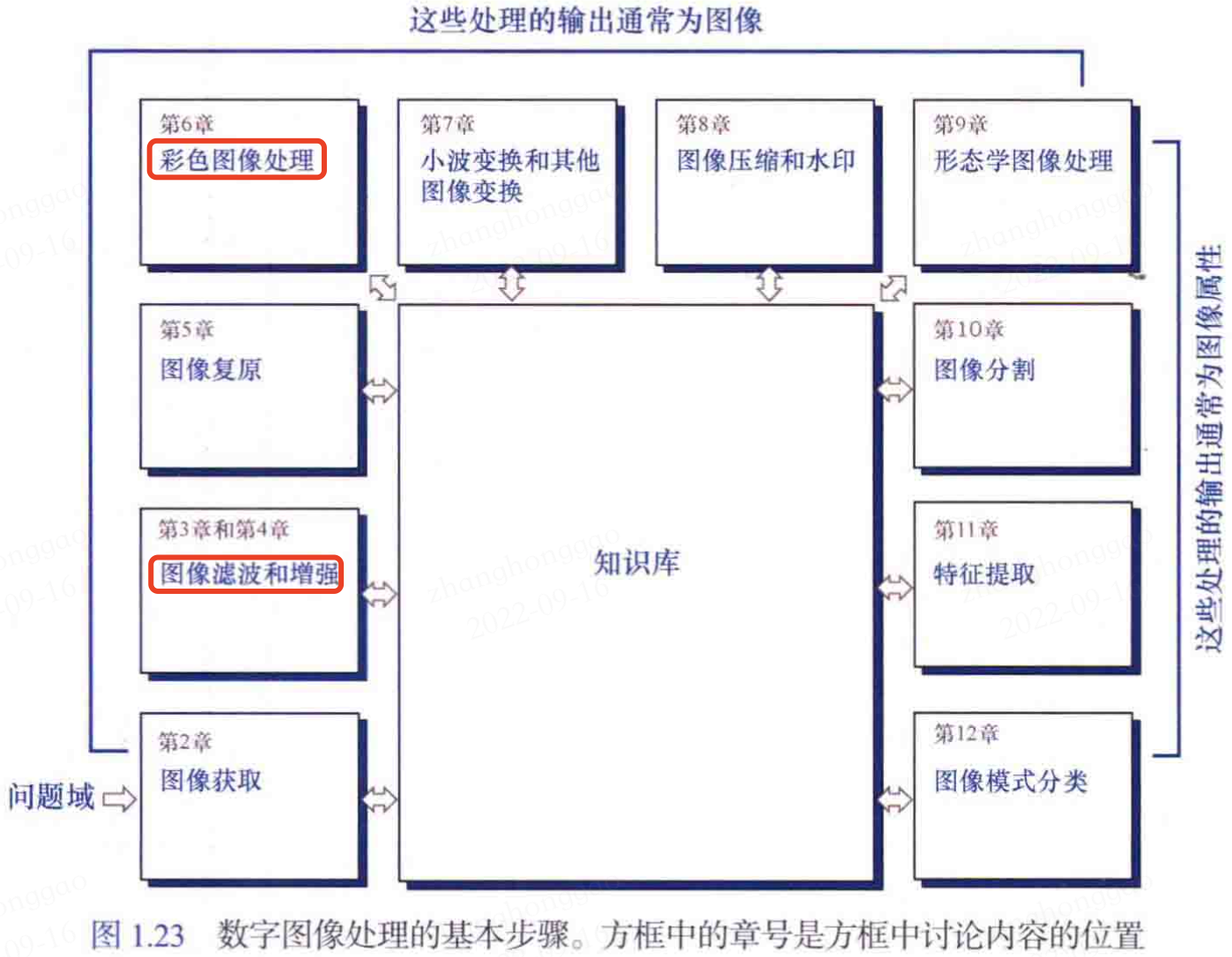
1.5,影象處理系統的組成
略。
二,數位影像基礎
相機成像的原理:針孔相機( Pinhole Camera )通過投影變換,可以將三維相機(Camera)座標轉換為二維的影象座標,這個變換矩陣是相機的內在屬性,稱為相機內參(Camera Intrinsic) K。
yaw 航向角,pitch 俯仰角,roll 翻滾角。
2.1,視覺感知要素
通過這節內容瞭解影象被人類感知的基本原理及人類視覺的物理限制。
2.1.1,人眼的結構
下圖顯示了人眼的簡化剖面圖。
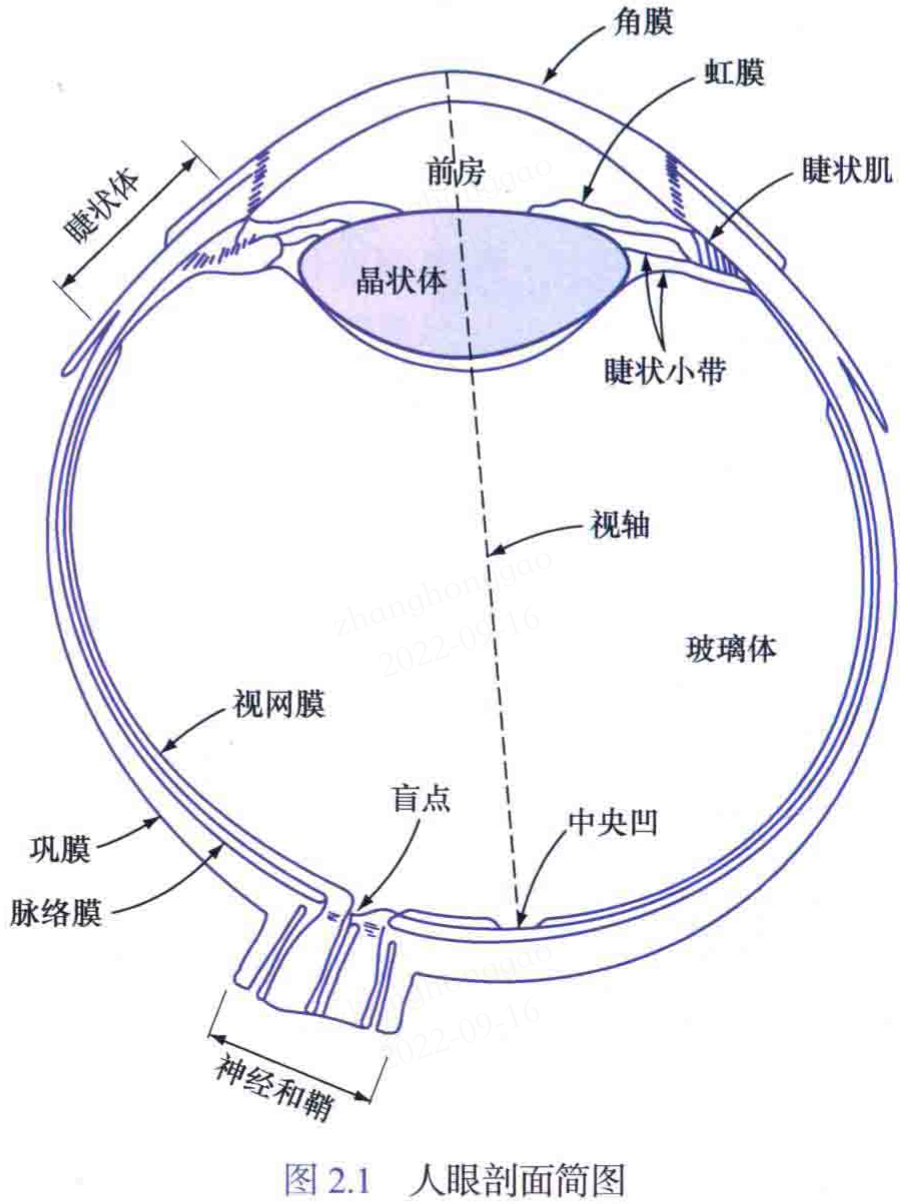
眼鏡最靠內部的膜是視網膜,它佈滿了整個後部的內壁。眼睛聚焦時,來自物體的光在視網膜上成像。模式視覺由分佈在視網膜表面上的哥哥分立光感受器提供,分為兩類:錐狀體和桿狀體。錐狀體視覺稱為明視覺或亮視覺。桿狀體視覺稱為暗視覺或微光視覺。
2.1.2,人眼中影象的形成
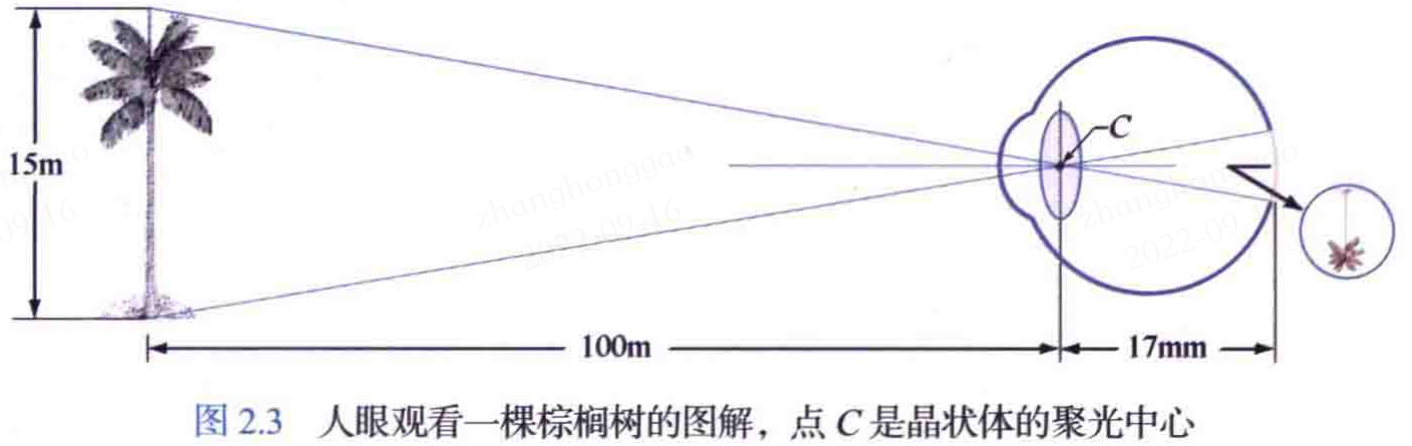
數碼相機中,既有固定焦距的鏡頭,也有可變焦距的鏡頭,不同距離的聚焦時通過改變鏡頭和成像平面之間的距離來實現的。在人眼中,晶狀體和成像區域(視網膜)之間的距離是固定的,正確的聚焦是通過改變晶狀體的形狀得到(遠離壓扁晶狀體,接近目標則加厚晶狀體),晶狀體中心和沿視軸的視網膜之間的距離約為 17mm,焦距範圍為 14~17 mm。下圖所示的幾何關係說明了在視網膜上所形成的影象的尺寸。令 \(h\) 表示視網膜影象中物體的高度, 根據幾何關係:\(15/100 = h/17\),得到 h = 2.5 mm。
2.1.3,亮度適應與辨別
以下兩種現象表明人眼的感知亮度不是十幾灰度的簡單函數:
- 「下衝」或「上衝」現象(馬赫帶效應)。
- 同時對比現象。

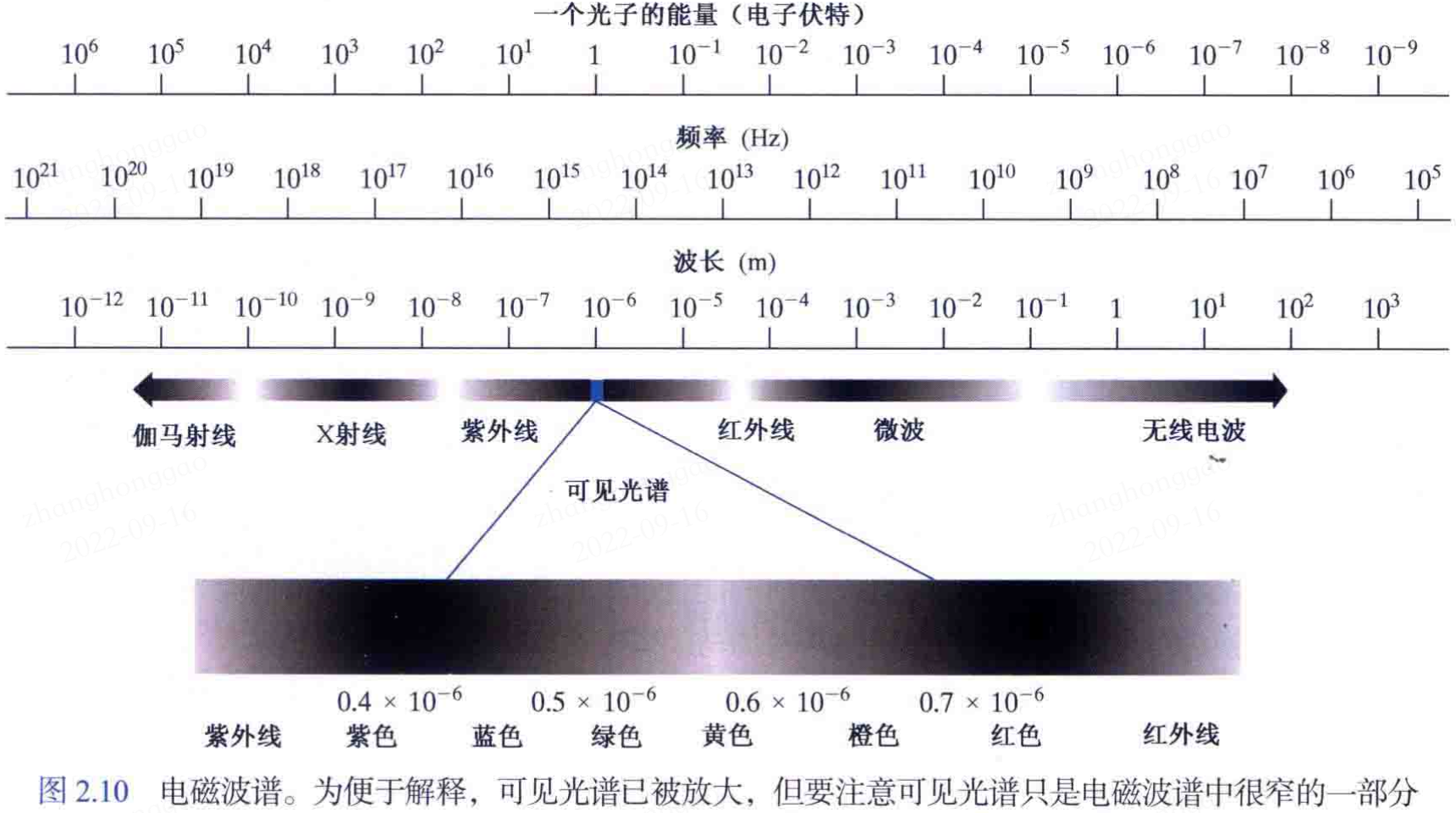
2.2,電磁波譜
更詳細的電磁波譜圖如下圖所示。波長常用的單位是米(m),常用的單位是微米(表示為 \(\mu m\),\(1\mu m=10{^-6}m\))。
- 感知的物體顏色由物體反射的光的性質決定。
- 沒有顏色的光稱為單色光或無色光。
- 彩色光源的三個屬性:頻率、輻射、光通量和亮度。
2.3,影象感知與獲取
將照射能量轉換為數位影像主要由三種感測器設定:
- 使用單個感測器獲取影象
- 使用條帶感測器獲取影象:如磁共振成像(MRI)和正電子發射斷層成像(PET)等。
- 使用陣列感測器獲取影象: 如單反相機和手機相機。
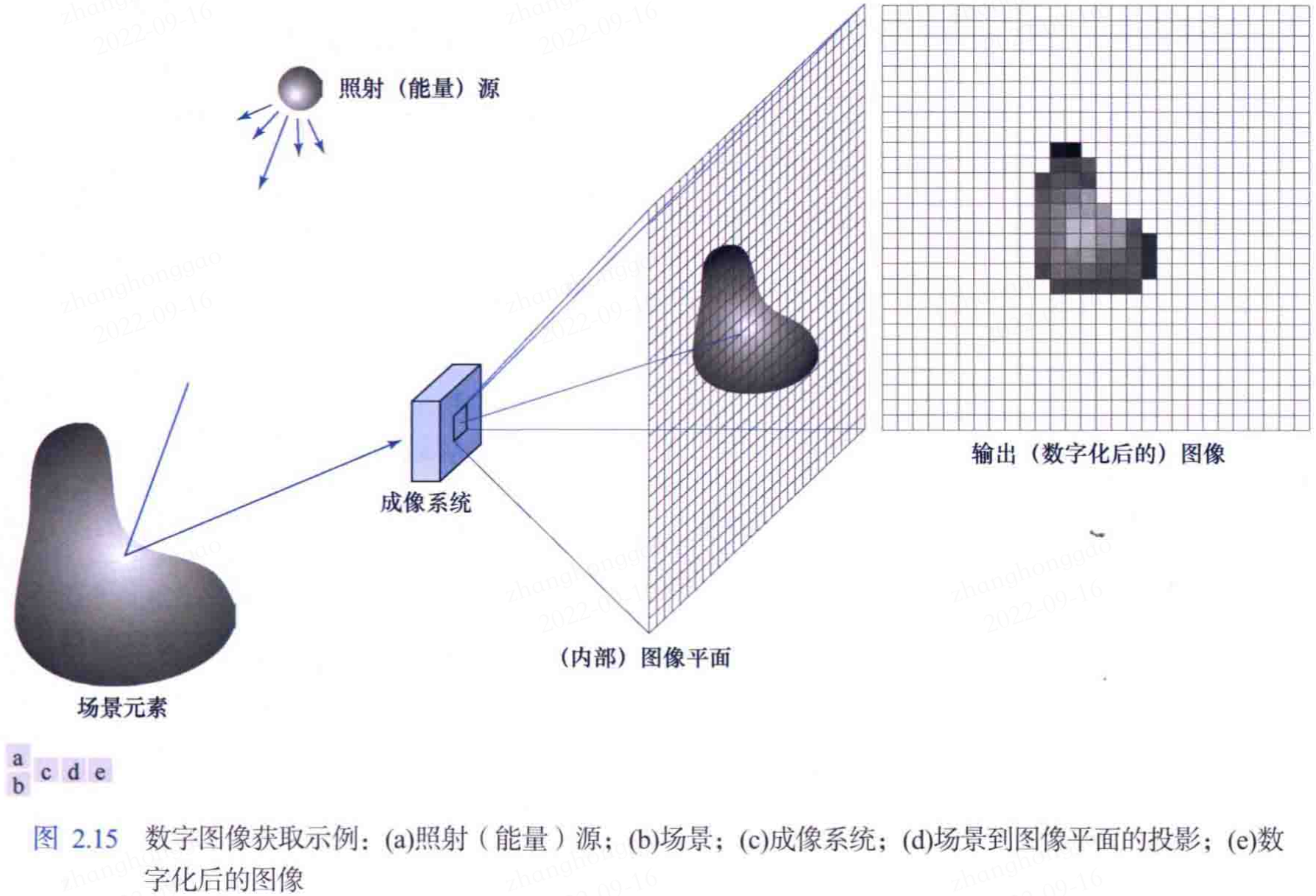
2.3.1,一個簡單的成像模型
如 1.1 節所述,我們用形如 \(f(x,y)\) 的二維函數來表示影象,在空間座標 (x,y) 處 \(f\) 的值是一個標量,其範圍 \(0\leq f(x,y) < \infty\)。
2.4,影象取樣和量化
多少感測器的輸出都是連續的電壓被判刑,這些波形的幅度和空間特性都與正被感測的物理現象相關。要產生一幅數位影像,就需要把感測得到的連續資料轉化為數位形式,這包括兩個步驟:取樣和量化。
2.4.1,取樣和量化的概念
一幅連續影象 \(f\),對座標值進行數位化稱為取樣(或取樣),對幅度值進行數位化稱為量化。
2.4.2,數位影像表示
在計算機中,數位影像可用一個 \(M\times N\)矩陣表示,影象長為 \(M\),寬為 \(N\),矩陣中的每個元素即為影象的畫素。
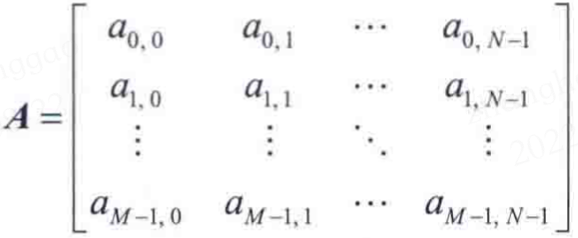
2.5,畫素間的一些基本關係
- 畫素的相鄰畫素
- 鄰接、連通、區域和邊界
- 距離測度:兩個畫素的距離,通過歐幾里得(歐式)距離計算:\(D(p,q) = \sqrt{[(x-u)^2 + (y-v)^2]}\)
2.6,數位影像處理所用的基本數學工具
2.6.1,對應元素運算和矩陣運算
涉及一幅或多幅影象的對應元素運算是逐個畫素操作的,有因為在數位影像處理中,影象可以等效為矩陣,所以影象之間的運算是可以用矩陣理論執行的。
2.6.2,線性運算和非線性運算(一般兩個影象之間)

線性運算更為重要,包含了大量適用於影象處理的理論與實踐成果;非線形運算範圍比較有限。
2.6.3,數位影像處理數學工具-算術運算(一般兩個影象之間)
算術運算常用在特定的天文、醫學等領域,將兩幅影象經過算術運算從而得到更為清晰的影象,兩幅影象的算術運算表示如下:
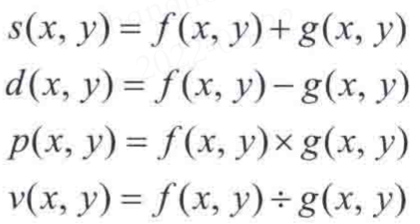
這些加減乘除運算都是對應的畫素運算,算術運算一般有以下應用:
- 使用影象相加(平均)降低噪聲。
- 使用影象相減比較影象。
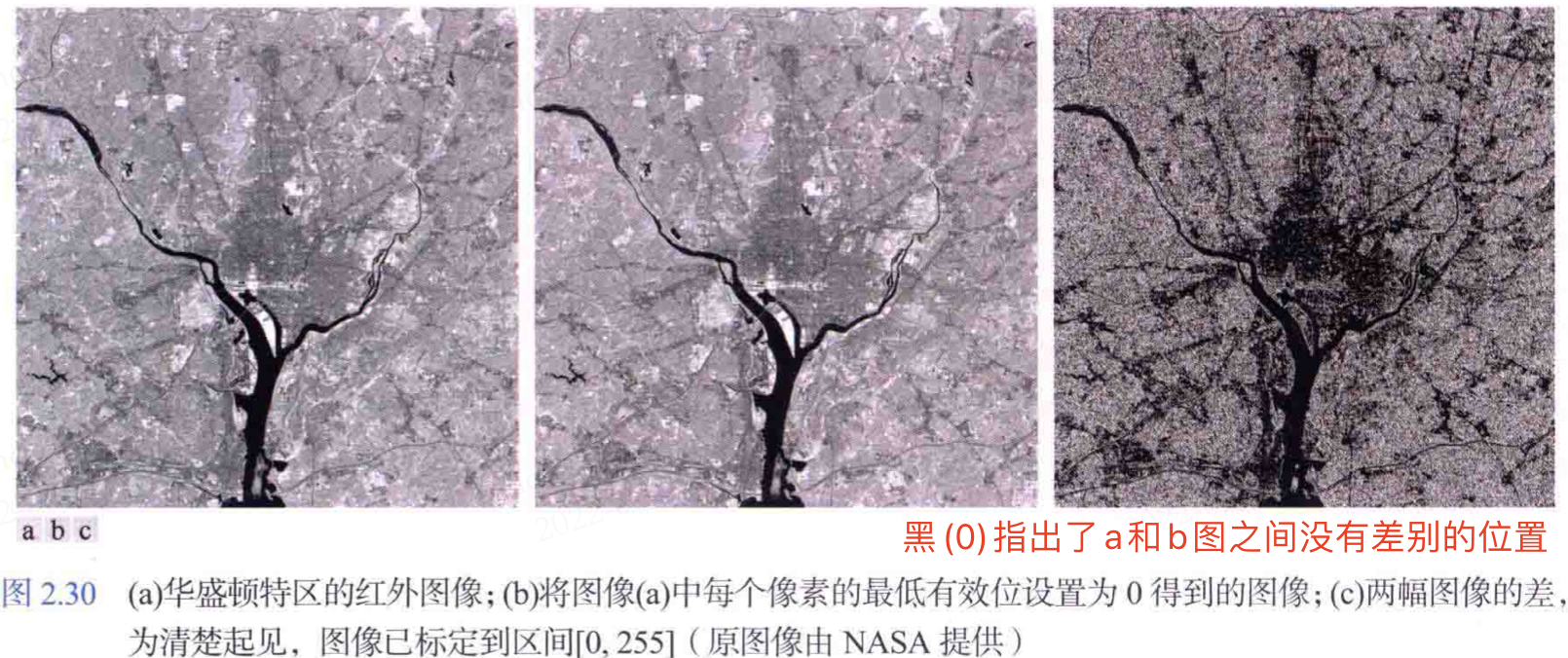
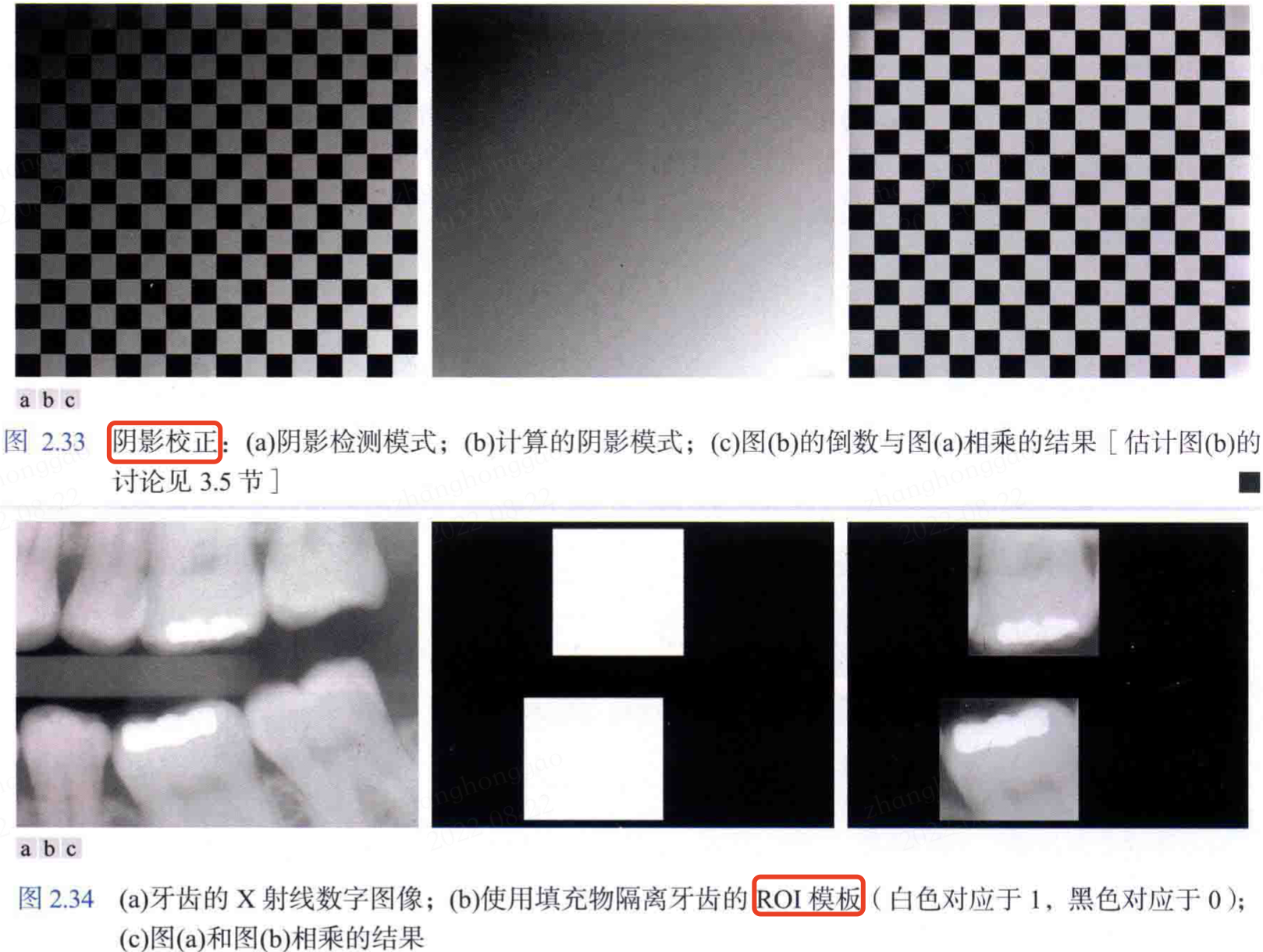
- 使用影象相乘/相除校正陰影和模板。
3 種演演算法運算的實際應用效果對比圖如下所示:

2.6.4,集合運算和邏輯運算(一般兩個影象之間)
注意這裡的集合運算針對的是二值影象,或者影象中所有畫素具有相同的灰度值且。
假設有兩個集合 A 和,在數位影像處理中常見的集合運算有:
- 交集運算: \(C = A\cap B\),滿足交換律、結合律和分配律。
- 並集運算: \(C = A\cup B\)。
如果想要知道一幅二值影象中的兩個目標 A 和 B 是否重疊,可通過計算 A\cap B$。如果結果不是空集,則可確定兩個目標的某些元素是有重疊的。
2.6.5,空間運算(單幅影象)
空間運算是直接對單幅影象的畫素執行數學操作,分為三類:(1)單畫素運算;(2)領域運算;(3)幾何空間運算。
2.6.5.1,單畫素操作
用一個變化函數\(T\)改變影象中各個畫素的灰度:
上述公式對應單畫素操作,\(z\)是原影象中畫素的灰度,\(s\)是處理後影象中對應畫素的(對映)的灰度。
2.6.5.2,領域運算
令 \(S_{xy}\) 代表影象 \(f\)中以任意一點 \((x,y)\) 為中心的一個鄰域的做標集,領域處理後,輸出影象\(g\)中的相同座標處會生成一個新的畫素,該畫素的值由輸入影象中鄰域畫素的規定運算和集合\(S_{xy}\)中的座標確定。假設領域運算對應的是計算大小為\(m\times n\)、中心為\((x,y)\)的矩形領域中畫素的平均值,且這個區域中的畫素座標是集合\(S_{xy}\)的元素,那麼其對應的領域運算公式如下:
上述公式中,\(r\)和\(c\)是畫素的行和列座標,屬於集合\(S_{xy}\),影象\(g\)是通過移動座標\((x,y)\),使得領域的中心逐個移過影象\(f\)中的所有畫素,然後在每個新位置都重複這一領域運算得到,對應的示意圖如下:
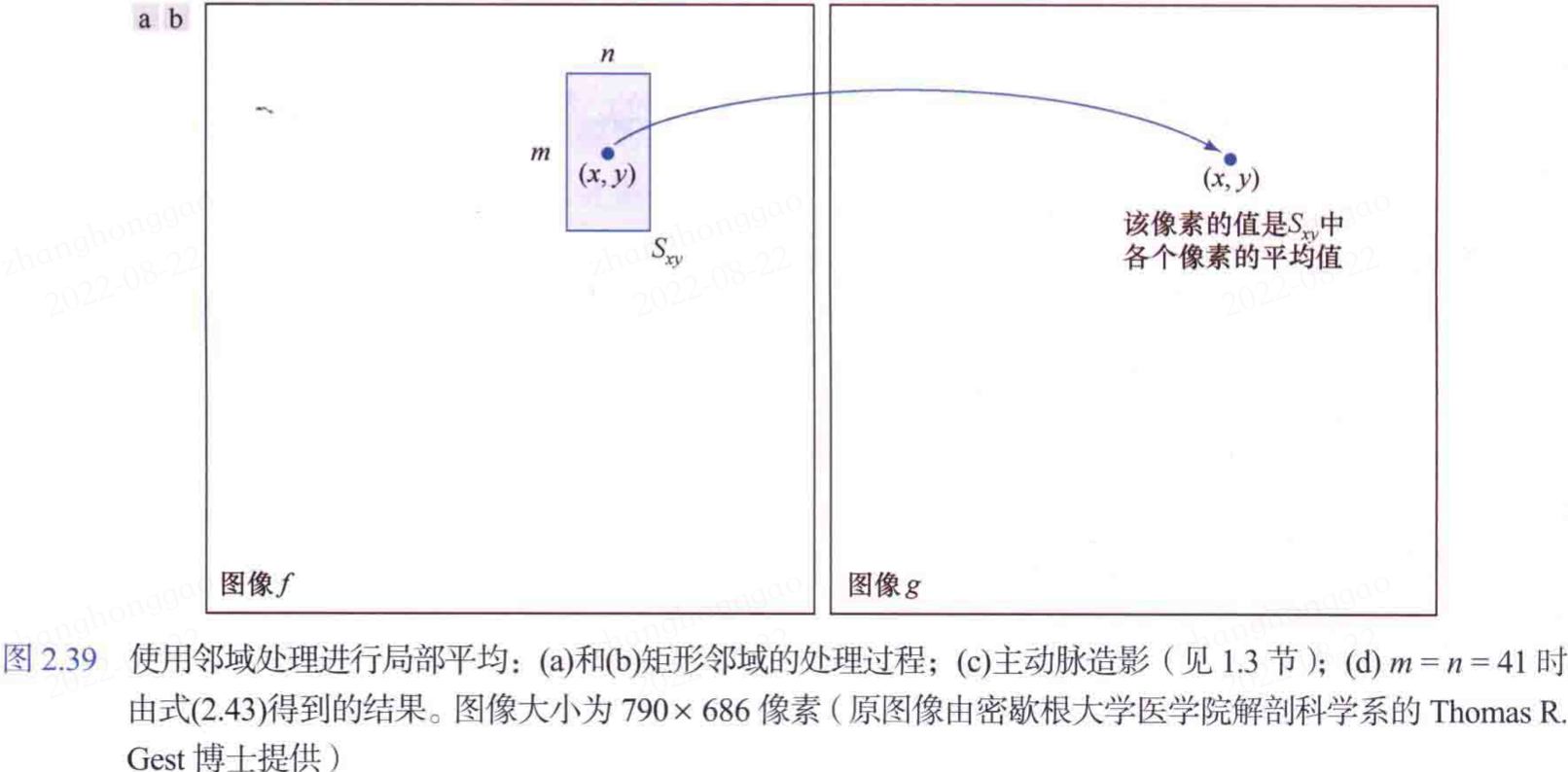
簡單理解所謂的領域運算就是對特定 roi 區域的所有畫素,做特定操作,而這個操作就是以指定位置 \((x,y)\) 為中心,鄰域範圍為 \(m\times n\),對這個範圍內的畫素取平均/求和/最大值/等。
典型的就是
CNN模型中折積層的濾波器操作。
2.6.5.3,幾何變換
幾何變換即改變影象中畫素的空間排列,由兩種基本運算組成:
- 座標的空間變換;
- 灰度內插,即為變換後的畫素賦灰度值(灰度圖)。
座標變換公式可表示為:

最為重要的是放射變換,它包括縮放變換、平移變換、旋轉變換和剪下變換。式(2.44)無法表示平移變換(需要在公式右側新增一個常數二維向量),所以需將上式升級為,如下所示的齊次座標變換。
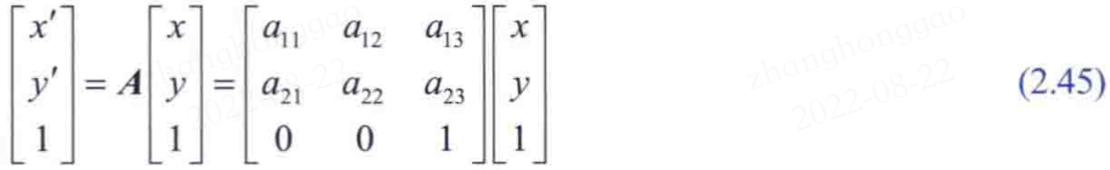
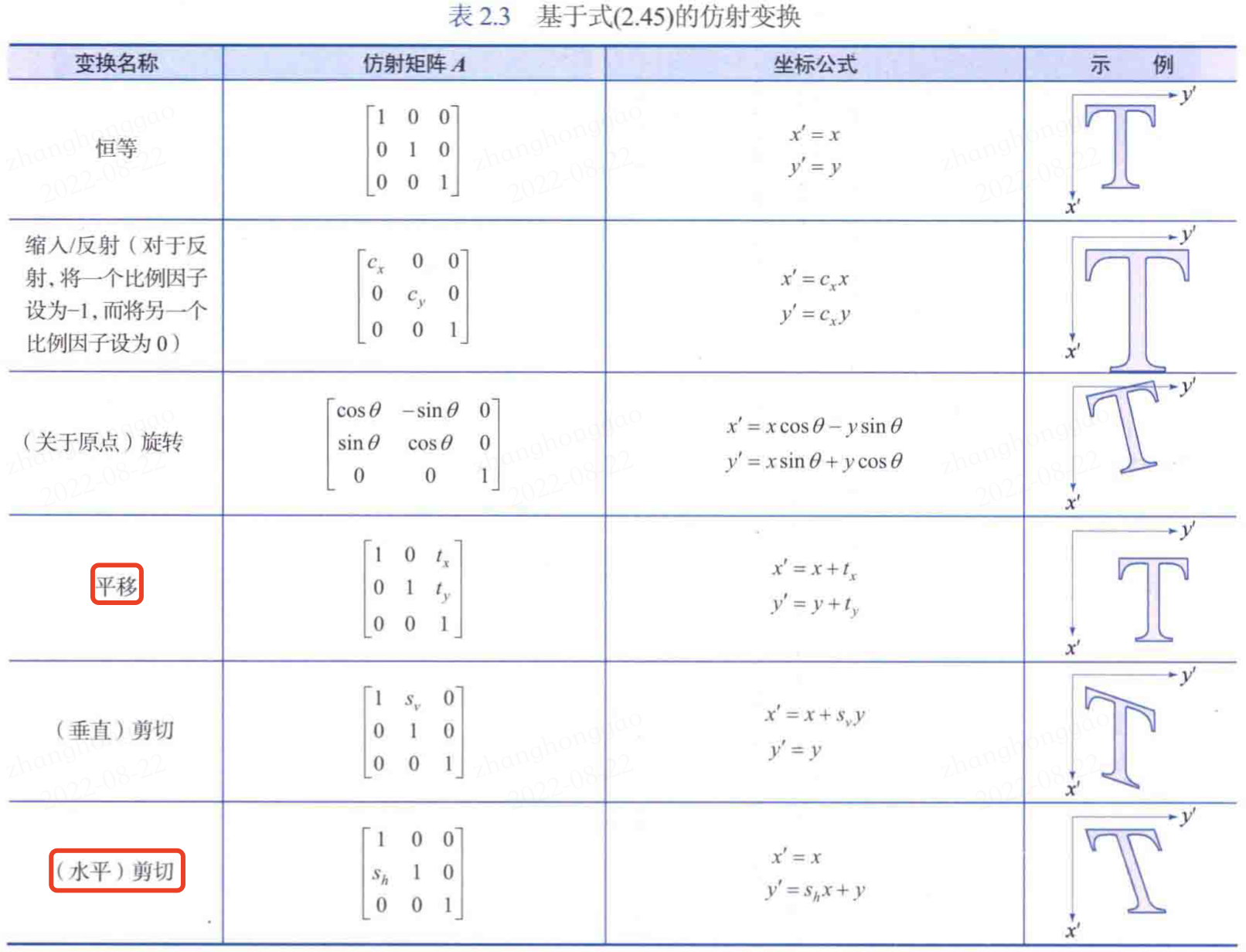
常見影象幾何操作對應的仿射矩陣 A 、變換座標公式以及示意圖如下表所示:
三,灰度變換與空間濾波
空間域指的是影象平面本身,空間域中的影象處理方法是直接對影象中的畫素進行處理。空間域影象處理的兩個主要類別是:
- 灰度變換: 如對比度處理和影象閾值處理等任務,直接對影象的給個畫素進行操作。
- 空間濾波: 如影象平滑和銳化,對影象中的每個畫素的鄰域進行操作。
3.1,背景
本章中討論的所有影象處理技術都是在空間域中實現的,所謂的空間域即包含影象中畫素的平面。空間域技術直接操作影象中的畫素,而頻率域技術操作的是影象的傅立葉變換而非影象本身。
由影象的座標張成的實平面部分稱為空間域,\(x\)和\(y\)稱為空間變數或空間座標。
儘管灰度變換和空間濾波的應用範圍廣泛,但本書中的大多數例子是關於影象增強的。所謂影象增強技術,是為了某些特定應用對原影象進行加工的技術,不具備通用性。
3.2,一些基本的灰度變換函數
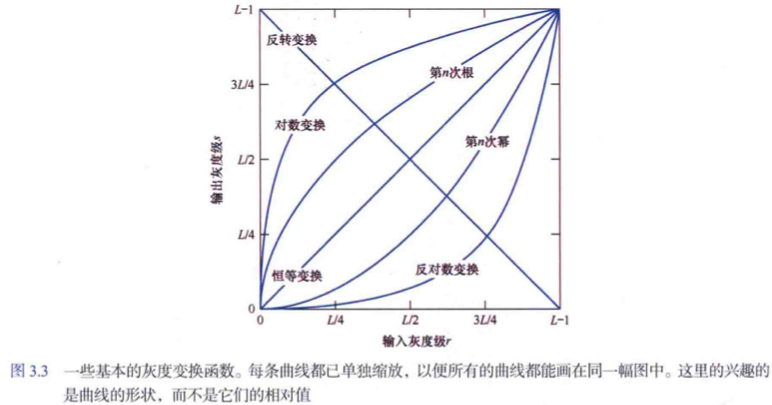
通過灰度變換函數\(T\)將原來的畫素值\(r\)對映為畫素值\(s\)。灰度變換中常用的 3 類基本函數是線性(反轉和恆等變換: 輸入灰度和輸出灰度相同)函數、對數(對數和反對數變換)函數和冪律(n次冪或n次根)函數。
3.2.1,影象反轉
假設原影象畫素值為\(r\),灰度級在區間為 [0, L-1],則起反轉後的影象形式為
影象反轉範例效果圖如下所示:
3.2.2,對數變換
對數變換的形式如下:
圖3.3中對數曲線的形狀表明,對數變換會將輸入中範圍較窄的低灰度值對映為輸出中範圍較寬的灰度級。例如區間 [0, L/4]中的輸入灰度級對映到 [0, 3L/4] 中的輸出灰度級;相反輸入中的高灰度級被對映為輸出中範圍較窄的灰度級。
3.2.3,冪律變換(伽瑪變換)
冪律變換形式如下:
3.2.4,分段線性變換函數
- 對比度拉伸
對比度拉伸可以拓展影象中的灰度級範圍,使其覆蓋記錄媒介或顯示裝置的整個理想灰度範圍。

- 灰度級分層
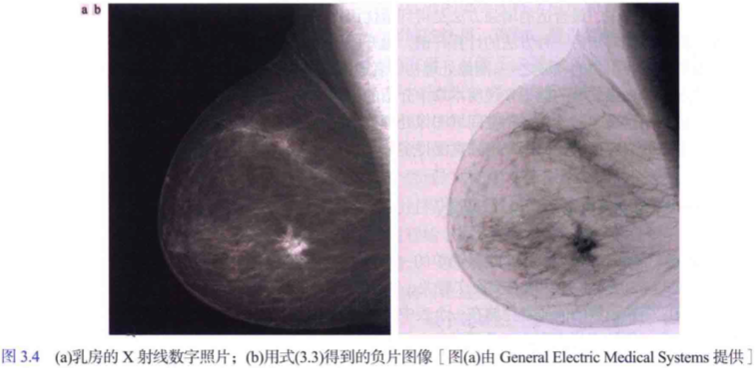
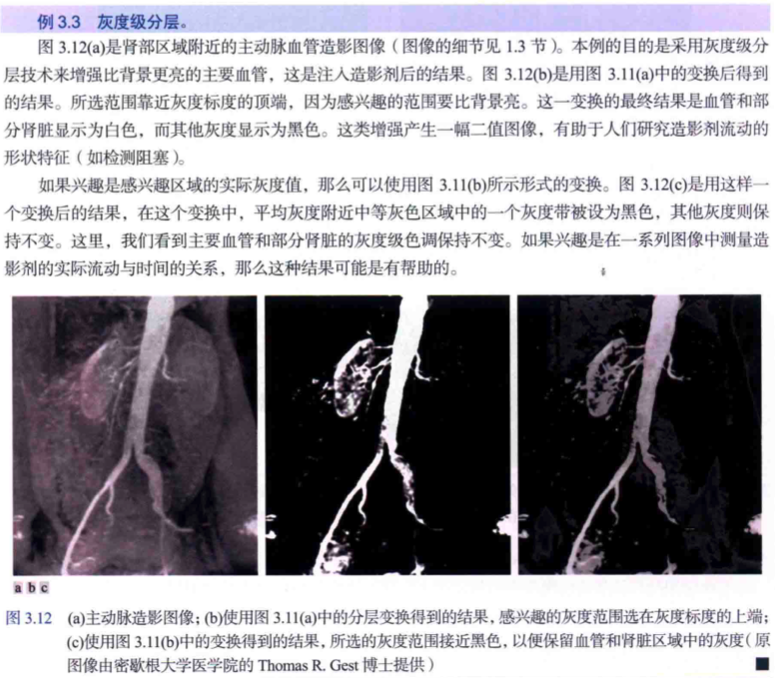
有些影象增強應用的目的是為了突出影象中的特定灰度空間,比如增強衛星影象中的特徵、增強 X 射線影象中的缺陷等。灰度級分層可以基於兩個基本方法及其變體來實現。
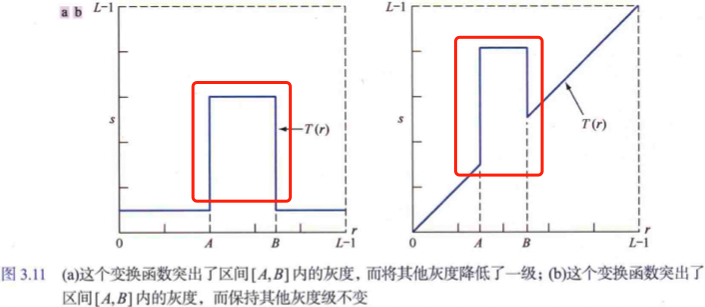
- 一種方法是將感興趣範圍內的所有灰度值顯示為一個值(如白色),而將其他範圍的灰度值顯示為另一個值(黑色),這種變換會得到一個二值影象。
- 另一種方法是基於圖3.11(b)中的變換,使期望的灰度範圍變亮(或變暗),但保持影象中的其他灰度級不變。
灰度級分層的實際應用例子如下圖所示
我個人感覺這個應用得根據實際專業場景結合起來使用,難點在於灰度級範圍的選擇。
- 位元平面分層
略。
3.3,直方圖處理
令 \(r_k(k = 0,1,2...L-1)\) 表示一幅\(L\)級灰度數位影像 \(f(x,y)\) 的灰度。 \(f\) 的非歸一化直方圖定義為
式中,\(n_k\)是\(f\)中灰度為\(r_k\)的畫素的數量,並且細分的灰度級稱為直方圖容器。類似地,歸一化直方圖定義為
式中,\(M\) 和 \(N\) 分別是影象的行數和列數。對\(k\)的所有值,\(p(r_{k})\)的和總是 1.
下顯示了具有 4 個基本灰度特性的影象:
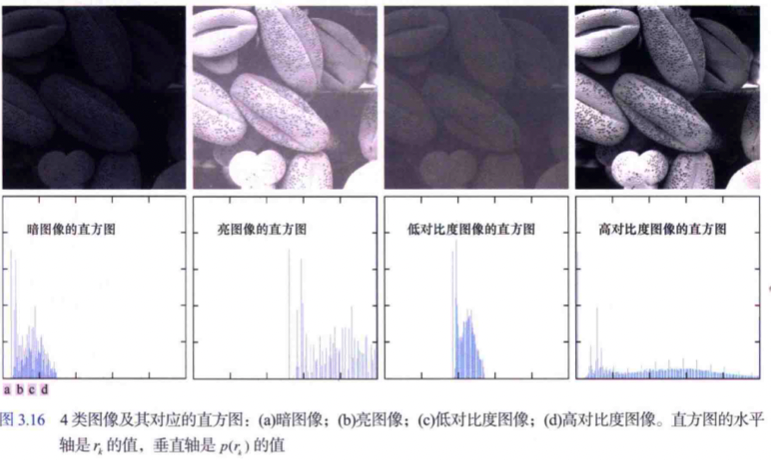
從上圖的分析我麼可以得出這樣一個結論: 即畫素佔據整個灰度級範圍並且均勻分佈的影象,將具有高對比度的外觀和多種灰色調。最終結果將是顯示了大量灰度細節並具有高動態範圍的一副影象。
3.3.1,直方圖均衡化
1,直方圖均衡化所用的變換函數如下(推導過程複雜,跳過,感興趣的可以閱讀原書瞭解過程)
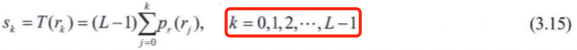
2,直方圖均衡化的目的是為了生成一幅具有均勻直方圖的輸出影象。
3,直方圖均衡化效果範例如下圖所示:
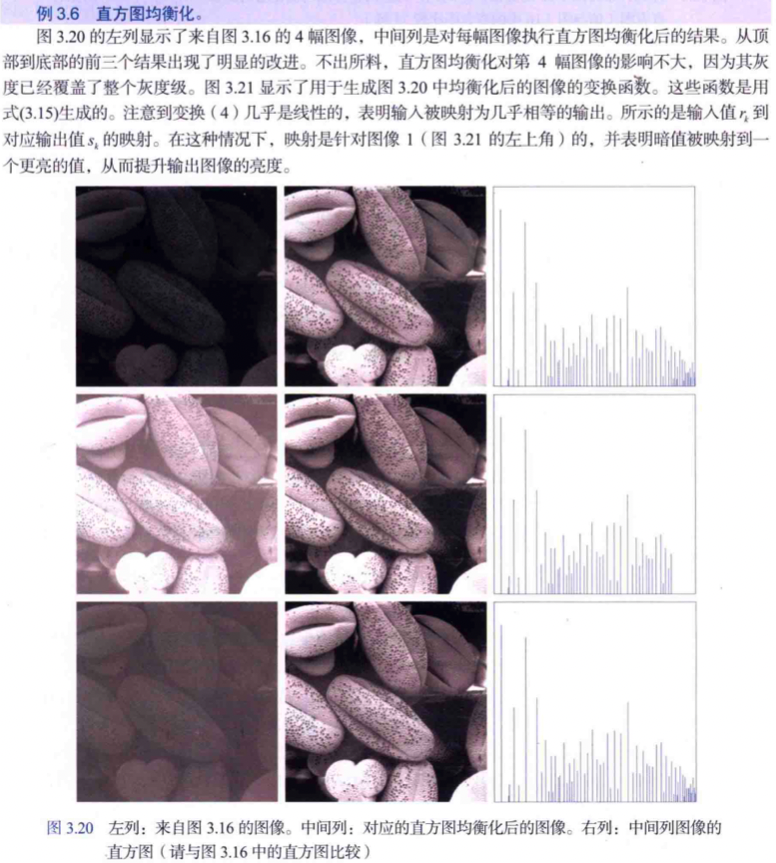
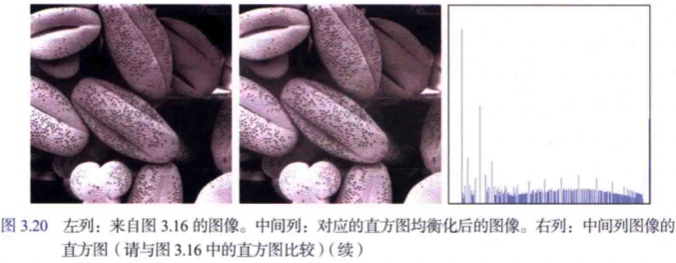
直方圖均衡化效果總結分析:儘管 4 個直方圖都不同,但直方圖均衡化後的影象是很相似的,因為原來的 4 個圖的基本區別是對比度而非內容。
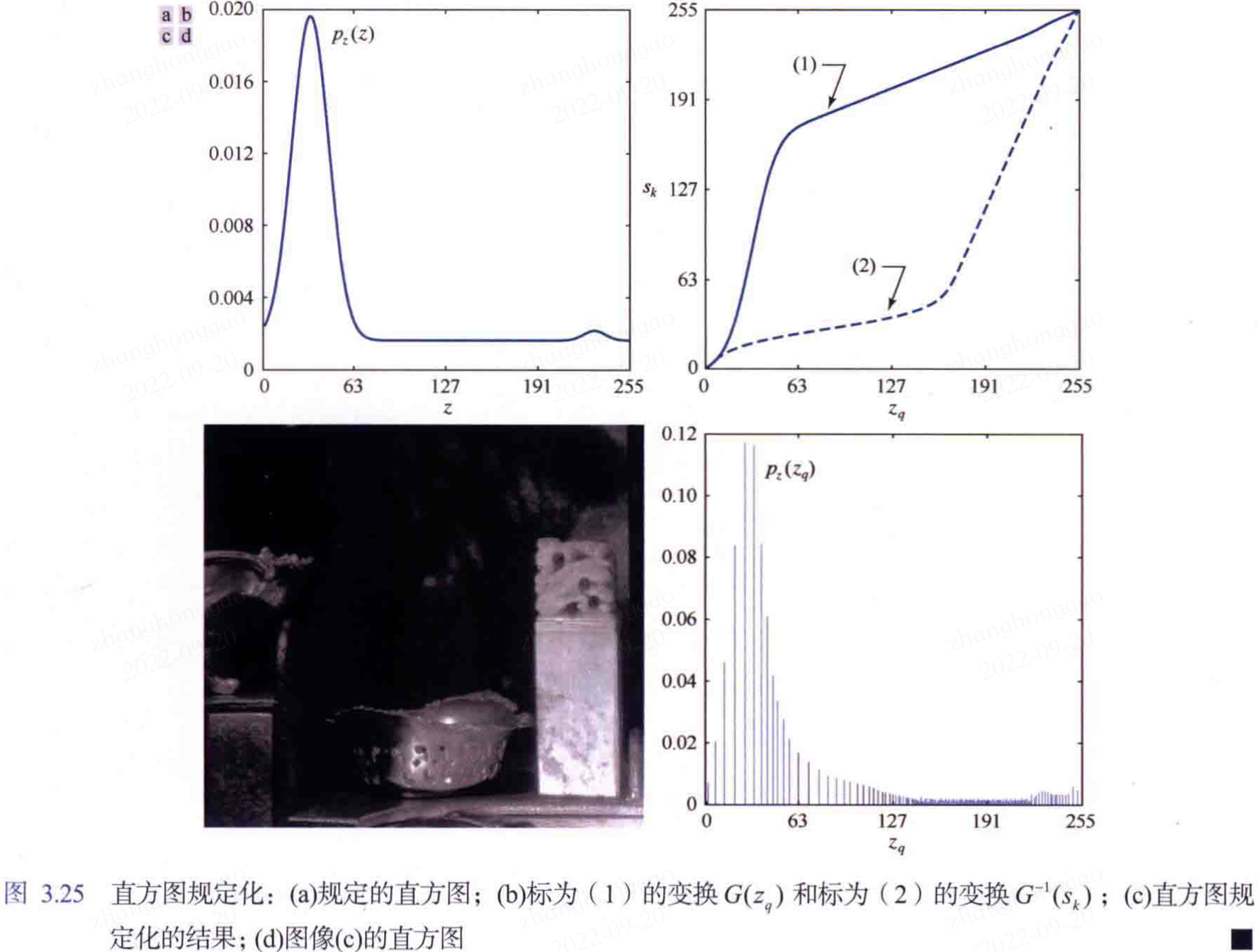
3.3.2,直方圖匹配(規定化)
直方圖匹配(規定化)定義:用於生成具有規定直方圖的影象的方法稱為直方圖匹配(規定化)。
直方圖規定化的推導過程較為複雜,請參考原書。本筆記中,直接看特定的一幅影象經過直方圖均衡化和規定化的對比結果。
1,直方圖均衡化後的效果圖如下所示(有噪聲):
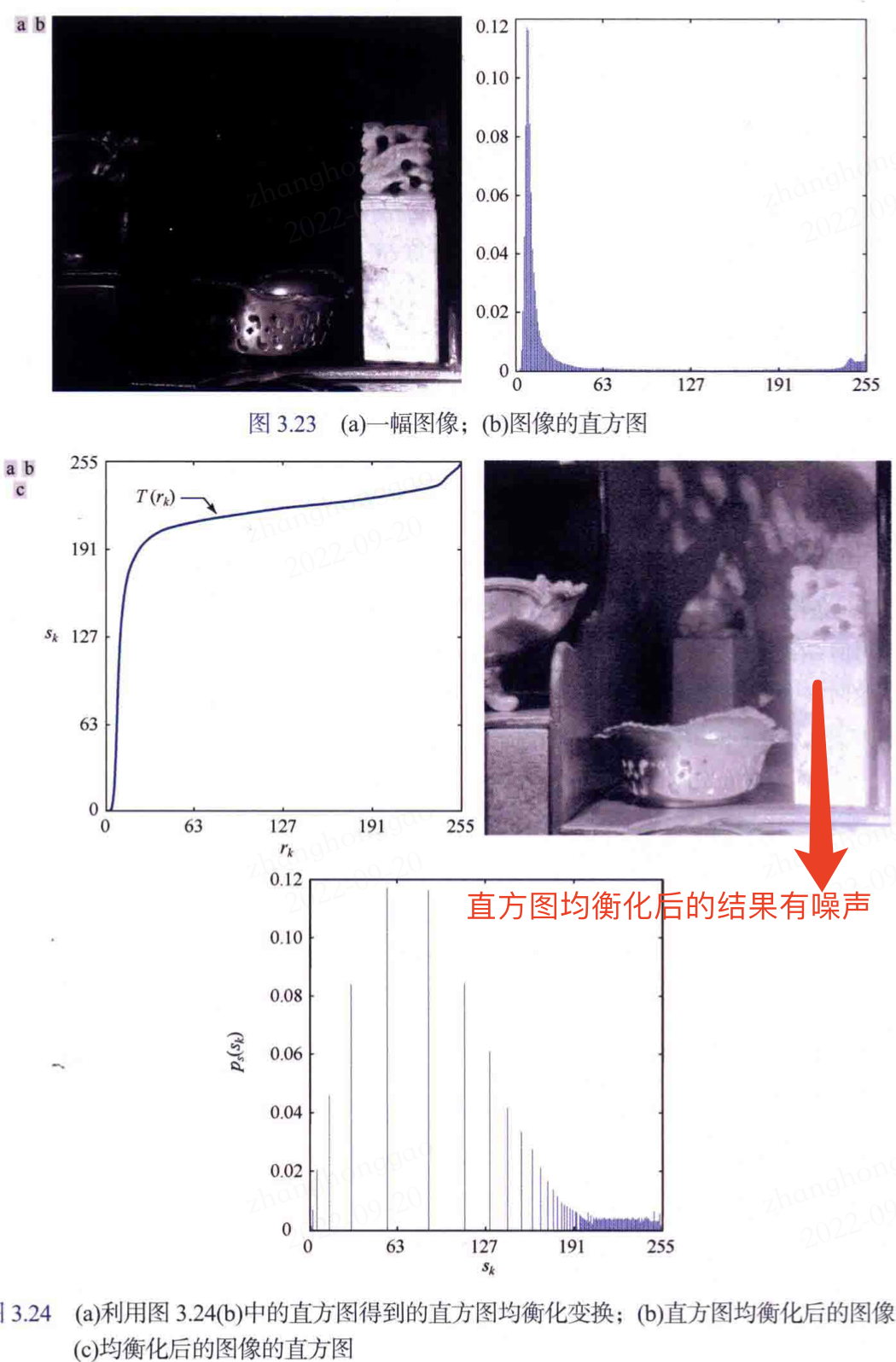
2,直方圖規定化後的效果圖如下所示(無噪聲):
3.3.3,區域性直方圖處理
直方圖均衡化和直方圖規定化的直方圖處理方法都是全域性性的,因為畫素是由基於整個影象的灰度分佈的變換函數修改的。當目的是為了解決增強影象中幾個小區域的細節時,解決方法是設計基於畫素鄰域的灰度分佈的變換函數。
區域性直方圖的處理過程:
- 定義一個鄰域,並將其中心在水平方向或垂直方向上從一個畫素移動到另一個畫素。
- 在每個位置,計算鄰域中的各點的直方圖,得到直方圖均衡化或直方圖規定化變換函數,將這個函數對映於鄰域中心點畫素的灰度。
- 然後將鄰域的中心移到一個相鄰畫素位置,並重覆上述過程。
區域性直方圖均衡化效果如下圖所示:

3.3.4,使用直方圖統計增強影象
直接從影象直方圖得到的統計量資訊可用於增強影象。令\(r\)是一個離散型隨機變數,它表示區間\([0,L-1]\)內的灰度值;令\(p(r_i)\)是相對於灰度值\(r_i\)的歸一化直方圖分量。即\(p(r_i)\)可視為灰度\(r_i\)的概率密度函數,並可得到影象的直方圖。
1,均值是平均灰度的測度,影象畫素灰度的均值\(m\)計算公式如下:
2,方差(或標準差\(\sigma\))是影象對比度的測度,方差公式如下:
簡單理解影象灰度均值和方差的意義就是,均值越大,影象越亮;方差越大,影象對比度越高。
上述公式是針對影象全域性的,其同樣可應用於一個規定大小的鄰域空間。結合以上公式和概念可以使用直方圖統計增強區域性影象,範例如下:

令\(f(x,y)\)表示原圖在影象座標\((x,y)\)處的灰度值,令\(g(x,y)\)表示增強後的影象在這些座標處的灰度值,具體的影象增強公式如下:

更詳細的具體操作方法細節參考原書,本文略過。
3.4,空間濾波基礎
本節內容討論如何使用空間濾波器進行影象處理。濾波有時要分多個階段完成。
濾波器一詞來自頻率域處理(第四章),濾波的意思是指通過修改或抑制影象的規定分量。例如,通過低頻的濾波器稱為低通濾波器。低通濾波器的作用是通過模糊影象來平滑影象,使用空間濾波器可以直接對影象本身進行類似效果的平滑處理。
3.4.1,線性空間濾波的原理
線性空間濾波定義: 指影象\(f\)與濾波器核\(w\)進行乘積之和(卷機)運算。核是一個陣列,其大小定義了運算的鄰域,其係數決定了該濾波器(也稱模板、視窗濾波器)的性質。
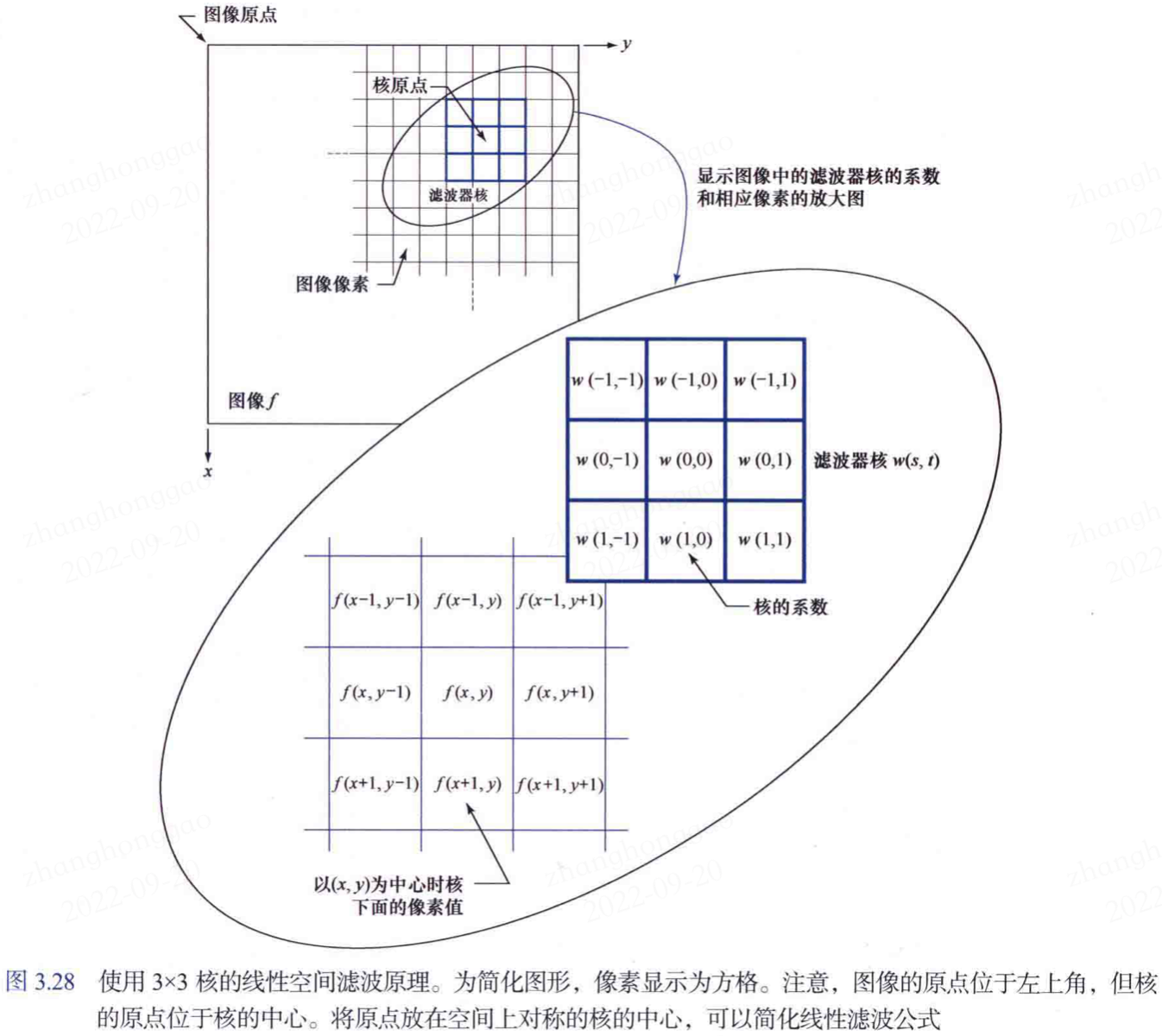
下圖3.28說明了使用\(3\times3\)核進行線性空間濾波的原理。在影象任何一點\((x,y)\)處,濾波器的響應\(g(x,y)\)是核係數核核所覆蓋影象畫素的乘積之和:
核的中心繫數值 \(w(0,0)\) 對應於 \((x,y)\) 處的畫素。對應大小為 \(m\times n\) 的核,假設 \(m=2a+1\) 和 \(n=2b+1\),其中\(a\)和\(b\)是非負整數。一般來說,大小為 \(m\times n\) 的核對大小為 \(M\times N\) 的影象的線性空間濾波可表示為:
上式中 \(x\) 和 \(y\) 發生變化,使得濾波器核的中心(原點)能夠遍歷完影象 \(f\) 中的每個畫素。
3.4.2,空間相關與折積
圖3.28以圖形方式說明了空間相關,式(3.31)給出了其數學描述。相關的運算過程如下:在影象上移動核中心,並且在每個位置計算乘積之和。
以一維例子開始,則式(3.31)變為
式中,卷機核為\(w\),影象函數為\(f\)。

在本書中,當我們使用線性空間濾波這個術語時,指的是濾波器核與影象進行卷機(乘積和)運算。
3.5,平滑(低通)空間濾波器
平滑(也稱平均)空間濾波器用於降低灰度的急劇過渡,因為隨機噪聲通常就是由灰度的急劇過渡組成,所以平滑的一個明顯應用就是降噪。
本節介紹基於可分離盒式核和高斯核的低通濾波器。
1,基於可分離盒式核的低通濾波器
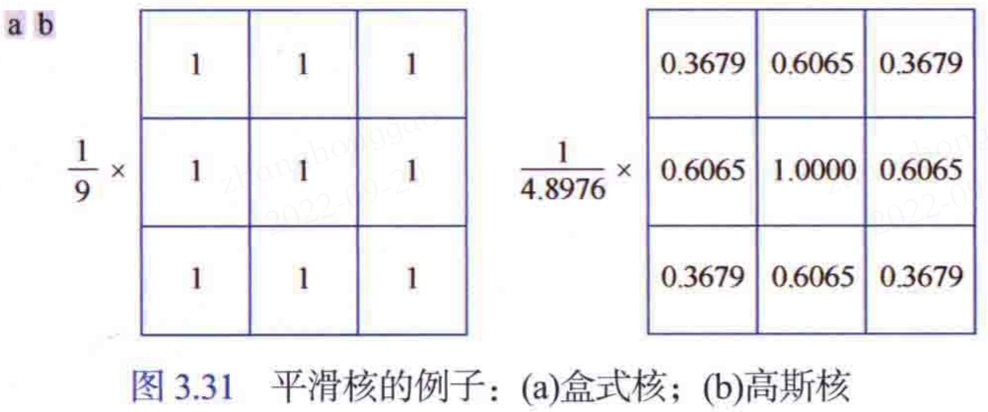
最簡單的可分離低通濾波器核是盒式核,其係數的值相同(通常為1)。
下圖3.31(a)中顯示了一個大小為\(3\times 3\)的盒式濾波器,即一個大小為\(m\times n\)的盒式濾波器且元素值為 1 的一個\(m\times n\)陣列,器前面有一個歸一化的常數,它的值是 1 除以係數值之和(當所有係數都為1時,這個常數為\(1/mn\))。
使用不同盒式核對影象進行低通濾波的效果圖如下所示:

盒式濾波器較為簡單,適合快速實驗,其會產生視覺上能夠接受的平滑效果。盒式濾波器有一些侷限:
- 對透鏡模糊特性的近視能力較差。
- 盒式濾波器往往沿垂直方向模糊影象,不適合精細細節或具有強幾何分量的影象應用。
對應的 opencv 函數如下。
void boxFilter( InputArray f, OutputArray dst, int ddepth,
Size ksize, Point anchor=Point(-1,-1),
bool normalize=true,
int borderType=BORDER_DEFAULT );
引數 6 的解釋:
- 當
normalize = true時,盒式濾波就變成了均值濾波。也就是說,均值濾波是盒式濾波歸一化(normalized)後的特殊情況。其中,歸一化就是把要處理的量都縮放到一個範圍內,比如(0,1),以便統一處理和直觀量化。 - 當
normalize = false時,為非歸一化的盒式濾波,用於計算每個畫素鄰域內的積分特性,比如密集光流演演算法(dense optical flow algorithms)中用到的影象倒數的協方差矩陣(covariance matrices of image derivatives)。
均值濾波,是最簡單的一種線性濾波操作,輸出影象的每一個畫素是核視窗內輸入影象對應畫素的畫素的平均值( 所有畫素加權係數相等),實質就是歸一化後的方框濾波。均值濾波演演算法比較簡單,計算速度快,但是均值濾波本身存在著固有的缺陷,即它不能很好地保護影象細節,在影象去噪的同時,也破壞了影象的細節部分,從而使影象變得模糊,不能很好地去除噪聲點。但均值濾波對週期性的干擾噪聲有很好的抑制作用。
3.5.2,低通高斯濾波器核
實際應用中要求折積核是各向同性的(圓對稱),其響應與方向無關。高斯核是唯一可分離的圓對稱核,因此非常適合影象處理,對於抑制服從正態分佈的噪聲非常有效。高斯核定義:
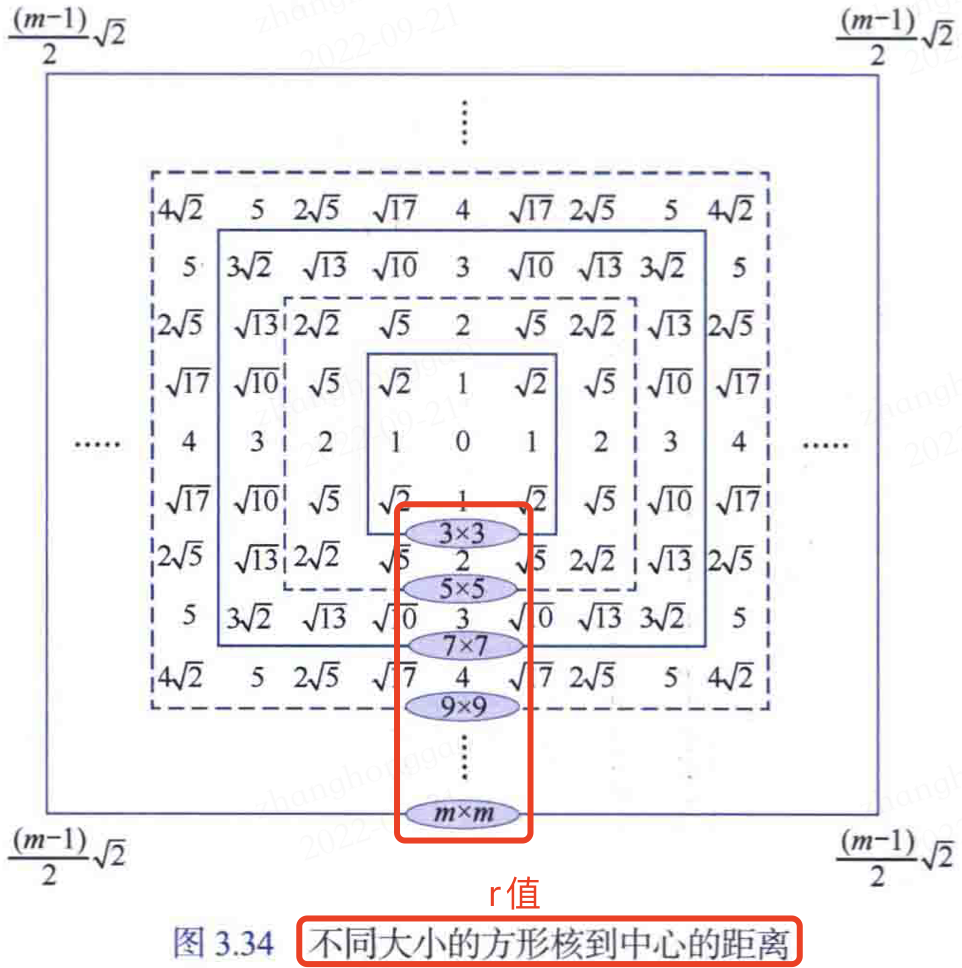
令\(r=[s^2+t^2]^{1/2}\),上式可寫為
這個函數依然是圓對稱的,變數\(r\)表示從中心到函數\(G\)上任意一點的距離,它必須是正數且是奇數。下圖顯示了不同大小的核的\(r\)值。
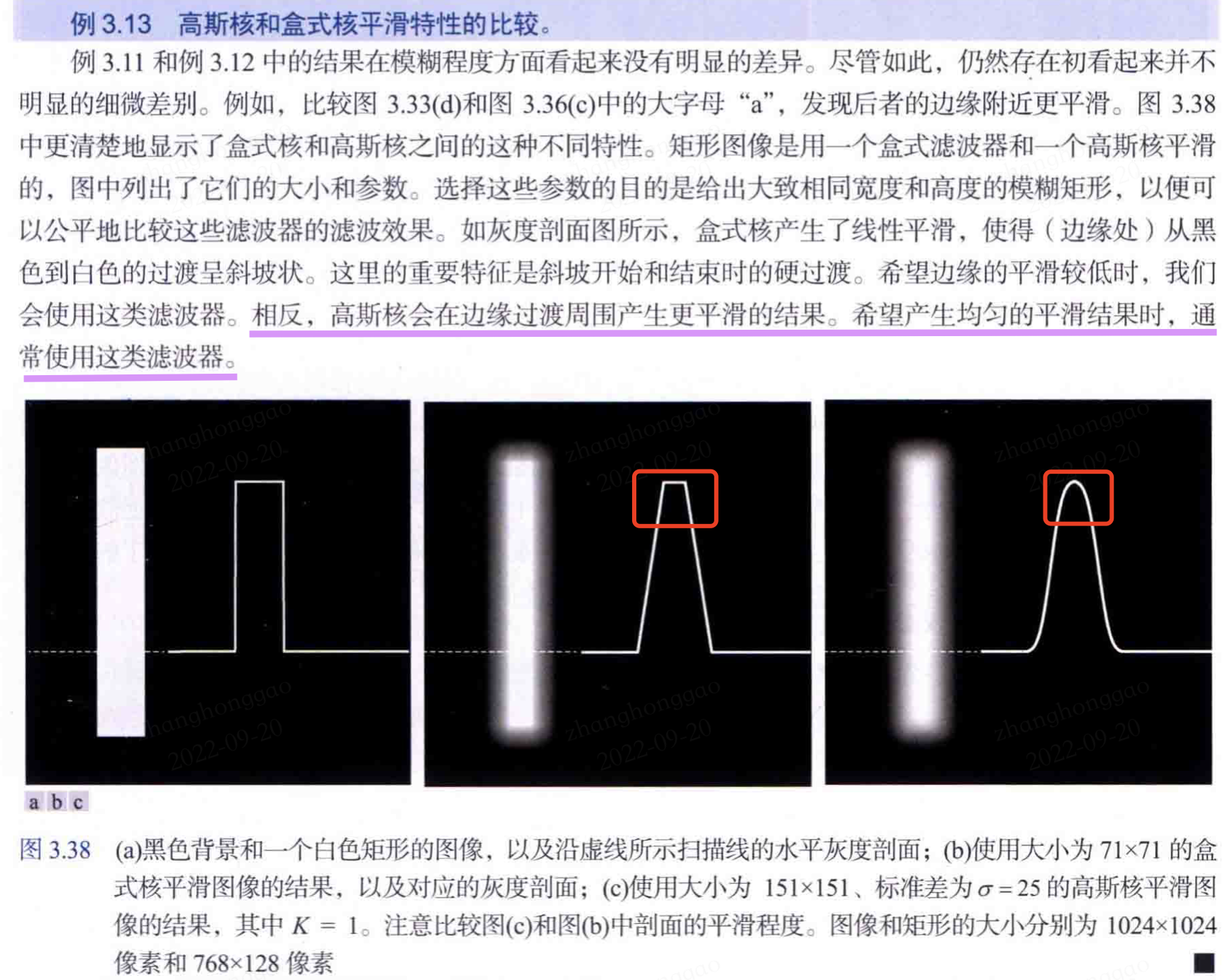
希望產生更均勻的平滑結果時,通常使用高斯核平滑;盒式核平滑則是硬過渡。
高斯核和盒式核平滑特性的比較對比圖如下:
3.5.3,低通濾波程式碼範例
盒式濾波、均值濾波(歸一化後的盒式濾波)、高斯濾波的 python-opencv 應用程式碼如下。
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('test.png')
blur1 = cv.boxFilter(img, -1 ,(3,3),normalize = False)
blur2 = cv.boxFilter(img, -1 ,(3,3),normalize = True)
blur3 = cv.GaussianBlur(img,(5,5),0)
plt.figure(figsize=(20,20)) #設定視窗大小
plt.subplot(221),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(blur1),plt.title('boxFilter_normalize_false')
plt.xticks([]), plt.yticks([])
plt.subplot(223),plt.imshow(blur2),plt.title('boxFilter_normalize_true')
plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(blur3),plt.title('Gaussian')
plt.xticks([]), plt.yticks([])
plt.show()
程式執行後輸出如下:
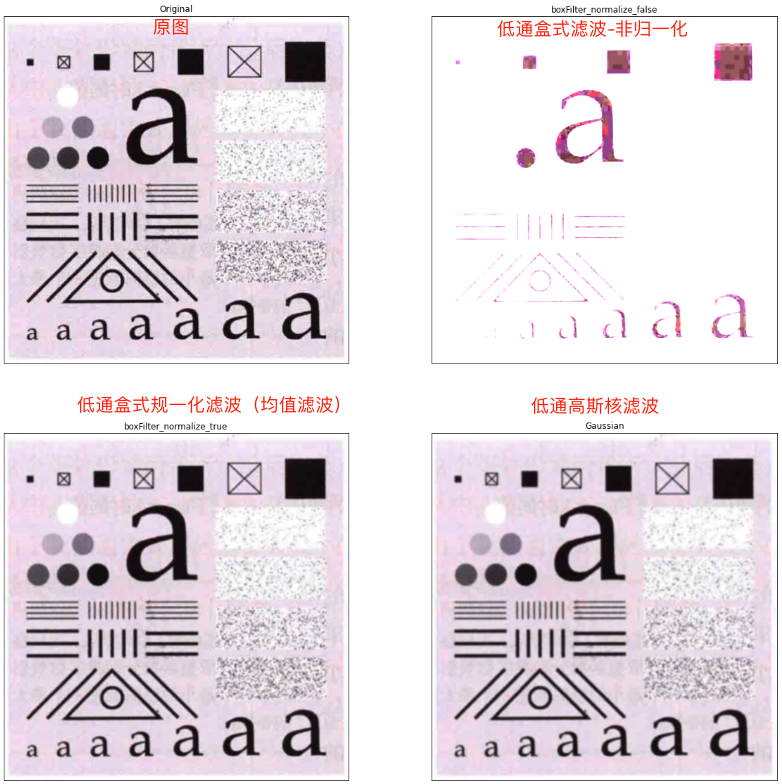
非歸一化的時候,得到影象就是一片白色,對源影象毀壞太大,根本無法使用。而歸一化的時候,得到影象是一種模糊的效果,此時與均值濾波一樣。
3.6,銳化(高通)空間濾波器
銳化的作用是突出灰度中的過渡。前面講的平滑(低通)濾波(影象模糊)通過積分運算實現的,那可以推斷出影象銳化可以用微分實現。
3.6.1,基礎
導數(英語:derivative)是微積分學中的一個概念。函數在某一點的導數是指這個函數在這一點附近的變化率。導數的本質是通過極限的概念對函數進行區域性的線性逼近。當函數\(f\)的自變數在一點 \(x_{0}\) 上產生一個增量 \(h\) 時,函數輸出值的增量與自變數增量 \(h\) 的比值在 \(h\) 趨於 0 時的極限如果存在,即為 \(f\) 在 \(x_{0}\) 處的導數,記作 \(f'(x_{0})\) 或 \(\frac{\mathrm{d} f}{\mathrm{d} x}x_0\) 或 \(\frac{\mathrm{d} f}{\mathrm{d} x}\mid_{x=x_0}\)。例如在運動學中,物體的位移對於時間的導數就是物體的瞬時速度。
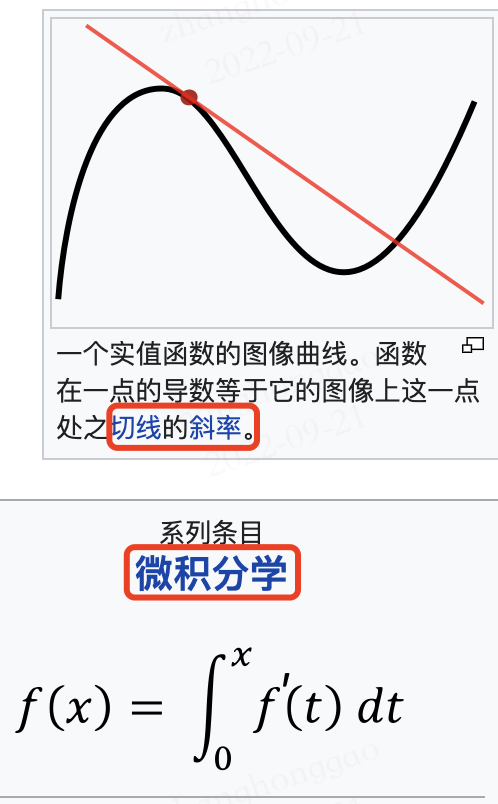
導數是函數的區域性性質。不是所有的函數都有導數,一個函數也不一定在所有的點上都有導數。若某函數在某一點導數存在,則稱其在這一點可導(可微分),否則稱為不可導(不可微分)。如果函數的自變數和取值都是實數的話,那麼函數在某一點的導數就是該函數所代表的曲線在這一點上的切線斜率。
導數一般定義如下:
直觀上 \(f(x)-f(a)\) 代表函數值從\(a\)到\(x\)的變化量,那麼,
代表的是從 \(a\) 到 \(x\) 的平均變化率。若實函數\(f\)於實數\(a\)有定義,且以下極限:
存在則稱 \(f\) 在 \(a\) 處可導。
來源維基百科導數定義。
一維函數\(f(x)\)的一階導數的一個基本定義是差分:
同理可將\(f(x)\)的二階導數定義為差分:
3.6.2,使用二階導數銳化影象-拉普拉斯
使用二階導數銳化影象的方法:首先定義二階導數的離散公式,然後在這個公式的基礎上構造一個濾波器核。對於兩個變數的函數(影象\(f(x,y)\))其中拉普拉斯運算元(核)的定義如下:
因為任意階的導數都是線性運算元,所以拉普拉斯是線性運算元。
由差分和拉普拉斯二階導數的定義可得如下公式:
上述公式可以用圖3.45(a)中的核進行折積運算來實現;因此,影象銳化的濾波原理類似於3.5節內容所述的低通濾波,只是這裡使用不同的核係數。
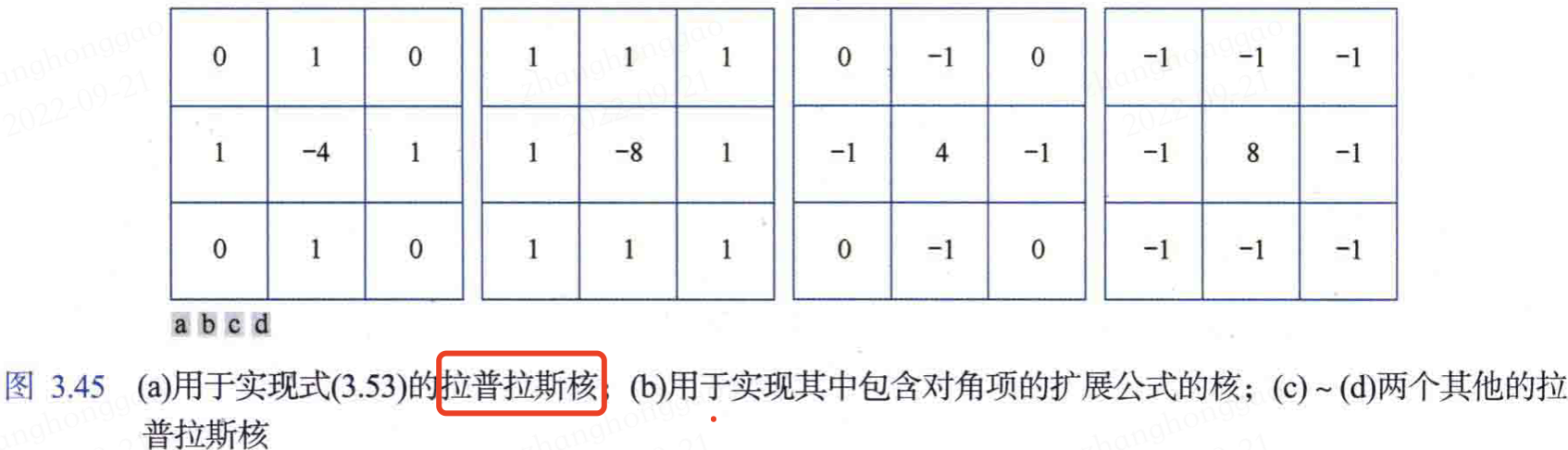
使用拉普拉斯運算元銳化影象的方法描述如下:

直接的拉普拉斯影象往往是黑色和無特徵的。
拉普拉斯應用範例如下:
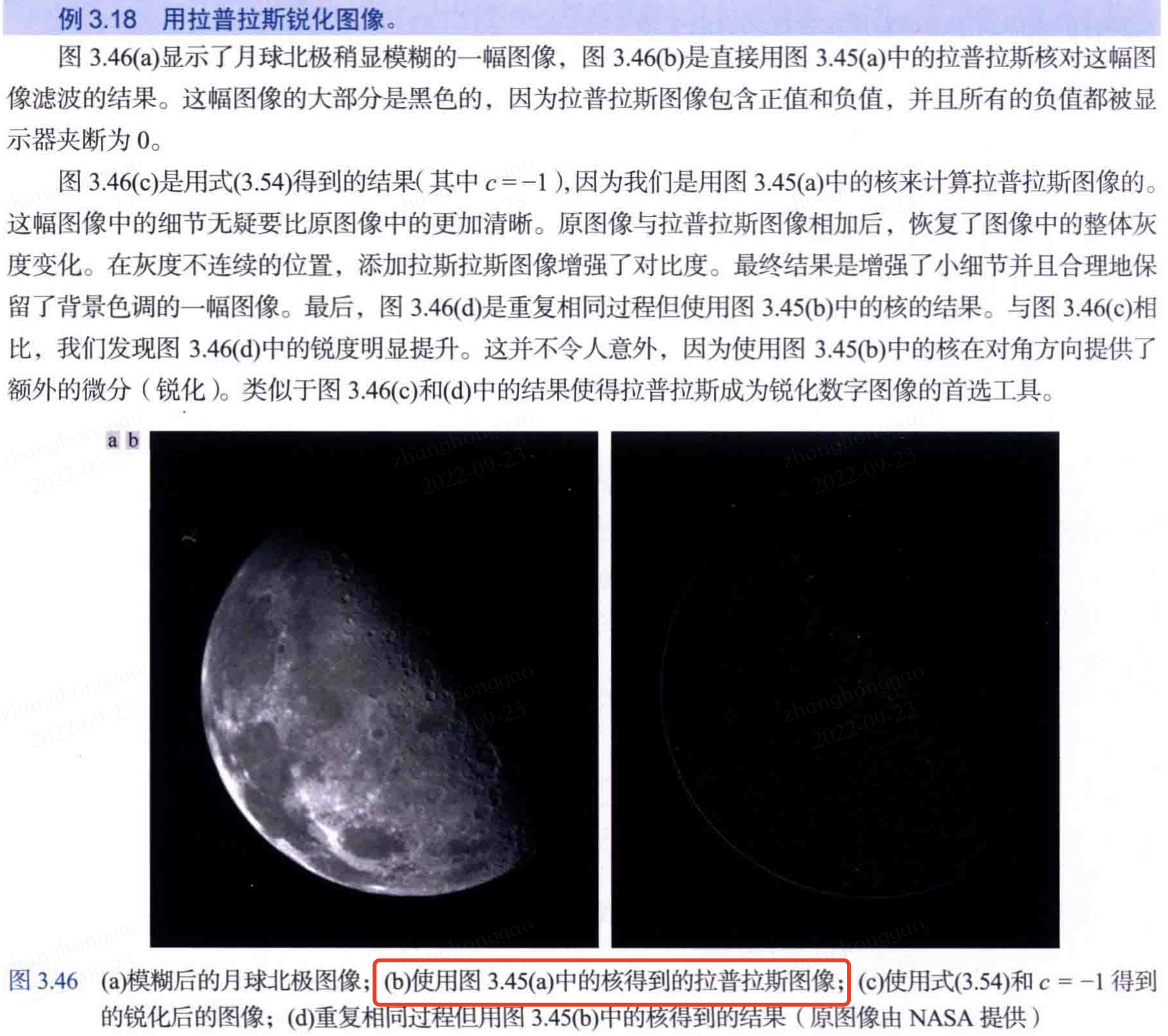
3.6.3,鈍化掩蔽和高提升濾波
從原影象減去一幅鈍化(平滑後)影象,是20世紀30年代以來印刷和出版業一直用來銳化影象的方法,這個過程稱為鈍化掩蔽,步驟如下:
- 模糊原影象。
- 從原影象減去模糊後的影象(產生的差稱為模板)。
- 將模板與原影象相加。

注意較大的 k 值會產生令人無法接受的影象。
鈍化掩蔽效果範例:

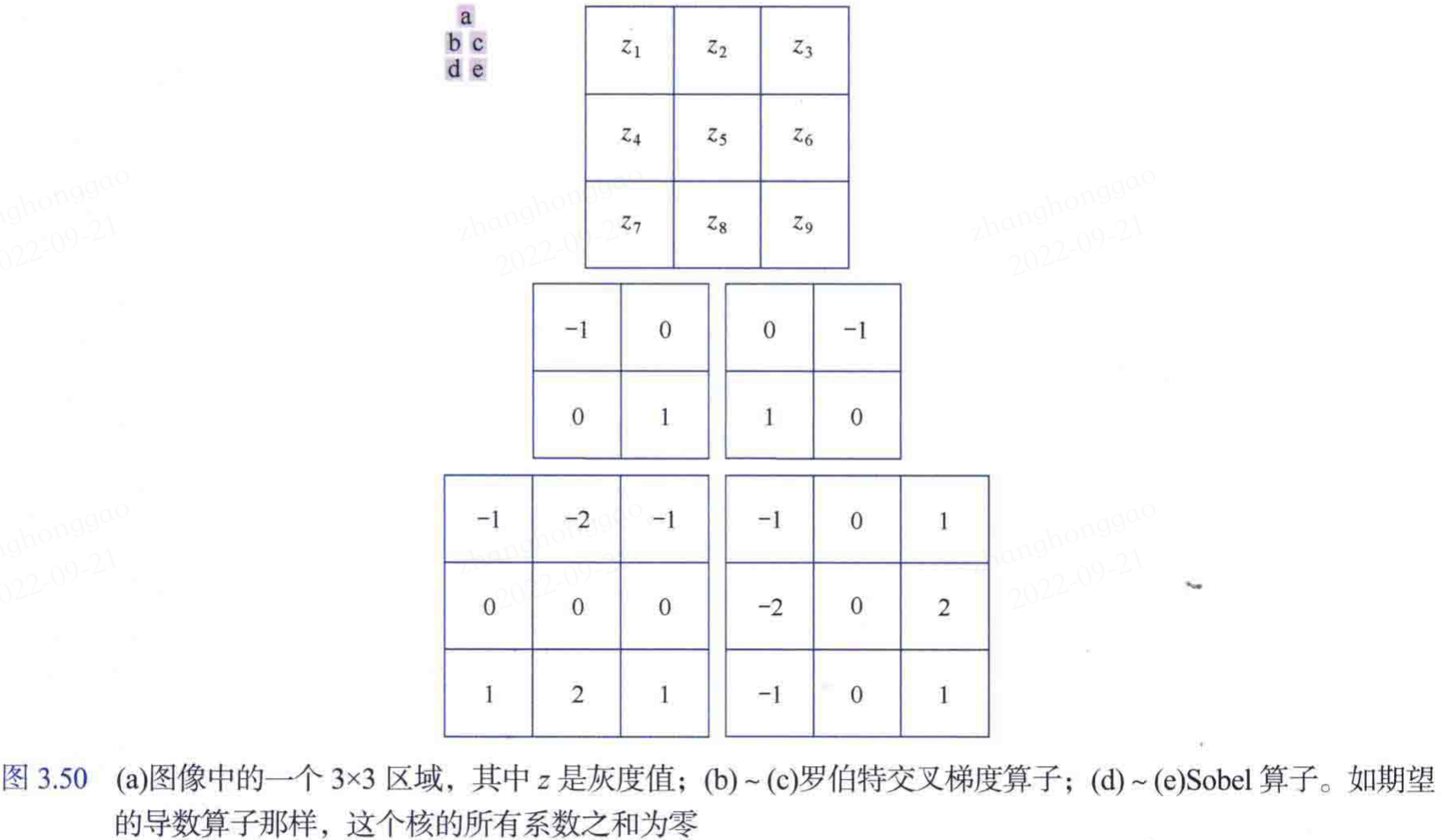
3.6.4,使用一階導數銳化影象-梯度
包括羅伯特交叉梯度運算元和 Sobel 運算元,使用一階梯度運算元銳化影象常用在工業缺陷檢測。梯度運算元核係數矩陣如下:
3.7,低通、高通、帶阻核帶通濾波器
3.8,組合使用空間增強方法
使用拉普拉斯來突出細節,使用梯度來增強突出的邊緣。
四,頻率域濾波
4.1,背景
- 傅立葉級數: 任何周期函數都可表示為不同頻率的正弦函數和/或餘弦函數之和,其中每個正線函數和/或餘弦函數都乘以不同的係數(我們現在稱該和為傅立葉級數)。
- 傅立葉變換: 任何非周期函數都可表示為正弦函數和/或餘弦函數乘以加權函數的積分。
略。
4.2,基本概念
- 複數
- 傅立葉級數
- 衝激函數及其取樣(篩選)性質
- 連續單變數函數的傅立葉變換
- 折積
4.3,取樣和取樣函數的傅立葉變換
略。
4.8,使用低通頻率域濾波器平滑影象
影象中的邊緣和其他急劇的灰度變化(如噪聲)主要影響其傅立葉變換的高頻內容,因此,在頻率域中是通過衰減高頻(即低通濾波)來實現平滑(模糊)的。
五,影象復原與重建
影象增強主要是一種主觀處理,而影象復原很大程度上是一種客觀處理技術。
六,彩色影象處理
6.1,彩色基礎
光的特性是色彩科學的核心,如果光是無色(無顏色)的,那麼其屬性就只有亮度或數值,具體體現就是20世紀20年度的黑白電影。其中術語灰度(或亮度)級是關於(從黑色變為灰色最終變為白色)灰度的一個測量,是一個標量。
彩色光在電磁波譜中的波長範圍是 400~700nm,描述光源質量的 3 個基本量是輻射亮度、發光強度和亮度。人眼的生理結構特性表現為其對紅色、綠色和藍色光更為敏感,該特性使得人眼看到的顏色是三原色 [紅 R、綠 G、藍 B] 的不同組合。三原色相加可以產生光的二次色,如深紅色(R+B)、青色(G+B)和黃色(R+G)。
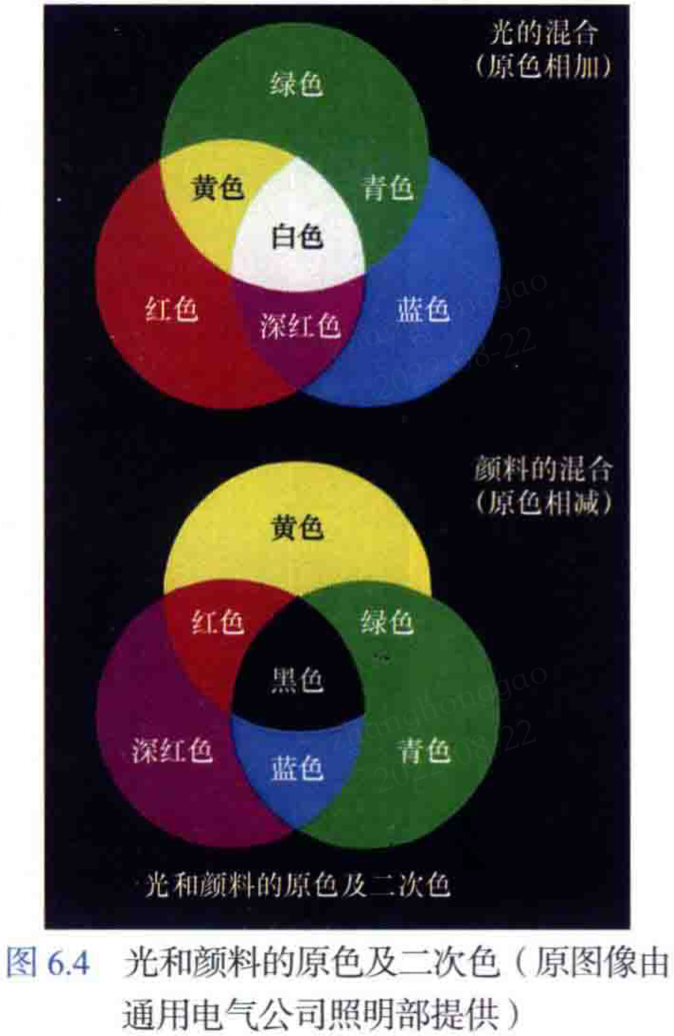
區分不同顏色的特性通常是亮度、色調和飽和度,色調與飽和度一起稱為色度。
- 亮度:亮度體現的是發光強度(灰度級)的消色概念。
- 色調:色調是混合光波中與主導波長相關的屬性,表示被觀察者感知的主導色。即,當我們說一個物體顏色說紅色、橙色或紅色時,說的就是物體的色調。
- 飽和度:飽和度指的是相對的純度(純色被白光稀釋的程度),或與一種色調混合的白光量。純光譜顏色是完全飽和的,非光譜顏色如淡紫色(紫色加白色)是不飽和度,飽和度與所加白光量成反比。
6.2,彩色模型
彩色模型(也稱彩色空間或彩色系統)的目的是以某種標準的方式來方便地規定顏色。彩色模型本質上規定:(1)座標系;(2)座標系內的字空間,模型內的每種顏色都可由字空間內包含的一個點來表示。數位影像處理中的面向硬體的彩色模型常用有以下幾種:
- 針對彩色顯示器和彩色攝像機開發的
RGB(紅色、綠色、藍色)模型。 - 針對彩色印表機開發的
CMY(青色、深紅色、黃色)模型和CMYK(青色、深紅色、黃色、黑色)模型。 - 針對人們描述和解釋顏色的方式開發的
HSI(色調、飽和度、亮度)模型。HSI模型有一個優點:它能夠解除影象中顏色和灰度級資訊的聯絡。
6.2.1,RGB 彩色模型
在 RGB 模型中,每種顏色都以其紅色、綠色和藍色光譜成分顯示,該模型是根據笛卡爾座標系建立的。RGB 彩色立方體簡圖如下所示:
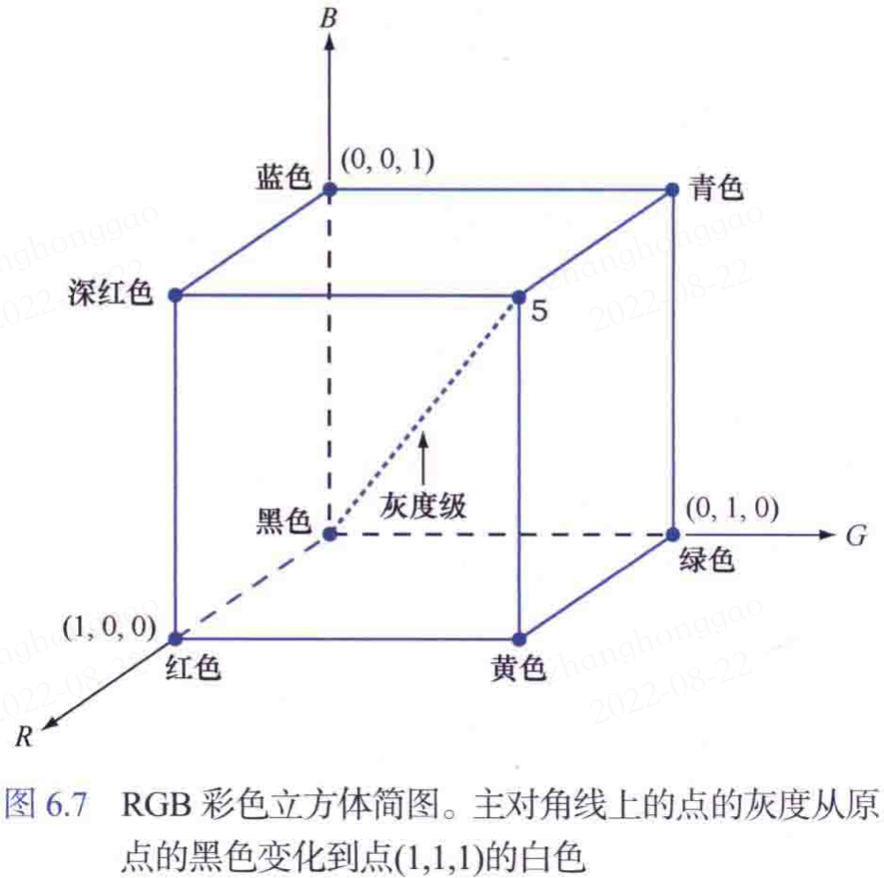
全綵色影象通常是指一幅 24 位元的 RGB 彩色影象(每幅分量影象都是 8 位,值域是 [0, 255]),顏色總數自然是 \((2^8)^3\)=16777216。
6.2.2,HSI 彩色模型
RGB 、CMY 和 CMYK 模型適合硬體實現但是並不能很好的描述人類世紀解釋的顏色;觀察彩色物體時,我們會用色調、飽和度和亮度來描述這個物體,由此提出了 HSI 彩色模型(色調、飽和度、亮度)。
從 RGB 到 HSI 的彩色變換的公式如下:

6.4,全綵色影象處理基礎
全綵色影象處理方法主要分為兩種。第一種方法是首先分佈處理每幅灰度級分量影象,然後將處理後的各幅分量影象合成為一幅彩色影象。第二種方法是直接處理彩色畫素。因為全綵色影象至少有 3 個分量,因此彩色畫素是向量。全綵色影象的公式定義如下:

6.5,彩色變換
本節中描述的技術是在單個彩色模型中處理彩色影象的各個分量,而不是像6.2節中那樣在彩色模型之間進行彩色變換。
6.5.1,公式
使用如下公式對多光譜影象的顏色變換建模:
式中,\(n\)是分量影象的總數,\(r_i\)是輸入分量影象的灰度值,\(s_i\)是輸出分量影象中空間上的對應灰度,\(T_i\)是對\(r_i\)操作來產生\(s_i\)的一組變換或顏色對映函數。
6.5.4,色調和彩色校正
只有校正了影象的色調範圍,才能解決影象中顏色的不規則問題,如過飽和顏色和欠飽和顏色問題。影象中的色調範圍(也稱主特性),是指影象中顏色亮度的一般分佈。高主特性影象中的大部分資訊集中在高亮度上;低主特性影象中的大部分資訊集中在低亮度上;中主特性影象的顏色則介於前兩者之間。我們通常希望彩色影象的亮度在高光和陰影之間是等間隔分佈的。

彩色平衡。影象的色調特性完成之後,通常要解決彩色不平衡的問題。校正彩色不平衡的方法有很多種,調整一度彩色影象的彩色分量時,要意識到每個操作都會影響影象的整體彩色平衡。也就是說,對一種顏色的感知會受到周圍顏色的影響。
6.5.5,彩色影象的直方圖處理
和前一節內容是互動式增強方法(手動調節感知合適與否)不同,3.3 節的灰度直方圖處理變換可自動地應用於彩色影象。
直方圖均衡化會通過一個變換函數,輸出一幅具有均勻灰度值直方圖的影象。
HSI 彩色空間更適合均勻地分佈顏色亮度,同時保持顏色本身(即色調)不變。

6.6,彩色影象平滑和銳化
彩色變換是變換影象中的每個畫素而不考慮畫素的鄰域,那麼下一步自然是根據周圍畫素(鄰域)的特性來修改畫素的值。本節內容通過彩色影象的平滑和銳化處理來說明這類鄰域處理的基本知識。
6.6.1,彩色影象的平滑
灰度級影象的平滑(空間濾波)概念同樣可適用於全綵色影象處理,只是我們處理的不再是標量灰度值,而是式(6.37)給出的分量向量。彩色影象平滑公式描述如下:

6.6.2,彩色影象的銳化
向量分析表明,一個向量的拉普拉斯也是一個向量,其分量等於輸入向量的各個標量分量的拉普拉斯。在 RGB 彩色系統中,式(6.37)中向量\(c\)的拉普拉斯為
上式(6.37)表明分別計算每幅影象的拉普拉斯,即可求出全綵色影象的拉普拉斯。使用拉普拉斯銳化彩色影象範例如下:

八,影象壓縮和水印
影象壓縮是一種減少表示一幅影象所需資料量的技術與課業。本章內容是介紹性的,適用於影象和視訊應用。
8.1,基礎
二維灰度矩陣是我們檢視和解釋影象的首選格式,並且是評判其他表示的標準。二維灰度陣列受如下能被識別和利用的三種主要資料冗餘的影響:
- 編碼冗餘。
- 空間和時間冗餘。
- 無關資訊。
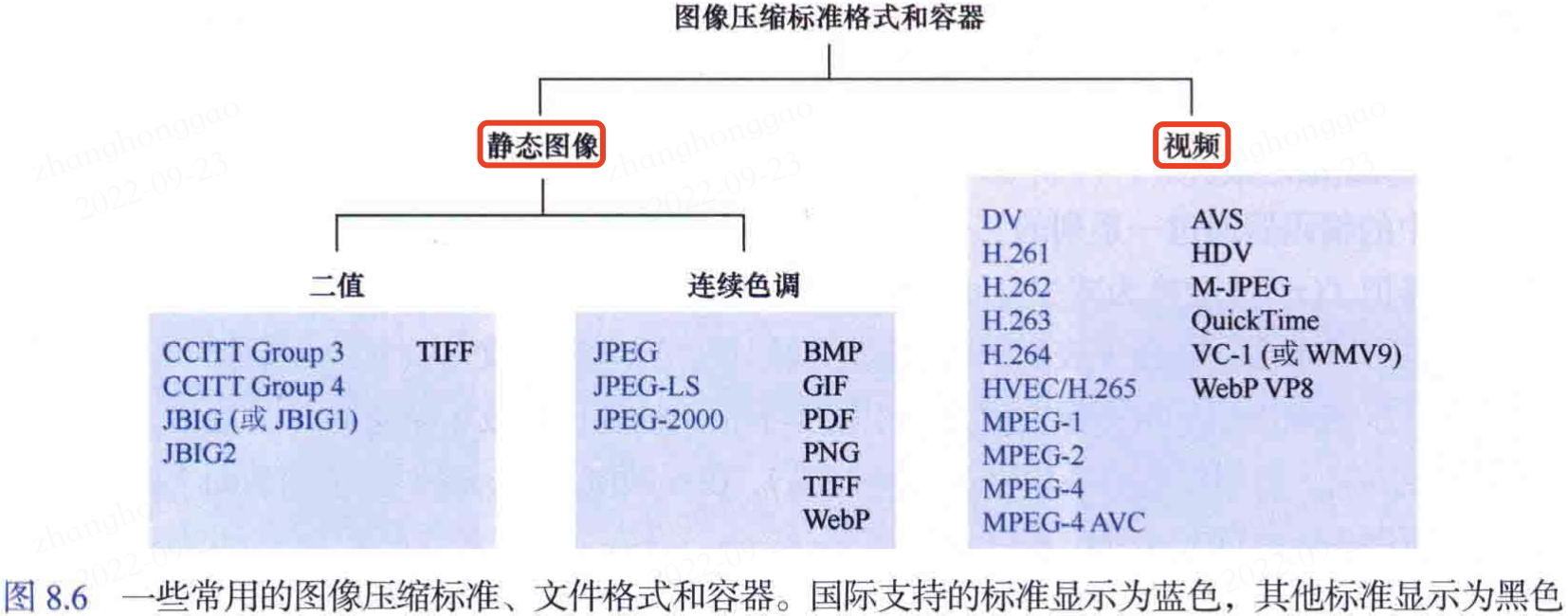
8.1.7,影象格式、記憶體(容器)和壓縮標準
在數位影像處理環境中,影象檔案格式是組織和儲存影象資料的標準方法,它定義了資料的排列方式和所用的壓縮型別。一些常用的影象壓縮標準、檔案格式和容器如下圖所示:
8.2,霍夫曼編碼
霍夫曼提出了消除編碼冗餘的一種常用技術。
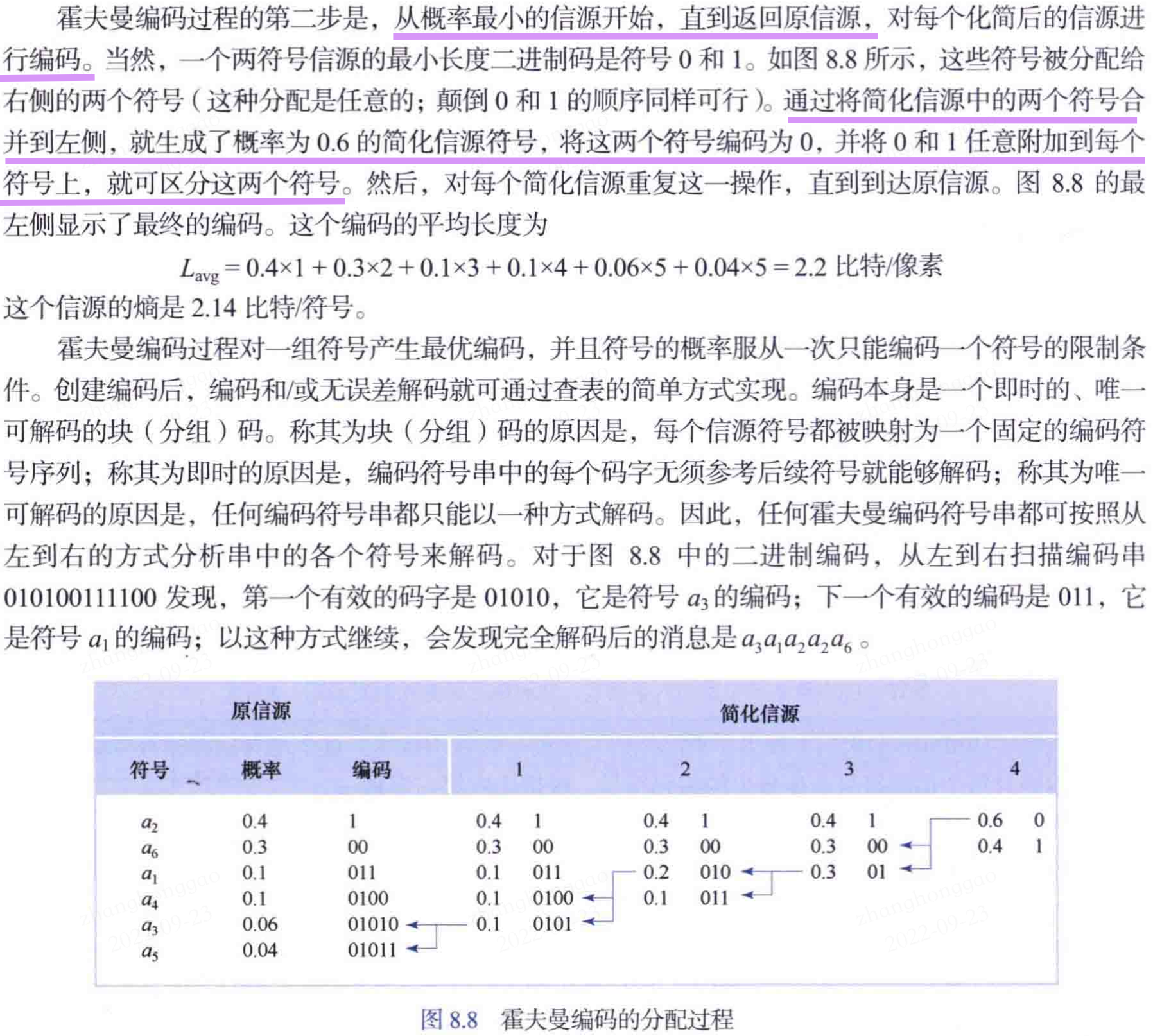
1,霍夫曼編碼過程第1步如下:


2,霍夫曼編碼過程第2步如下:
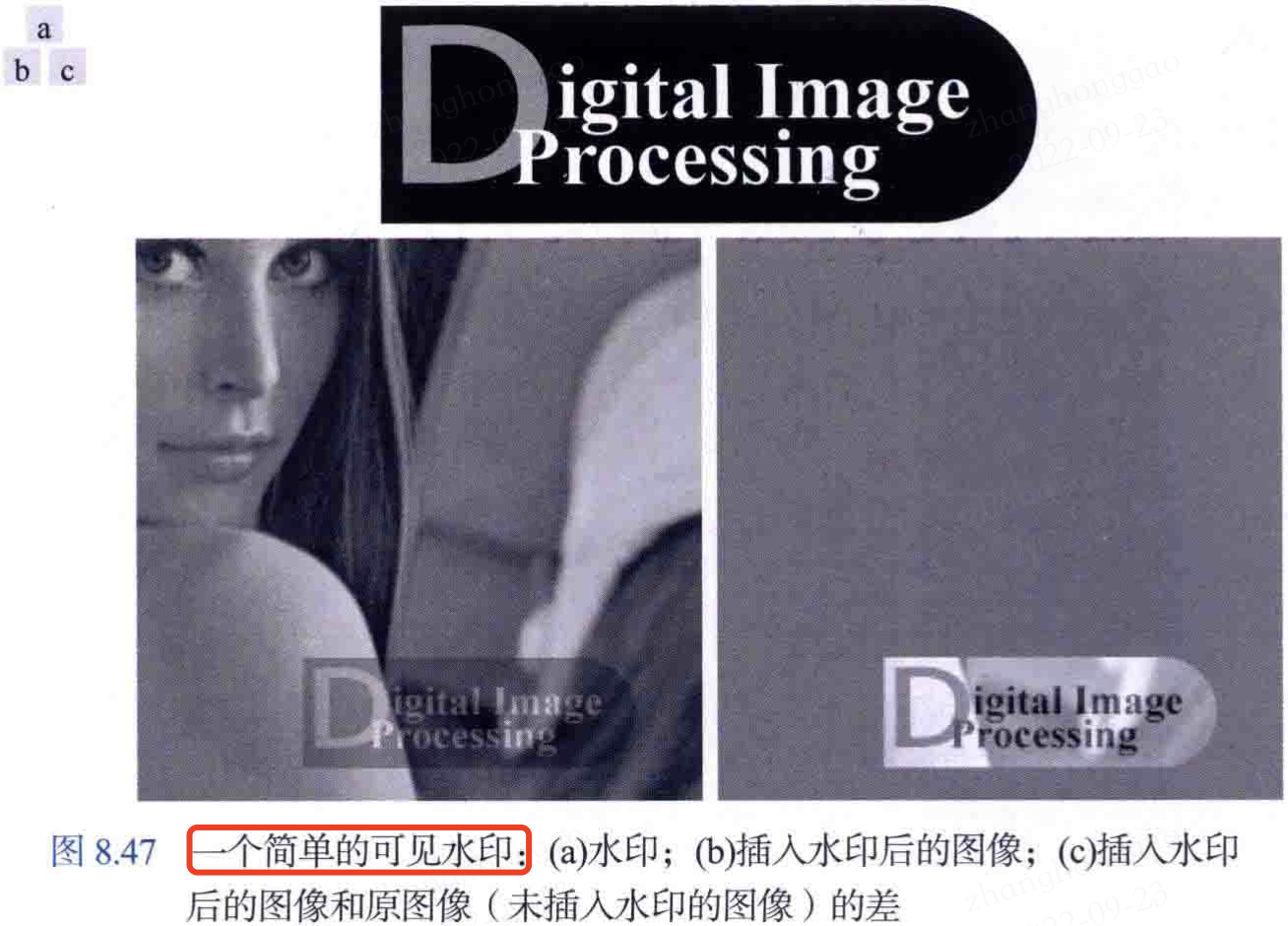
8.12,數位影像水印
簡單的可見水印定義: 若令 \(f_w\) 表示新增了水印的影象,則可將它表示為未加水印影象\(f\)和水印\(w\)的線性組合:
式中,常數\(\alpha\)控制水印和底層影象的相對可見度。一個簡單的可見水印範例圖如下:
參考資料
《數位影像處理第四版》