論文資訊

論文標題：MixMatch: A Holistic Approach to Semi-Supervised Learning
論文作者：David Berthelot, Nicholas Carlini, Ian Goodfellow, Nicolas Papernot, Avital Oliver, Colin Raffel
論文來源：NeurIPS 2019
論文地址：download 
論文程式碼：download
參照次數：1898

1 Introduction

　　半監督學習[6]（SSL）試圖通過允許模型利用未標記資料，減輕對標記資料的需求。最近的半監督學習方法在未標記的資料上增加一個損失項，鼓勵模型推廣到不可見的資料。該損失項大致可分： 

• • 熵最小化（entropy minimization）[18,28]——鼓勵模型對未標記資料產生高質信度的預測；
  • 一致性正則化（consistency regularization）——鼓勵模型在輸入受到擾動時產生相同的輸出分佈；
  • 通用正則化（generic regularization）——鼓勵模型很好地泛化，避免過擬合；

2 Related Work

2.1 Consistency Regularization

　　監督學習中一種常見的正則化技術是資料增強，它被假定為使類語意不受影響的輸入轉換。例如，在影象分類中，通常會對輸入影象進行變形或新增噪聲，這在不改變其標籤的情況下改變影象的畫素內容。即：通過生成一個接近的、無限新的、修改過的資料流來人為地擴大訓練集的大小。

　　一致性正則化將資料增強用於半監督學習，基於利用一個分類器應該對一個未標記的例子輸出相同的類分佈的想法。正式地說，一致性正則化強制執行一個未標記的樣本 $x$ 應與 $\text{Augment(x)}$ 分類相同。

　　在最簡單的情況下，對於未標記的樣本 $x$，先前工作[25,40]新增如下損失項：

　　　　$\| \mathrm{p}_{\text {model }}(y \mid \operatorname{Augment}(x) ; \theta)-\mathrm{p}_{\text {model }}(y \mid \text { Augment }(x) ; \theta) \|_{2}^{2}\quad\quad(1)$

　　注意，$\text{Augment(x)}$ 是一個隨機變換，所以 $\text{Eq.1}$ 中的兩項 $\text{Augment(x)}$ 是不完全相同的。

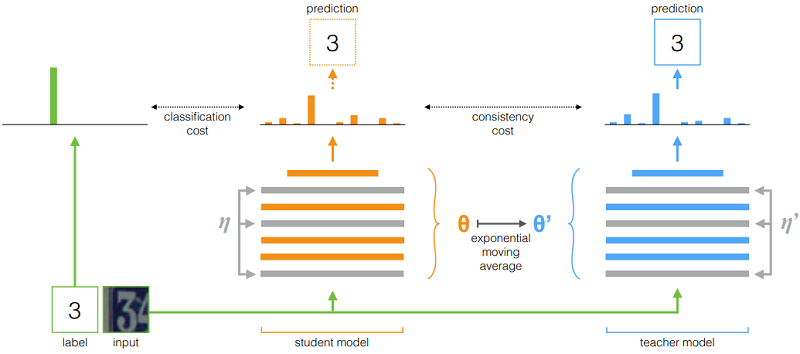
　　類似的操作 [44](基於模型引數擾動)：

　　　　$\begin{array}{l} J(\theta)=\mathbb{E}_{x, \eta^{\prime}, \eta}\left[\left\|f\left(x, \theta^{\prime}, \eta^{\prime}\right)-f(x, \theta, \eta)\right\|^{2}\right]\\\theta_{t}^{\prime}=\alpha \theta_{t-1}^{\prime}+(1-\alpha) \theta_{t}\end{array}$

　　圖示：

2.2 Entropy Minimization

　　許多半監督學習方法中，一個基本假設是：分類器的決策邊界不應該通過邊緣資料分佈的高密度區域。實現的一種方法是要求分類器對未標記的資料輸出低熵預測，[18]中其損失項使未標記資料 $x$ 的 $\operatorname{p}_{\text {model}}(y \mid x ; \theta)$ 的熵最小化。$\text{MixMatch}$ 通過對未標記資料的分佈使用 $\text{sharpening}$ 函數，隱式地實現了熵的最小化。

3 MixMatch 

　　給定一批具有 $\text{one-hot}$ 標籤的樣本集 $\mathcal{X}$ 和一個同等大小的未標記的樣本集 $U$，$\text{MixMatch}$ 生成一批經過處理的增強標記樣本 $\mathcal{X}^{\prime}$ 和一批帶「猜測」標籤的增強未標記樣本 $\mathcal{U}^{\prime}$，然後使用 $\mathcal{U}^{\prime}$ 和 $\mathcal{X}^{\prime}$ 計算損失項：

　　　　$\begin{array}{l}\mathcal{X}^{\prime}, \mathcal{U}^{\prime} & =&\operatorname{MixMatch}(\mathcal{X}, \mathcal{U}, T, K, \alpha) \quad \quad \quad\quad\quad(2)\\\mathcal{L}_{\mathcal{X}} & =&\frac{1}{\left|\mathcal{X}^{\prime}\right|} \sum\limits_{x, p \in \mathcal{X}^{\prime}} \mathrm{H}\left(p, \text { p }_{\text {model }}(y \mid x ; \theta)\right) \quad \quad\quad(3)\\\mathcal{L}_{\mathcal{U}} & =&\frac{1}{L\left|\mathcal{U}^{\prime}\right|} \sum\limits _{u, q \in \mathcal{U}^{\prime}}\|q-\operatorname{p}_{\text{model}}(y \mid u ; \theta)\|_{2}^{2} \quad \quad(4) \\\mathcal{L} & =&\mathcal{L}_{\mathcal{X}}+\lambda_{\mathcal{U}} \mathcal{L}_{\mathcal{U}}  \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(5)\end{array}$

　　其中，$\text{H(p, q)}$ 代表著交叉熵損失。

3.1 Data Augmentation

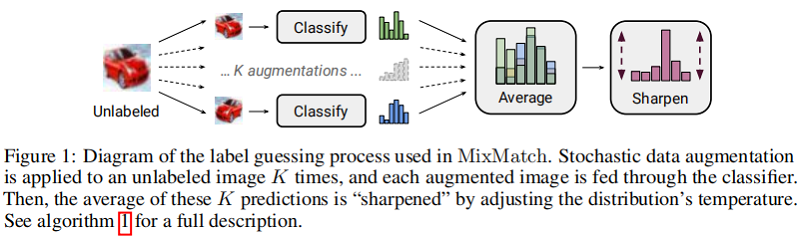
　　如許多 SSL 方法中的那樣，對標記和未標記資料使用資料增強。對於一批帶標記資料 $\mathcal{X}$ 中的每個 $x_{b}$ 生成一個資料增強樣本 $\hat{x}_{b}=\operatorname{Augment}\left(x_{b}\right)$；對未帶標記的資料集 $\mathcal{U}$ 中的樣本 $u_{b}$，生成 $K$ 個資料增強樣本 $\hat{u}_{b, k}=  \operatorname{Augment}  \left(u_{b}\right)$，$k \in(1, \ldots, K)$，下文為每個 $u_{b}$ 生成一個「猜測標籤」 $q_{b}$。

3.2 Label Guessing

　　對於 $\mathcal{U}$ 中的每個未標記的樣本，$\text{MixMatch}$ 使用模型預測為該樣本生成一個「猜測標籤」，通過計算模型對 $u_b$ 的預測類分佈的平均值：

　　　　$\bar{q}_{b}=\frac{1}{K} \sum\limits _{k=1}^{K} \operatorname{p}_{\text{model}}\left(y \mid \hat{u}_{b, k} ; \theta\right)\quad\quad(6)$

　　接著使用 銳化函數（$\text{Sharpen}$） 來調整這個分類分佈：

　　　　$\operatorname{Sharpen}(p, T)_{i}:=p_{i}^{\frac{1}{T}} / \sum\limits _{j=1}^{L} p_{j}^{\frac{1}{T}}\quad\quad(7)$

　　其中，$p$ 是輸入的類分佈，此處 $p= \bar{q}_{b}$；$T$ 是超引數，當 $T \rightarrow 0$ 時，$\text{Sharpen(p,T)}$ 的輸出接近 $\text{one-hot}$ 形式；

　　通過改小節內容為無標籤樣本 $u_{b}$ 產生預測分佈，使用較小的 $T$ 會鼓勵模型產生較低熵的預測。

3.3 MixUp

　　對於一個 Batch 中的樣本（包括無標籤資料和帶標籤資料），對於任意兩個樣本 $\left(x_{1}, p_{1}\right)$,$\left(x_{2}, p_{2}\right) $ 計算 $\left(x^{\prime}, p^{\prime}\right)$ ：

　　　　$\begin{aligned}\lambda & \sim \operatorname{Beta}(\alpha, \alpha)\quad \quad \quad \quad\quad(8)\\\lambda^{\prime} & =\max (\lambda, 1-\lambda)\quad \quad \quad\quad(9)\\x^{\prime} & =\lambda^{\prime} x_{1}+\left(1-\lambda^{\prime}\right) x_{2}  \quad\quad(10)\\p^{\prime} & =\lambda^{\prime} p_{1}+\left(1-\lambda^{\prime}\right) p_{2}  \quad\quad(11)\end{aligned}$

　　其中，$\alpha$ 是一個超引數。

　　鑑於已標記和未標記的樣本在同一批中，需要保留該$\text{Batch}$ 的順序，以適當地計算單個損失分量。通過 $\text{Eq.9}$ 確保 $x^{\prime}$ 更接近 $x_1$ 而不是 $x_2$。為了應用 $\text{MixUp}$，首先收集所有帶有標籤的增強標記範例和所有帶有猜測標籤的未標記範例：

　　　　$\begin{array}{l}\hat{\mathcal{X}}=\left(\left(\hat{x}_{b}, p_{b}\right) ; b \in(1, \ldots, B)\right)  \quad\quad(12)   \\\hat{\mathcal{U}}=\left(\left(\hat{u}_{b, k}, q_{b}\right) ; b \in(1, \ldots, B), k \in(1, \ldots, K)\right) \quad\quad(13)  \end{array}$

　　完整演演算法如下：

4 Experiment