技術文章 » 色彩學學習筆記

色彩學學習筆記

2023-01-07 18:01:55

色彩學學習筆記

可見光

可見光只佔電磁波譜的一小部分

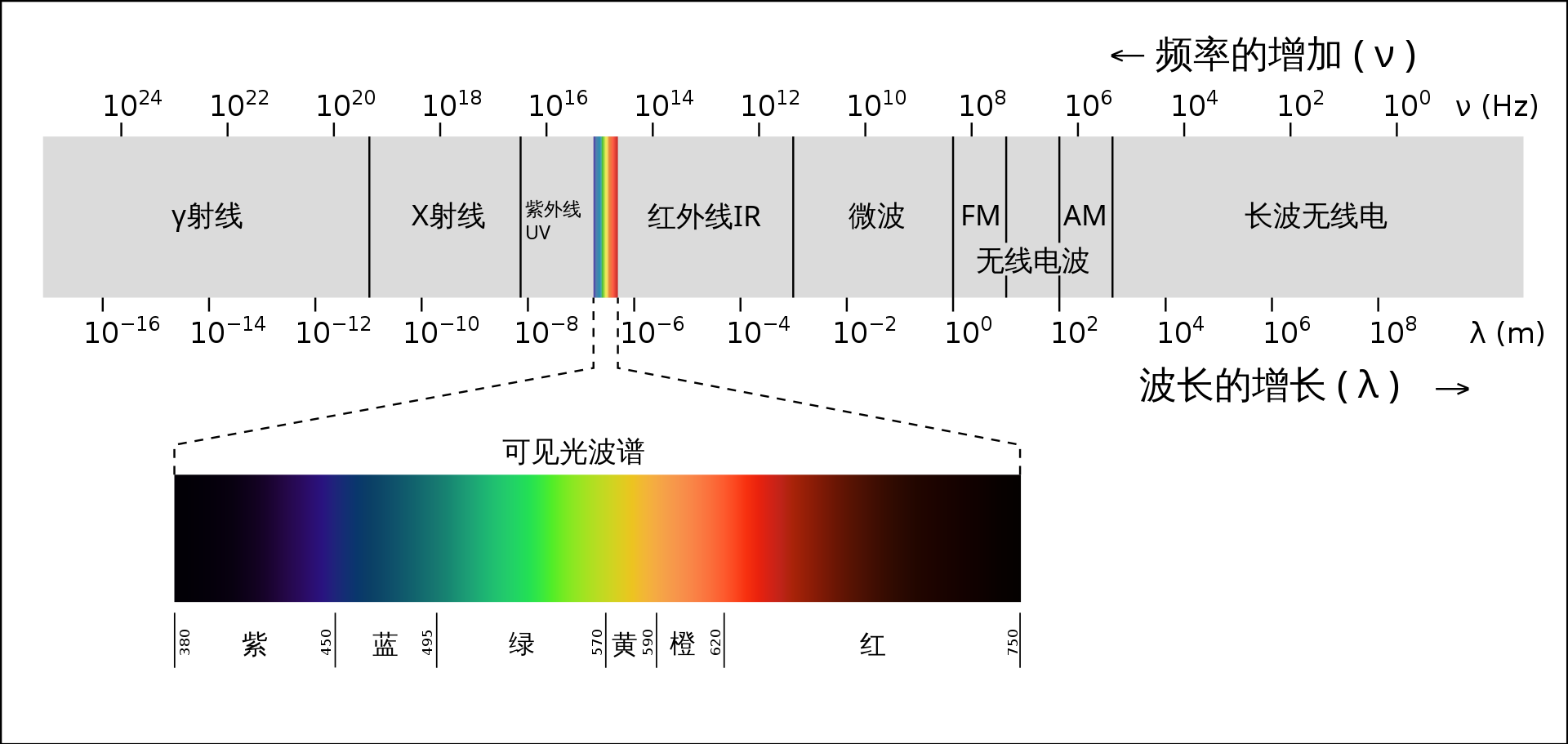
一個物體反射的光如果在所有可見光波長範圍內是平衡的，那麼對觀察者來說顯示為白色。然而，一個物體反射有限的可見光譜, 則物體呈現某種顏色

顏色的屬性

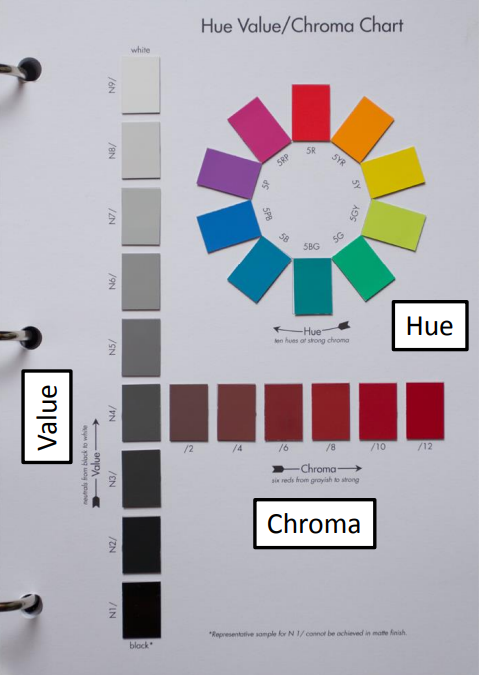
顏色有三種屬性

  • 色相/色調（Hue）
    • 顏色的主色調，如紅色、藍色
    • 由佔主要比例的波長決定
  • 亮度（Value/Lightness/Brightness）
    • 顏色的明暗程度
    • 無色光的屬性只有亮度
  • 色度/飽和度（Saturation/Chroma/Color Purity）
    • 顏色的純淨程度

色彩空間

CIE

為什麼需要 CIE 色彩空間？

  • 平時我們所說的 RGB 值實際上是裝置相關的，它沒規定用來混合的 R、G、B 究竟是什麼顏色，造成的結果是同樣的 RGB 值在不同裝置上會展示出不同的顏色
  • CIE 色彩空間是裝置獨立的，裝置可以將它們自己色彩空間裡的值對映到 CIE 色彩空間上，這樣就提供了規範的色彩空間，用來在不同裝置之間傳遞資訊

顏色匹配實驗

定義三原色，再通過顏色疊加以得到其他顏色，如果混合色和待測色達成一致，那麼三原色的分量被稱為待測色的三色刺激值

CIE RGB

CIE 規定了紅綠藍三原色光為標準波長為 700 nm（紅色）、546.1 nm（綠色）和 435.8 nm（藍色），再通過顏色匹配實驗得到顏色匹配函數

  • 有負半軸是因為，並不能通過直接混合三原色以得到待測光，只能在待測光中加入三原色使得顏色匹配
    • 說明選擇的三原色所組成的空間並不能包含所有人類能感知到的顏色

\[C(C) \equiv R(R)+G(G)+B(B) \]

如果 C = 1，也就是滿足 \(C=\frac{R}{R+G+B}(R)+\frac{G}{R+G+B}(G)+\frac{B}{R+G+B}(B)(3)\)

SPD（Spectral Power Distribution）是指光源的光譜功率分佈。SPD 是一個曲線圖，顯示了特定光源產生的每個波長的光的功率（強度）

格拉斯曼定律告訴我們人類對色彩的感知（大約）是線性的

  • 對於已知 SPD 曲線 \(I(\lambda)\) 的光源，可以對顏色匹配函數求積分以得到它的三色刺激值
  • 給定兩個 SPD 曲線，如果算出來的三色刺激值是相同的，則感知到的顏色也是相同的

\[ \begin{aligned} R & =\int_0^{\infty} I(\lambda) \bar{r}(\lambda) d \lambda \\ G & =\int_0^{\infty} I(\lambda) \bar{g}(\lambda) d \lambda \\ B & =\int_0^{\infty} I(\lambda) \bar{b}(\lambda) d \lambda \end{aligned} \]

色度圖

我們稱 \(r=\frac{R}{R+G+B}(R)\)、\(g=\frac{G}{R+G+B}(R)\) 和 \(b=\frac{B}{R+G+B}(R)\) 為色度座標（chromaticity coordinates），我們只要知道任意兩個座標的值，就能算出第三個座標的值

連線各個波長的色度座標形成光譜軌跡，將光譜軌跡內的混合色繪製出來以得到色度圖

CIE XYZ

通過對 CIE RGB 做線性變換的到 CIE XYZ 色彩空間，定義了三個新的顏色匹配函數 \(\bar{x}(\lambda)\)、\(\bar{y}(\lambda)\)、\(\bar{z}(\lambda)\)

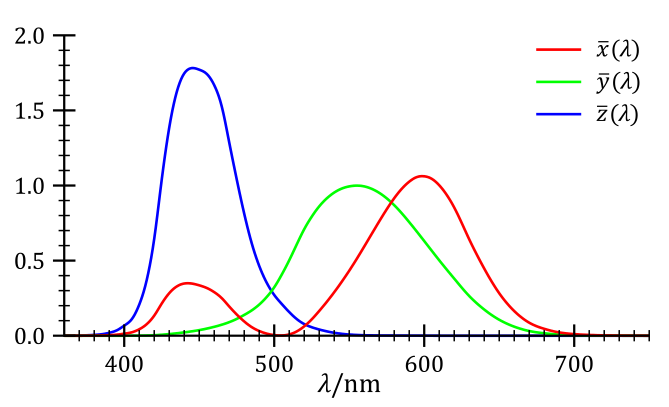
它有如下性質

  • 新的顏色匹配函數在所有地方都大於等於零
  • \(\bar{y}(\lambda)\) 等於光度函數（luminosity function），是表示亮度的分量

CIE XYZ 的色度圖（事實上，色度圖是三維曲線，我們看到的是它在 xy 平面上的投影）：

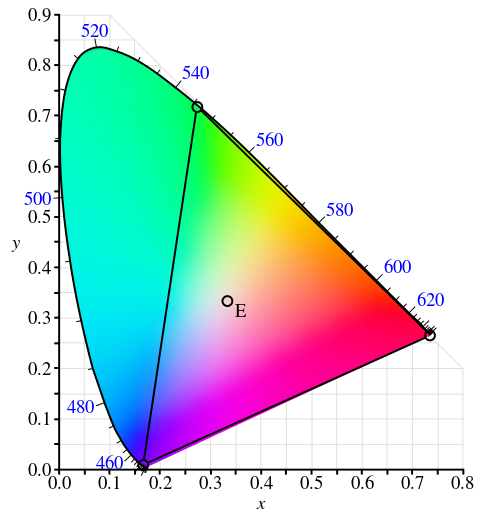
  • 色度圖中 E 點是白光，它被定義為 x=1/3，y=1/3，z=1/3
  • 沿著光譜軌跡能得到各種色調
  • 遠離 E 點顏色的飽和度變高

CIE LAB

CIE XYZ 並不是感知統一（perceptually uniform）的色彩空間，色度圖上任何兩種顏色之間的歐幾里德距離不能用作感知色差的統一度量，從 520nm 到 560nm 看起來都是綠色的，但從 460 納米到 500 納米，包含了更廣泛的顏色集

CIE LAB 是一種感知統一的色彩空間

  • L 分量基本符合人類對亮度的認知

YUV

常用於視訊編碼的色彩空間，基於人類對亮度更加敏感這個事實設計，Y 表示亮度，UV 表示色度，每個畫素都有一個 Y 取樣，但一組畫素會共用 U，V 取樣

YUV 並不是絕對色彩空間（absolute color space）

  • 絕對色彩空間是不依賴任何外部因素就可以準確表示顏色的色彩空間，比如 CIE LAB
  • YUV 只是對 RGB 資訊的編碼，具體的顏色取決於採用的 RGB 三原色

sRGB

儘管 CIE XYZ 是標準色彩空間（canonical color space），但影象和裝置並不會直接使用它，CIE XYZ 衍生出了許多其他色彩空間，比如 sRGB、NTSC 等

1996 年，微軟和 HP 定義了標準的 RGB 原語，且白點被定義為 D65 光源，這個色彩空間被稱為 standard RGB（sRGB）

  • 定義了白點意味著 sRGB 是假設了觀看條件的
  • sRGB 空間是 CIE XYZ 的子空間

從 XYZ 做線性變換可以得到線性 sRGB 空間

從線性 sRGB 空間到 sRGB 空間還需要做伽馬編碼

伽馬編碼

人眼對亮度的感知不是線性的，對較暗的光線更敏感，但對較強的光線不是那麼敏感，如果不對影象做伽馬編碼，就會為人類無法區分的高亮度分配太多的位元，而為人類敏感的低亮度分配太少的位元

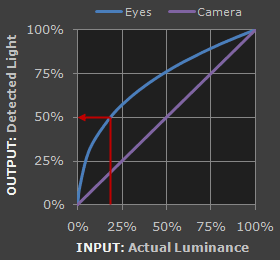
因此我們會對影象資訊做如下的非線性變換，稱為伽馬編碼

\[V_{out}=AV_{in}^{\frac{1}{\gamma}} \]

其中 \({\gamma}\) 是伽馬值，sRGB 的伽馬值約等於 2.2

伽馬編碼會用更大的區間來表示低亮度，用更小的區間表示高亮度

CRT 顯示器有一個電子特性是光強和電壓並不是線性的，而且表現出的關係也符合伽馬編碼，只不過 \({\gamma}\) 的值是負數，利用這個特性 sRGB 影象可以不做解碼直接在 CRT 顯示器上輸出

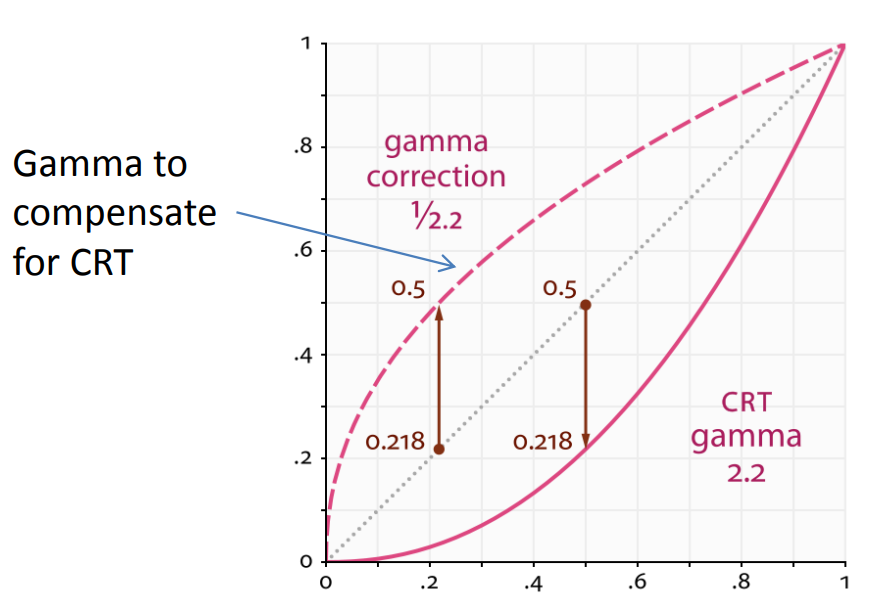
色感一致性

真實場景中，物體的 SPD 反映了物體的反射特性和場景光，我們的視覺系統會去適應場景光，比如同一個蘋果，在白天和傍晚的 SPD 是不同的，但我們看來卻都是紅色，這種現象叫色感一致性（color constancy）

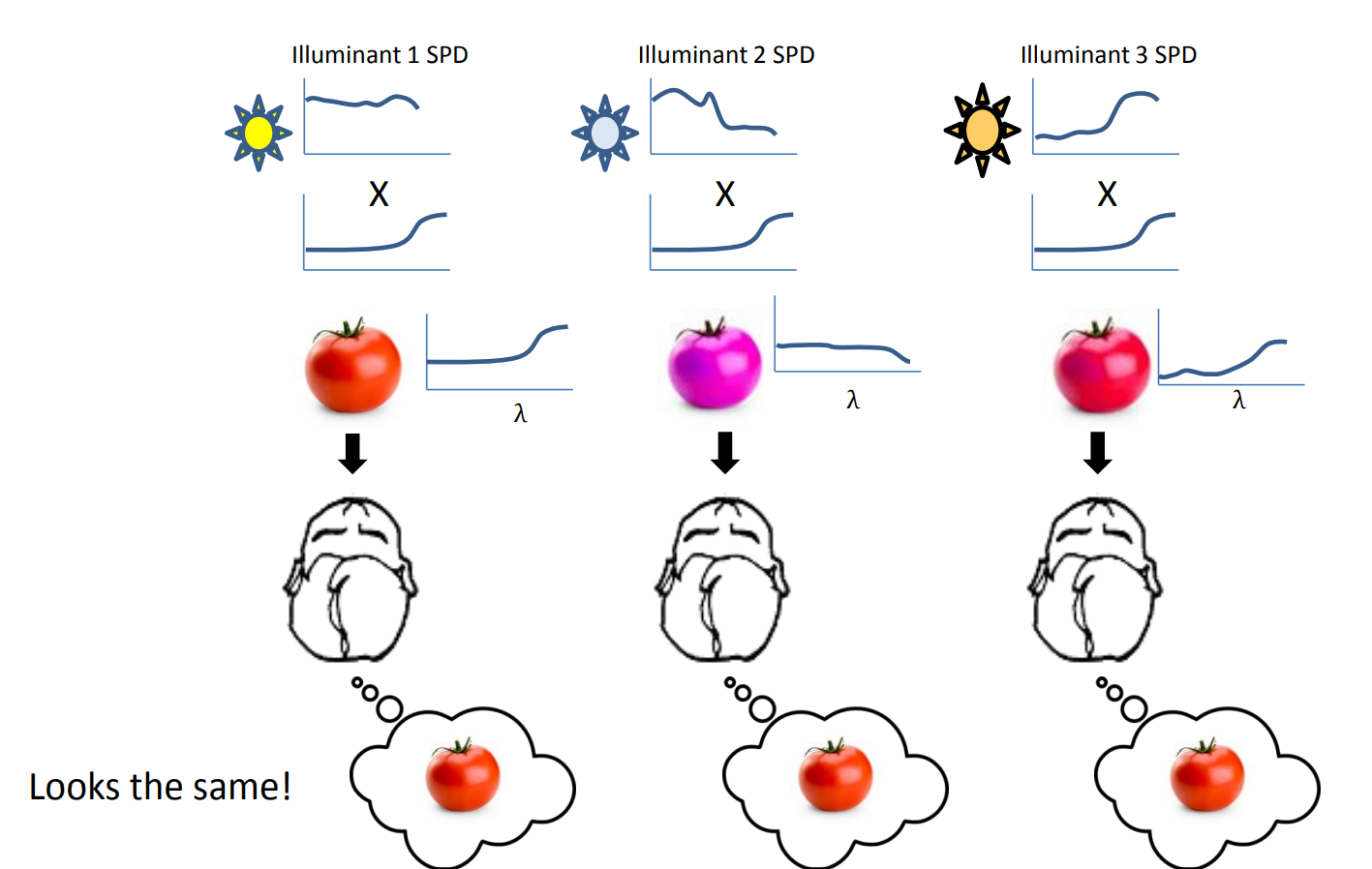
相機的感測器並沒有這種功能，因此影象處理階段需要做白平衡

  • 因為我們的眼睛沒法適應照片裡的光照，只能適應你觀看照片時的場景光

色溫

光源色溫的定義為與此光源發出相似的光的黑體輻射體所具有的開爾文溫度

  • 在熱力學中，黑體是一個理想化的物體，它能夠吸收外來的全部電磁輻射，並且不會有任何的反射與透射。隨著溫度上升，黑體所輻射出來的電磁波與光線則稱做黑體輻射
  • 在實際應用中，只有當光源發出的光和黑體輻射的光類似時，色溫才有定義。也就是，紅-橙-黃-白-淺藍這些顏色。當討論色溫時，討論例如綠色、紫色的色溫是沒有意義的

我們常常用光源的色溫來描述光源

下圖在 CIE xy 色度圖中標出了不同溫度下黑體光源的色度

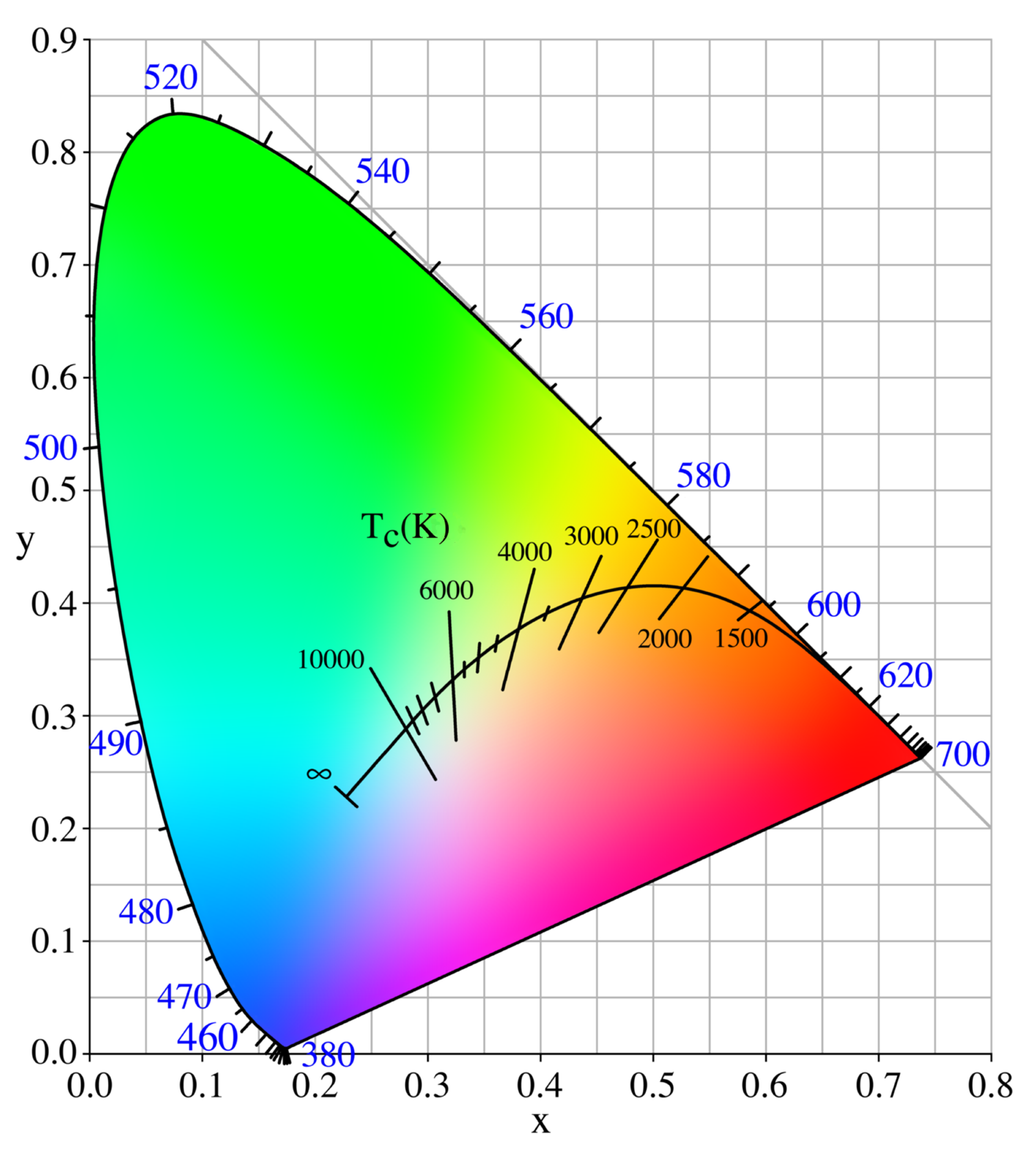
CIE 定義了一組標準光源，它們可以作為真實光源的參考

光源的 SPD 同樣可以轉換為三刺激值，並被正則化為色度座標，這個座標就白點

色彩適應（chromatic adaptation）的想法就是讓不同場景裡的白點看起來一樣

色彩適應

von Kries 模型

von Kries 模型是一種色彩適應方法

人類三種視錐細胞的反應記作 L、M、S，對於給定的刺激 \(i_r(\lambda)\)，我們可以這樣來計算它們

\[\begin{array}{rcl} L &=& k\int_{\lambda} \bar{l}(\lambda) i_r(\lambda) d\lambda \nonumber \\ M &=& k\int_{\lambda} \bar{m}(\lambda) i_r(\lambda) d\lambda \nonumber \\ S &=& k\int_{\lambda} \bar{s}(\lambda) i_r(\lambda) d\lambda \end{array} \]

其中，\(\bar{l}(\lambda)\)、\(\bar{m}(\lambda)\) 和 \(\bar{s}(\lambda)\) 是三種視錐細胞的光譜靈敏度函數（spectral sensitivity function）

\(i_r(\lambda)\) 來自於

\[i_r(\lambda) = i(\lambda) r(\lambda) \]

其中，\(i(\lambda)\) 表示光源，\(r(\lambda)\) 表示給定平面的光譜反射率（spectral reflectivity）

von Kries 模型用來預測觀測條件變化後，視錐細胞的反映，觀測條件的變化主要指光源的變化，假設 \(i(\lambda)\) 被另一個光源 \(i_a(\lambda)\) 替換掉，此時錐細胞的反應我們記作 \(L_a\)、\(M_a\) 和 \(S_a\)

\[\left [ \begin{array}{@{}l@{}} L_{a} \\ M_{a} \\ S_{a} \\ \end{array} \right ] = \left [ \begin{array}{@{}lll@{}} k_L & 0 & 0 \\ 0 & k_M & 0 \\ 0 & 0 & k_S \\ \end{array} \right ] \left [ \begin{array}{@{}l@{}} L \\ M \\ S \\ \end{array} \right ] \]

比例係數通常使用 \(k_L=L_{max}a/L_{max}\)、 \(k_M=M_{max}a/M_{max}\)、 \(k_S=S_{max}a/S_{max}\)，帶 max 下標的符號表示給定光源下 LMS 視錐細胞對白點刺激的最大反應

雖然 von Kries 模型是在 LMS 色彩空間中定義的，但可以做 3x3 的變換以放到 XYZ 色彩空間中使用

\[\left [ \begin{array}{@{}l@{}} L \\ M \\ S \\ \end{array} \right ] = \mathbf{M} \left [ \begin{array}{@{}l@{}} X \\ Y \\ Z \\ \end{array} \right ]. \]

參考材料