論文資訊

論文標題：Contrastive Adaptation Network for Unsupervised Domain Adaptation
論文作者：Guoliang Kang, Lu Jiang, Yi Yang, Alexander G Hauptmann
論文來源：CVPR 2019
論文地址：download 
論文程式碼：download

1 Preface

　　出發點： 

• • 無監督域自適應（UDA）對目標域資料進行預測，而標籤僅在源域中可用；
  • 以往的方法將忽略類資訊的域差異最小化，可能導致錯位和泛化效能差；

　　例子：

　　

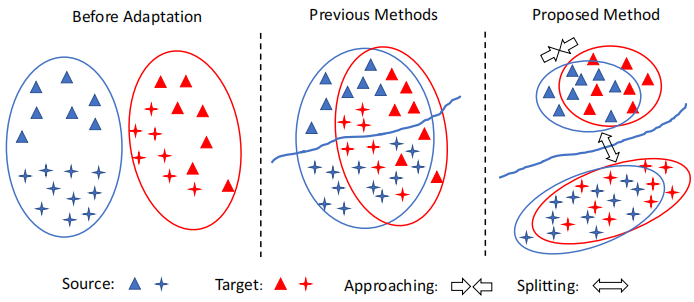
　　Left：在適應之前，源資料和目標資料之間存在域偏移；Middle：類不可知的自適應在域級將源資料和目標資料對齊，忽略了樣本的類標籤，因此可能導致次優解。因此，一個標籤的目標樣本可能與不同標籤的源樣本不一致；Right：我們的方法執行跨域的類感知對齊。為了避免錯位，只減少了類內域的差異。將類間域差異最大化，提高了模型的泛化能力。

　　Middle 中的先前方法存在的問題：First, samples of different classes may be aligned incorrectly, e.g. both MMD and JMMD can be minimized even when the target-domain samples are misaligned with the source-domain samples of a different class. Second, the learned decision boundary may generalize poorly for the target domain.

　　本文提出的 CAN 網路（Contrastive Adaptation Network）優化了一個顯式地對類內域差異和類間域差異建模的新度量，設計了一種交替更新 （alternating update）的訓練策略，可以端到端（end-to-end）的方式進行。

　　MMD 距離（Maximum mean discrepancy)，度量在再生希爾伯特空間中兩個分佈的距離，是一種核學習方法。 兩個隨機變數的距離為：

　　　　$\operatorname{MMD}[\mathcal{F}, p, q] := \underset{f \in \mathcal{F}}{\text{sup}} \left(\mathbf{E}_{p}[f(x)]-\mathbf{E}_{q}[f(y)]\right)$

　　　　$\operatorname{MMD}[\mathcal{F}, X, Y] :=\underset{f \in \mathcal{F}}{\text{sup}}\left(\frac{1}{m} \sum\limits _{i=1}^{m} f\left(x_{i}\right)-\frac{1}{n} \sum\limits_{i=1}^{n} f\left(y_{i}\right)\right)$

　　MMD距離的原始定義如上，$f$ 為屬於函數域  $\mathcal{F}$ 中的函數，直觀上理解就是兩個分佈經過一個定 義好的函數域 $\mathcal{F}$ 中的任意函數  $f$  對映後的期望之差的最大值（上界）。在實際應用中，對映後的期望，通過樣本均值來估計。一個直觀的理解就是如果兩個分佈一樣時，那麼只要取樣的樣本足夠多，那麼不論函數域怎麼定義，其 MMD 距離都是 $0$，因為不論通過什麼樣的函數對映後，兩個一樣的分佈對映後的分佈還是一樣的，那麼他們的期望之差都為 $0$ ，上界也就是 $0$。

4 Method

　　所提出的對比域差異（CDD）是基於條件資料分佈之間的差異。MMD 沒有對資料分佈的型別（例如邊際或條件）的任何限制，MMD 可以方便地測量 $P\left(\phi\left(\boldsymbol{X}^{s}\right) \mid Y^{s}\right)$ 和 $Q\left(\phi\left(\boldsymbol{X}^{t}\right) \mid Y^{t}\right)$ 之間的差異：

　　　　$\mathcal{D}_{\mathcal{H}}(P, Q) \triangleq   \sup _{f \sim \mathcal{H}}\left(\mathbb{E}_{\boldsymbol{X}^{s}}\left[f\left(\phi\left(\boldsymbol{X}^{s}\right) \mid Y^{s}\right)\right]-\mathbb{E}_{\boldsymbol{X}^{t}}\left[f\left(\phi\left(\boldsymbol{X}^{t}\right) \mid Y^{t}\right)\right]\right)_{\mathcal{H}}$

　　　　$\mu_{c c^{\prime}}\left(y, y^{\prime}\right)=\left\{\begin{array}{ll}1 & \text { if } y=c, y^{\prime}=c^{\prime} \\0 & \text { otherwise }\end{array}\right.$

　　其中，$c_1$ 和 $c_2$ 可以是不同的類，也可以是相同的類。

　　對於兩類 $c_1$ 和 $c_2$，$\mathcal{D}_{\mathcal{H}}(P, Q)$ 平方的核平均嵌入估計為：

　　　　$ \hat{\mathcal{D}}^{c_{1} c_{2}}\left(\hat{y}_{1}^{t}, \hat{y}_{2}^{t}, \cdots, \hat{y}_{n_{t}}^{t}, \phi\right)=e_{1}+e_{2}-2 e_{3}   \quad \quad\quad(3) $

　　Note：$\text{Eq.3}$ 定義了兩種類感知域差異，1：當 $c_{1}=c_{2}=c$ 時，它測量類內域差異；2：當 $c_{1} \neq c_{2}$ 時，它成為類間域差異。

　　CDD 完整計算如下：

　　其中，$\hat{y}_{1}^{t}, \hat{y}_{2}^{t}, \cdots, \hat{y}_{n_{t}}^{t}$ 簡寫為  $\hat{y}_{1: n_{t}}^{t}$。

　　此外，通過最小化交叉熵損失來訓練具有標籤的源資料網路：

　　　　$\ell^{c e}=-\frac{1}{n^{\prime}} \sum\limits _{i^{\prime}=1}^{n_{s}^{\prime}} \log P_{\theta}\left(y_{i^{\prime}}^{s} \mid \boldsymbol{x}_{i^{\prime}}^{s}\right)\quad \quad\quad(7) $

　　其中，$y^{s} \in\{0,1, \cdots, M-1\}$ 代表源域中的樣本 $\boldsymbol{x}^{s}$ 的標籤，$P_{\theta}(y \mid \boldsymbol{x})$ 表示給定輸入 $\boldsymbol{x}$，用 $\theta$ 引數化的標籤 $y$ 的預測概率。

　　因此，總體目標可以表述為：

　　　　$\underset{\theta}{\text{min}}\quad   \ell=\ell^{c e}+\beta \hat{\mathcal{D}}_{\mathcal{L}}^{c d d}\quad \quad\quad(8) $

　　請注意，我們對標記的源資料進行獨立取樣，以最小化交叉熵損失 $\ell^{c e}$，並估計 $\operatorname{CDD} \hat{\mathcal{D}}_{\mathcal{L}}^{c d d}$。通過這種方式，我們能夠設計更有效的取樣策略，以促進 CDD 的小批次隨機優化，同時不干擾標記源資料的交叉熵損失的傳統優化。

4.4 Optimizing CAN

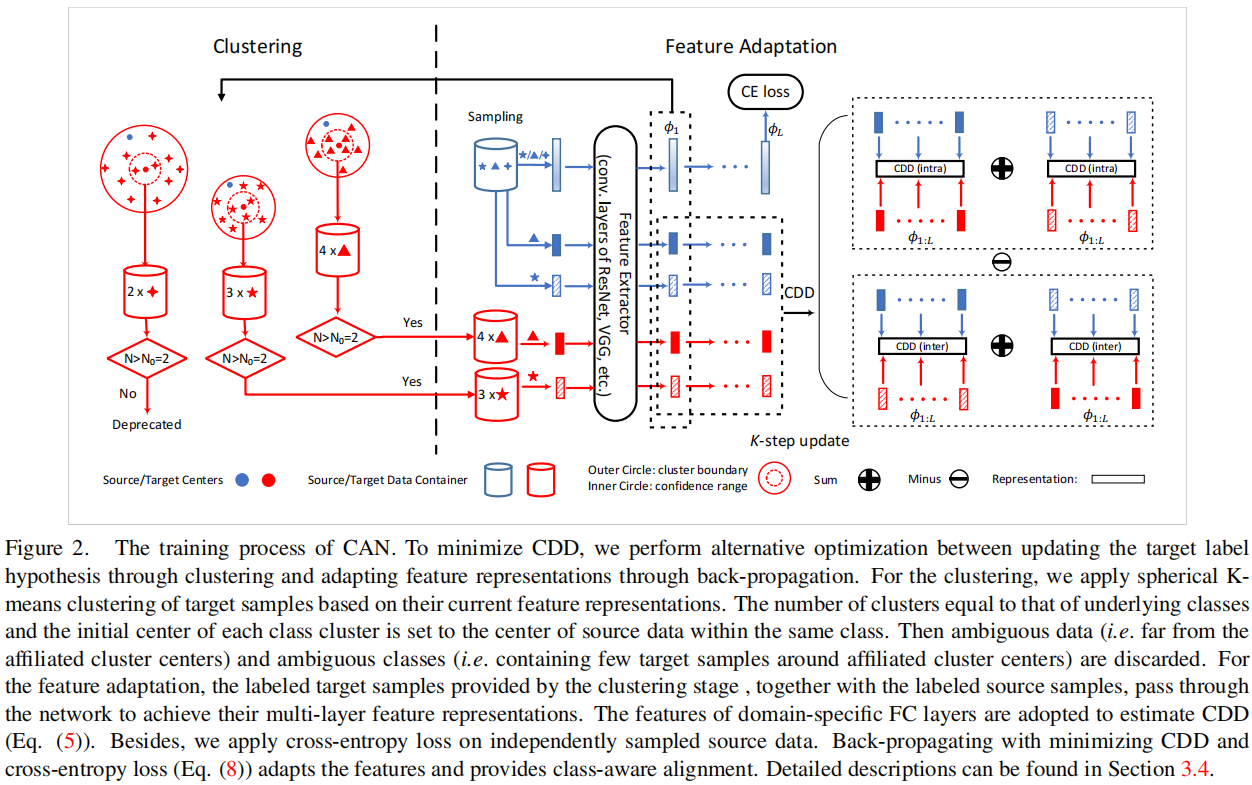
　　CAN 的框架如 Figure2 所示。在本節中，我們主要集中討論如何儘量減少 CAN 中的 CDD 損失。

　　

4.4.1 Alternative optimization (AO)

　　如 $\text{Eq.5}$ 中所示，我們需要共同優化目標標籤假設 $\hat{y}_{1: n_{t}}^{t}$ 和特徵表示 $\phi_{1: L}$，本文采用了交替優化來執行這種優化。

　　假設有 $M$ 類，所以可以設定 $\mathrm{K}=\mathrm{M}$ 。

　　步驟：

　　1）使用源域的資料的表徵計算每個類別的樣本編碼中心： $\mathrm{O}^{\mathrm{s}, \mathrm{c}}$  ，其中 $\mathrm{c}$ 是某個特定的類別，我們用這些源域中心初始化目標域的聚類的中心 $\mathrm{O}^{\mathrm{t}, \mathrm{c}}$ ，其中：

　　　　$\mathrm{O}^{\mathrm{sc}}=\sum_{i=1}^{\mathrm{n}_{\mathrm{s}}} 1_{y_{i}^{\mathrm{s}}=\mathrm{c}} \frac{\phi_{1}\left(\mathrm{x}_{\mathrm{i}}^{\mathrm{s}}\right)}{\left.\| \mathrm{x}_{\mathrm{i}}\right) \|}$$

　　　　$1_{y_{\mathrm{i}}^{\mathrm{s}}=\mathrm{c}}=\left\{\begin{array}{ll}1 & \text { if } \mathrm{y}_{\mathrm{i}}^{\mathrm{s}}=\mathrm{c} ; \\0 & \text { otherwise. }\end{array}, \mathrm{c}=\{0,1, \ldots, \mathrm{M}-1\}\right.$

　　2）計算樣本與中心之間的距離，我們使用餘弦距離，即：$\operatorname{dist}(\mathrm{a}, \mathrm{b})=\frac{1}{2}\left(1-\frac{\mathrm{a} \cdot \mathrm{b}}{\|\mathrm{a}\|\|\mathrm{b}\|}\right) $

　　3）聚類的過程是迭代的：

　　　　(1) 對每個目標域的樣本找到所對應的聚類中心: $\hat{y}_{\mathrm{i}}^{\mathrm{t}}=\underset{c}{\arg \min \operatorname{dist}}\left(\phi\left(\mathrm{x}_{\mathrm{i}}^{\mathrm{t}}\right), \mathrm{O}^{\mathrm{tc}}\right) $;

　　　　(2) 更新聚類中心: $\mathrm{O}^{\mathrm{tc}} \leftarrow \sum_{\mathrm{i}=1}^{\mathrm{N}_{\mathrm{t}}} 1_{\hat{y}_{\mathrm{i}}^{\mathrm{t}}=\mathrm{c}}\frac{\phi_{1}\left(\mathrm{x}_{\mathrm{t}}^{\mathrm{t}}\right)}{\left\|\phi_{1}\left(\mathrm{x}_{\mathrm{i}}\right)\right\|}$

　　迭代直到收斂或者抵達最大聚類步數停止；
　　4）聚類結束後，每個目標域的樣本 $\mathrm{x}_{\mathrm{i}}^{\mathrm{t}}$ 被賦予一個標籤 $ \hat{y}_{\mathrm{i}}^{\mathrm{t}}$；
　　5）此外，設定一個閾值 $\mathrm{D}_{0} \in[0,1]$  ，將屬於某個簇但是距離仍然超過給定閾值的資料樣本刪除，不參與本次計算 CDD，僅保留距離小於 $\mathrm{D}_{0}$ 的樣本：

　　　　$\hat{\mathcal{T}}=\left(\mathrm{x}^{\mathrm{t}}, \hat{\mathrm{y}}^{\mathrm{t}}\right) \mid \operatorname{dist}\left(\phi_{1}\left(\mathrm{x}^{\mathrm{t}}\right), \mathrm{O}^{\mathrm{t}, \hat{\mathrm{y}}^{\mathrm{t}}}\right)<\mathrm{D}_{0}, \mathrm{x}^{\mathrm{t}} \in \mathcal{T}$

　　6）此外，為了提供更準確的樣本分佈的統計資料，假設每個類別挑選出來的集合 $ \hat{\mathcal{T}}$ 的大小至少包含某個數量 $N_{0}$ 的樣本，不然這個類別本次也不參與計算 CDD，即最後參與計算的類別集為: 

　　　　$\mathcal{C}_{T_{e}}=\left\{c \mid \sum_{i}^{|\mathcal{T}|} \mathbf{1}_{\hat{y}_{i}^{t}=c}>N_{0}, c \in \{0,1, \cdots, M-1\} \right \}  $

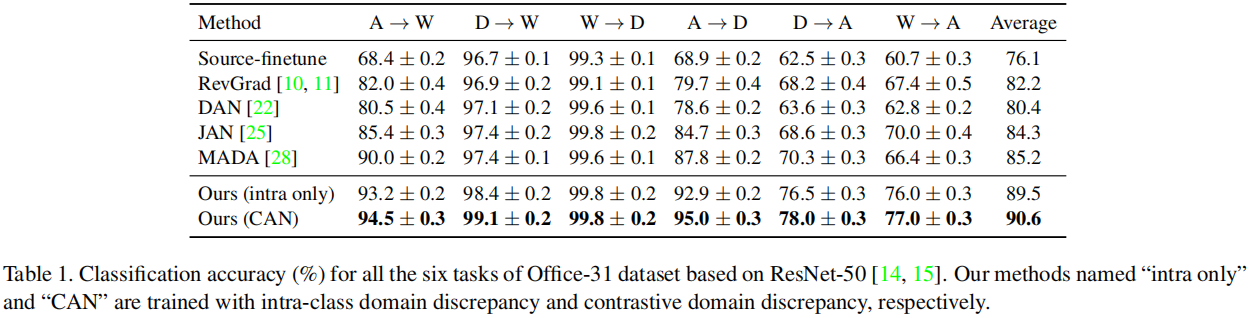
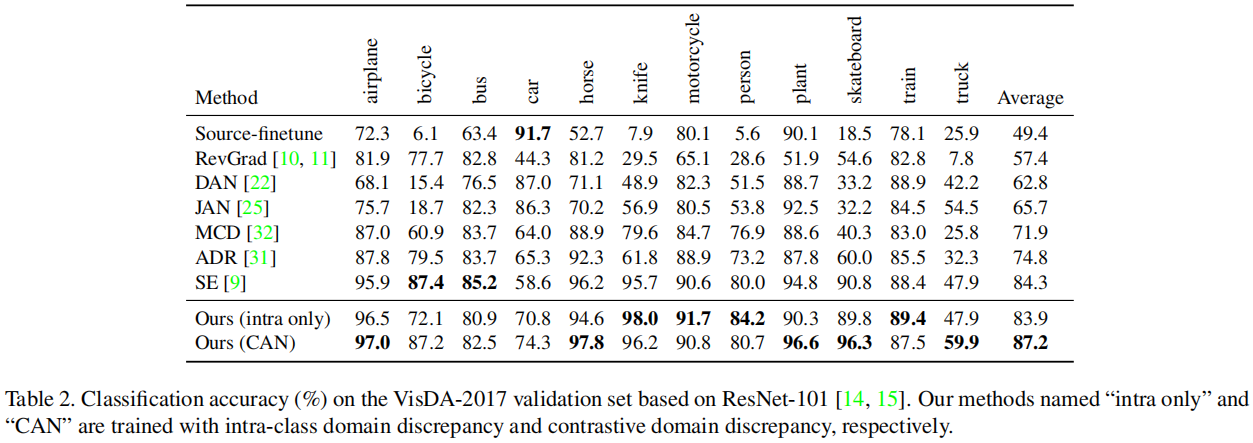
5 Experiment