貪婪演演算法Dijkstra

Dijkstra

最短路徑問題 : 給定一個帶權有向圖 G = (V, E, W)，同時給定一個源點 u (u ∈ V)，我們要找出從源點 u 出發到其它各點的最短路徑距離，並得出這些最短路徑的具體路徑有哪些邊構成。

其實我們要求的就是從 源點 u 出發到 其它各點 str的最短路徑所組成的路線網路，也就是一個 最短路徑樹。

最短路徑問題 : 給定一個帶權有向圖 G = (V, E, W)，同時給定一個源點 u (u ∈ V)，我們要找出從源點 u 出發到其它各點的最短路徑距離，並得出這些最短路徑的具體路徑有哪些邊構成。

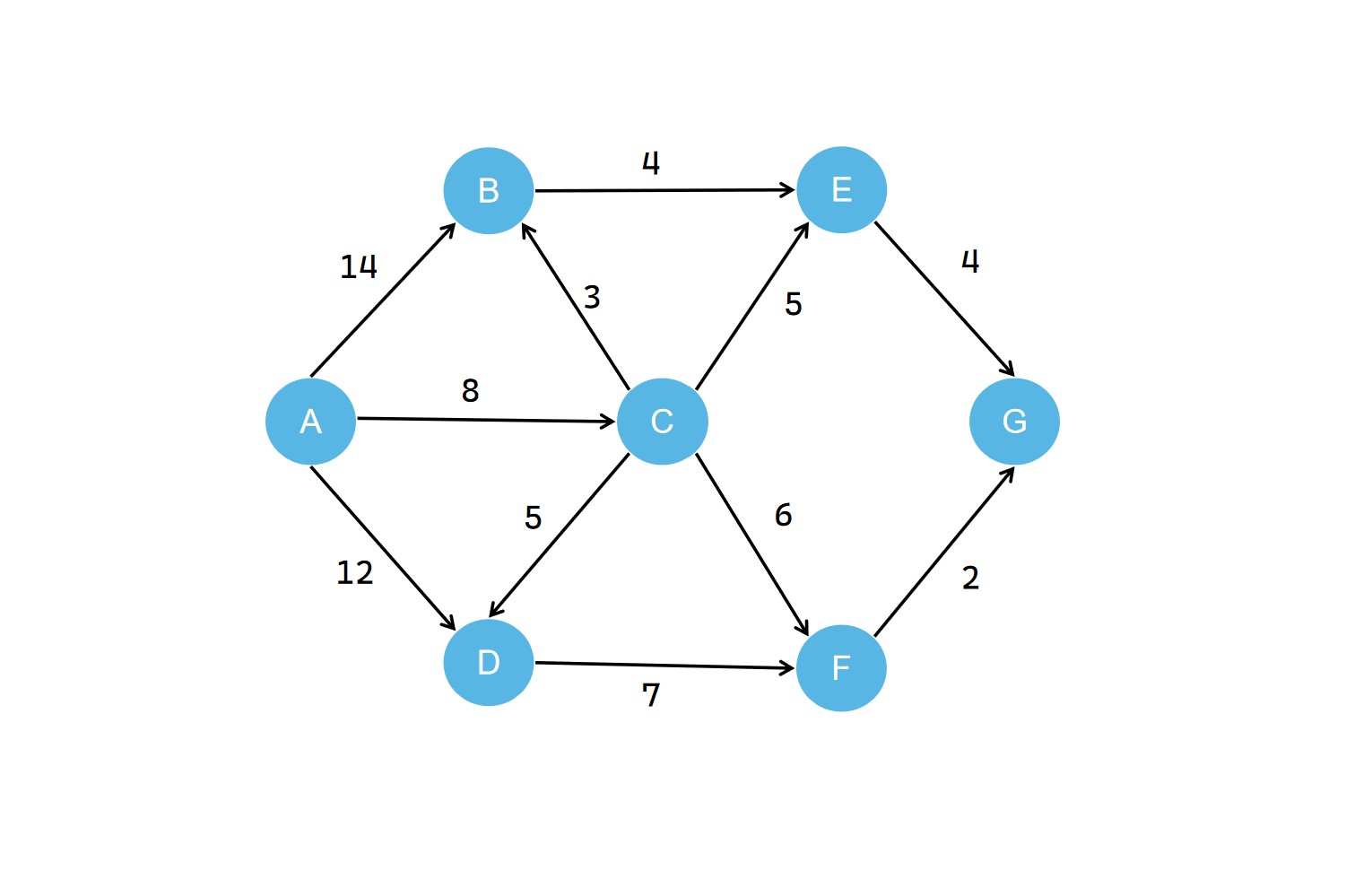
我們以下面這個帶權有向圖為範例

我們若以 A 為源點，得到如下的最短路徑

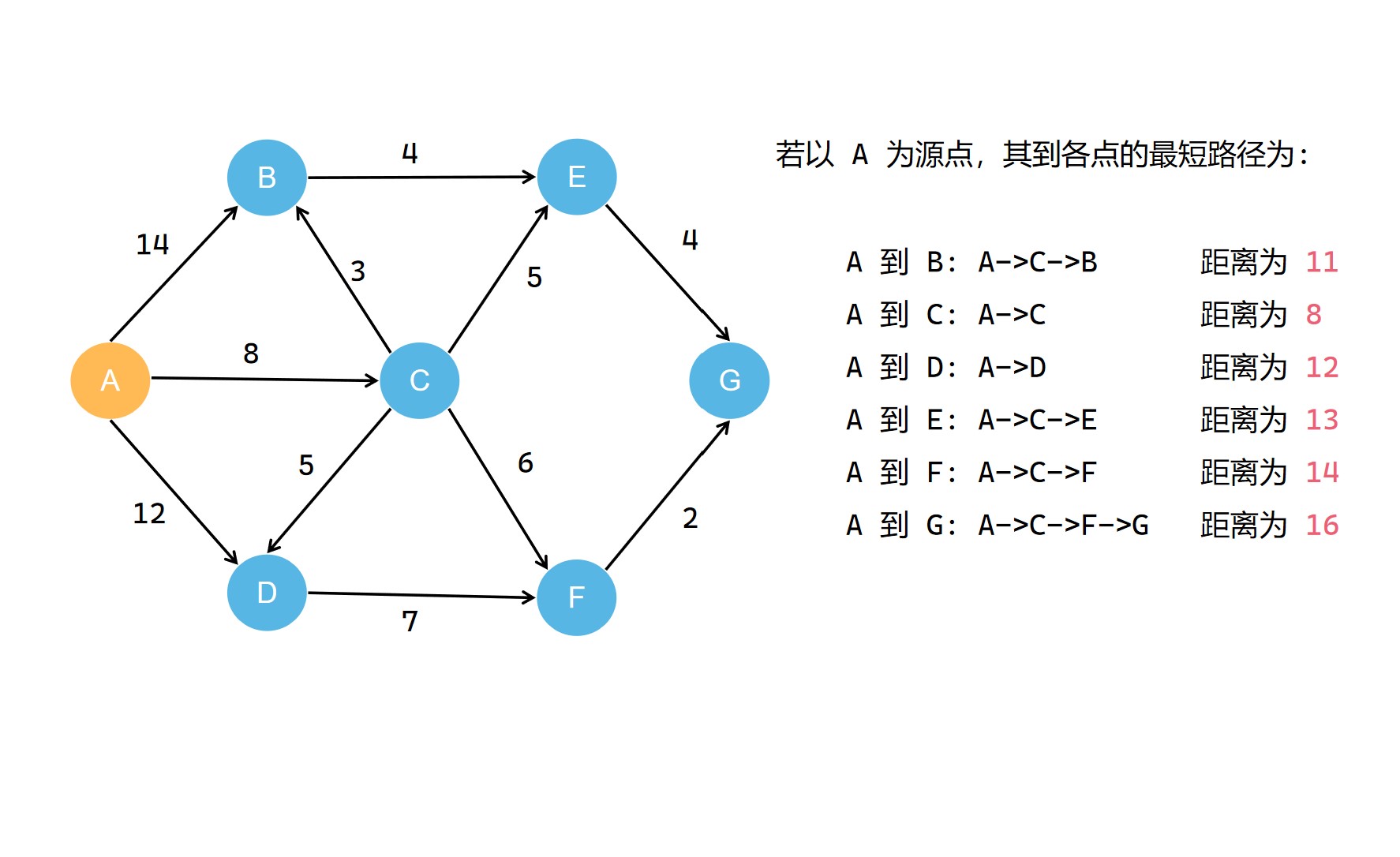
我們可以把源點到各點最短路徑用綠色標記一下

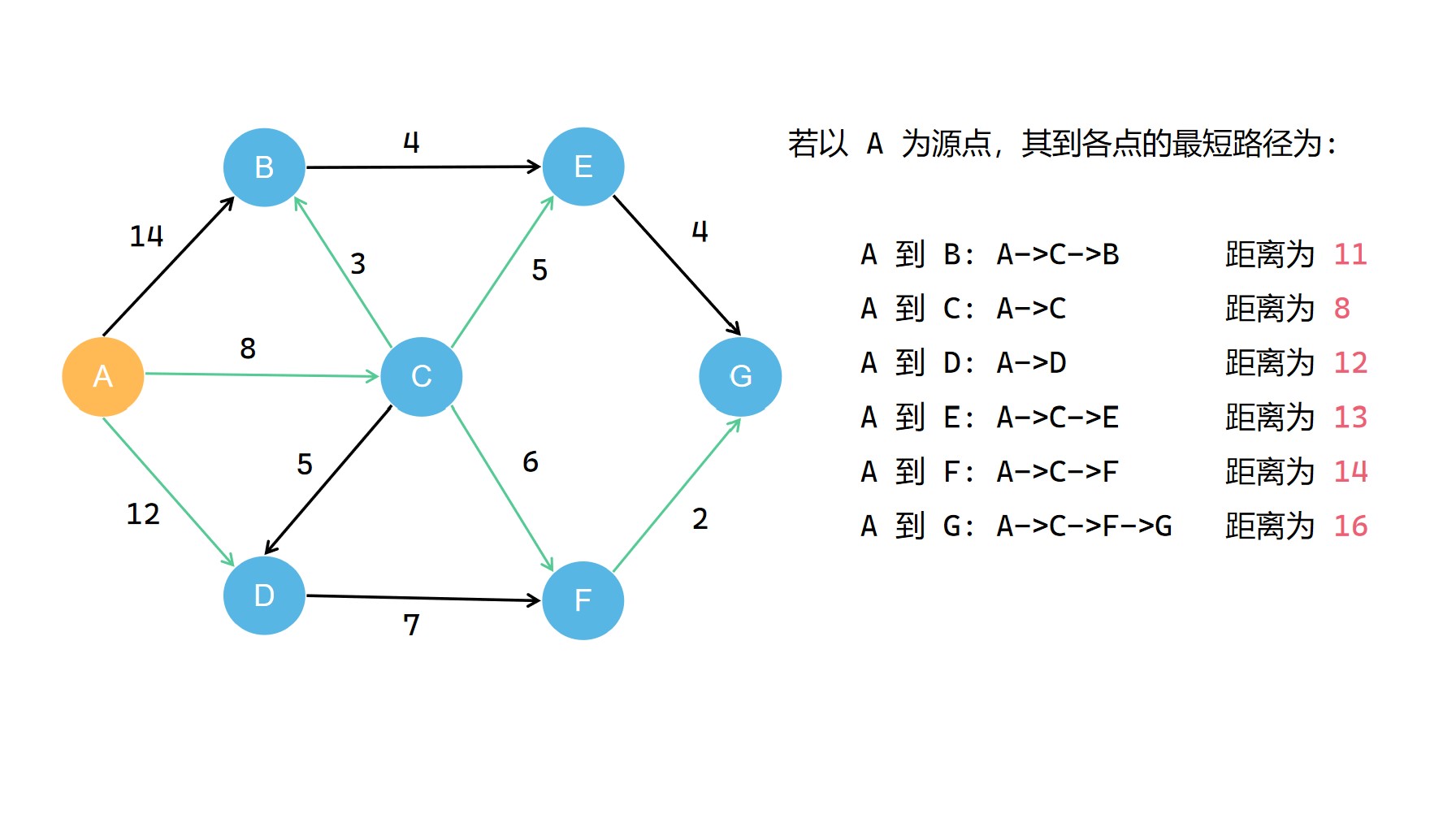
我們可以看出所有的最短路徑構成了一個最短路徑樹

我們要求的從 源點 到 其它各點 的最短路徑所組成的路線網路，就是這個最短路徑樹。

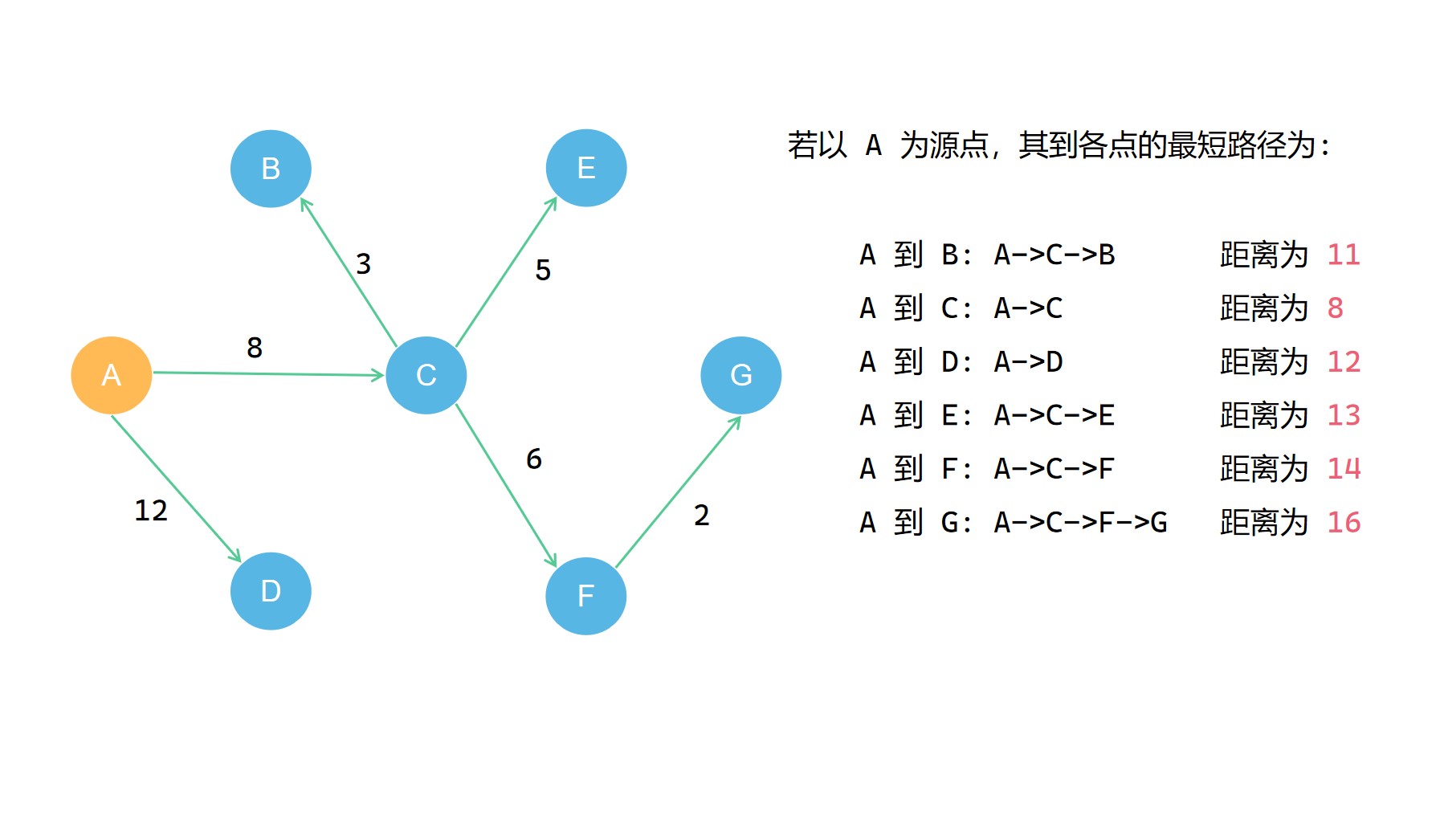
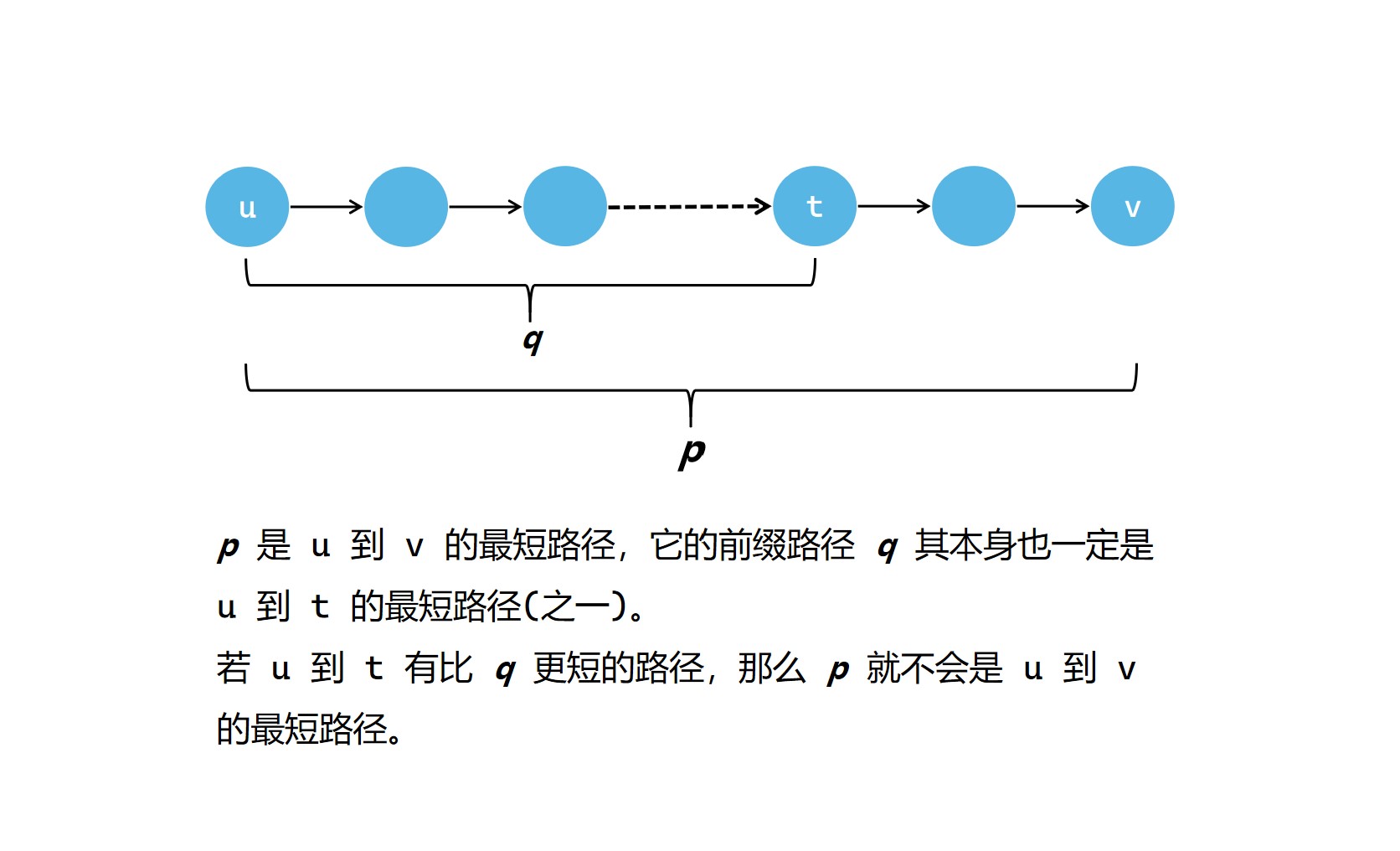
在上面的圖中，我們不難發現，當我們確定了源點 u 到某個其它的點 v 的最短路徑時，在這個最短路徑的具體路線中，若有一箇中轉點 t，那麼在這個最短路徑中從源點 u 到 t 的路徑也一定是 u 到 t 的最短路徑(之一)。也就是說，假設源點 u 到 v 的最短路徑為 p，那麼p任意的字首路徑 q 一定是最優的(最短路徑之一)。如果 q 不是最優的，那麼就會存在另一個更短的路徑比 p 更短。

這個性質還是很重要的，是解決單源最短路徑問題的核心

我們畫個圖來理解一下

歧義性

在上面的闡述中也稍微提到一點，就是最短路徑其實不一定是唯一的，有可能存在兩個路徑，它們的路徑距離一樣且都是最短的，那麼此時我們二選其一就可以啦。還有一個問題就是，我們的邊權都應當是正數，如果邊權存在非正數，那麼我們是無法定義這個圖中的最短路徑的(距離確實不能是非正數呀，除了自己到自己