點陣圖

概念

點陣圖： 所謂點陣圖，就是用每一位來存放某種狀態，適用於海量資料，資料無重複的場景。通常是用來判斷某個資料存不存在的。

適用場景： 如果我們需要對大量的資料進行處理，判斷該資料在不在，比如40億個整形資料，如果我們用unordered_set來存放這些資料，大約需要佔用16G的記憶體，顯然這是不妥的，如果我們選擇用一個資料結構，該資料結構可以存放40億個資料在不在的狀態，也就是開42億個位元位大小的空間（整形資料總共是約42億個），約500M，這樣就可以將資料存下去了。
如下圖： （其中1代表在，0代表不在，所以1，2，5，7這幾個元素是在的）

原理

補充知識

什麼是高地址、低地址？

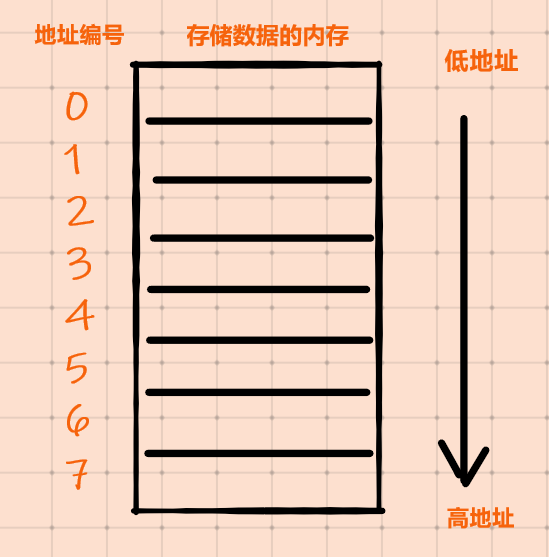
什麼是資料的低位、高位？

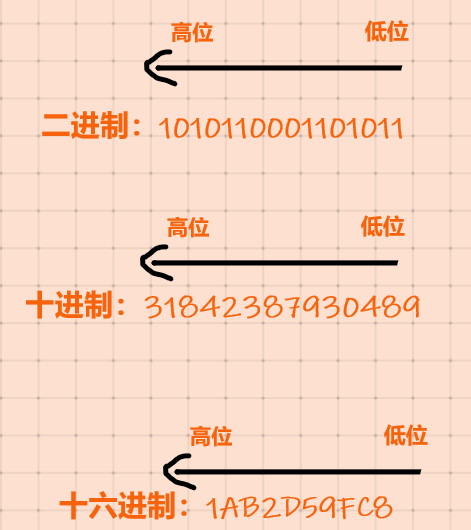
小端模式

資料的低位放在低地址空間，資料的高位放在高地址空間

範例講解

例子1：存放二進位制數：1011-0100-1111-0110-1000-1100-0001-0101

注意注意：我們在存放的時候是以一個儲存單元為單位來存放，儲存單元內部不需要再轉變順序啦！

就例如下面的低位0001-0101存放在0號地址，我們不需要把它變成1010-1000，不需要！！不需要！！

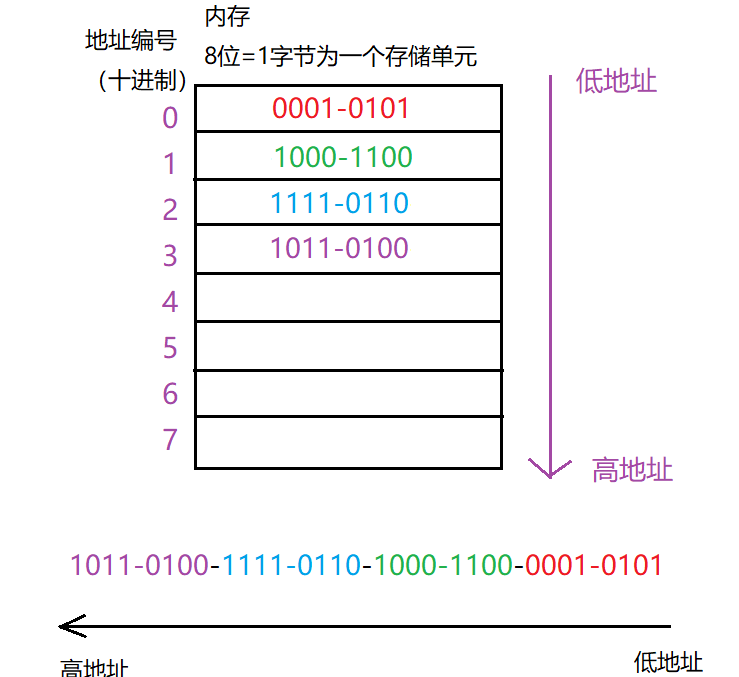
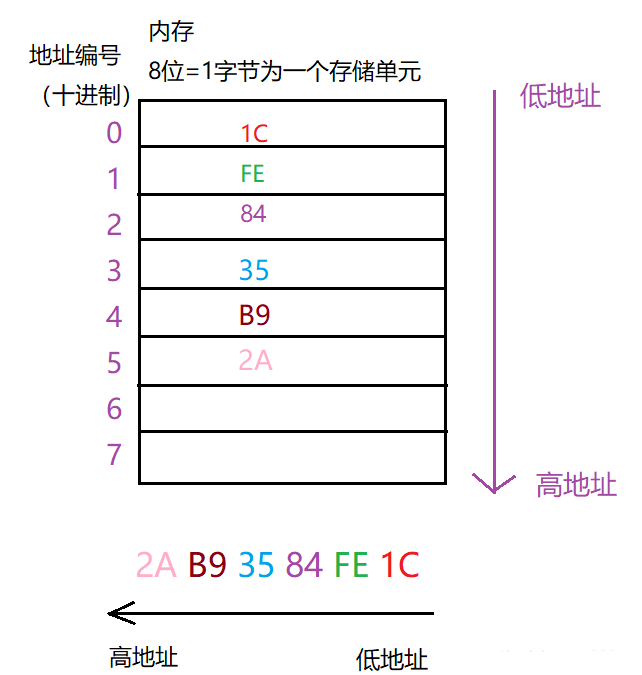
讀取資料：注意一定一定是從低地址讀起！！！我們知道這是小端儲存，所以在讀出來的時候會從低位開始放！！！

例子2：存放十六進位制數：2AB93584FE1C

十六進位制數每一位轉化為二進位制就是4位元：2對應0010，A對應1010，以此類推。所以在存放的時候兩個十六進位制位就佔用一個儲存單元

大端模式

資料的高位放在低地址空間，資料的低位放在高地址空間

範例演示：

例子1：存放二進位制數：1011-0100-1111-0110-1000-1100-0001-0101

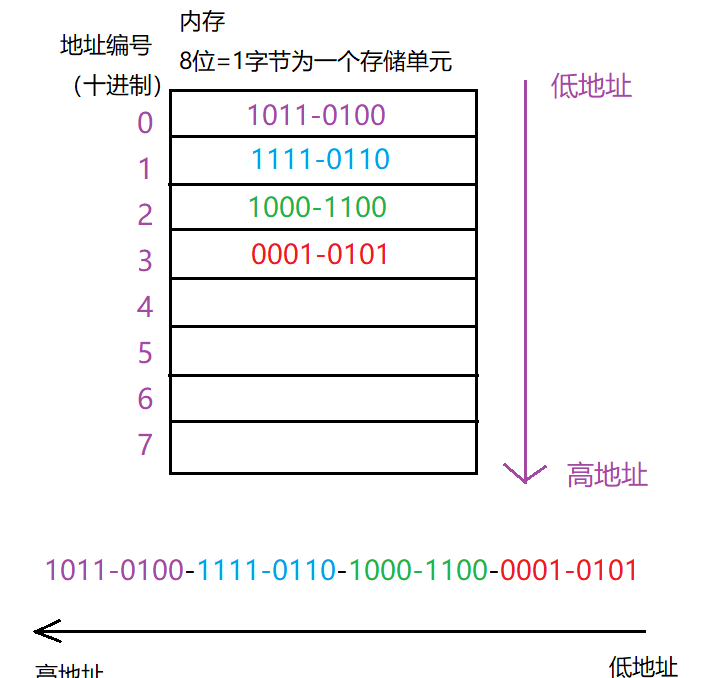
讀取資料：注意仍然是從低地址開始讀，我們知道這是大端模式，當我們從0號地址讀到1011-0100時，我們知道它是高位，所以放到高位的位置上去

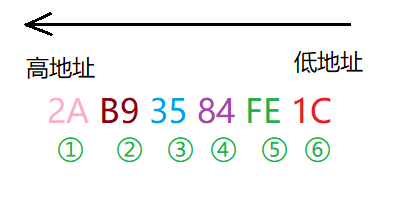
例子2：存放十六進位制數：2AB93584FE1C

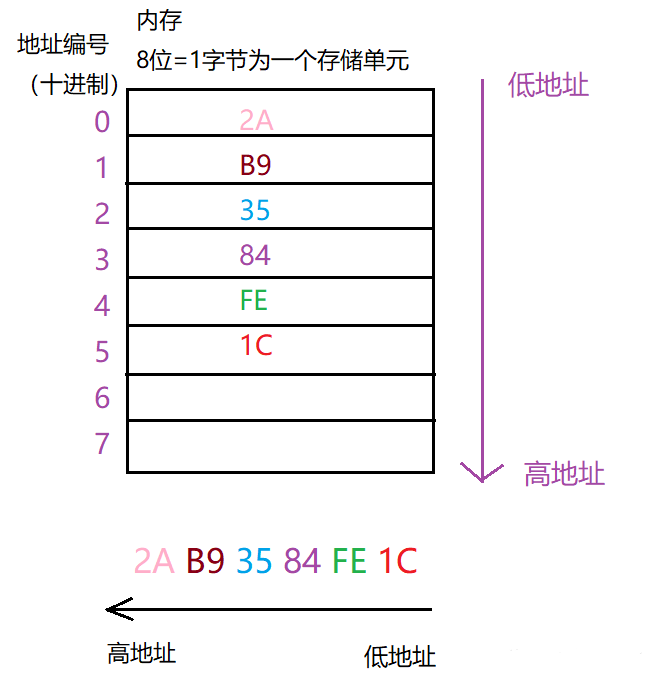
讀取資料：注意從低地址開始讀取，讀到的從高地址開始放！！！

點陣圖原理

點陣圖中的每個資料單元都是一個bit位，這樣子平時我們都要話32位元4位元組來儲存資料，而現在我們只需要花1個位元組就能」儲存資料」，在空間上減少了約32倍的容量。例如40G的資料我們只要花1.3G來儲存。但是我們平時操作的資料型別最小就是一個位元組，我們不能直接對位進行操作，所以我們可以藉助位運算來對資料進行操作。下面我們來看看資料在點陣圖中是如何儲存的
我們這裡給出一個陣列
int arr[] = {1,2,4,5,7,10,11,14,16,17,21,23,24,28,29,31}；則我們只需要花1個位元組來存這些資料

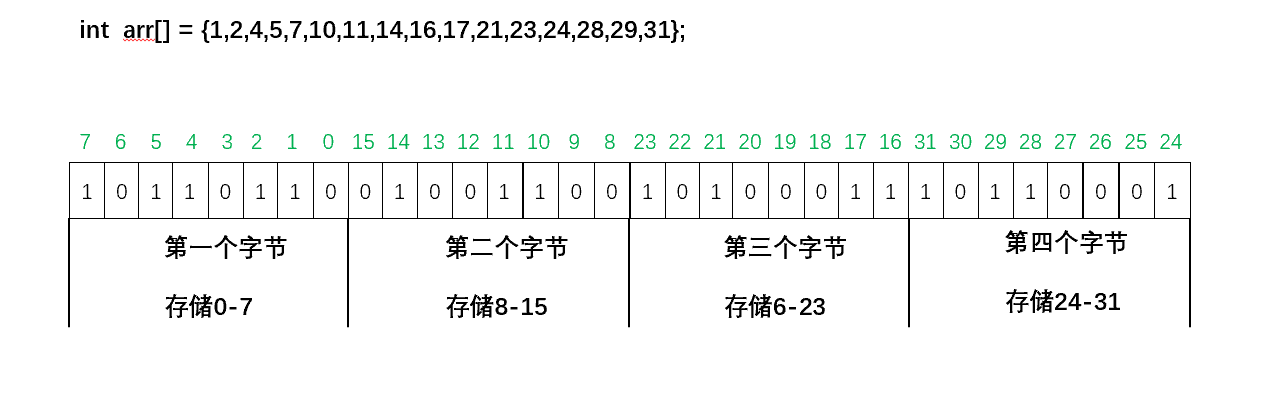
解釋：我們目前很多的機器都是小端儲存，也就是低地址存低位，一個整形資料中，第一個位元組用來儲存0-7的數位，第二個位元組用來儲存8-15的數位，第三個位元組用來儲存16-23的數位，第四個位元組用來儲存24-31的數位。我們來看看數位10是如何儲存的。先通過模上32，取餘還是10，然後再將4位元組中第10個位元位置為1，則表示該數位出現過。由於我們的機器是小端儲存，所以我們的每個位元位都是要從右邊開始計算的

所以說我們只需要將對應的位元位置為1即可。但是如果我們要儲存的資料很大呢？其實也很簡單，我們可以定義一個陣列，當做一個點陣圖，如果該數位在0-31之間，我們就儲存在0號下標的元素中進行操作，如果在32-63之間，則就在1號下標之間進行操作。計算下標我們可以通過模32來獲得下標

實現

整體框架

在實現點陣圖中，我們的成員變數只需要一個陣列就可以實現。而這個陣列有多我們要開多大呢？陣列多開一個整形空間，就能多存32個數位，所以我們可以讓使用者提供一個準確的數，這個數是一個資料量，也是數的最大範圍。我們可以通過該數模上32，就可以獲得該陣列的大小，但是0~31模上32為0，我們開0個空間那顯然不合適，所以我們要開bitCount/32 + 1個空間大小的陣列

class bitset
{
public:
	bitset(size_t bitCount)
		:bitCount(bitCount)
	{
		//resize會將vector中的元素初始化為0
		_bitset.resize(bitCount / 32 + 1);
	}
private:
	vector<int> _bitset;
	int bitCount;// 開num位元位的空間
};	

把某位置為1

分為三步：

1. 計算出x對應的陣列下標： 先確定這個數應該處在第幾個陣列中，也就是index=x/32
2. 計算處x在對應陣列中的位元位的位置： 通過把x對32取模，得到x在第index個整形的第pos個位置
3. 將計算出來的位元位置為1：操作位，我們可以通過位運算來操作，可以先將1左移pos位後再和整數進行或運算

舉例：假設pos=5，資料為10010011

1. 將1進行左移5位==>100000
2. 將資料和第一步計算出來的結果進行或運算----->10010011 | 100000 =10110011，此時我們就將指定位置置位1了

程式碼實現：

// 每個位元組用0和1記錄某個數位存在狀態
	// 把x所在的資料在點陣圖的那一位變成1
	void set(int x)
	{
		if (x > bitCount) return;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是第index個整數的第pos個位

		_bitset[index] |= (1 << pos);
	}

把某位置為0

分為兩步：

1. 找到那一位：和上面的方法一樣
2. 把這位設定為0：通過先將1進行左移pos位，然後取反，將結果再和原來資料進行與運算

舉例：假設pos=5，資料為10110011

1. 將1進行左移5位後並取反011111
2. 將第一步計算出來的結果和資料進行與運算----->10110011 & 011111 = 10010011，刪除成功

程式碼實現：

// 把x所在的資料在點陣圖的那一位變成0
	void reset(int x)
	{
		if (x > bitCount) return;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是滴index個整數的第pos個位
		_bitset[index] &= ~(1 << pos);
	}

判斷某位是否為1

分為兩步：

1. 找到那一位： 和上面的方法一樣
2. 把這位設定為0：將陣列下標為index的整數向右移pos位，然後再和1進行與運算，如果為1則表示存在，否則不存在

舉例：pos=5，資料為10110011

1. 將資料進行右移5位00000101
2. 將第一步計算出來的結果和1進行與運算----->00000101 & 1 = 1，此時表示該數位存在，返回true

// 判斷x是否存在
	bool test(int x)
	{
		if (x > bitCount) return false;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是滴index個整數的第pos個位

		return _bitset[index] & (1 << pos);
	}

完整程式碼以及測試

#define _CRT_SECURE_NO_WARNINGS
#include<iostream> //引入標頭檔案
#include<vector>
#include <string>
#include <new>
#include<algorithm> 
using namespace std; //標準名稱空間
class bitset
{
public:
	bitset(size_t bitCount)
		:bitCount(bitCount)
	{
		//resize會將vector中的元素初始化為0
		_bitset.resize(bitCount / 32 + 1);
	}
	// 每個位元組用0和1記錄某個數位存在狀態
	// 把x所在的資料在點陣圖的那一位變成1
	void set(int x)
	{
		if (x > bitCount) return;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是第index個整數的第pos個位

		_bitset[index] |= (1 << pos);
	}
	// 把x所在的資料在點陣圖的那一位變成0
	void reset(int x)
	{
		if (x > bitCount) return;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是滴index個整數的第pos個位
		_bitset[index] &= ~(1 << pos);
	}
	// 判斷x是否存在
	bool test(int x)
	{
		if (x > bitCount) return false;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是滴index個整數的第pos個位

		return _bitset[index] & (1 << pos);
	}

private:
	vector<int> _bitset;
	int bitCount;// 開num位元位的空間
};
void TesstBitset1()
{
	bitset bs(100);

	bs.set(99);
	bs.set(0);
	bs.set(98);
	bs.set(55);
	bs.set(75);
	bs.set(35);

	;
	bs.reset(99);
	bs.reset(87);

	for (size_t i = 0; i <= 100; ++i)
	{
		cout << i << ":" << bs.test(i) << " ";
		if (i != 0 && i % 10 == 0)
			cout << endl;
	}
}

int main() {
	TesstBitset1();
	system("pause");
	return EXIT_SUCCESS;
}

執行結果如下：

點陣圖的應用

有以下幾個：

1. 快速查詢某個資料是否在一個集合中
2. 排序+去重
3. 作業系統中磁碟的標記等

缺點： 只能處理整形資料

布隆過濾器

引入

我們在使用新聞使用者端看新聞時，它會給我們不停地推薦新的內容，它每次推薦時要去重，去掉那些已經看過的內容。問題來了，新聞使用者端推薦系統如何實現推播去重的？ 用伺服器記錄了使用者看過的所有歷史記錄，當推薦系統推薦新聞時會從每個使用者的歷史記錄裡進行篩選，過濾掉那些已經存在的記錄。

如何快速查詢？

1. 雜湊表： 用雜湊表儲存使用者的歷史記錄。缺點： 空間消耗比較大
2. 點陣圖： 用點陣圖儲存使用者的歷史記錄。 缺點： 點陣圖一般只能處理整形，如果內容編號是字串，就無法處理了。但我們可以使用一些雜湊演演算法把字串型別轉換成整型，比如BKDR雜湊演演算法，但是這裡還存在一個問題。字串的組合方式太多了，一個字元的取值有256種，一個數位只有10種，所以不可避免會出現雜湊衝突
3. 布隆過濾器： 將雜湊表和點陣圖結合使用。

概念

布隆過濾器是由布隆（Burton Howard Bloom）在1970年提出的一種緊湊的、比較巧妙的概率型資料結構，特點是高效地插入和查詢

布隆過濾器其實就是點陣圖的一個變形和延申，雖然無法避免雜湊衝突，但我們可以想辦法降低誤判的概率；當一個資料對映到點陣圖中時，布隆過濾器會用多個雜湊函數對映到多個位元位，當判斷一個資料是否在點陣圖當中時，需要分別根據這些雜湊函數計算出對應的位元位，位元位設定了代表著當前狀態的預設值，設定為 1 則判定為該資料存在，這一點很類似於我們定義紅黑數的節點顏色。

布隆過濾器使用多個雜湊函數進行對映，目的就在於降低雜湊衝突的概率，一個雜湊函數產生衝突的概率可能比較大，但多個雜湊函數同時產生衝突的概率可就沒那麼大了！
舉個例子：針對值 「source」 和三個不同的雜湊函數分別生成了雜湊值 2、4、7

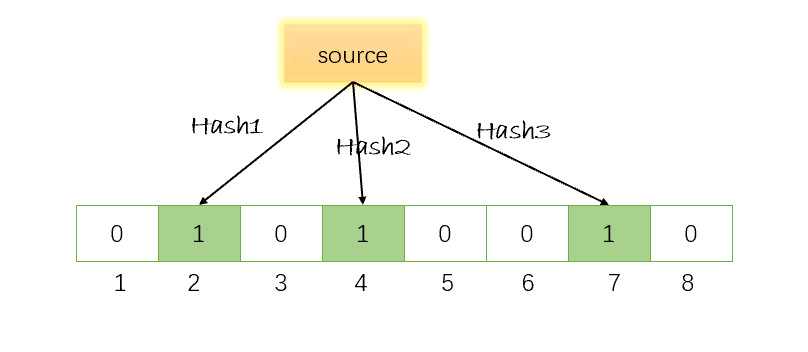
現在，如果我們要查詢"source"這個字串是否存在，就要判斷點陣圖中下標2，4，7對應的值是否均為1，若是，則說明此字串「可能」存在。注意這裡就可能出現誤判了（下面介紹）

布隆過濾器誤判

布隆過濾器是一個大型點陣圖（bit陣列或向量） + 多個無偏雜湊函數

如果我們要對映一個值到布隆過濾器中，我們需要使用多個不同的雜湊函數生成多個雜湊值，並對每個生成的雜湊值指向的 bit 位置 1，例如針對值 「source」 和三個不同的雜湊函數分別生成了雜湊值 2、4、7，則有下圖

現在，如果我們要查詢"source"這個字串是否存在，就要判斷點陣圖中下標2，4，7對應的值是否均為1，若是，則說明此字串「可能」存在。注意這裡就可能出現誤判了，至於為什麼我們先再存一個字串"create"，假設雜湊函數返回3，4，8，則對應的圖如下：

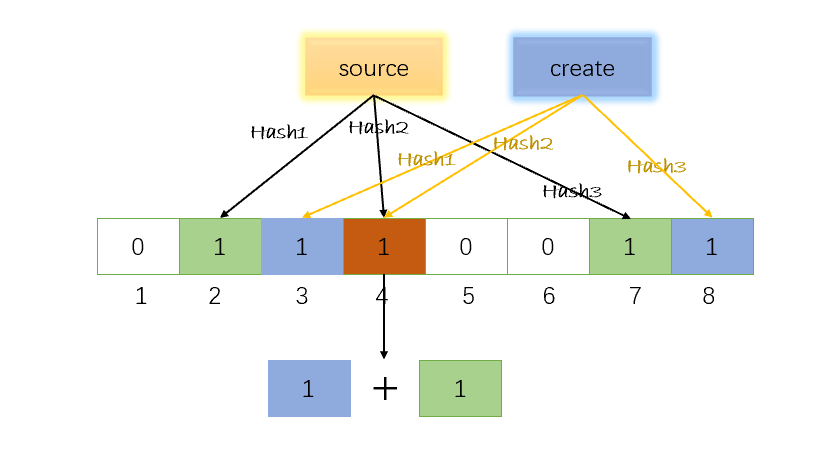
• 值得注意的是，4 這個 bit 位由於兩個值的雜湊函數都返回了這個 bit 位，因此它被覆蓋了。現在我們如果想查詢 「flower」 這個值是否存在，雜湊函數返回了 2、5、8三個值，結果我們發現 5 這個 bit 位上的值為 0，說明沒有任何一個值對映到這個 bit 位上，因此我們可以很確定地說 「flower」 這個值不存在。而當我們需要查詢 「source」 這個值是否存在的話，那麼雜湊函數必然會返回 2、4、7，然後我們檢查發現這三個 bit 位上的值均為 1，那麼我們可以說 「source」 存在了麼？答案是不可以，只能是 「source」 這個值可能存在（發生了誤判）。
• 這是為什麼呢？答案很簡單，因為隨著增加的值越來越多，被置為 1 的 bit 位也會越來越多，這樣某個值 「taobao」 即使沒有被儲存過，但是萬一雜湊函數返回的三個 bit 位都被其他值置位了 1 ，那麼程式還是會判斷 「taobao」 這個值存在。像上面的字串source，雜湊函數返回的是2，4，7，可是先前的字串create，雜湊函數返回的是3，4，8，你怎麼知道位元位4的值對應的是字串source呢？我說它是字串create的也沒毛病吧，因此「source」可能存在。這就是誤判出現的典型現象。

總結：布隆過濾器是無法解決誤判的問題的，一個key通過多種雜湊函數對映多個位元位只能說是降低誤判的概率，但無法去除。

布隆過濾器優缺點

優點：

• 增加和查詢元素的時間複雜度為:O(K), (K為雜湊函數的個數，一般比較小)，與資料量大小無關

• 雜湊函數相互之間沒有關係，方便硬體並行運算

• 布隆過濾器不需要儲存元素本身，在某些對保密要求比較嚴格的場合有很大優勢

• 在能夠承受一定的誤判時，布隆過濾器比其他資料結構有這很大的空間優勢

• 資料量很大時，布隆過濾器可以表示全集，其他資料結構不能

• 使用同一組雜湊函數的布隆過濾器可以進行交、並、差運算

缺點：

• 有誤判率，即存在假陽性(False Position)，即不能準確判斷元素是否在集合中(補救方法：再建立一個白名單，儲存可能會誤判的資料)
• 不能獲取元素本身
• 一般情況下不能從布隆過濾器中刪除元素
• 如果採用計數方式刪除，可能會存在計數迴繞問題

誤判控制

• 很顯然，過小的布隆過濾器很快所有的 bit 位均為 1，那麼查詢任何值都會返回「可能存在」，起不到過濾的目的了。布隆過濾器的長度會直接影響誤報率，布隆過濾器越長其誤報率越小。
• 另外，雜湊函數的個數也需要權衡，個數越多則布隆過濾器 bit 位置位 1 的速度越快，且布隆過濾器的效率越低；但是如果太少的話，那我們的誤報率會變高。

大佬在權衡過其中的關係後得出了一套比較得當的公式：

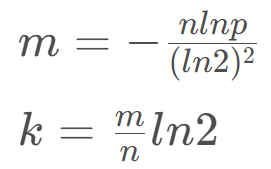
k 是雜湊函數個數
m 為布隆過濾器長度
n為插入的元素個數
p為誤判率

實現

整體框架

這裡用到了上一篇部落格中的點陣圖實現，其中這裡放置了3個雜湊函數，用了對映不同的概率。

在這裡完整程式碼bitset.h檔案

#pragma once
#include<iostream> //引入標頭檔案
#include<vector>
#include <string>
#include <new>
#include<algorithm> 
using namespace std; //標準名稱空間
class bitset
{
public:
	bitset(size_t bitCount)
		:bitCount(bitCount)
	{
		//resize會將vector中的元素初始化為0
		_bitset.resize(bitCount / 32 + 1);
	}
	// 每個位元組用0和1記錄某個數位存在狀態
	// 把x所在的資料在點陣圖的那一位變成1
	void set(int x)
	{
		if (x > bitCount) return;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是第index個整數的第pos個位

		_bitset[index] |= (1 << pos);
	}
	// 把x所在的資料在點陣圖的那一位變成0
	void reset(int x)
	{
		if (x > bitCount) return;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是滴index個整數的第pos個位
		_bitset[index] &= ~(1 << pos);
	}
	// 判斷x是否存在
	bool test(int x)
	{
		if (x > bitCount) return false;

		int index = x / 32;// x是第index個整數
		int pos = x % 32;// x是滴index個整數的第pos個位

		return _bitset[index] & (1 << pos);
	}

private:
	vector<int> _bitset;
	int bitCount;// 開num位元位的空間
};

雜湊函數個數和布隆過濾器長度的關係：

m = -n*ln(p) / (ln(2)^2)
k = m/n * ln(2)

k 是雜湊函數個數
m 為布隆過濾器長度
n為插入的元素個數
p為誤判率

其中k=3，整體算下來，m≈4.34n，所以這裡我們選擇m為5

template<class T = string, class Hash1 = BKDRHash, class Hash2 = SDBHash, class Hash3 = RSHash>
class BloomFilter
{
public:
	// 布隆過濾器的長度 近似等於4.3~5倍插入元素的個數
	// 這裡取 5
	BloomFilter(size_t size)
		:_bs(5 * size)
		, _N(5 * size)
	{}
private:
	bitset _bs;
	size_t _N;// 能夠對映元素個數 
};

三個字串雜湊函數如下： 用他們作為預設引數，預設處理字串型別

// BKDRHash
struct BKDRHash
{
	size_t operator()(const string& str)
	{
		register size_t hash = 0;
		for (size_t i = 0; i < str.length(); ++i)
		{
			hash = hash * 131 + str[i];
		}

		return hash;
	}
};

// SDBHash
struct SDBHash
{
	size_t operator()(const string str)
	{
		register size_t hash = 0;
		for (size_t i = 0; i < str.length(); ++i)
		{
			hash = 65599 * hash + str[i];
			//hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;  
		}
		return hash;
	}
};

// RSHash
struct RSHash
{
	size_t operator()(const string str)
	{
		register size_t hash = 0;
		size_t magic = 63689;
		for (size_t i = 0; i < str.length(); ++i)
		{
			hash = hash * magic + str[i];
			magic *= 378551;
		}
		return hash;
	}
};

插入

布隆過濾器的插入就是提供一個Set介面，核心思想就是把插入的元素通過三個雜湊函數獲取對應的整型並%位元位數從而獲得對應的3個對映位置，再把這三個位置置為1即可

步驟

1. 先用不同的雜湊函數計算出該資料分別要對映到點陣圖的哪幾個位置
2. 然後把點陣圖中的這幾個位置設定為1

void set(const T& x)
{
	size_t index1 = Hash1()(x) % _N;
	size_t index2 = Hash2()(x) % _N;
	size_t index3 = Hash3()(x) % _N;

	_bs.set(index1);
	_bs.set(index2);
	_bs.set(index3);
}

查詢

布隆過濾器的思想是將一個元素用多個雜湊函數對映到一個點陣圖中，因此被對映到的位置的位元位一定為

步驟：

• 先用不同的雜湊函數計算出該資料分別要對映到點陣圖的哪幾個位置

• 然後判斷點陣圖中的這幾個位置是否都為1，如果有一個不為1，說明該元素一定不在容器中，否則表示在容器中

注意： 可能會誤報，判斷在是不準確的，判斷不在是準確的。（因為一個資料判斷出它是在的，可能是它對映的幾個資料可能是其它資料對映導致這幾個位置為1的，所以判斷結果為在，該結果有誤判；而判斷一個資料為不在時，那這個資料是一定不在的，因為它對映的幾個位置不全為1）

bool IsInBloomFilter(const T& x)
{
	size_t index1 = Hash1()(x) % _N;
	size_t index2 = Hash2()(x) % _N;
	size_t index3 = Hash3()(x) % _N;

	return _bs.test(index1)
		&& _bs.test(index2)
		&& _bs.test(index3);// 可能會誤報，判斷在是不準確的，判斷不在是準確的
}

刪除

布隆過濾器不能直接支援刪除工作，因為在刪除一個元素時，可能會影響其他元素。

• 比如：刪除上圖中"create"元素，如果直接將該元素所對應的二進位制位元位置0，「source」元素也被刪除了，因為這兩個元素在多個雜湊函數計算出的位元位上剛好有重疊。

一種支援刪除的方法（計數法刪除）：

• 將布隆過濾器中的每個位元位擴充套件成一個小的計數器，插入元素時給k個計數器(k個雜湊函數計算出的雜湊地址)加一，刪除元素時，給k個計數器減一，通過多佔用幾倍儲存空間的代價來增加刪除操作。
• 缺陷：
  1. 無法確認元素是否真正在布隆過濾器中
  2. 存在計數迴繞

當然，為什麼至今過濾器都沒有提供對應的刪除介面呢？其實過濾器的本來目的就是為了提高效率和節省空間，但是在確認存在時去遍歷檔案，檔案 IO 和磁碟 IO 的時間開銷是不小的，其次在每個位元位增加額外的計數器，更是讓空間開銷飆升到本身的好幾倍。

完整程式碼以及測試

BloomFilter.cpp檔案

#define _CRT_SECURE_NO_WARNINGS
#include"bitset.h"
template<class T>
struct Hash
{
	const T& operator()(const T& key)
	{
		return key;
	}
};
// BKDRHash
struct BKDRHash
{
	size_t operator()(const string& str)
	{
		register size_t hash = 0;
		for (size_t i = 0; i < str.length(); ++i)
		{
			hash = hash * 131 + str[i];
		}

		return hash;
	}
};

// SDBHash
struct SDBHash
{
	size_t operator()(const string str)
	{
		register size_t hash = 0;
		for (size_t i = 0; i < str.length(); ++i)
		{
			hash = 65599 * hash + str[i];
			//hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;  
		}
		return hash;
	}
};

// RSHash
struct RSHash
{
	size_t operator()(const string str)
	{
		register size_t hash = 0;
		size_t magic = 63689;
		for (size_t i = 0; i < str.length(); ++i)
		{
			hash = hash * magic + str[i];
			magic *= 378551;
		}
		return hash;
	}
};
template<class T = string, class Hash1 = BKDRHash, class Hash2 = SDBHash, class Hash3 = RSHash>
class BloomFilter
{
public:
	// 布隆過濾器的長度 近似等於4.3~5倍插入元素的個數
	// 這裡取 5
	BloomFilter(size_t size)
		:_bs(5 * size)
		, _N(5 * size)
	{}
	void set(const T& x)
	{
		size_t index1 = Hash1()(x) % _N;
		size_t index2 = Hash2()(x) % _N;
		size_t index3 = Hash3()(x) % _N;

		_bs.set(index1);
		_bs.set(index2);
		_bs.set(index3);
	}
	bool IsInBloomFilter(const T& x)
	{
		size_t index1 = Hash1()(x) % _N;
		size_t index2 = Hash2()(x) % _N;
		size_t index3 = Hash3()(x) % _N;

		return _bs.test(index1)
			&& _bs.test(index2)
			&& _bs.test(index3);// 可能會誤報，判斷在是不準確的，判斷不在是準確的
	}


private:
	bitset _bs;
	size_t _N;// 能夠對映元素個數 
};
void TestBloomFilter()
{
	BloomFilter<string> bf(100);

	bf.set("douyin");
	bf.set("kuaishou");
	bf.set("pass cet6");
	bf.set("aabb");


	cout << bf.IsInBloomFilter("pass cet6") << endl;
	cout << bf.IsInBloomFilter("kuaishou") << endl;
	cout << bf.IsInBloomFilter("douyin") << endl;
	cout << bf.IsInBloomFilter("abab") << endl;
}

int main() {
	TestBloomFilter();
	system("pause");
	return EXIT_SUCCESS;
}

布隆過濾器優缺點

優點：

1. 增加和查詢元素的時間複雜度為:O(K)， (K為雜湊函數的個數，一般比較小)，與資料量大小無關
2. 雜湊函數相互之間沒有關係，方便硬體並行運算
3. 布隆過濾器不需要儲存元素本身，在某些對保密要求比較嚴格的場合有很大優勢
4. 在能夠承受一定的誤判時，布隆過濾器比其他資料結構有這很大的空間優勢
5. 資料量很大時，布隆過濾器可以表示全集，其他資料結構不能
6. 使用同一組雜湊函數的布隆過濾器可以進行交、並、差運算

缺點：

1. 有誤判率，即存在假陽性(False Position)，即不能準確判斷元素是否在集合中(補救方法：再建立一個白名單，儲存可能會誤判的資料)
2. 不能獲取元素本身
3. 一般情況下不能從布隆過濾器中刪除元素
4. 如果採用計數方式刪除，可能會存在計數迴繞問題

海量資料處理問題

雜湊切割

1. 給一個超過100G大小的log file, log中存著IP地址, 設計演演算法找到出現次數最多的IP地址？ 如何找到top K的IP？如何直接用Linux系統命令實現？

a. 先建立1000個小檔案A0-A999，然後計算i = hash(IP)%1000，i是多少，IP就進入編號為i的檔案中，也就是Ai檔案中，這樣相同的IP就都進入了同一個檔案中。先將一個小檔案載入到記憶體中，依次讀取放入unordered_map<string, int> 中，同時用一個pair<string, int> max記錄當前出現次數最多的IP，然後不斷更新記錄當前的max，這樣就得到出現次數最多的IP地址
b. 和上面的方法一樣，這裡用一個大小為K的堆來儲存topK的IP

點陣圖應用

1.給定100億個整數，設計演演算法找到只出現一次的整數？

100億個整數佔用40G的空間，如果直接載入到記憶體中，空間肯定是不夠的，所以我們這裡可以考慮用點陣圖來處理。
方案一： 改進點陣圖，用兩個位元位表示整數，用其中的三種狀態00（沒出現）、01（出現一次）和10（出現兩次及以上）。消耗記憶體為：2*4 *(2^32-1)/32 byte≈1G
方案二： 用兩個點陣圖同時操作，對應位元位無資料時，兩個點陣圖此處設為0，有一個資料時，將兩個點陣圖中一個設為0，一個設為1，有兩個及以上資料時，兩個點陣圖中對於位元位都設定為1。消耗空間和上面那種方法一樣，也是1G

2.給兩個檔案，分別有100億個整數，我們只有1G記憶體，如何找到兩個檔案交集？

方案一： 將檔案1的整數對映到一個點陣圖中，然後讀取檔案2中的資料，判斷是否在點陣圖中，在就是交集，消耗記憶體500M
方案二： 將檔案1的整數對映到一個點陣圖中， 將檔案2的整數對映到另一個點陣圖中，然後將兩個點陣圖進行按位元與，與之後點陣圖中為1的位就是兩個檔案的交集

3.點陣圖應用變形：1個檔案有100億個int，1G記憶體，設計演演算法找到出現次數不超過2次的所有整數

方案： 和第一題思路一致，找出狀態為00、01和10的即可，其中狀態為11代表的是出現3次及以上。消耗記憶體為1G

布隆過濾器

1.給兩個檔案，分別有100億個query，我們只有1G記憶體，如何找到兩個檔案交集？分別給出精確演演算法和近似演演算法

query是一個查詢語句的意思，一個query語句的大小平均約為30-60位元組100億個query大約佔用300-600G。
方案一（近似演演算法）： 將檔案1的query對映到布隆過濾器中，讀取檔案2中的query，判斷是否在布隆過濾器中，在就是交集，是交集的一定在裡面。（缺陷：交集中的數會不準確，因為有些數會誤判，混到交集裡面，判斷在是不準確的，判斷不在是準確的）
方案二（精確演演算法）：
1.把檔案1和檔案2分別切分成A0、A1…A999和B0、B1…B999，兩個檔案分別切分成1000個小檔案，然後將A0載入到記憶體放到unordered_set中，再依次和B0、B1…B999這10001個檔案進行比較，然後載入A1到記憶體中，以此類推。用unordered_set的效率還是很高的，基本上是常數次。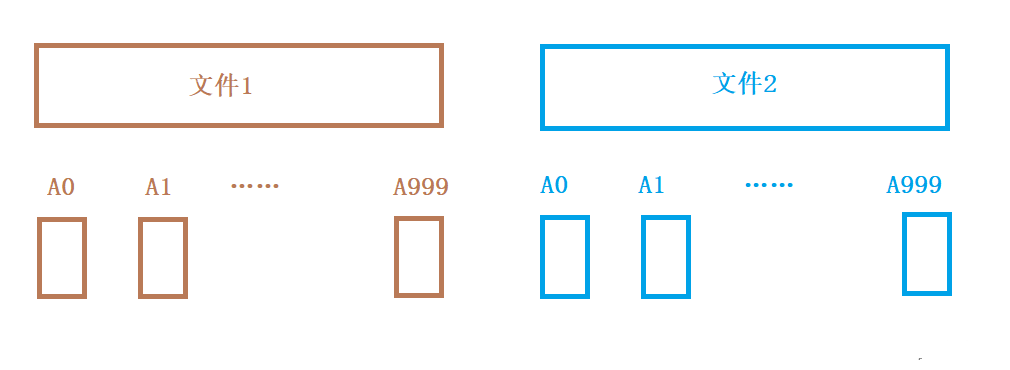

2.優化：雜湊切分
不再使用平均切分，使用雜湊切分，用公式：i = Hash(query)%1000。i是多少就進入編號為i的檔案中。不同的query可能會進入編號不同的檔案中，但相同的query一定會進入編號相同的檔案中。
先將檔案Ai載入到記憶體中，放到unordered_set中，然後讀取Bi中query，判斷是否在，在就是交集。這裡只需要比較1000次，比上面那種方式比較次數少很多。

2.如何擴充套件BloomFilter使得它支援刪除元素的操作

方案： 用幾個位元位來表示計數器。缺陷：給的為如果少了，容易導致計數溢位，如果位數多了，那麼空間開銷就會很多，是以犧牲布隆過濾器的優勢為代價的。