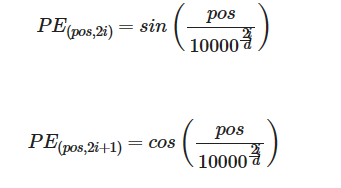深度學習之Transformer網路

【博主使用的python版本：3.6.8】

本次沒有額外的資料下載

Packages

ort tensorflow as tf
import pandas as pd
import time
import numpy as np
import matplotlib.pyplot as plt

from tensorflow.keras.layers import Embedding, MultiHeadAttention, Dense, Input, Dropout, LayerNormalization
from transformers import DistilBertTokenizerFast #, TFDistilBertModel
from transformers import TFDistilBertForTokenClassification
from tqdm import tqdm_notebook as tqdm

1 - 位置編碼

在順序到序列任務中，資料的相對順序對其含義非常重要。當你訓練順序神經網路（如RNN）時，你按順序將輸入輸入到網路中。有關資料順序的資訊會自動輸入到模型中。但是，在訓練轉換器網路時，會一次性將資料全部輸入到模型中。雖然這大大減少了訓練時間，但沒有關於資料順序的資訊。這就是位置編碼有用的地方 - 您可以專門編碼輸入的位置，並使用以下正弦和餘弦公式將它們傳遞到網路中：

d是詞嵌入和位置編碼的維度
pos是單詞的位置。
i指位置編碼的每個不同維度。

正弦和餘弦方程的值足夠小（介於 -1 和 1 之間），因此當您將位置編碼新增到單詞嵌入時，單詞嵌入不會明顯失真。位置編碼和單詞嵌入的總和最終是輸入到模型中的內容。結合使用這兩個方程有助於變壓器網路關注輸入資料的相對位置。請注意，雖然在講座中，Andrew 使用垂直向量，但在此作業中，所有向量都是水平的。所有矩陣乘法都應相應調整。

1.1 - 正弦角和餘弦角

通過計算正弦和餘弦方程的內項，獲取用於計算位置編碼的可能角度：

練習 1 - get_angles

實現函數 get_angles（）來計算正弦和餘弦位置編碼的可能角度

def get_angles(pos, i, d):
    """
    獲取位置編碼的角度
    
    Arguments:
        pos -- 包含位置的列向量[[0], [1], ...,[N-1]]
        i --   包含維度跨度的行向量 [[0, 1, 2, ..., M-1]]
        d(integer) -- 編碼大小
    
    Returns:
        angles -- (pos, d) 陣列
    """
    
    angles = pos/ (np.power(10000, (2 * (i//2)) / np.float32(d)))
    
    
    return angles

我們測試一下：

def get_angles_test(target):
    position = 4
    d_model = 16
    pos_m = np.arange(position)[:, np.newaxis]
    dims = np.arange(d_model)[np.newaxis, :]

    result = target(pos_m, dims, d_model)

    assert type(result) == np.ndarray, "你必須返回一系列陣列集合"
    assert result.shape == (position, d_model), f"防止錯誤我們希望: ({position}, {d_model})"
    assert np.sum(result[0, :]) == 0
    assert np.isclose(np.sum(result[:, 0]), position * (position - 1) / 2)
    even_cols =  result[:, 0::2]
    odd_cols = result[:,  1::2]
    assert np.all(even_cols == odd_cols), "奇數列和偶數列的子矩陣必須相等"
    limit = (position - 1) / np.power(10000,14.0/16.0)
    assert np.isclose(result[position - 1, d_model -1], limit ), f"組後的值必須是 {limit}"

    print("\033[92mAll tests passed")

get_angles_test(get_angles)

# 例如
position = 4
d_model = 8
pos_m = np.arange(position)[:, np.newaxis]
dims = np.arange(d_model)[np.newaxis, :]
get_angles(pos_m, dims, d_model)

All tests passed

Out[9]:

array([[0.e+00, 0.e+00, 0.e+00, 0.e+00, 0.e+00, 0.e+00, 0.e+00, 0.e+00],
       [1.e+00, 1.e+00, 1.e-01, 1.e-01, 1.e-02, 1.e-02, 1.e-03, 1.e-03],
       [2.e+00, 2.e+00, 2.e-01, 2.e-01, 2.e-02, 2.e-02, 2.e-03, 2.e-03],
       [3.e+00, 3.e+00, 3.e-01, 3.e-01, 3.e-02, 3.e-02, 3.e-03, 3.e-03]])

1.2 - 正弦和餘弦位置編碼

現在，您可以使用計算的角度來計算正弦和餘弦位置編碼。

練習 2 - 位置編碼

實現函數 positional_encoding（）來計算正弦和餘弦位置編碼

np.newaxis 有用，具體取決於您選擇的實現。就是將矩陣升維

def positional_encoding(positions, d):
    """
    預先計算包含所有位置編碼的矩陣
    
    Arguments:
        positions (int) -- 要編碼的最大位置數
        d (int) --編碼大小 
    
    Returns:
        pos_encoding -- (1, position, d_model)具有位置編碼的矩陣
    """
    # 初始化所有角度angle_rads矩陣
    angle_rads = get_angles(np.arange(positions)[:, np.newaxis],
                            np.arange(d)[ np.newaxis,:],
                            d)
  
    # -> angle_rads has dim (positions,d)
    # 將 sin 應用於陣列中的偶數索引;2i
    angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
  
    # a將 cos 應用於陣列中的偶數索引;2i; 2i+1
    angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
    # END CODE HERE
    
    pos_encoding = angle_rads[np.newaxis, ...]
    
    return tf.cast(pos_encoding, dtype=tf.float32)

我們來測試一下：

def positional_encoding_test(target):
    position = 8
    d_model = 16

    pos_encoding = target(position, d_model)
    sin_part = pos_encoding[:, :, 0::2]
    cos_part = pos_encoding[:, :, 1::2]

    assert tf.is_tensor(pos_encoding), "輸出不是一個張量"
    assert pos_encoding.shape == (1, position, d_model), f"防止錯誤，我們希望: (1, {position}, {d_model})"

    ones = sin_part ** 2  +  cos_part ** 2
    assert np.allclose(ones, np.ones((1, position, d_model // 2))), "平方和一定等於1 = sin(a)**2 + cos(a)**2"
    
    angs = np.arctan(sin_part / cos_part)
    angs[angs < 0] += np.pi
    angs[sin_part.numpy() < 0] += np.pi
    angs = angs % (2 * np.pi)
    
    pos_m = np.arange(position)[:, np.newaxis]
    dims = np.arange(d_model)[np.newaxis, :]

    trueAngs = get_angles(pos_m, dims, d_model)[:, 0::2] % (2 * np.pi)
    
    assert np.allclose(angs[0], trueAngs), "您是否分別將 sin 和 cos 應用於偶數和奇數部分？"
 
    print("\033[92mAll tests passed")

    
positional_encoding_test(positional_encoding)

All tests passed
計算位置編碼的工作很好！現在，您可以視覺化它們。

pos_encoding = positional_encoding(50, 512)

print (pos_encoding.shape)

plt.pcolormesh(pos_encoding[0], cmap='RdBu')
plt.xlabel('d')
plt.xlim((0, 512))
plt.ylabel('Position')
plt.colorbar()
plt.show()

(1, 50, 512)

每一行代表一個位置編碼 - 請注意，沒有一行是相同的！您已為每個單詞建立了唯一的位置編碼。

2 - 掩碼

構建transformer網路時，有兩種型別的掩碼很有用：填充掩碼和前瞻掩碼。兩者都有助於softmax計算為輸入句子中的單詞提供適當的權重。

2.1 - 填充掩碼

通常，輸入序列會超過網路可以處理的序列的最大長度。假設模型的最大長度為 5，則按以下序列饋送：

[["Do", "you", "know", "when", "Jane", "is", "going", "to", "visit", "Africa"], 
 ["Jane", "visits", "Africa", "in", "September" ],
 ["Exciting", "!"]
]
可能會被向量化為：

[[ 71, 121, 4, 56, 99, 2344, 345, 1284, 15],
 [ 56, 1285, 15, 181, 545],
 [ 87, 600]
]
將序列傳遞到轉換器模型中時，它們必須具有統一的長度。您可以通過用零填充序列並截斷超過模型最大長度的句子來實現此目的：

[[ 71, 121, 4, 56, 99],
 [ 2344, 345, 1284, 15, 0],
 [ 56, 1285, 15, 181, 545],
 [ 87, 600, 0, 0, 0],
]
長度超過最大長度 5 的序列將被截斷，零將被新增到截斷的序列中以實現一致的長度。同樣，對於短於最大長度的序列，它們也將新增零以進行填充。
但是，這些零會影響softmax計算 - 這是填充掩碼派上用場的時候！通過將填充掩碼乘以 -1e9 並將其新增到序列中，
您可以通過將零設定為接近負無窮大來遮蔽零。我們將為您實現這一點，以便您可以獲得構建transformer網路的樂趣！