子陣列的最大互斥或和問題

作者：Grey

原文地址：

部落格園：子陣列的最大互斥或和問題

CSDN：子陣列的最大互斥或和問題

題目描述

陣列中所有數都互斥或起來的結果，叫做互斥或和。給定一個陣列 arr，其中可能有正、有負，有零，返回 arr 的最大子陣列互斥或和

題目連結見：牛客-子陣列的最大互斥或和

暴力解

列舉每個子陣列的互斥或和，抓取全域性最大值返回，整個演演算法時間複雜度\(O(N^3)\)，整個過程比較簡單，不贅述，基於這個暴力解法，可以有優化一些的演演算法，就是利用字首互斥或和陣列，時間複雜度可以減少到\(O(N^2)\)，思路如下

第一步

申請一個和原始陣列一樣長的字首互斥或和陣列

int[] eor = new int[arr.length];

其中eor[i]表示原始陣列 0 位置到 i 位置的互斥或和是多少，實現程式碼如下：

    eor[0] = arr[0];
    for (int i = 1; i < n; i++) {
      eor[i] = eor[i - 1] ^ arr[i];
    }

有了 eor 陣列以後，對於任意 i 位置，0 到 i 區間的互斥或和就可以直接獲取到了，接下來是列舉陣列中任意兩個位置 i 和 j 區間的互斥或和，由於

i ~ j 之間的互斥或和等於 eor[j] ^ eor[i-1](i > 0)，所以

任何兩個位置之間的互斥或和資訊可以通過如下程式碼求得，其中 max 是全域性互斥或和的最大值

    for (int i = 1; i < n; i++) {
      max = Math.max(max, eor[i]);
      for (int j = i; j < n; j++) {
        max = Math.max(max, eor[j] ^ eor[i - 1]);
      }
    }

完整程式碼如下

  public static int maxEor1(int[] arr, int n) {
    int[] eor = new int[arr.length];
    int max = arr[0];
    eor[0] = arr[0];
    for (int i = 1; i < n; i++) {
      eor[i] = eor[i - 1] ^ arr[i];
    }
    for (int i = 1; i < n; i++) {
      max = Math.max(max, eor[i]);
      for (int j = i; j < n; j++) {
        max = Math.max(max, eor[j] ^ eor[i - 1]);
      }
    }
    return max;
  }

整個演演算法複雜度是\(O(N^2)\)，並不是最優解。

最優解

根據上述暴力解法，時間複雜度比較高的部分是：

當確定了 0 ~ i 位置的互斥或和以後，如何定位 0 ~ j 這個區間，使得 j ~ i 之間的互斥或和最大。

暴力解法使用的是遍歷的方式，而最優解，可以使用字首樹進行加速匹配，關於字首樹的內容，可以參考：字首樹的設計和實現

以陣列[11,1,15,10,13,4]為例，我們把其字首互斥或和陣列轉換成二進位制，結果如下(其中eor[i..j]表示i~j的互斥或和)

eor[0..0] = 1011

eor[0..1] = 1010

eor[0..2] = 0101

eor[0..3] = 1111

eor[0..4] = 0010

eor[0..5] = 0110

把這些字首互斥或和加入字首樹,

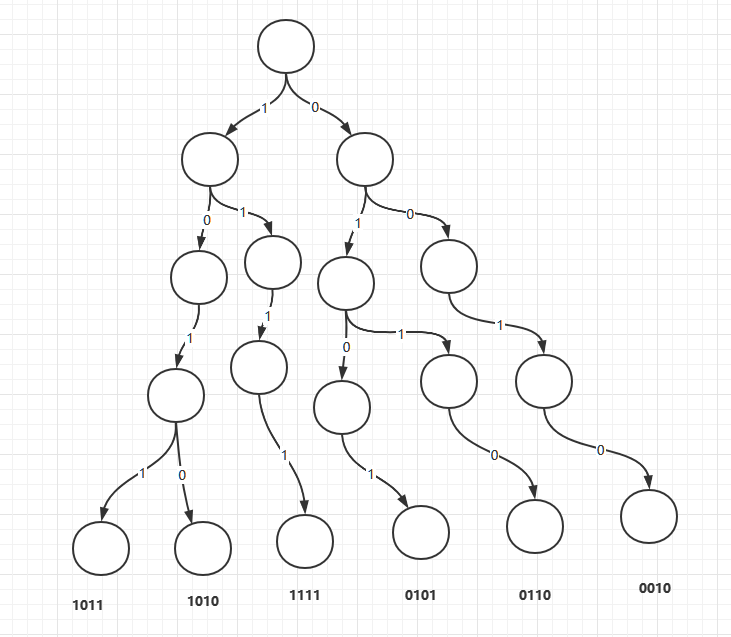
接下來，對於任何一個eor[i](0~i的互斥或和)來說，進入字首樹以後，字首樹需要快速找到和其匹配的eor[j]，使得i~j之間的互斥或和最大，規則就是最高位（符號位）期待一樣，緊著高位要期待不一樣的值

例如：

eor[2] = 0101

eor[2] 期待和它符號位一樣為0的值，緊著高位（由於前面28都是0，所以不存在和它符號不一樣的，只看最後4位元，

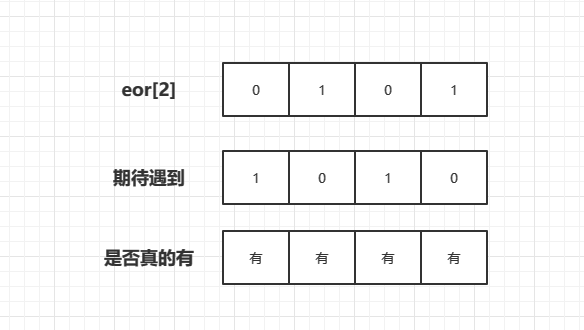
通過這個貪心，就可以在\(O(1)\)時間複雜度直接得到結果。

說明：如果期待遇到 0 可是字首樹沒有往 0 方向的路，那直接返回 1 即可，反之亦然。

完整程式碼如下

  public static int maxEor(int[] arr, int n) {
    int[] eor = new int[arr.length];
    int max = 0;
    eor[0] = arr[0];
    for (int i = 1; i < n; i++) {
      eor[i] = eor[i - 1] ^ arr[i];
    }
    Trie trie = new Trie(eor);
    trie.add(eor[0]);
    for (int i = 1; i < n; i++) {
      max = Math.max(max, trie.get(eor[i]));
    }
    return max;
  }

  public static class Trie {
    public Node head;

    public Trie(int[] arr) {
      head = new Node();
      for (int eor : arr) {
        add(eor);
      }
    }

    public void add(int num) {
      Node cur = head;
      for (int bit = 31; bit >= 0; bit--) {
        int i = ((num >>> bit) & 1);
        if (cur.next[i] == null) {
          cur.next[i] = new Node();
        }
        cur = cur.next[i];
      }
    }

    public int get(int eor) {
      int expect = 0;
      Node cur = head;
      for (int bit = 31; bit >= 0; bit--) {
        // 符號位期待一樣的
        // 非符號位期待相反的
        int expectBit = bit == 31 ? ((eor >>> bit) & 1) : (eor >>> bit & 1 ^ 1);
        if (cur.next[expectBit] != null) {
          expect = ((expectBit << bit) | expect);
          cur = cur.next[expectBit];
        } else {
          expectBit = (expectBit ^ 1);
          cur = cur.next[expectBit];
          expect = ((expectBit << bit) | expect);
        }
      }
      return expect ^ eor;
    }
  }

  public static class Node {
    public Node[] next = new Node[2];
  }

整個演演算法時間複雜度\(O(N)\)，最優解。

更多

演演算法和資料結構筆記