【機器學習】李宏毅——Domain Adaptation(領域自適應)

在前面介紹的模型中，一般我們都會假設訓練資料和測試資料符合相同的分佈，這樣模型才能夠有較好的效果。而如果訓練資料和測試資料是來自於不同的分佈，這樣就會讓模型在測試集上的效果很差，這種問題稱為Domain shift。那麼對於這種兩者分佈不一致的情況，稱訓練的資料來自於Source Domain，測試的資料來自於Target Domain。

那麼對於領域轉變的問題，具體的做法隨著我們對於目標領域的瞭解程度不同而不同，主要有以下幾種情況：

• 我們當前擁有少量目標領域的樣本且含有標註：具體做法是取其中的一小部分去「微調」訓練好的模型，但要注意不能夠訓練太多次迭代否則可能會對小部分的樣本產生過擬合
• 我們擁有目標領域的大量資料但是沒有標註
• 我們擁有很少量的目標領域的資料且沒有標註
• 我們根據對於目標領域沒有認識與瞭解

那我們關注的主要是第二種情況，它是我們現實生活中的常見情況。那麼最基本的想法是我們能不能訓練一個特徵提取器，它可以接受訓練集和測試集的樣本，然後輸出是對這些樣本的關鍵特徵進行提取，例如下圖的例子中就是去除掉顏色的影響，提取它作為數位最關鍵的特徵。

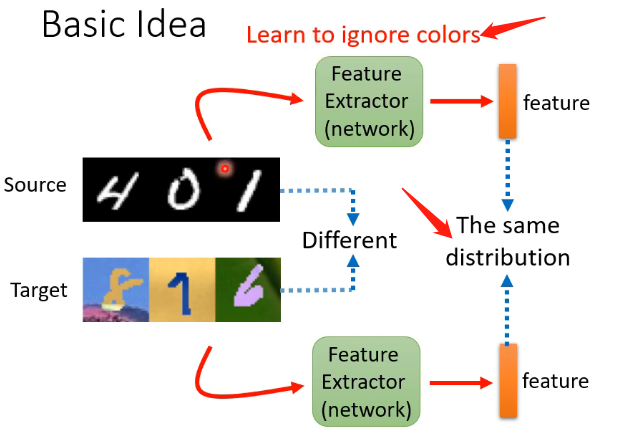
Domain Adversarial Training

這個想法是基於上面說的基本想法之上，但是它沒有專門地去訓練一個特徵提取器，它只是在原來的模型上，劃分一部分為特徵提取器，另一部分為標籤預測器，如下圖：

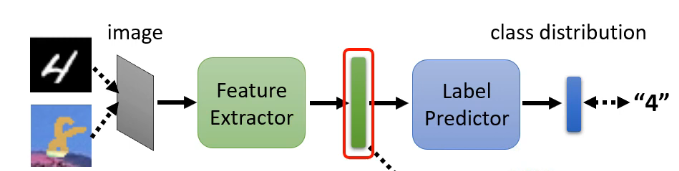
那麼在這個模型中，如果輸入的是訓練集的圖片，我們可以通過其輸出結果與真實結果之間的交叉熵來進行訓練，但是如果輸入是測試集的圖片，由於沒有標籤就無法來調整引數，但這時就要想到我們的特徵提取器。

經過特徵提取器處理之後得到的向量，我們是希望訓練集得到的向量分佈，和測試集得到的向量分佈是沒有差異的，如下圖：

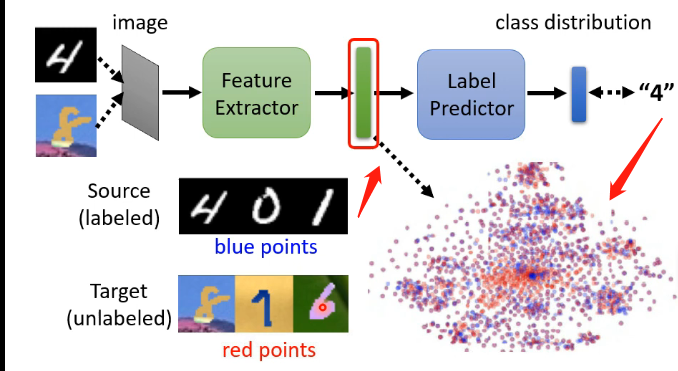
那麼怎麼讓這兩個分佈之間越接近越好呢？這時候就想到了對抗的思想，我們可以加入一個領域分辨器，它的輸入就是特徵提取器的這個輸出向量，而輸出就是該向量是來自於訓練集還是測試集，因此我們可以將特徵提取器看成是生成器，將領域分辨器看成是辨認器，特徵提取器是不斷調整引數來騙過領域分辨器，而領域分辨器則不斷學會來區分，如下圖：

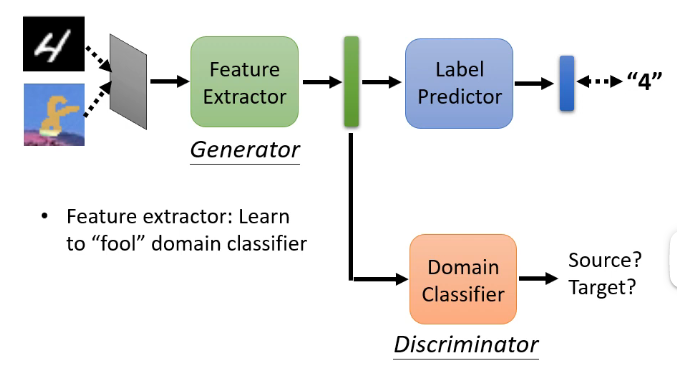
但是我們要考慮到一個問題：有沒有可能這樣會使得特徵提取器學習到不管我得到什麼樣的輸入，我都輸出一模一樣的向量（例如零向量）這樣你肯定無法分辨？可能會存在這個問題，但是如果真的只生成一模一樣的向量，那麼後面的標籤預測器也就無法做出預測了！因此我們可以通過標籤預測器的輸出來防止這種情況的發生！

假設特徵提取器的引數為\(\theta_f\)，標籤預測器的引數為\(\theta_p\)，領域辨別器的引數為\(\theta_d\)，而L為標籤預測器預測結果與真實結果之間交叉熵算出來的損失函數，\(L_d\)為領域辨別器分辨的時候的損失函數，那麼各自的訓練目標為：

第三個公式表明特徵提取器一方面是希望能夠降低後面預測的誤差，另一方面是為了讓領域辨別器無法分辨，從而來使得兩個分佈更加接近。

Limitation

假設我們當前樣本的類別有兩類，那麼對於有標籤的訓練集我們可以明顯地劃分為兩類，那麼對於沒有標籤的測試我們希望它的分佈能夠和訓練集的分佈越接近越好，如下圖的右圖：

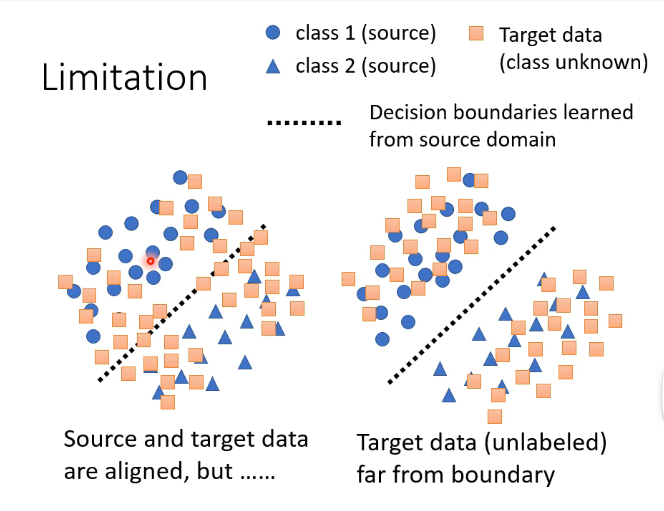
那麼在這個思路上進行拓展的話，對於我們剛才手寫識別的例子，我們輸入一張圖片得到的是一個向量，其中含有屬於每一個分類的概率，那我們希望的是這個測試集的樣本離分界線越遠越好，那就代表它得到的輸出向量要更加集中於某一類的概率，不能夠各個分類的可能性都差不多，即：

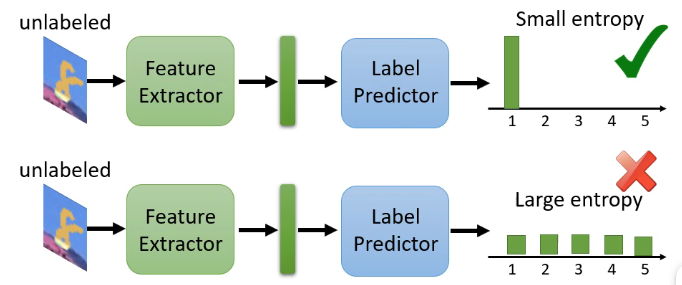
那麼上述想法的問題在於，有沒有可能訓練集和測試集的分類根據就是不同的呢？例如訓練集中可以分為老虎和獅子兩類，而測試集還有另外的狼呢？如下圖：

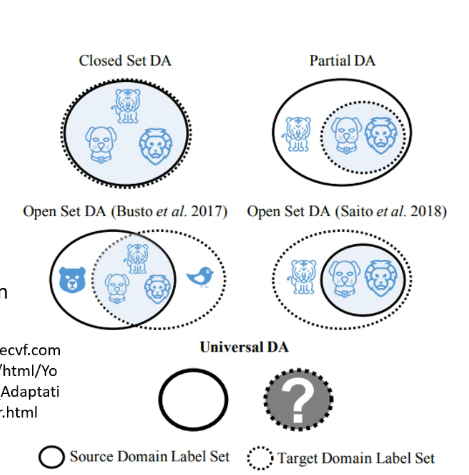
那麼這也是一個值得研究的問題。

其他情況

除了上述介紹的情況，我們對於測試集的瞭解程度還有其他的情況，例如我們只擁有很少量的測試集並且還沒有標籤，甚至於說我們對於測試集什麼都不知道。這些情形會更加的複雜，目前也仍然處於研究之中