C++進階(map+set容器模擬實現)
關聯式容器
關聯式容器也是用來儲存資料的,與序列式容器(如vector、list等)不同的是,其裡面儲存的是<key,value>結構的鍵值對,在資料檢索時比序列式容器效率更高。今天要介紹的的四種容器是樹形關聯式容器:map、set、multimap和multiset。它們的底層都是用紅黑樹來實現的,容器中的元素是一個有序的序列。
匿名物件
概念:匿名物件可以理解為是一個臨時物件,一般系統自動生成的
匿名物件的生命週期
- Cat(); ---> 生成了一個匿名物件,執行完Cat( )程式碼後,此匿名物件就此消失。這就是匿名物件的生命週期。
- Cat cc = Cat(); --->當發現匿名物件初始化一個新物件時,會直接把這個匿名物件轉成新物件,首先生成了一個匿名物件,然後將此匿名物件變為了cc物件,其生命週期就變成了cc物件的生命週期
注意匿名物件的賦值(=)操作含義是不一樣的:
//觀察這兩個語句
A.Cat cc = cat();
B.Cat cc2 = cc;
A中=是一個初始化操作,表示初始化一個匿名物件,只會呼叫一次建構函式,然後將匿名物件進行型別轉換轉化成有名物件cc,注意是Cat()匿名物件呼叫的建構函式,轉化為有名物件cc之後,cc的生命週期就是匿名物件的生命週期
B中的=就是賦值操作,也就是呼叫拷貝構造,深淺拷貝問題,要注意區分
例子1:我們來看看,匿名物件賦值的幾種情況
class A
{
public:
A(int s)
{
cout << "呼叫有參構造" << endl;
i = s;
}
A(const A& a)
{
cout << "呼叫拷貝構造" << endl;
}
~A()
{
cout << "呼叫解構函式" << endl;
}
void show()
{
cout << this->i << endl;
}
private:
int i;
};
void playstage()
{
//1.此處發生隱身轉換。。。。相當於 A a = A(11); 此處的A(11)就是一個匿名物件
/*
輸出結果:呼叫有參構造
呼叫解構函式
分析:首先此時A(11)是一個匿名物件,呼叫了有參建構函式,這時將匿名物件進行型別轉化轉化成a,此時匿名物件就是a,生命週期和a相同
*/
A a = 11;
//2.當匿名物件有等待初始化的物件接的時候,只呼叫一次構造和解構函式,和上面的情況差不多
A b = A(12);
//3.當匿名物件有已經初始化的物件接的時候
A c(12);
//此處為賦值,此處的匿名物件會呼叫一次建構函式
/*
輸出結果:呼叫有參構造
呼叫有參構造
呼叫解構函式
13
呼叫解構函式
分析:首先這就不是一個普通的初始化匿名物件了,因為匿名物件賦值的是一個已經初始化的物件,首先A c(12);會呼叫有參構造,其次A(13)會呼叫有參構造,此時的(=)是一個賦值的操作,但是不會呼叫拷貝構造,當A(13)執行完程式碼之後,呼叫解構,結束匿名物件的生命週期,此時匿名物件的值賦值給物件c,隨後c呼叫解構,結束程式
總結:所以當匿名物件賦值給一個已經初始化的物件的時候,匿名物件在執行完函數體後就會自動釋放,這時候不是普通的賦值,是一種特殊的賦值,不會呼叫拷貝建構函式,但是會將匿名物件內成員變數的值賦值給有名物件
*/
c = A(13);
c.show();
}
例子2:看看匿名物件的生命週期
class Cat
{
public:
Cat()
{
cout<<"Cat類 無參建構函式"<<endl;
}
Cat(Cat& obj)
{
cout<<"Cat類 拷貝建構函式"<<endl;
}
~Cat()
{
cout<<"Cat類 解構函式 "<<endl;
}
};
void playStage() //一個舞臺,展示物件的生命週期
{
Cat(); /*在執行此程式碼時,利用無參建構函式生成了一個匿名Cat類物件;執行完此行程式碼,
因為外部沒有接此匿名物件的變數,此匿名又被解構了*/
Cat cc = Cat(); /*在執行此程式碼時,利用無參建構函式生成了一個匿名Cat類物件;然後將此匿名變 成了cc這個範例物件*/
}
int main()
{
playStage();
system("pause");
return 0;
}
產生匿名物件的三種情況
-
以值的方式給函數傳參
-
型別轉換
-
函數需要返回一個物件
我們來看一個例子:在程式碼中給出了執行結果和解釋,小夥伴們可以賦值程式碼到編譯器中自己執行偵錯一下看看具體的過程
#define _CRT_SECURE_NO_WARNINGS
#include<iostream> //引入標頭檔案
#include<algorithm>
using namespace std; //標準名稱空間
//鍵值對的定義
template <class T1, class T2>
struct pair
{
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair() :first(T1()), second(T2()) {}
pair(const T1& a, const T2& b) :first(a),second(b){}
};
//匿名物件產生的三種情況
class Maker
{
public:
Maker()
{
cout << "呼叫無參建構函式" << endl;
this->a = 0;
}
Maker(int a)
{
cout << "呼叫有參建構函式" << endl;
this->a = a;
}
Maker(const Maker& maker)
{
cout << "呼叫拷貝建構函式" << endl;
this->a = maker.a;
}
Maker Makertest1()
{
//執行 return *this; 會產生一個匿名物件,作為返回值
//本質:Maker 匿名物件名 = *this;
//強調一下:如果返回值是參照,則不會產生匿名物件,因為返回的其實是地址,給地址取別名,和物件無關
return *this;
}
Maker Makertest2()
{
//執行 return temp;會先產生一個匿名物件,執行拷貝建構函式,作為返回值,
// 本質:Maker 匿名物件名 = maker1;
//然後釋放臨時物件temp
Maker temp(2);
return temp;
}
//總結:函數返回值為一個物件(非參照)的時候會產生一個匿名物件,匿名物件根據主函數的操作決定生命週期
Maker& Makertest3()
{
//執行 return temp;不會產生匿名物件,而是會將temp的地址先賦值到參照中,
//在釋放temp的記憶體,此時Point&得到是一個髒資料,是非法的,因為temp在函數結束的時候被釋放了,此時地址非法
Maker temp(3);
return temp;
}
~Maker()
{
cout << "呼叫解構函式" << endl;
this->a = 0;
}
private:
int a;
};
//1.以值的方式給函數傳參
/*
讓我們看看本質:
輸出結果:呼叫無參建構函式
呼叫拷貝建構函式
呼叫解構函式
呼叫解構函式
為什麼會有這樣的結果呢?首先main函數呼叫test01,進入函數體,呼叫Maker m1;會呼叫無參建構函式,然後
呼叫func函數,在func函數傳參的過程中發生了Maker m = m1;會呼叫拷貝構造,然後func函數結束,m呼叫解構,test01結束,m1呼叫解構
我們看到了呼叫了拷貝建構函式,在傳參的時候建立了臨時物件m;對m的修改不會影響原來物件,這是第一種產生臨時物件的情況,所以我們傳參的時候儘量傳入物件的參照
*/
void func(Maker m)//本質 Maker m = m1;
{
}
void test01()
{
Maker m1;
func(m1);
}
//2.型別轉換,生成臨時物件
/*
讓我們看看本質:
輸出結果:
呼叫無參建構函式
呼叫解構函式
為什麼會出現這種結果呢?因為用做型別轉換的時候,實際上呼叫的是Maker()這個匿名物件的建構函式,
此時匿名物件會直接轉換成新物件maker2,此時Maker()的生命週期就是maker2的生命週期
*/
void test02()
{
//生成一個匿名物件,因為用來初始化同型別的物件,這個匿名物件會直接轉化成新物件,減少資源消耗
Maker maker2 = Maker();
}
//3.函數需要返回一個物件
void test3()
{
/*
測試1:Makertest1()
執行結果:呼叫有參建構函式
呼叫拷貝建構函式
呼叫解構函式
呼叫函數
分析:首先呼叫Maker(2)建立匿名物件,呼叫有參構造,這時候=不是賦值,而是初始化匿名物件,這一點要注意,其次呼叫函數Makertest1(),函數的返回值return *this;此時會發生拷貝構造 Maker 匿名物件 = *this;
匿名物件呼叫拷貝構造拷貝this中的內容,所以此時會輸出呼叫拷貝建構函式,函數Makertest1()返回的是一個匿名物件,所以Maker m1 = Maker(2).Makertest1()本質上就是Maker m1 = 匿名物件,注意此時的匿名物件是新生成的
而不是原來的Maker(2),所以原來的Maker(2)在執行完函數之後會呼叫解構函式,賦值給Maker m1不是原來的Maker(2)的那個匿名物件,而是一個新的匿名物件,新的匿名物件和m1繫結在一起,生命週期一致
*/
//Maker m1 = Maker(2).Makertest1();
/*
測試2:Makertest2()
執行結果:呼叫有參構造
呼叫有參構造
呼叫拷貝建構函式
解構
解構
解構
分析:首先呼叫Maker(2)呼叫有參構造,初始化匿名物件,隨後呼叫Makertest2()函數,進入函數體內,又建立了一個物件tmp,所以又呼叫了一次有參構造,當把物件return的時候,發生了Maker 匿名物件 = tmp,所以呼叫了拷貝構造,此時重新生成了一個匿名物件,當函數Makertest2()結束的時候tmp解構,當Maker(2).Makertest2()執行完畢,匿名物件Maker(2)解構,當test03結束,m2解構
*/
//Maker m2 = Maker(2).Makertest2();
/*
測試3:Makertest3()
執行結果:呼叫有參構造
呼叫有參構造
解構
呼叫拷貝構造
解構
解構
分析:首先呼叫Maker(2)呼叫有參構造,初始化匿名物件,隨後呼叫Makertest3()函數,進入函數體,函數體內建立了一個物件tmp,所以又呼叫了一次有參構造,此時return tmp,返回的是參照:Maker &a = tmp;此時a是一個真實的物件,而不是匿名物件,因為是對tmp物件的參照,此時函數Makertest3()函數執行完畢,tmp作為區域性變數被釋放,呼叫了解構,此時Maker(2).Makertest3()返回了物件a,Maker m3 = Maker(2).Makertest3()-->Maker m3 = a;所以呼叫了拷貝構造,Maker(2).Makertest3()執行完畢之後,Maker(2)始終都是匿名物件,Maker(2).Makertest3()執行完畢之後,Maker(2)生命週期走到了盡頭,呼叫解構,test3執行完畢,m3呼叫解構
*/
Maker m3 = Maker(2).Makertest3();
cout << "hh" << endl;
}
int main() {
//test01();
//test02();
test3();
system("pause");
}
鍵值對
鍵值對: 用來表示具有一一對應關係的一種結構,該結構中一般只包含兩個成員變數key和value,key代表鍵值,value表示與key對應的資訊
鍵值對的定義
STL中鍵值對定義如下:
//鍵值對的定義
template <class T1, class T2>
struct pair
{
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair() :first(T1()), second(T2()) {}
pair(const T1& a, const T2& b) :first(a), second(b){}
};
鍵值對建立
方法一: pair<T1, T2>(x, y) 使用建構函式的方式構造一個匿名物件
方法二: make_pair(x, y) 是一個函數模板,其中返回的是一個pair的匿名物件
//函數模板
template <class T1, class T2>
pair<T1, T2> make_pair(T1 x, T2 y)
{
return (pair<T1, T2>(x, y));
}
舉個例子:
void test()
{
// pair<T1, T2>(T1(), T2()) 通過建構函式構造一個匿名物件
// make_pair(T1() , T2()) 是一個模板函數,返回的是pair的匿名物件,用起來更方便
pair<int, int>(1, 1);
make_pair(1, 1);
}
set
概述
- set容器時關聯式容器,容器自身有規則,通過鍵值(key)排序,set不像map那樣,同時擁有key和value(pair),set的元素既是鍵值也是實值,set不允許兩個元素有兩個元素有相同的鍵值
- set容器和multiset容器的區別就是multiset允許有相同的元素,而在set容器中不允許相同元素的實現
- 在set中,元素的value也標識它(value就是key,型別為T),並且每個value必須是唯一的。set中的元素不能在容器中修改(元素總是const),但是可以從容器中插入或刪除它們
- 資料結構:二元搜尋樹
- 迭代器:雙向迭代器
- 常用api:
- 構造
- 賦值
- 大小
- 插入和刪除
- 查詢
- 改變規則:預設是從小到大,改變規則,加入謂詞到<>第二個引數中
- 注意:
- set容器插入相同元素的時候,不會報錯,但是不插入資料
- set容器儲存物件的時候,需要告訴set容器的規則
set中常用的介面
建構函式
set<T> st;//set預設的建構函式,構造空的set容器
set(const set& st);//拷貝建構函式
大小和容量
size();//返回容器中元素的數目
empty();//判斷容器是否為空
插入和刪除
pair<iterator,bool> insert(const value_type& val);//插入元素,返回值是鍵值對,其中如果第二個引數為true,那麼第一個引數是插入元素的迭代器的位置,為false的話,第一個引數就是已經存在元素的迭代器的位置
clear();//清除所有元素
erase(iterator position);//刪除pos迭代器所指的元素,返回下一個元素的迭代器
erase(begin,end);//刪除區間[begin,end)的所有元素,返回下一個元素的迭代器
erase(elem);//刪除容器中值為elem的元素
查詢
這裡只介紹find一個,find 查詢某個元素。這裡find的時間複雜度為O(logN),比演演算法中的find(時間複雜是O(N))更高效,所以set容器一般使用自己的find進行查詢
iterator find(const value_type& val) const;//查詢鍵val是否存在,若存在,返回該鍵的元素的迭代器;若不存在,返回set.end()
1.count(key);//查詢鍵key的元素個數
2.lower_bound(keyElem);//返回第一個key>=keyElem元素的迭代器。
3.upper_bound(keyElem);//返回第一個key>keyElem元素的迭代器。
equal_range(keyElem);//返回容器中key與keyElem相等的上下限的兩個迭代器
範例演示1:插入、刪除、查詢和迭代器遍歷
void test_set1()
{
set<int> s;
s.insert(5);
s.insert(1);
s.insert(6);
s.insert(3);
s.insert(6);
s.insert(s.begin(), 10);
set<int>::iterator pos = s.find(15);// 底層是搜尋二元樹,時間複雜度是O(logN)
// set<int>::iterator pos = find(s.begin(), s.end(), 3);// 遍歷查詢,時間複雜度是O(N)
if (pos != s.end())
{
// cout << *pos << endl;
s.erase(pos);// 沒有會報錯
}
//s.erase(1); // 沒找到不會報錯
set<int>::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
for (auto e : s)
{
cout << e << " ";
}
cout << endl;
}
執行結果如下:

範例演示2:演演算法中的find和set中的find進行效率比較
void test_set2()
{
srand((size_t)time(nullptr));
set<int> s;
for (size_t i = 0; i < 10000; ++i)
{
s.insert(rand());
}
cout << "個數:" << s.size() << endl;
int begin1 = clock();
for (auto e : s)
{
s.find(e);
}
int end1 = clock();
int begin2 = clock();
for (auto e : s)
{
find(s.begin(), s.end(), e);
}
int end2 = clock();
cout << "用時1:" << end1 - begin1 << "ms" << endl;
cout << "用時2:" << end2 - begin2 << "ms" << endl;
}
執行結果如下:

map
概述
- map是關聯容器,它按照特定的次序(按照key來比較)儲存由鍵值key和值value組合而成的元素,也就是說map所有的元素都是pair,pair第一個元素被視為key值,第二個value值,map中不允許兩個元素有相同的key值
- 在內部,map中的元素總是按照鍵值key進行比較排序的
- map支援下標存取符,支援operator[],即在[]中放入key,就可以找到與key對應的value
- 我們可以通過map迭代器改變map的鍵值嗎?答案是不可以的,因為map的鍵值關係到map元素的排序規則,任意改變map值將會嚴重破壞map組織,如果想要修改value值,當然是可以的
- 資料結構:平衡二元搜尋樹(紅黑樹)
- map和multimap容器的區別是multimap允許有相同元素
- 常用的api:
- 建構函式
- 賦值
- 大小
- 查詢
- 插入
- 刪除
map常用的介面
建構函式
map<T1,T2> mapTT;//map預設建構函式,構造一個空的map容器
map(const map& mp);//拷貝建構函式
大小和容量
size();//返回容器中元素的數目
empty();//判斷容器是否為空
插入和刪除
pair<iterator,bool> insert (const value_type& x );//返回的是一個鍵值對,插入元素,其中如果第二個引數為true,那麼第一個引數是插入元素的迭代器的位置,為false的話,第一個引數就是已經存在元素的迭代器的位置
map<int,string> mapStu;
// 第一種通過pair的方式插入物件
mapStu.insert(pair<int,string>(3, "小張"));
// 第二種通過
pair的方式插入物件mapStu.inset(make_pair(-1, "校長"));
// 第三種通過
value_type的方式插入物件mapStu.insert(map<int,string>::value_type(1,"小李"));
// 第四種通過陣列的方式插入值
mapStu[3] = "小劉";
mapStu[5] = "小王";
clear();//刪除所有元素
erase(iterator position);//刪除pos迭代器所指的元素,返回下一個元素的迭代器
erase(begin,end);//刪除區間[begin,end)的所有元素,返回下一個元素的迭代器
erase(elem);//刪除容器中值為elem的元素
查詢
find(key);//查詢鍵key是否存在,若存在,返回該鍵的元素的迭代器;若不存在,返回map.end()
count(keyElem);//返回容器中key為keyElem的對組個數,對map來說,要麼是0,要麼是1;對multimap來說,值可能大於1
lower_bound(keyElem);//返回第一個key>=keyElem元素的迭代器
upper_bound(keyElem);//返回第一個key>keyElem元素的迭代器
equal_range(keyElem);//返回容器中key與keyElem相等的上下限的兩個迭代器
operator[] (重點)
operator[]函數的定義如下
mapped_type& operator[] (const key_type& k)
{
return (*((this->insert(make_pair(k,mapped_type()))).first)).second;
}
//通俗點介紹[]的功能,[]在底層其實是一個insert操作,而上面介紹過,insert返回的pair<iterator,bool>,如果插入成功,那麼第一個引數就是插入元素迭代器的位置,如果插入失敗,那麼第一個引數就是已經存在元素的迭代器的位置,所以(*((this>insert(make_pair(k,mapped_type()))).first)).second簡化一下就是( *(pair <iterator,bool> .first)).second,pair <iterator,bool>.first代表取出pair中的迭代器iterator,(*(pair <iterator,bool> .first)).second簡化一下就是(*iterator).second,而 *iterator指向的又是一個pair元素,也就是鍵為k的那個迭代器,取這個pair的second,也就是value值,返回這個value值的參照,返回參照就可以對value值實現直接的修改和存取,這樣大家應該就理解了這麼一大段程式碼是什麼意思了吧
其中,mapped_type是KV模型中V的型別,也就是返回value值的參照。我們可以對這個value進行修改。
分析:((this->insert(make_pair(k,mapped_type()))).first這是一個迭代器,迭代器指向鍵值對中的第二個元素就是value。所以operato[]的底層是用到了插入,同時可以對value進行修改和存取。
總結: operator[]的三個用處:插入、修改和存取
範例演示:
範例1 用map統計水果個數,以下用了3種方式,同時還對operator的幾種作用進行了說明
void test_map2()
{
map<string, int> Map;
string fruitArray[] = { "西瓜","桃子","香蕉","桃子","蘋果","西瓜", "香蕉","蘋果", "香蕉","西瓜","桃子", "西瓜", "西瓜","桃子",
"桃子", "桃子", "西瓜","桃子","香蕉","桃子","蘋果","西瓜" };
//方法一
for (auto& e : fruitArray)
{
map<string, int>::iterator ret = Map.find(e);
//判斷是否找到了
if (ret != Map.end())
{
//注意此時迭代器指向的是pair元素
//找到了,說明容器裡有,第二個引數加1即可
++ret->second;
}
else
{
//沒有就插入,第二個引數記作1
Map.insert(make_pair(e, 1));
}
}
//方法二
for (auto& e : fruitArray)
{
// Map無此元素,pair的第一個引數返回新的迭代器,第二個引數返回true
// Map有此元素,pair的第一個引數返回舊的迭代器,第二個引數返回false
pair<map<string, int>::iterator, bool> ret = Map.insert(make_pair(e, 1));
// 插入失敗,只需要++value即可
if (ret.second == false)
{
++ret.first->second;
}
}
// 方法三
for (auto& e : fruitArray)
{
// mapped_type& operator[] (const key_type& k) ;
// mapped_type& operator[] (const key_type& k) { return (*((this->insert(make_pair(k,mapped_type()))).first)).second; }
// ((this->insert(make_pair(k,mapped_type()))).first 迭代器
// (*((this->insert(make_pair(k,mapped_type()))).first)).second 返回value的值的參照 operator[]的原型
Map[e]++;// 有插入、查詢和修改的功能 返回value的值的參照
}
Map["梨子"];// 插入
Map["梨子"] = 5;// 修改
cout << Map["梨子"] << endl;// 查詢 一般不會用 operator[] 來進行查詢,因為沒找到會進行插入
Map["哈密瓜"] = 3;// 插入+修改
for (auto& e : Map)
{
cout << e.first << ":" << e.second << endl;
}
}
執行結果如下:

範例2: 測試map的插入、刪除和迭代器的使用
void test_map1()
{
map<int, int> m;
// 鍵值對
// pair<T1, T2>(T1(), T2()) 通過建構函式構造一個匿名物件
// make_pair(T1() , T2()) 是一個模板函數,返回的是pair的匿名物件,用起來更方便
//m.insert(pair<int, int>(1, 1));
m.insert(make_pair(1, 1));
m.insert(pair<int, int>(2, 2));
m.insert(pair<int, int>(3, 3));
m.insert(pair<int, int>(4, 4));
map<int, int>::iterator it = m.begin();
while (it != m.end())
{
// *it 返回 值得參照
cout << (*it).first << ":" << (*it).second << endl;
// it-> 返回 值的地址 -> 解除參照存取兩個元素
// cout << it->first << ":" << it->second << endl;
++it;
}
// e是自定義型別,傳參照防止有拷貝構造發生
for (auto& e : m)
{
cout << e.first << ":" << e.second << endl;
}
}
執行結果如下:

multiset
概述
- multiset是按照特定順序儲存元素的容器,其中元素是可以重複的
- 底層是紅黑樹,和set特點基本類似,但是multiset可以存放多個key相同的元素
用法
void test_multiset()
{
multiset<int> ms;
// multiset 和 set 的介面基本一致,multiset可以插入重複的
ms.insert(1);
ms.insert(5);
ms.insert(3);
ms.insert(2);
ms.insert(3);
multiset<int>::iterator pos = ms.find(3);// 返回的是第一個3
cout << *pos << endl;
++pos;
cout << *pos << endl;
++pos;
cout << *pos << endl;
++pos;
for (auto e : ms)
{
cout << e << " ";
}
cout << endl;
}
執行結果如下:

multimap
概述
-
multimaps是關聯式容器,它按照特定的順序,儲存由key和value對映成的鍵值對<key, value>,其中多個鍵值對之間的key是可以重複的。
-
底層也是紅黑樹,和map的性質基本類似
用法
void test_multimap()
{
// multimap 和 map 的區別:可以有相同的key
// 不支援operator[] 因為有多個key時,不知道返回哪個key對應的value的參照
multimap<int, int> mm;
mm.insert(make_pair(1, 1));
mm.insert(make_pair(1, 2));
mm.insert(make_pair(1, 3));
mm.insert(make_pair(2, 1));
mm.insert(make_pair(2, 2));
for (auto& e : mm)
{
cout << e.first << ":" << e.second << endl;
}
}
執行結果如下:

紅黑樹封裝map和set
這裡是我關於紅黑樹的部落格——資料結構高階--紅黑樹(圖解+實現) - 一隻少年AAA - 部落格園 (cnblogs.com)
對紅黑樹進行改造
紅黑樹節點框架:這裡和紅黑樹部落格中寫的不一樣,類變成了結構體,紅黑樹部落格那裡沒有介紹鍵值對pair,本文介紹了,所以進行了改進,類和結構體沒有本質的區別
enum Color
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Color _color;
RBTreeNode(const T& data, Color color = RED)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _color(color)
{}
};
紅黑樹框架:
template<class K, class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
private:
Node* _root = nullptr;
};
這裡的紅黑樹是一個KV模型,我們要用這個紅黑樹同時封裝出map和set兩個容器,直接使用這棵紅黑樹顯然是不行的,set屬於是K模型的容器,我們要做怎樣的改造才能夠同時封裝出這兩個容器呢?
這裡我們參考STL原始碼的處理方式,下面是原始碼的部分截圖:
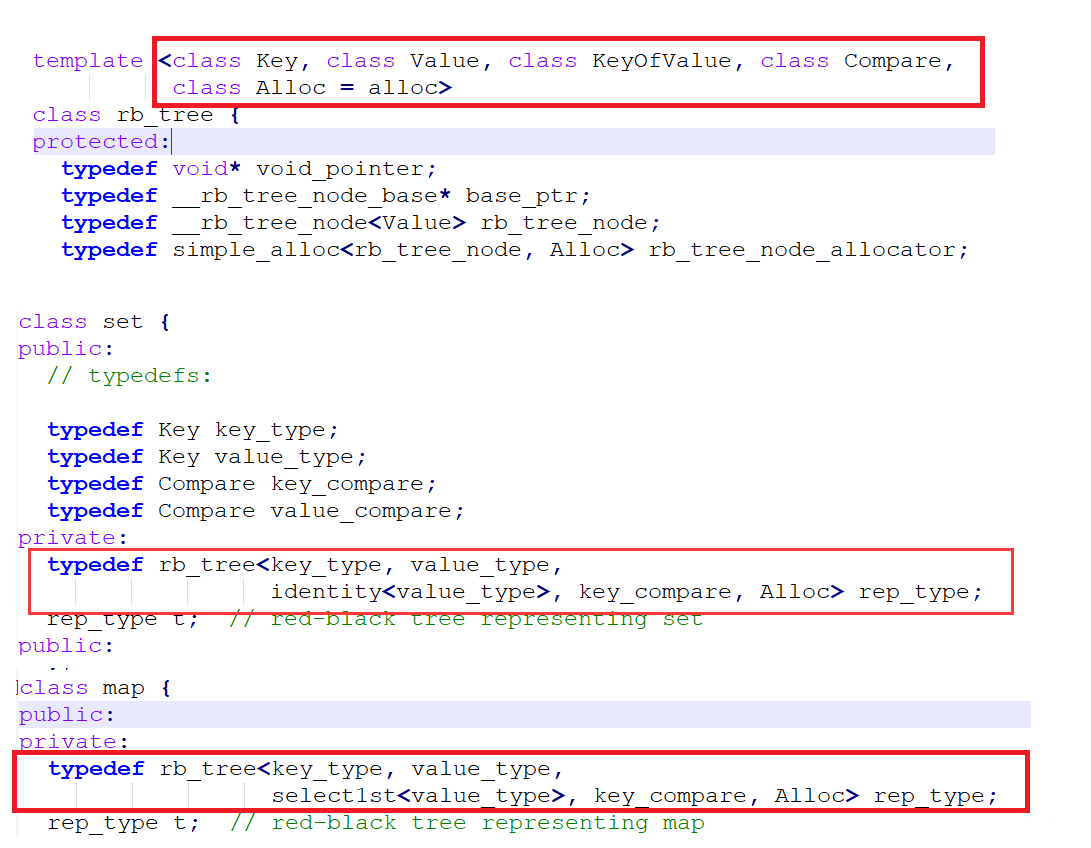
可以看出這裡,紅黑樹的第一個類別範本引數和之前是一樣的,但是第二個引數value和之前是不一樣的,這裡的直接把value存放在節點裡面,通過map和set構造紅黑樹可以看出value存的是pair<K, V>或K,對於map而言,value存的是pair<K, V>;對於set而言,value存的是K。所以這裡的紅黑樹暫時可以這樣改造:
template <class K,class T>
class RB_Tree
{
// 根據T的型別判斷是map還是set 可能是pair<K, V>或K
typedef RBTree_Node<T> Node;
public:
private:
Node* root = nullptr;
};
同時,我們還會發現,上面的紅黑樹的類別範本中有第三個引數是什麼呢?
為了獲取value中的key值,我們可以讓map和set各自傳一個仿函數過來,以便獲得各自的key值
兩個仿函數如下:
template<class K, class V>
class map
{
struct MAPOFV
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
};
template<class K>
class set
{
struct SETOFV
{
const K& operator()(const K& key)
{
return key;
}
};
};
迭代器的實現:
其中operator++就是通過非遞迴中序遍歷的方式走一遍紅黑樹,走到空就結束
template<class T, class Ptr, class Ref>
struct __rbtree_iterator
{
//typedef __rbtree_iterator<T, T*, T&> iterator;
typedef __rbtree_iterator<T, Ptr, Ref> Self;
typedef RBTreeNode<T> Node;
Node* _node;
__rbtree_iterator(Node* node)
:_node(node)
{}
// 返回值(data)的地址
Ptr operator->()
{
return &_node->_data;
}
// 返回值(data)的參照
Ref operator*()
{
return _node->_data;
}
Self& operator++()
{
// 1.先判斷右子樹是否為空,不為空就去右子樹找最左節點
// 2.右子樹為空,去找孩子是其左孩子的祖先
Node* cur = _node;
if (cur->_right)
{
cur = cur->_right;
while (cur->_left)
{
cur = cur->_left;
}
}
else
{
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
cur = parent;
}
_node = cur;
return *this;
}
Self& operator--()
{
// 1.先判斷左子樹是否為空,不為空就去左子樹找最右節點
// 2.右子樹為空,去找孩子是其右孩子的祖先
Node* cur = _node;
if (cur->_left)
{
cur = cur->_left;
while (cur->_right)
{
cur = cur->_right;
}
}
else
{
Node* parent = cur->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
cur = parent;
}
_node = cur;
return *this;
}
bool operator!=(const Self& s)
{
return _node != s._node;
}
};
紅黑樹修改後的程式碼:
#pragma once
#include <iostream>
#include <vector>
#include <time.h>
using namespace std;
enum Color
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Color _color;
RBTreeNode(const T& data, Color color = RED)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _color(color)
{}
};
template<class T, class Ptr, class Ref>
struct __rbtree_iterator
{
typedef __rbtree_iterator<T, Ptr, Ref> Self;
typedef RBTreeNode<T> Node;
Node* _node;
__rbtree_iterator(Node* node)
:_node(node)
{}
// 返回值(data)的地址
Ptr operator->()
{
return &_node->_data;
}
// 返回值(data)的參照
Ref operator*()
{
return _node->_data;
}
Self& operator++()
{
// 1.先判斷右子樹是否為空,不為空就去右子樹找最左節點
// 2.右子樹為空,去找孩子是其左孩子的祖先
Node* cur = _node;
if (cur->_right)
{
cur = cur->_right;
while (cur->_left)
{
cur = cur->_left;
}
}
else
{
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
cur = parent;
}
_node = cur;
return *this;
}
Self& operator--()
{
// 1.先判斷左子樹是否為空,不為空就去左子樹找最右節點
// 2.右子樹為空,去找孩子是其右孩子的祖先
Node* cur = _node;
if (cur->_left)
{
cur = cur->_left;
while (cur->_right)
{
cur = cur->_right;
}
}
else
{
Node* parent = cur->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
cur = parent;
}
_node = cur;
return *this;
}
bool operator!=(const Self& s)
{
return _node != s._node;
}
};
// KOFV是一個仿函數,返回的是對應型別的值 map返回pair中的key set也返回key
template<class K, class T, class KOFV>
class RBTree
{
typedef RBTreeNode<T> Node;// 根據T的型別判斷是map還是set 可能是pair<K, V>或K
public:
typedef __rbtree_iterator<T, T*, T&> iterator;
typedef __rbtree_iterator<T, const T*, const T&> const_iterator;
iterator begin()
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
iterator begin() const
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return const_iterator(cur);
}
iterator end() const
{
return const_iterator(nullptr);
}
pair<iterator, bool> Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data, BLACK);// 根節點預設給黑
return make_pair(iterator(_root), true);
}
Node* cur = _root;
Node* parent = nullptr;
KOFV kofv;
while (cur)
{
parent = cur;
if (kofv(data) < kofv(cur->_data))
cur = cur->_left;
else if (kofv(data) > kofv(cur->_data))
cur = cur->_right;
else
return make_pair(iterator(cur), false);;
}
// 節點預設給紅節點,帶來的影響更小
// 給黑節點的話會影響 每條路徑的黑節點相同這條規則
cur = new Node(data);
Node* newnode = cur;
if (kofv(cur->_data) < kofv(parent->_data))
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}
// 調整顏色
// 情況一:p是紅,g是黑,u存在且為紅
// 調整後的幾種情況:
// 1.如果g為根節點,把g的顏色改成黑,結束;
// 2.如果g不為根節點,
// a.g的父節點為黑,結束;
// b.g的父節點為紅,迭代向上調整,繼續判斷是哪種情況(一和三)
// cur = grandfather;
// father = cur->father;
// 這裡不管cur是在p的左邊還是右邊,都是一樣的,關心的是顏色而不是位置
// 情況二:p是紅,g是黑,u不存在/u為黑 cur p g 三個是一條直線
// 調整方法(左邊為例):1.右單旋 2.把p改成黑,g改成紅
// a. u不存在時,cur必定是新增節點
// b. u存在時,cur必定是更新上來的節點
// 情況三:p是紅,g是黑,u不存在/u為黑 cur p g 三個是一條折線
// 調整方法(左邊為例):1.p左單旋 2.g右單旋 3.把cur改成黑,g改成紅
// a. u不存在時,cur必定是新增節點
// b. u存在時,cur必定是更新上來的節點
while (parent && parent->_color == RED)
{
Node* grandfather = parent->_parent;
// 左邊
if (grandfather->_left == parent)
{
// 紅黑色的條件關鍵看叔叔
Node* uncle = grandfather->_right;
// u存在且為紅
if (uncle && uncle->_color == RED)
{
// 調整 p和u改成黑,g改成紅
parent->_color = uncle->_color = BLACK;
grandfather->_color = RED;
// 迭代 向上調整
cur = grandfather;
parent = cur->_parent;
}
else// u存在為黑/u不存在
{
// 折線用一個左單旋處理 1.p左單旋 2.g右單旋 3.把cur改成黑,g改成紅 cur p g 三個是一條折線
if (cur == parent->_right)
{
RotateL(parent);
swap(parent, cur);
}
// 直線 cur p g 把p改成黑,g改成紅
// 右單旋 有可能是第三種情況
RotateR(grandfather);
parent->_color = BLACK;
grandfather->_color = RED;
}
}
// uncle在左邊
else
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_color == RED)
{
parent->_color = uncle->_color = BLACK;
grandfather->_color = RED;
// 迭代 向上調整
cur = grandfather;
parent = cur->_parent;
}
else
{
// 折線用一個右單旋處理 g p cur g變紅p邊黑
if (cur == parent->_left)
{
RotateR(parent);
swap(parent, cur);
}
// 直線 g p cur 把p改成黑,g改成紅
// 左單旋 有可能是第三種情況
RotateL(grandfather);
parent->_color = BLACK;
grandfather->_color = RED;
}
}
}
_root->_color = BLACK;
return make_pair(iterator(newnode), true);
}
bool Erase(const K& key)
{
// 如果樹為空,刪除失敗
if (_root == nullptr)
return false;
KOFV kofv;
Node* parent = nullptr;
Node* cur = _root;
Node* delNode = nullptr;
Node* delNodeParent = nullptr;
while (cur)
{
// 小於往左邊走
if (key < kofv(cur->_data))
{
parent = cur;
cur = cur->_left;
}
else if (key > kofv(cur->_data))
{
parent = cur;
cur = cur->_right;
}
else
{
// 找到了,開始刪除
// 1.左右子樹都為空 直接刪除 可以歸類為左為空
// 2.左右子樹只有一邊為空 左為空,父親指向我的右,右為空,父親指向我的左
// 3.左右子樹都不為空 取左子樹最大的節點或右子樹最小的節點和要刪除的節點交換,然後再刪除
if (cur->_left == nullptr)
{
// 要刪除節點為根節點時,直接把右子樹的根節點賦值給——root
// 根節點的話會導致parent為nullptr
if (_root == cur)
{
_root = _root->_right;
if (_root)
{
_root->_parent = nullptr;
_root->_color = BLACK;
}
return true;
}
else
{
delNode = cur;
delNodeParent = parent;
}
}
else if (cur->_right == nullptr)
{
if (_root == cur)
{
_root = _root->_left;
if (_root)
{
_root->_parent = nullptr;
_root->_color = BLACK;
}
return true;
}
else
{
delNode = cur;
delNodeParent = parent;
}
}
else
{
// 找右子樹中最小的節點
Node* rightMinParent = cur;
Node* rightMin = cur->_right;// 去右子樹找
while (rightMin->_left)
{
rightMinParent = rightMin;
rightMin = rightMin->_left;
}
//swap(cur->_key, rightMin->_key);
// 替代刪除
cur->_data = rightMin->_data;
delNode = rightMin;
delNodeParent = rightMinParent;
}
break;
}
}
// 沒找到
if (cur == nullptr)
return false;
// 1.替代節點為紅,直接刪除(看上面)
// 2.替代節點為黑(只能有一個孩子或兩個孩子)
// i)替代節點有一個孩子不為空(該孩子一定為紅),把孩子的顏色改成黑
// ii)替代節點的兩個孩子都為空
cur = delNode;
parent = delNodeParent;
if (cur->_color == BLACK)
{
if (cur->_left)// 左孩子不為空
{
cur->_left->_color = BLACK;
}
else if (cur->_right)
{
cur->_right->_color = BLACK;
}
else// 替代節點的兩個孩子都為空
{
while (parent)
{
// cur是parent的左
if (cur == parent->_left)
{
Node* brother = parent->_right;
// p為黑
if (parent->_color == BLACK)
{
Node* bL = brother->_left;
Node* bR = brother->_right;
// SL和SR一定存在且為黑
if (brother->_color == RED)// b為紅,SL和SR都為黑 b的顏色改黑,p的顏色改紅 情況a
{
RotateL(parent);
brother->_color = BLACK;
parent->_color = RED;
// 沒有結束,還要對cur進行檢索
}
else if (bL && bR && bL->_color == BLACK && bR->_color == BLACK)// b為黑,孩子存在
{
// 且孩子也為黑 把brother改成紅色,迭代 GP比GU小1 情況b
brother->_color = RED;
cur = parent;
parent = parent->_parent;
}
// bL存在為紅,bR不存在或bR為黑 情況e 右旋後變色轉為情況d
else if (bL && bL->_color == RED && (!bR || (bR && bR->_color == BLACK)))
{
RotateR(brother);
bL->_color = BLACK;
brother->_color = RED;
}
else if (bR && bR->_color == RED) // 右孩子為紅,進行一個左旋,然後把右孩子的顏色改成黑色 情況d
{
RotateL(parent);
swap(brother->_color, parent->_color);
bR->_color = BLACK;
break;
}
else
{
// cur p b 都是黑,且b無孩子,迭代更新
// parent是紅就結束
brother->_color = RED;
cur = parent;
parent = parent->_parent;
}
}
// p為紅 b一定為黑
else
{
Node* bL = brother->_left;
Node* bR = brother->_right;
if (bL && bR && bL->_color == BLACK && bR->_color == BLACK)// b的孩子全為黑 情況c p變黑,b變紅 結束
{
brother->_color = RED;
parent->_color = BLACK;
break;
}
// bL存在為紅,bR不存在或bR為黑 情況e 右旋後變色轉為情況d
else if (bL && bL->_color == RED && (!bR || (bR && bR->_color == BLACK)))
{
RotateR(brother);
bL->_color = BLACK;
brother->_color = RED;
}
else if (bR && bR->_color == RED) // 右孩子為紅,進行一個左旋,然後把右孩子的顏色改成黑色 情況d
{
RotateL(parent);
//swap(brother->_color, parent->_color);
brother->_color = parent->_color;
parent->_color = BLACK;
bR->_color = BLACK;
break;
}
else// cur 為黑,p為紅,b為黑 調整顏色,結束
{
parent->_color = BLACK;
brother->_color = RED;
break;
}
}
}
else
{
Node* brother = parent->_left;
// p為黑
if (parent->_color == BLACK)
{
Node* bL = brother->_left;
Node* bR = brother->_right;
// SL和SR一定存在且為黑
if (brother->_color == RED)// b為紅,SL和SR都為黑 b的顏色改黑,p的顏色改紅 情況a
{
RotateR(parent);
brother->_color = BLACK;
parent->_color = RED;
// 沒有結束,還要對cur進行檢索
}
else if (bL && bR && bL->_color == BLACK && bR->_color == BLACK)// b為黑,孩子存在
{
// 且孩子也為黑 把brother改成紅色,迭代 GP比GU小1 情況b
brother->_color = RED;
cur = parent;
parent = parent->_parent;
}
// 右孩子存在且為紅,但左孩子不存在或為黑 情況e 右旋後變色轉為情況d
else if (bR && bR->_color == RED && (!bL || (bL && bL->_color == BLACK)))
{
RotateL(brother);
brother->_color = RED;
bR->_color = BLACK;
}
else if (bL && bL->_color == RED) // 左孩子為紅,進行一個右旋,然後把左孩子的顏色改成黑色 情況d
{
RotateR(parent);
swap(brother->_color, parent->_color);
bL->_color = BLACK;
break;
}
else
{
// cur p b 都是黑,且b無孩子,迭代更新
// if (parent == _root) // p是根節點,把b變紅 否則迭代
brother->_color = RED;
cur = parent;
parent = parent->_parent;
}
}
// p為紅 b一定為黑
else
{
Node* bL = brother->_left;
Node* bR = brother->_right;
if (bL && bR && bL->_color == BLACK && bR->_color == BLACK)// b的孩子全為黑 情況c p變黑,b變紅 結束
{
brother->_color = RED;
parent->_color = BLACK;
break;
}
// 右孩子存在且為紅,但左孩子不存在或為黑 情況e 右旋後變色轉為情況d
else if (bR && bR->_color == RED && (!bL || (bL && bL->_color == BLACK)))
{
RotateL(brother);
brother->_color = RED;
bR->_color = BLACK;
}
else if (bL && bL->_color == RED) // 左孩子為紅,進行一個右旋,然後把左孩子的顏色改成黑色 情況d
{
RotateR(parent);
// swap(brother->_color, parent->_color);
brother->_color = parent->_color;
parent->_color = BLACK;
bL->_color = BLACK;
break;
}
else// cur 為黑,p為紅,b為黑 調整顏色,結束
{
parent->_color = BLACK;
brother->_color = RED;
break;
}
}
}
}
}
}
delNodeParent = delNode->_parent;
// 刪除
if (delNode->_left == nullptr)
{
if (delNodeParent->_left == delNode)
delNodeParent->_left = delNode->_right;
else
delNodeParent->_right = delNode->_right;
if (delNode->_right)// 右不為空,就讓右節點的父指標指向delNodeParent
delNode->_right->_parent = delNodeParent;
}
else
{
if (delNodeParent->_left == delNode)
delNodeParent->_left = delNode->_left;
else
delNodeParent->_right = delNode->_left;
if (delNode->_left)// 右不為空,就讓右節點的父指標指向delNodeParent
delNode->_left->_parent = delNodeParent;
}
delete delNode;
delNode = nullptr;
return true;
}
iterator Find(const K& key)
{
if (_root == nullptr)
return iterator(nullptr);
KOFV kofv;
Node* cur = _root;
while (cur)
{
// 小於往左走
if (key < kofv(cur->_data))
{
cur = cur->_left;
}
// 大於往右走
else if (key > kofv(cur->_data))
{
cur = cur->_right;
}
else
{
// 找到了
return iterator(cur);
}
}
return iterator(nullptr);
}
bool IsValidRBTree()
{
// 空樹也是紅黑樹
if (_root == nullptr)
return true;
// 判斷根節點的顏色是否為黑色
if (_root->_color != BLACK)
{
cout << "違反紅黑樹的根節點為黑色的規則" << endl;
return false;
}
// 計算出任意一條路徑的黑色節點個數
size_t blackCount = 0;
Node* cur = _root;
while (cur)
{
if (cur->_color == BLACK)
++blackCount;
cur = cur->_left;
}
// 檢測每條路徑黑節點個數是否相同 第二個引數記錄路徑中黑節點的個數
return _IsValidRBTree(_root, 0, blackCount);
}
int Height()
{
return _Height(_root);
}
private:
// 左單旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
// parent的右指向subR的左
parent->_right = subRL;
if (subRL) subRL->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
subR->_left = parent;
if (ppNode == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
ppNode->_left = subR;
else
ppNode->_right = subR;
subR->_parent = ppNode;
}
}
// 右單旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
// parent的左指向subL的右
parent->_left = subLR;
if (subLR) subLR->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
subL->_right = parent;
if (ppNode == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
ppNode->_left = subL;
else
ppNode->_right = subL;
subL->_parent = ppNode;
}
}
bool _IsValidRBTree(Node* root, size_t k, size_t blackCount)
{
// 走到空就判斷該條路徑的黑節點是否等於blackCount
if (root == nullptr)
{
if (k != blackCount)
{
cout << "違反每條路徑黑節點個數相同的規則" << endl;
return false;
}
return true;
}
if (root->_color == BLACK)
++k;
// 判斷是否出現了連續兩個紅色節點
Node* parent = root->_parent;
if (parent && root->_color == RED && parent->_color == RED)
{
cout << "違反了不能出現連續兩個紅色節點的規則" << endl;
return false;
}
return _IsValidRBTree(root->_left, k, blackCount)
&& _IsValidRBTree(root->_right, k, blackCount);
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return 1 + max(leftHeight, rightHeight);
}
private:
Node* _root = nullptr;
};
總結(改造的幾個點):
- 把類別範本引數的value存放K或pair<K, V>
- 第三個類別範本引數是仿函數,可以獲取第二個類別範本引數中的key
- 增加了迭代器,過載了operator[],具有STL中map中的operator[]一樣的特性
封裝map和set
template<class K, class V>
class map
{
struct MAPOFV
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
typedef RBTree<K, pair<K, V>, MAPOFV> RBTree;
public:
// typename 告訴編譯器這只是一個名字,暫時不用對模板進行範例化
typedef typename RBTree::iterator iterator;
typedef typename RBTree::const_iterator const_iterator;
iterator begin()
{
return _rbt.begin();
}
iterator end()
{
return _rbt.end();
}
const_iterator begin() const
{
return _rbt.begin();
}
const_iterator end() const
{
return _rbt.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _rbt.Insert(kv);
}
bool erase(const K& key)
{
return _rbt.Erase(key);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree _rbt;
};
---------------------------------------------------------------------------
template<class K>
class set
{
struct SETOFV
{
const K& operator()(const K& key)
{
return key;
}
};
typedef RBTree<K, K, SETOFV> RBTree;
public:
// typename 告訴編譯器這只是一個名字,暫時不用堆模板進行範例化
typedef typename RBTree::iterator iterator;
typedef typename RBTree::const_iterator const_iterator;
iterator begin()
{
return _rbt.begin();
}
iterator end()
{
return _rbt.end();
}
const_iterator begin() const
{
return _rbt.begin();
}
const_iterator end() const
{
return _rbt.end();
}
pair<iterator, bool> insert(const K& key)
{
return _rbt.Insert(key);
}
bool erase(const K& key)
{
return _rbt.Erase(key);
}
private:
RBTree _rbt;
};