技術文章 » 【機器學習】李宏毅——Unsupervised Learning

【機器學習】李宏毅——Unsupervised Learning

2022-12-21 12:00:56

讀這篇文章之間歡迎各位先閱讀我之前寫過的線性降維的文章。這篇文章應該也是屬於Unsupervised Learning的內容的。

Neighbor Embedding

Manifold Learning（流形學習）

在實際的資料中，很可能會存在這一種分佈：

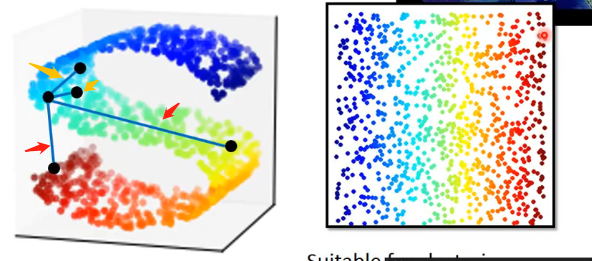
左邊這個分佈可以看成原先在二維平面上的分佈硬塞到一個三維空間之中。

那麼如果我們直接對三維空間的這個分佈計算歐氏距離的話，很可能是行不通的！如果是在比較接近的點（例如圖中我用黃色箭頭標記出來的點）那麼計算歐式距離進行比較還是可以表明它們之間的接近程度的。但是如果在我標註出來的紅色的點，因此它們在三維空間中將原來的二維平面進行了扭曲，因此很可能比較歐氏距離並不能夠象徵它們之間的相似度。這個想法可以用地球在類似，如果在地球上很接近的兩個點那麼計算直線距離當然是可以的；但是如果在很遙遠的兩個點，由於三維空間內的扭曲性，那麼計算直線距離就不行了。

那麼我們如果能夠將該三維空間下的曲面展開成二維空間中分佈（如右圖），那麼我們可以發現它們的分佈就很容易進行劃分，計算歐氏距離也就能夠象徵相似程度了，這也能夠為我們的下游任務提供更多的便利。

下面就來介紹幾種能夠完成非線性降維的方法

Locally Linear Embedding(LLE)

當前我們擁有以下樣本，那麼對於其中的某一個樣本\(x^i\)來說，其各個鄰居為\(x^j\)，那麼它和各個鄰居之間的「關係」為\(w_{ij}\)，如下圖所示：

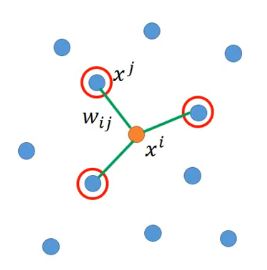
那麼這個關係的確定是認為\(x^i\)可以由各個鄰居\(x^j\)經過線性變換組合而成，即：

\[w^*=argmin_{w} \sum_i \lVert x^i-\sum_jw_{ij}x^j \rVert_2 \]

而假設經過降維之後\(x^i\)對應為\(z^i\)，其需要滿足的條件為降維後各個z之間的關係要保持不變，即：

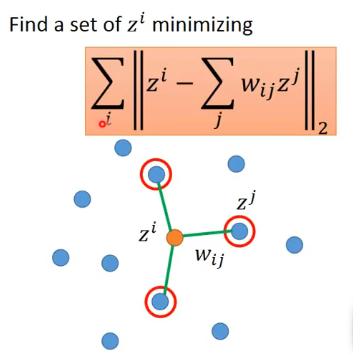
\[Z^*=argmin_Z \sum_i \lVert z^i-\sum_jw_{ij}z^j \rVert_2 \]

那麼採用這一種類似方法的好處在於即使你不知道原來樣本x應該怎麼表示，只要你能夠知道如何計算它們之間的關係，你就仍然可以完成降維。

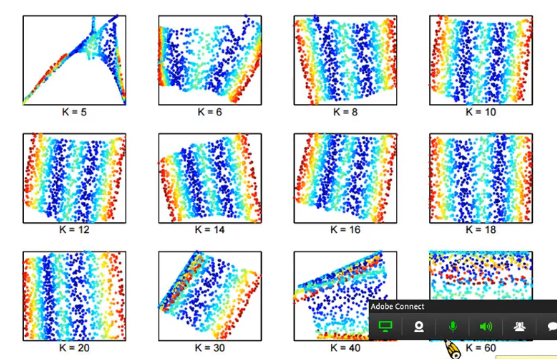
而這個方法需要注意的是要調節選擇的鄰居數目，適合的數目才能夠帶來夠好的效果：

T-distributed Stochastic Neighbor Embedding(t-SNE)

前面提及的各個演演算法雖然都限制了在原來維度中相接近的點，降維之後也要相接近，但是都沒有限制在原來維度中不接近的點，降維之後也要分割開來，因此例如LLE會出現以下情形，即不同類別的點也都擠在了一起：

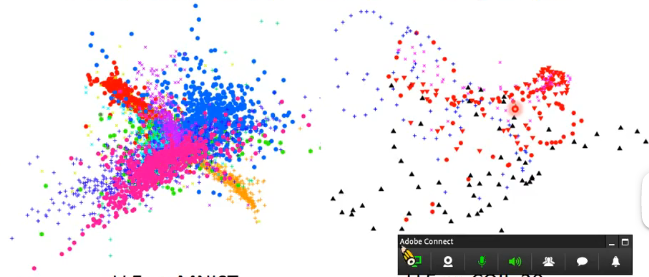
那麼t-SNE的處理方法就較為不同，具體如下：

  • 對於原來的資料x和我們想要降維而成的資料z
  • 在原來的維度空間中對每個樣本計算相似度\(S(x^i,x^j)\)(計算的方法可自行選擇)，再將該相似度轉為分佈，即\(P(x^j \mid x^i)=\frac{S(x^i,x^j)}{\sum_{k\neq i}S(x^i,x^k)}\)
  • 在降維而得到的空間也做相似計算，即\(S'(z^i,z^j)\)和\(Q(z^j\mid z^i)=\frac{S'(z^i,z^j)}{\sum_{k\neq i}S'(z^i,z^k)}\)
  • 而求解方法就是找到一組z，使得分佈P和分佈Q能夠更加接近，相當於最小化這兩個分佈的KL散度，即\(L=\sum_{i}KL(P(*\mid x^i)\mid \mid Q(*\mid z^i))\)

t-SNE在選擇相似度的度量函數的時候有一個很奇妙的地方，其選擇為：

\[S(x^i,x^j)=exp(-\lVert x^i-x^j \rVert_2)\\S'(z^i,z^j)=\frac{1}{1+\lVert z^i-z^j \rVert_2} \]

因為按照我們正常的邏輯應該是在x中選擇什麼樣的度量指標，在z上就選擇一樣的度量指標，但t-SNE這樣選擇的理由，我們需要通過這兩個函數的曲線來說明：

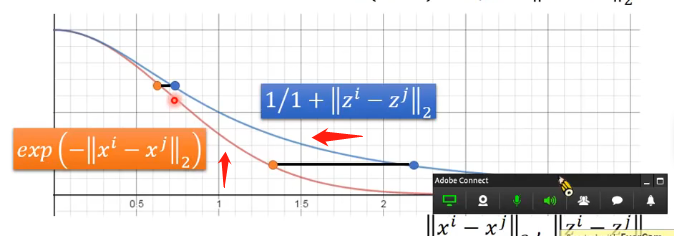
  • 首先，因為我們在進行降維的時候是希望兩個分佈越接近越好，也就是說x降到z之後它們的S是越接近越好，因此在降維的時候應該是在某一點的x直接進行水平方向的平移（保持S不變）找到對應的z
  • 其次，我們可以看到上面兩個橙色的點和兩個藍色的點，從橙色的點降維到藍色的點之後兩個點之間的距離會變大，也就是說如果原來在x中的兩個點很接近，那麼降維之後的點距離被拉開的程度是不嚴重的；但如果在x中兩個點本身就有一定的距離，由於z的函數曲線下降的很慢，因此降維後這個距離就會被拉開很嚴重

因此t-SNE的分類結果大致如下：

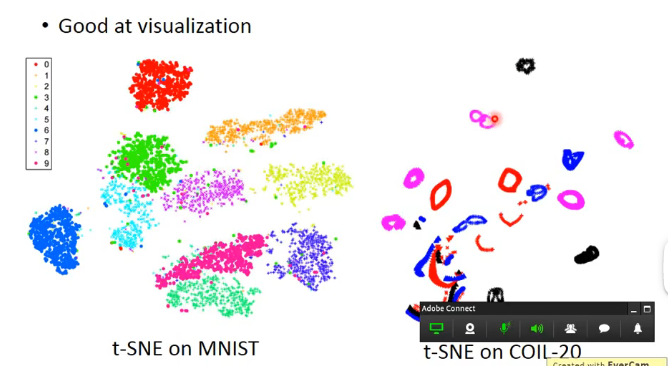
Deep Generative Model

費曼曾經說過：What I cannot create, I do not understand.

那麼這句話用在當前的機器學習之中也同樣適用：因為當前的機器學習雖然可以做到完成分辨的任務，例如分辨出貓和狗，但如果有一天機器可以自己「創造」出一張貓的影象，那麼也許機器才能夠對貓這個名詞的概念有更深的瞭解。而「創造」就是生成模型的任務。因此本節主要是對當前生成模型的研究進行介紹。

PixelRNN

如果對RNN沒有了解且有興趣地可以看我這篇文章，如果不閱讀的話也是可以看得懂接下來PiexlRNN的具體流程的。

假設我們要創造一張\(3\times 3\)的影象，那麼我們可以訓練一個神經網路，它可以不斷接受已經創造出來的畫素點對應的向量，然後輸出下一個畫素點應該對應的向量，如下圖所示：

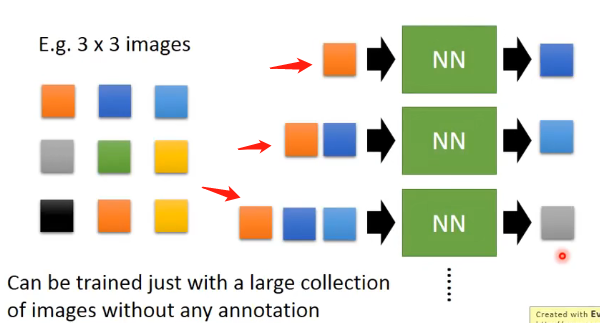
你可能會好奇為什麼每一次輸入的個數都不一樣，其實這是RNN的特性決定的，它可以處理輸入不同個數向量的情況。

那麼李宏毅老師也將這個想法用來創造一些神奇寶貝，但是在訓練的時候發現了以下需要注意的地方，我覺得這些點能夠讓我們在以後的某些工作中受到啟發：

  • 一個畫素點的數值是表示為一個RGB三個通道的，而因為神經網路在輸出的時候通常會經過一個啟用函數（例如Sigmord），而這會導致各個通道的數值一般都很少出現為0或者為1的極端情況，都是聚集在中間。而由於影象的性質如果三個通道的數值都集中在中間那麼就會使得畫素呈現較重的灰色。要產生鮮豔的顏色就必須某些通道接近1，其他通道接近0。對於這個問題的解決方法就是不輸出通道值，將每個畫素點用一個one-hat-vector來表示，其中每一個維度代表一種常見的鮮豔的顏色
  • 但這樣又有一個問題就是顏色太多了會導致這個向量很長，那麼解決方法是將相似的顏色進行聚類，統一成一種顏色來表示，最終表示為160多種顏色。

做出來的效果如下圖：

Variational Auto-encoder(VAE)

What is VAE

VAE是在Auto-encoder進行了改進。首先先介紹在結構和訓練過程上的改進：

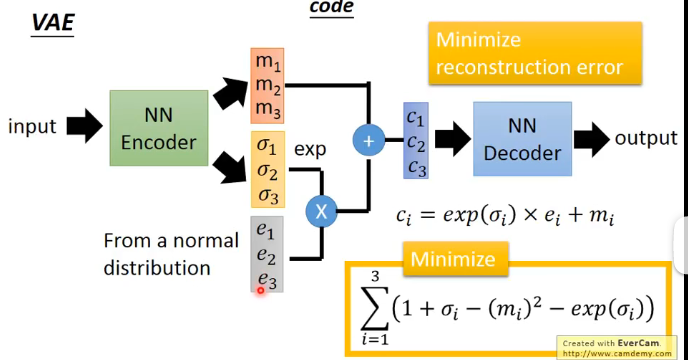
  • 在結構上，VAE的En輸出不只是一個Embedding，而是輸出兩個向量\(M,\sigma\)，然後再從標準正態分佈中產生一個向量\(E\)，接下來的操作就是圖中生成向量\(C\)的操作了，然後再將C放入De之中還原出輸入
  • 在訓練上，VAE不僅僅要求還原出來的輸出要跟輸入儘可能接近，還需要最小化右下角的式子

因此訓練完成之後就可以將VAE的De取出來做生成任務。

Why VAE

為什麼Auto-encoder不夠，而需要改進的VAE呢？我們通過下面這個例子來進行解釋。

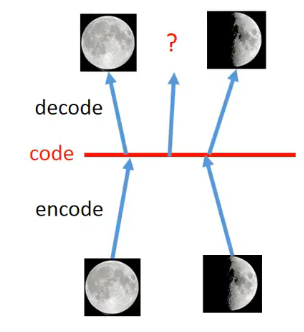
假設Auto-encoder做的事情是下面的，將月亮的圖片變成Code，再還原成月亮的圖片，那麼如果在滿月和半月對應的Code之間選擇一個點，進行還原的話，是否還原出來的圖片也會像是滿月和半月之間的月亮呢？不會！因為Auto-encoder只學習了對應的滿月和半月兩個點的轉換，中間的轉換並沒有學習，因此轉換出來很難想象是什麼東西。

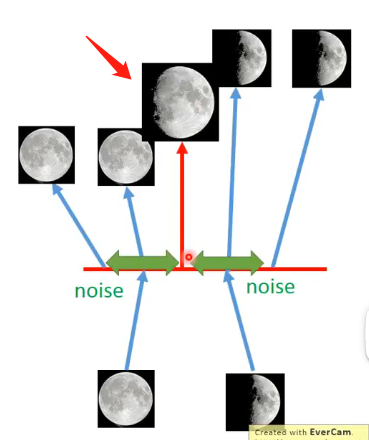
但對於VAE來說，它不僅僅是對滿月和半月這兩個點來進行學習，它還加入了一定的噪聲，同時學習過程之中還要求加入噪聲之後也要還原出原來的圖片，因此在滿月的Code對應的點的附近就都能夠還原出滿月。而如果滿月的噪聲的範圍和半月的噪聲的範圍有交集，在這個交集之中因為VAE既學習了要像滿月，也學習了要像半月，因此真的有可能就會在該點Code上還原出一張介於滿月和半月之間的圖片。

那再讓我們回頭來看VAE是如何改進Auto-encoder就可以理解中間各個向量的含義了：

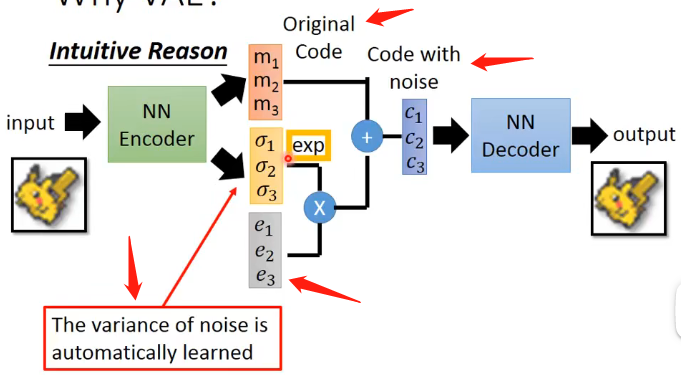
其中向量\(M\)就可以認為是原始的Code，而向量\(E\)可以認為是噪聲，那麼\(exp(\sigma)\)向量就可以認為是控制原始向量和噪聲之間的一個超引數的度量，那麼就得到了向量C。

而對於VAE來說訓練時僅僅要求輸入和輸出類似是不夠的，因為這樣會導致向量\(exp(\sigma)\)取接近於0，從而來導致噪聲幾乎沒有，那這樣就可以做到輸入輸出很接近，因此還需要加上的限制就是下面的式子：

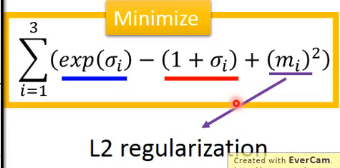
其中前兩項可以簡單理解為限制它不會讓噪聲直接失去掉，第三項則是類似於正則化的思想。

我們也可以從另外一個角度來進行分析，假設我們把Code的取值看成具有一定的分佈：

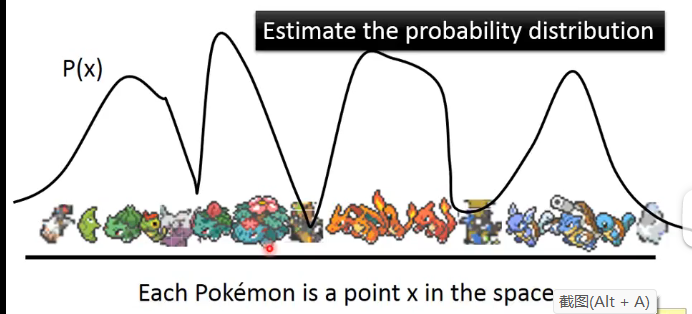
其中在一些能夠還原出比較像寶可夢圖片的Code的取值上就具有較多的概率，而如果還原出來的影象不正常那麼就具有較小的概率，那如果我們能夠估計出來這個分佈就可以通過取樣來產生寶可夢了。因此對於分佈的概率需要介紹下面的混合高斯分佈。

對於一般的混合高斯分佈來說，其中具有的高斯分佈的數量是固定的，即：

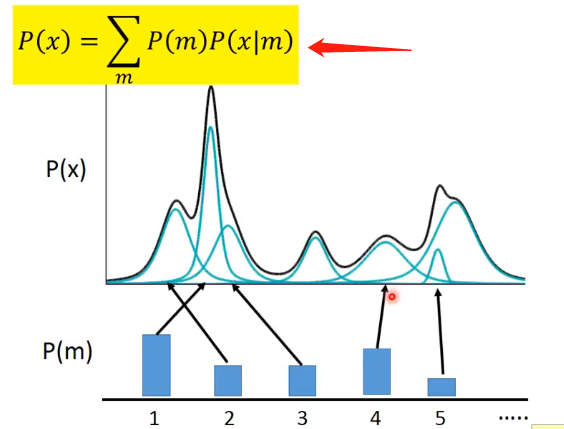
可以看到其表示式是採用求和的形式。那麼從這種高斯分佈中進行取樣的步驟就是先產生一個正整數代表從哪一個高斯分佈進行取樣，之後再在對應的高斯分佈中取樣即可。

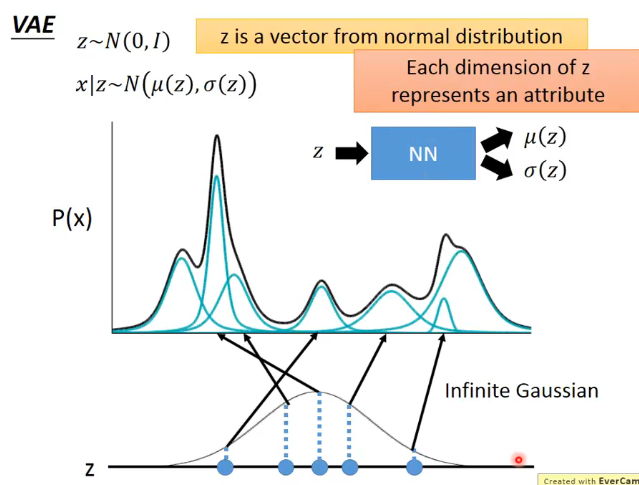
但有另外一種混合高斯分佈其含有的高斯分佈的數量可以認為是無限的，且每一個高斯分佈都有其對應的均值和方差。那麼我們如何來表示這種混合高斯分佈，或者說我們如何從這種高斯分佈中進行取樣呢？

具體做法為：首先先從一個標準正態分佈中取樣得到一個向量z，再將這個向量z通過計算均值的函數和通過計算方差的函數，算出應該對應的高斯分佈的均值和方差，然後再在這個高斯分佈中進行取樣得到x。那麼就有需要注意的點：

  • 首先這個計算均值和方差的韓式應該怎麼確定？這部分是根據實際場景來的，更可以認為是一個神經網路也是行得通的。
  • 總體的混合高斯分佈的表示應該為：\(P(x)=\int_zP(z)P(x\mid z)dz\)

那麼一般情況並不是我們擁有這樣的混合高斯函數讓我們從中進行取樣，而是我們已經有了樣本資料集，我們假設它符合混合高斯的分佈，然後我們需要推匯出這個混合高斯分佈的式子（實際上也就是推匯出那個對z產生對應均值和方差的神經網路）。那麼計算的方法為：

\[\mu(z)^*,\sigma(z)^*=argmax_{(\mu(z),\sigma(x))}\sum_xlogP(x) \]

其實也就是微調那個神經網路的引數，通過梯度下降來實現：

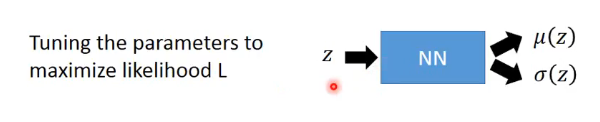
那麼現在就來進行推導：

  • 首先我們需要另外一個分佈\(q(z\mid x)\)，它表示給定樣本x，它將會產生對應的均值和方差，然後z再從這個均值和方差對應的高斯分佈中進行取樣，即：

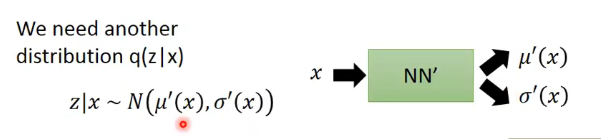
  • 那麼我們對之前的式子進行一定的推導與變換：

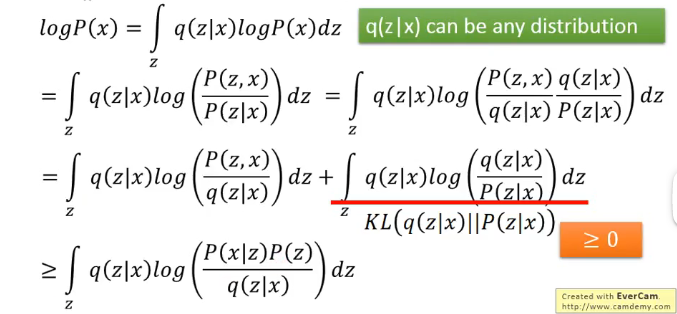
注意這裡的\(q(z\mid x)\)可以是任何分佈是因為後面的積分會將其積分成1，而最下面的這一項我們可以認為是\(logP(x)\)的下界，因此我們現在的目標就更換為：

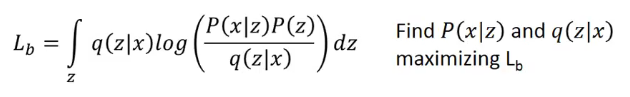
  • 將這個下界的表示式進行整理得到：

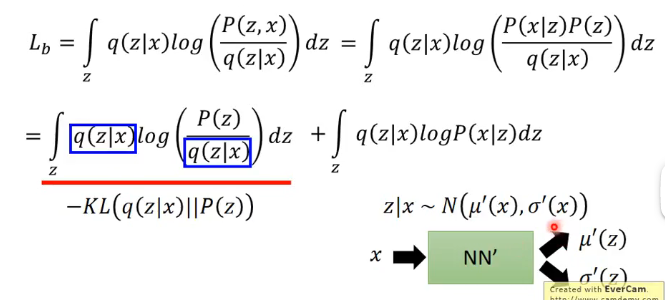
因此我們要最大化上面這兩項

  • 那麼第一項就相當於最小化它們的散度，而最小化散度經過推導也就是最小化下面這個式子：

  • 而最大化第二項我們也可以進行寫成：

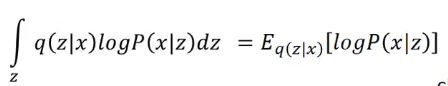
就可以認為是從\(q(z\mid x)\)中取樣得到一個z，然後我們要讓\(logP(x\mid z)\)最大，那麼這也就是Auto-encoder所做的事情：

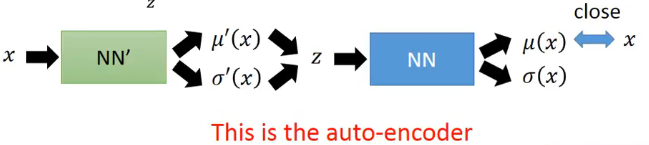
結合我們前面說到的兩個分佈都可以用神經網路來描述就可以理解了。那麼這兩者的結合，就是VAE的loss函數了

Problem of VAE

VAE有一個很嚴重的問題就是它永遠只是在學習怎麼產生一張圖片能夠和原始資料的影象越來越接近，它始終沒有學習如何產生能夠以假亂真的圖片，或者說它只懂得了儘可能地模仿訓練集的影象，例如下面的例子：

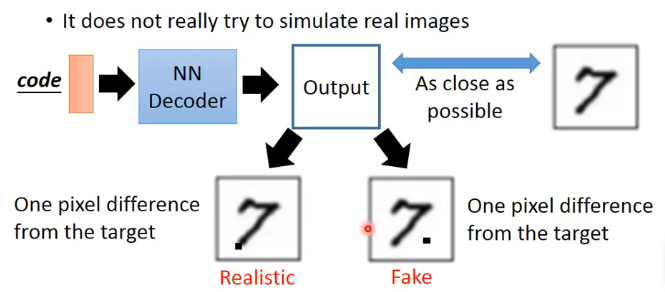
假設我們對輸入和輸出的相似度的計算是使用展開成向量然後計算平方差，那麼上圖的例子中兩個不同的問題雖然都是存在一個畫素點的不同，這在我們計算平方差的時候是一樣的，但時在實際的影象上是很不一樣的。因此如果能夠像GAN一樣學習如何欺騙過辨別器，那就可以產生很好的效果。

GAN

對於GAN的介紹可以看我這篇文章。