技術文章 » 【機器學習】李宏毅——Anomaly Detection（異常檢測）

【機器學習】李宏毅——Anomaly Detection（異常檢測）

2022-12-20 21:01:13

異常檢測概述

首先要明確一下什麼是異常檢測任務。對於異常檢測任務來說，我們希望能夠通過現有的樣本來訓練一個架構，它能夠根據輸入與現有樣本之間是否足夠相似，來告訴我們這個輸入是否是異常的，例如下圖：

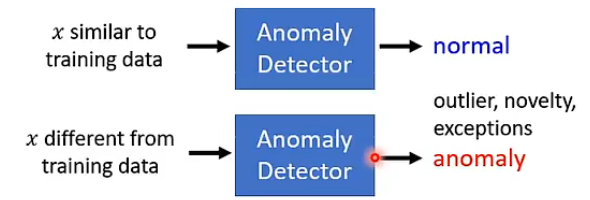
那麼這裡「異常」具體的含義要根據我們訓練集而定，不是說異常就一定是不好的東西，例如下面幾個例子就可以更好的理解：

那麼異常檢測的應用場景非常地多樣，例如檢測消費記錄是否異常、檢測網路連線是否異常、檢測是否異常等等。

那麼這個異常檢測的任務是否感覺很像二分類問題呢？即我們有正類（正常）和負類（異常）的樣本，然後將其放入訓練器中不斷地訓練最後得到想要的模型。
但實際上是很難按照這樣的做法來實現的！因為正類的樣本實際上我們很容易收集到，但是負類的樣本可以說很難收集，或者說負類樣本是無窮無盡的，沒有辦法讓機器學習到每一種負類樣本的特徵，例如下圖的非神奇寶貝的物品是無法窮舉的：

另外一個問題是異常的例子通常很難被收集到，例如網路的異常存取或者異常的交易資料等等，都是在大量的正常資料中才能夠找到一個異常資料，因此這也是很嚴重的問題。

現在我們需要理清楚我們的思路和策略，對於我們當前想要用來做異常檢測所擁有的\(\{x^1,x^2,...,x^N\}\)，可能會有以下幾種情況：

  • 這些樣本是擁有label的，即\(\{\hat{y}^1,...,\hat{y}^N\}\)，那麼我們就可以用來訓練一個分類器；但是我們希望分類器在見到某種樣本和當前已知的資料集中的樣本不接近，可以認為是機器沒有見過的樣本時，它能夠為該樣本貼上標籤為"unknown"，這種稱為Open-set Recognition
  • 這些樣本是沒有label的，這種情況就需要再進行劃分
    • 擁有的這些樣本都是正類樣本，即這些樣本都是「乾淨」的
    • 擁有的這些樣本之中存在部分異常樣本，即這些樣本是受到「汙染」的

下面對各個情況進行介紹

Case 1：存在標籤

我們從辛普森家族的例子來進行講解，假設當前收集了很多該家族的圖片並加上了標籤，即：

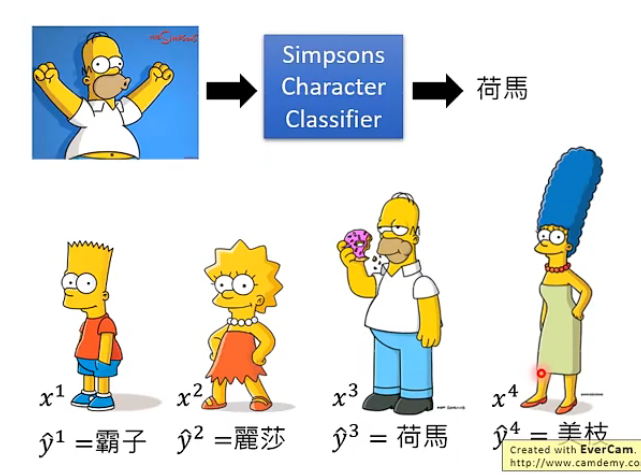
那我們希望就是訓練一個分類器，它能夠讀取一張圖片並作出預測，預測它是這個家族中的誰。

那麼如何將這個任務和異常檢測掛鉤呢，或者說我們如何檢測不是這個家族的人的影象呢？具體的做法是：我們可以讓分類器在輸出類別的時候同時也輸出一個數值，該數值表示它認為這張圖片是這個類別的信心有多大，那麼我們事先也設定一個閾值\(\lambda\)，如果信心大於閾值則說明機器認為是這個家族中的人，則可以認為是正常的；否則說明機器很沒有信心，那麼就很有可能不是該家族中的人，如下圖：

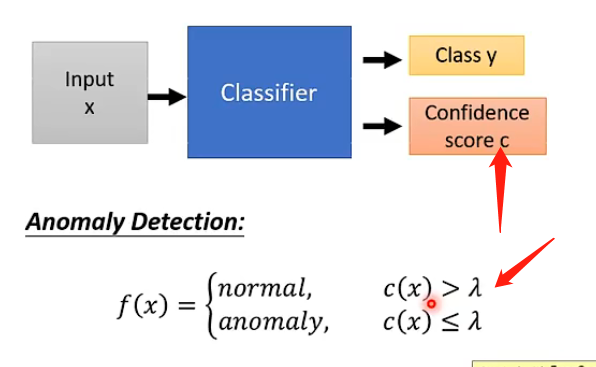
那麼如何來計算這個Confidence score呢？常見的方法就是如果機器的輸出是一個向量，記錄了它認為分類是哪一個類別的各個概率/資訊，那我們可以取該向量中的最大值來作為信心分數，因為如果機器很肯定那麼其最大值肯定很大，否則就會很平均，最大值也會比較小，如下圖；

或者我們也可以將這個向量看成一個概率分佈，然後計算該概率分佈的資訊熵，因為對於概率分佈來說如果它的各個取值的概率越平均則資訊熵越大，否則資訊熵越小，那麼上面的例子中就是第一個的資訊熵很小，第二個的資訊熵很大，那麼我們就要設定小於閾值才是正常的，大於才是不正常的。

但是這樣的方法可能存在一定的問題，就是它可能只學習到正常樣本的某種特別明顯的標籤而已，例如這樣就很可能只學習到辛普森家族的人物的臉都是黃色的，那麼如果將其他異常樣本也塗成黃色的，那麼就很可能可以得到很高的信心分數：

那麼這個問題的根本原因可能是異常樣本實在是太少了，那麼解決的辦法也有，類似於可以用GAN來生成異常樣本，然後需要教機器如果看到異常的樣本就需要給它較低的信心分數，說到底還是通過增加異常樣本來緩解該問題。

Example Framework

我們現在來將系統的流程進行梳理：

  • 訓練的時候我們很多辛普森家族任務的照片和對應的標籤，並訓練一個分類器，它能夠告訴我們訓練集中的圖片是哪一個辛普森家族的人物並給予一個信心分數
  • 而我們另外訓練一個 Development Set，這個集裡面有很多圖片，包含著是辛普森家族的圖片和不是辛普森家族的圖片，且帶有對應的標籤，這個集合的作用就是用來檢測分類器的好壞，同時將閾值調整到能夠在該集合上表現最好
  • 用測試集來進行檢測和計算泛化效能

而如何衡量分類器的好壞通常不是用正確率這個指標的，因為在異常檢測的大部分場景之中正常樣本和異常樣本的分佈過於懸殊，很可能是好幾百比一的比例，那這樣的話如果機器不管看到什麼樣本都直接說是正常的，也能夠得到很高的正確率。這並不是我們想要的機器！

一般來說異常檢測系統的分類結果可能會有以下幾個可能：

那麼錯誤的情況就是兩種：將正常的檢測為異常的和將異常的檢測為正常的。

那麼如何評價這種分類結果的好壞其實就取決你覺得哪一個分類錯誤更加嚴重，哪一種更嚴重就設定更高的懲罰。

Case 2：不存在標籤

對於不存在標籤的情況，也就是我們只有\(\{x^1,x^2,...,x^N\}\)，而沒有\(\{\hat{y}^1,...,\hat{y}^N\}\)，也就是說我們無法訓練一個分類器來幫助我們進行異常檢測。

那我們的具體想法就是根據樣本資料產生一個分佈\(P(x)\)，正常的樣本在該分佈中得到的概率就高，異常的樣本概率就低，那就可以類似地設定一個閾值將正常和異常的樣本區分開。例如下圖：

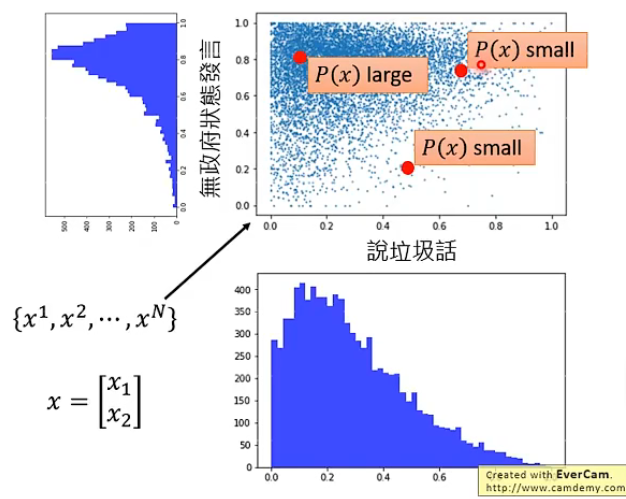
那麼接下來的問題就是如何尋找這個分佈呢？我們可以假設存在一個概率密度函數\(f_{\theta}(x)\)，那麼代入某一個樣本後得到的值就是該樣本被取樣得到的概率。那麼根據極大似然的思想，可以知道應該要找到對應的\(f_{\theta}(x)\)可以使得\(\{x^1,x^2,...,x^N\}\)這些樣本一起出現的概率最大，即

\[L(\theta)=f_{\theta}(x^1)f_{\theta}(x^2)...f_{\theta}(x^N)\\\theta^*=argmax_{\theta}L(\theta) \]

如果不明確極大似然估計的思想，那麼可以這樣簡單理解：我們擁有的這些樣本可以認為是從某個分佈之中不斷取樣得到的，那麼擁有\(\{x^1,x^2,...,x^N\}\)可以認為是一個事件，既然這個事件已經發生了，那麼我們應該覺得這個事件在所有事件中的發生概率應該是最大的，那麼它才會發生，而這個「所有事件」實際上就是由\(\theta\)不同才引起的\(f_{\theta}(x)\)不同，而產生的不同事件。

而常見的，是將該概率分佈設為高斯分佈：

\[f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{\vert \Sigma \vert ^{\frac{1}{2}}}exp\{-\frac{1}{2} (x-\mu)^T\Sigma^{-1} (x-\mu) \}\\\mu^*,\Sigma^*=argmax_{\mu,\Sigma}L(\mu,\Sigma) \]

直觀上看不同的引數所帶來的影響：

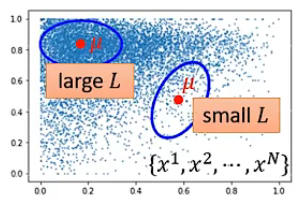
上述式子可以解出來：

\[\mu^*=\frac{1}{N}\sum_{n=1}^Nx^n\\\Sigma^*=\frac{1}{N}\sum_{n=1}^N(x-\mu^*)(x-\mu^*)^T \]

因此我們的異常檢測系統也就明確的，即：

而由於高斯分佈可以有很多維度，因此可以選取很多的特徵來加入這個模型，可能可以使得結果更為精確。並且在實際場景中可以將f(x)加上一個log，因為概率的限制，加上log之後的取值範圍會更大，我們可以找到更好的區分點。