技術文章 » 【機器學習】李宏毅——Recurrent Neural Network(迴圈神經網路)

【機器學習】李宏毅——Recurrent Neural Network(迴圈神經網路)

2022-12-17 12:00:18

假設我們當前要做一個人工智慧客服系統，那該系統就需要對使用者輸入的話語進行辨認，例如使用者輸入：

I want to arrive Taipei on November 2nd

那麼該系統就能夠辨認出來Taipei是目的地，而後面是時間。那麼我們可以用一個簡單的前向網路來實現這個事情，輸出為這個單詞屬於哪個含義的概率。但這會存在問題，例如輸入以下：

I want to leave Taipei on November 2nd

同樣輸入都是Taipei，但是第一個句子是作為目的地，第二個句子是作為出發地，那麼普通的前向網路是無法對同一個輸出做出不同的輸出的。因此就希望此時使用的網路能夠具有一定的記憶性，即在看到Taipei之前因為已經讀入了前一個詞彙(arrive、leave)，那麼就根據這前面的詞彙來進行輔助判斷。

RNN的結構特點

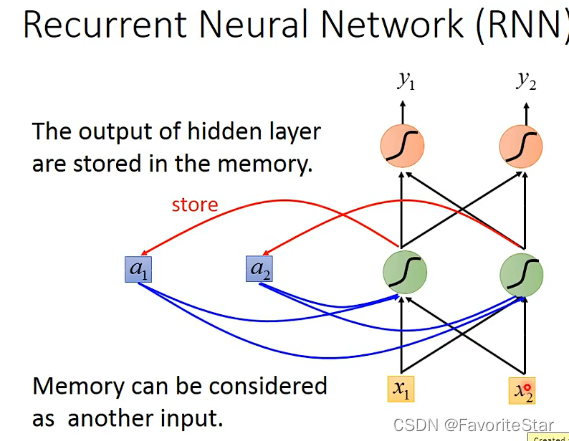
其主要的特點在於每個隱含層的輸出都會存放在一個另外的位置中(\(a_1,a_2\))，並且隱含層接受的輸入包括原本的輸入和當前儲存記憶中的值，假設權重都是1，那麼該隱含層的輸入就是\(a_1+a_2+x_1+x_2\)。並且在第一次輸入的時候由於記憶中沒有值因此需要賦予初始值。

而這樣存在記憶的結構就使得RNN對於輸入的順序是敏感的，不同的輸入之間並不是獨立的，它們順序一旦變化就會引起輸出的大不相同。那麼如果用RNN來處理之前的任務：

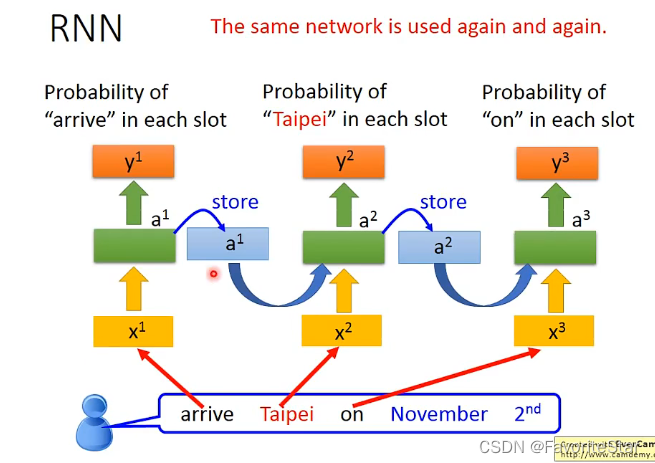
注意這裡並不是用到了三個網路結構，而是同一個網路在不同的時間點被使用了三次。那麼這就可能使得輸入同樣的詞彙結果輸出是不一樣的，因為前面的輸入也會影響該結果。

而RNN同樣也可以往deep發展：

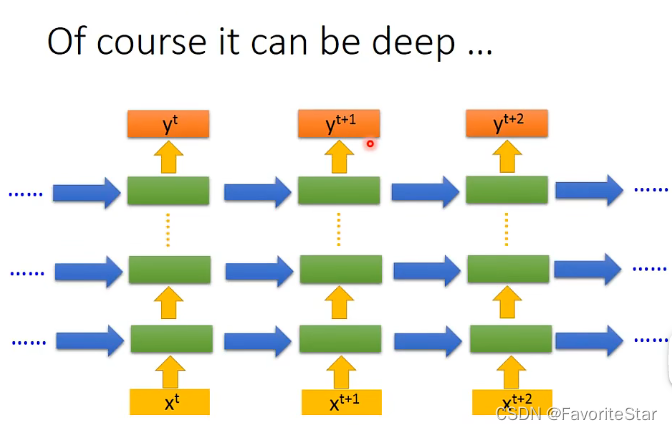
RNN網路的變體

下面介紹RNN網路的變體：

Elman Network & Jordan Network

這兩種網路都是RNN的推廣，架構的主要區別在於：

  • Elman Network每個隱含層的記憶中儲存的是該隱含層的輸出，跟RNN是一樣的
  • Jordan Network中隱含層儲存的都是前一個輸入樣本的輸出\(y^{t-1}\)，這種網路架構具有更好的解釋性因為輸出我們知道它具有什麼含義，而如果是隱含層的輸出我們很難明確其含義，也就很難明確網路學習到什麼東西

Bidirectional RNN（雙向）

這個結構的特點在於對於網路的架構是雙向的，即正向是跟前面一樣，反向呢是從尾部不斷讀到頭部（因為順序不同輸出也就不相同），然後再把每個對應的輸出結合起來給輸出層作為輸入，即將正向的\(x^t\)的輸出和反向的\(x^t\)的輸出一起作為輸出層的輸入得到真正輸出\(y^t\)：

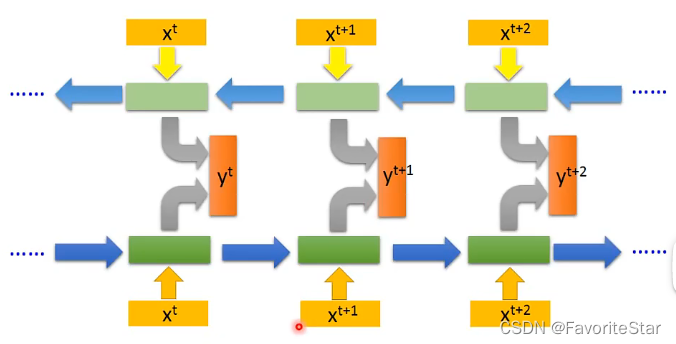
那麼這就導致在在對每個輸入做判斷的時候，相當於綜合了前後的所有資訊來做判斷。

Long Short-term Memory(LSTM)

顧名思義，就是具有比較長期記憶能力的RNN網路，前面的RNN 網路都是隻要有了新的輸入進來，記憶結點中就會被重寫，但LSTM不一樣，其主要特點的結構如下，其具有三個Gate

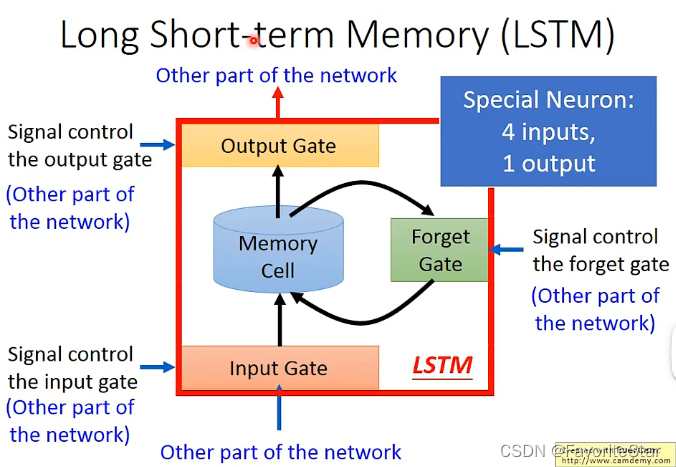
  • Input Gata：輸入端的閘門，在每次有新的輸入進行神經網路後隱含層將會產生新的輸出，而這個新的輸出是否能夠寫入記憶結點中就取決於Input Gata，只有其是開啟狀態才能進行寫入
  • Ouput Gata：輸出端的閘門，只有當該閘門開啟時，才能夠讀取其中的內容來作為隱含層的另一個輸入
  • Forget Gata：該閘門控制什麼時間點應該將當前記憶結點中的內容忘記掉

上面各個Gata的開啟和關閉都是網路自己學習到的。因此每一個記憶結點就有四個輸入（輸入數值和三個控制訊號）和一個輸出

下面來看其具體的運作行為：

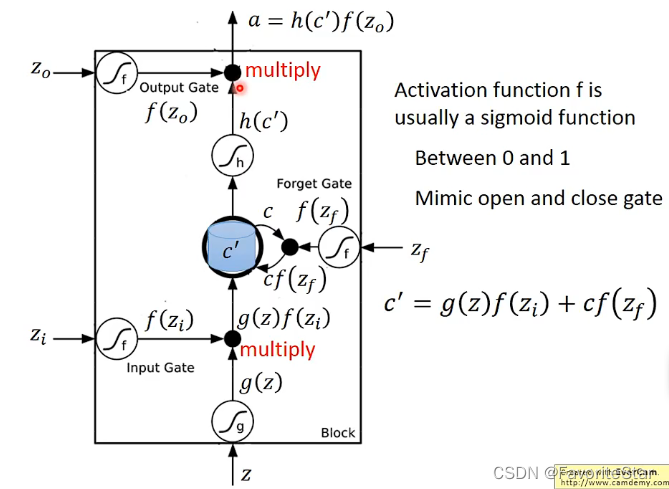
  • 輸出z經過啟用函數g得到g(z)，然後Input Gata的輸出\(z_i\)經過啟用函數(Gata的啟用函數一般為sigmoid)得到\(f(z_i)\)
  • 原來記憶單元中的值為c，而Forget Gate的輸出與c相乘，計算得到\(c`=g(z)f(z_i)+cf(z_f)\)，作為記憶單元中信的儲存值
  • 記憶單元中的值經過h得到\(h(c`)\)，再與輸出單元的輸出相乘並進行輸出

為什麼採用Sigmoid函數來作為Gate的啟用函數呢？因為它的輸出在0到1之間，可以認為是該閘門開啟的程度。而這裡可以看出ForgetGate開啟的時候（輸出為1）是對原來的值進行記憶的，只有關閉的時候才是對原來的值清零的。也可以看出輸出的值跟所有閘門的開啟關閉是息息相關的。這邊所有Gate的輸入都是學習得到的。

上面所說的只是單個結點，整體的網路就相當於將神經元換成這整個記憶單元，如下圖：

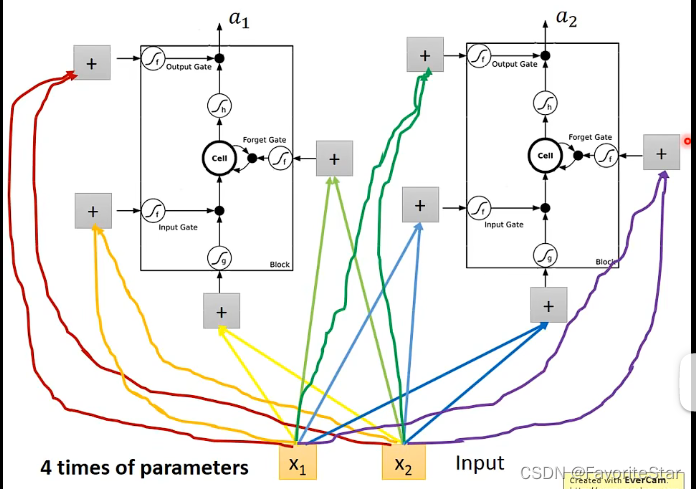
因此認為神經元數目相同時，LSTM引數量是普通的四倍。而實際上LSTM並不會這麼簡單：

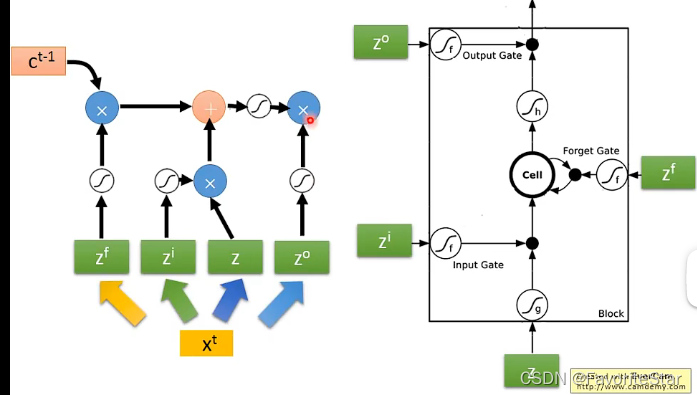
可以認為x是乘以了四個矩陣（權重矩陣）得到了四個向量，這四個向量的長度和該層LSTM記憶單元的數目一樣，然後每一個作為LSTM的輸入，因此剛好就四個輸入，如上圖。因此如果多個串起來就是：

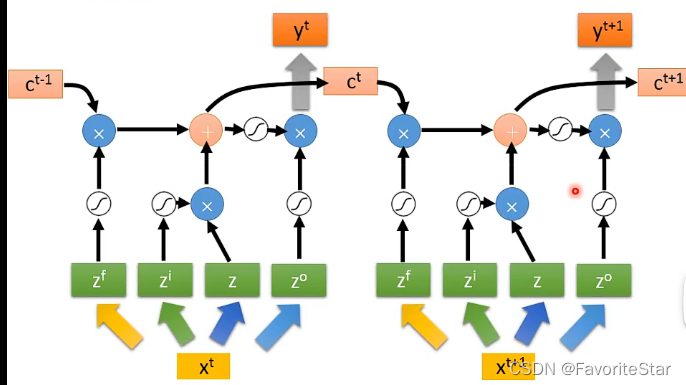
但實際上仍不是LSTM的完全體，完全體如下：

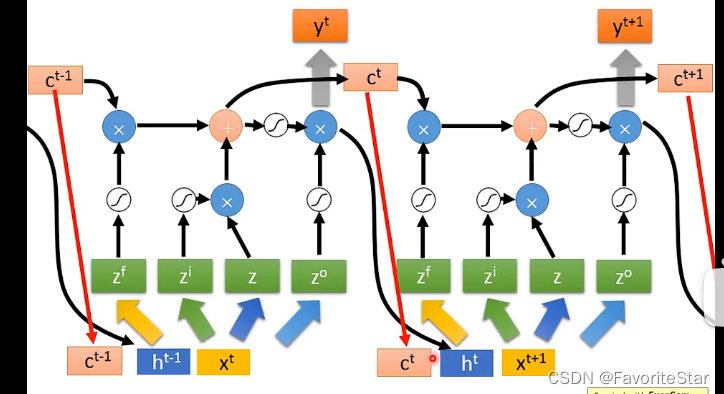
就是將上一層的輸出和記憶單元當前的值和這一層的輸入拼在一起作為輸入，再加上多層：

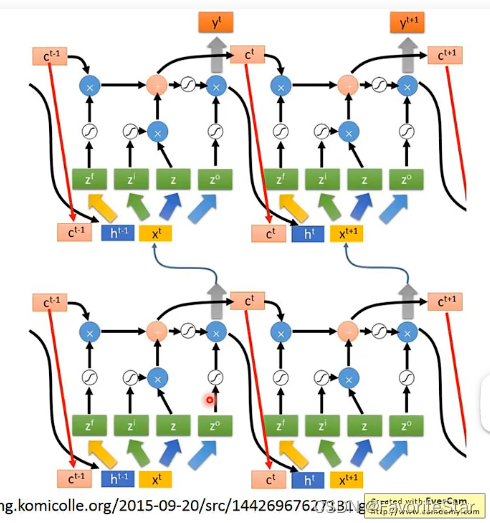
這就是LSTM的完全體了。

Loss Function

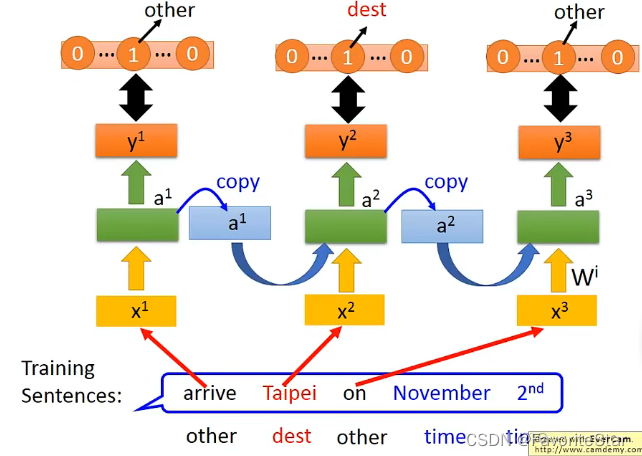
將輸出的詞性或者是標註作為目標向量，損失函數就是輸出向量與目標向量的距離。

學習演演算法Backpropagation through time(BPTT)

跟之前的網路一樣，RNN對於網路引數的學習仍然是採用梯度下降的方式。而為了高效的計算梯度就有了BPTT這個演演算法（課程沒有介紹這部分）。

但是RNN的訓練並不容易：

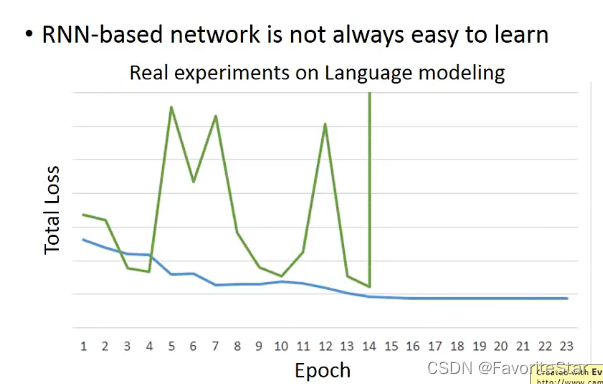
這是因為它的損失函數非常地特殊：

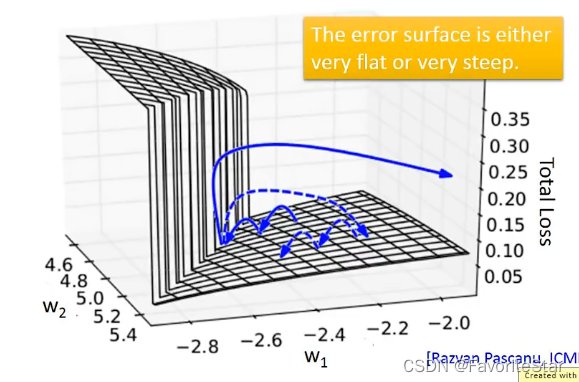
這就導致損失函數計算梯度的時候經常跳動，總體損失也劇烈變化。而實際上做法可以將梯度設定一個閾值，超過則預設為閾值就可以了，不然可能會陡峭導致梯度無窮大。為什麼會有上面這麼陡峭的損失函數呢？來看下圖的結構：

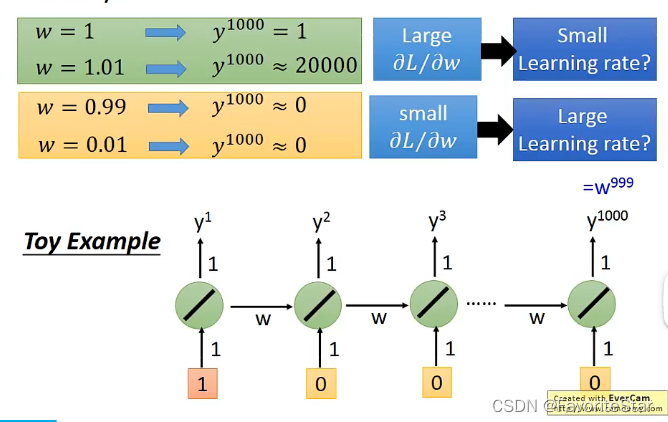
在很小的區間內，權重非常微小的變化就會導致輸出劇烈的變化，因此很難通過學習率來應對。這主要是因為同一個引數在不同的時間點多次被使用所導致的。

而如果將RNN換成LSTM，它可以解決上述出現的梯度消失（Gradient vanishing）的問題，這可能會在面試中提及。

為什麼LSTM可以解決梯度消失的問題

  • RNN裡面每一輪都會使得記憶結點中的值被清洗掉，而在LSTM中可以認為其記憶結點中的值是與輸入進行累加的。因此可以認為一旦權重變化會導致記憶結點中的值發生變化，這個變化就會一直存在（除非Forget Gate決定將其洗掉，這是很少數的情況），因此除非ForgetGate關閉，否則都不會有Gradient vanishing 的問題。RNN中由於每次都清洗，因為可以認為權重的變化而引起的最終結果的變化時劇烈的，而LSTM是在原來有的基礎上做變化，這就可以中和掉一些。

或者可以採用GRU，其只有兩個gate，更簡單但是表現也不差