【機器學習】李宏毅——線性降維

降維，可以用下面這張圖來很簡單的描述，就是將不同的、複雜的多種樹都抽象成最簡單的樹的描述，也就是我們不關心這棵樹長什麼樣子有什麼特別的特徵，我們只需要降維，知道它是一棵樹即可。

維度下降實際上就是找到一個function，使得輸入x得到輸出z，而輸出z的維度要比輸入x的維度小。具體有幾種方面，下面就先將PCA（主成分分析）

PCA

PCA認為，function實際上可以看成一個矩陣，即：

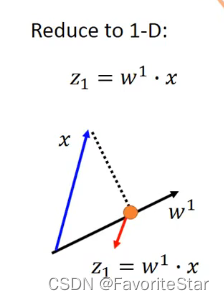
可以通過一個向量與矩陣的運算來描述這件事。那麼當前假設x為二維向量，而要求降到一維的向量z，而w的範數等於1，則可以看成z就是x在w上的投影

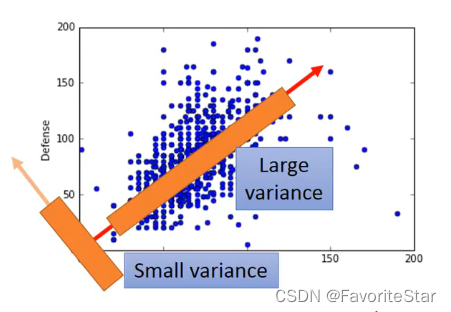
不同方向的w會導致投影出來的z不一樣，因此我們的目標是找到一個w，它能夠使得投影之後的z的差異效能夠最大，而不是都擠在一起，如下圖：

那麼如果是降到多維的話也是同理，首先先找某一維度能夠讓對應方差最大，再找另一維度能夠讓對應方差最大且\(w^2\)與\(w^1\)是正交的，以此類推：

最終得到的\(W\)是正交矩陣。

而經過一系列的推導（此部分推導可以具體看影片，之後我也會把統計學習方法中的推導過程補上）得到的結論就是：假設x的協方差矩陣為\(S=Cov(x)\)，而\(w^i\)就是矩陣S所有特徵值中第i大的特徵值對應的特徵向量。

從另一種角度來看PCA

假設當前有許多個基礎的組成成分，而我們每張圖片都可以看成是由多個組成成分和一個基礎的均值（全數樣本的均值）相加而成的，看成在圖片均值的基礎上擁有自身差異性的部分，那麼根據該圖片中是否有對應的基礎成分就可以寫出來一個向量\(C=[c_1,c_2,...]\)，如果組成成分不是特別多而圖片特別多，那我們用向量C來表示一張圖片是非常有意義的。

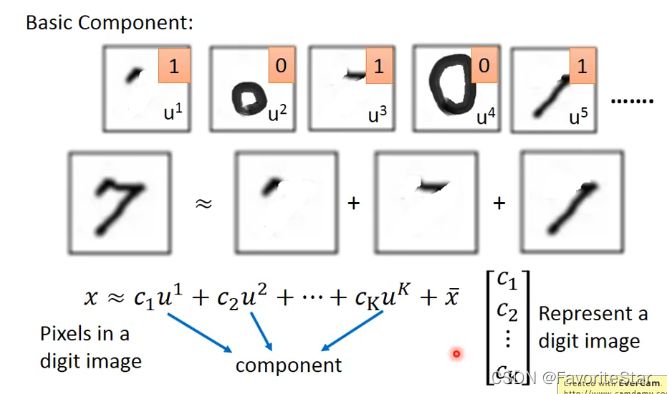
那麼就可以寫成

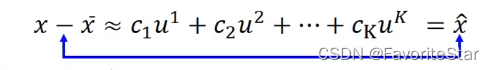
因此我們的思路就轉換成找到一組向量\(\{u^1,u^2,...,u^k\}\)能夠使得 \(x-\bar{x}\)與\(\hat{x}\)之間的距離最小化，即

而可以證明，由PCA方法找出來的向量組\(\{w^1,w^2,...,w^k\}\)就是我們要找的目標向量組。而將上述運算轉換成矩陣形式：

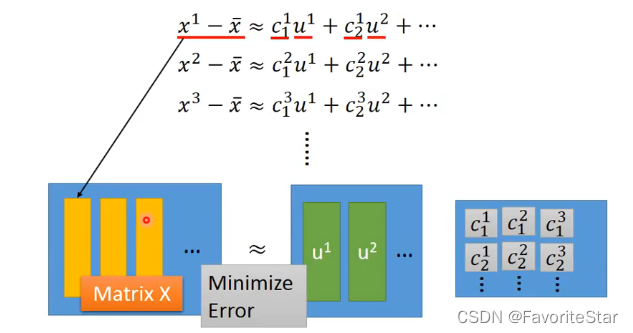
目標就是找出矩陣u和矩陣c，使得他們相乘之後和矩陣X的差距最小。而回顧學過的SVD，矩陣X可以進行分解：

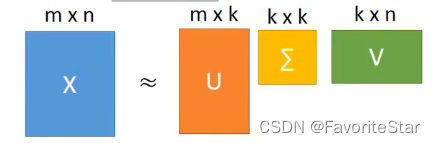
其中矩陣U的k個列向量就是矩陣\(XX^T\)的最大的前k個特徵向量，而\(XX^T\)就是\(S=Cov(x)\)，因此這也就是我們想要找到\(\{w^1,w^2,...w^k\}\)，因此只要進行SVD分解就可以找到目標的\(\{u^1,u^2,...u^k\}\)。那麼下一個問題就是求解矩陣C。

由於我們已知了矩陣U，那麼對於某個樣本，就有：

而由於矩陣W中每一個向量都是相互正交的，就可以有：

(此部分我也不太理解怎麼推匯出來的，希望會的大神教教)。接下來就可以將這一個過程用神經網路的形式來表示：（注意圖中應該是c應該是下標不是上標）。

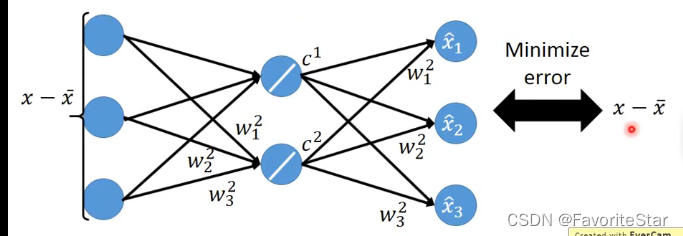
但是如果現在我們不是從SVD中解出矩陣W，而是從這神經網路之中來進行梯度下降求解，這樣求出來的結果和用SVD求出來的結果是不一樣的！因為在SVD中求出來的結果還有限制它們彼此之間是正交的，而神經網路是沒有的。而將PCA看成是具有一個隱含層的神經網路的方式稱為Autoencoder。

但其實用SVD的方式求解起來更快更好，而要學習這種神經網路的方式是因為其隱含層可以加層來實現更復雜的操作。

PCA的缺點

首先是無監督性質，如果樣本本身就具有一定的類別資訊，那麼就會出現下面這樣的問題：

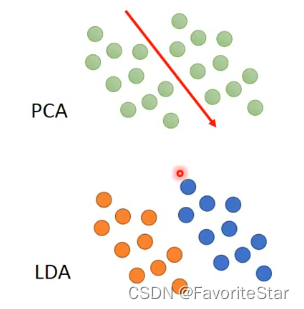
可以看到如果有類別區分那麼做PCA就會將它們混淆在一起。

其次它是線性變換，無法做非線性的事情：

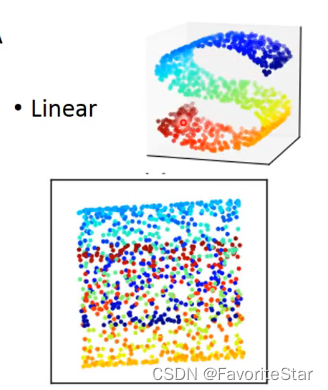
PCA的應用

如果將PCA對人臉資料進行處理：

可以看到各個出來的特徵向量並不是我們想象中的基本組成部分（比如嘴巴什麼的），更像是一張完整的臉，這是為什麼呢？

因為這些向量的組成成分的加權數位並不一定是正的，如果是負數就相當於先畫出一個很複雜的東西然後再減去某個元素。這樣就很不直觀。如果想要加權的引數都是正的，可以採用NMF，它能夠使得引數\(a_i\)都是正的，其次是每個\(w^i\)裡面每個維度的數值都是正的，這是PCA無法保證的，因為在影象中\(w^i\)就象徵第i個組成部分的影象，如果某個畫素是負的那將無法處理，PCA就會出現這個問題。

能夠更明顯地看出組成部分，符合我們的預期。