【機器學習】李宏毅——自注意力機制(Self-attention)

前面我們所講的模型，輸入都是一個向量，但有沒有可能在某些場景中輸入是多個向量，即一個向量集合，並且這些向量的數目並不是固定的呢？

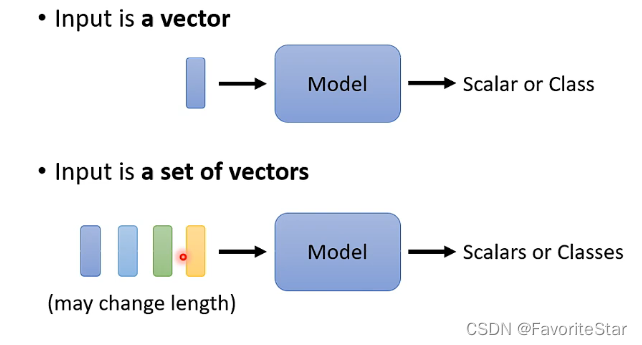
這一類的場景包括文字識別、語音識別、圖網路等等。

那麼先來考慮輸出的型別，如果對於輸入是多個數目不定的向量，可以有以下這幾種輸出方式：

• 每個向量對應一個輸出：輸出的數目與輸入向量的數目一致，例如下圖的詞性識別、語調識別、狀態識別等等：

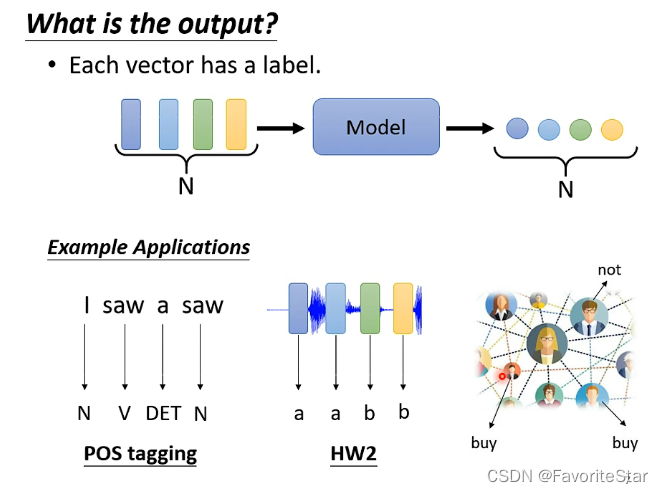
• 只有單個輸出：這種應用於例如判斷一段話的正負面作用、語音辨認說話者等等，如下圖：

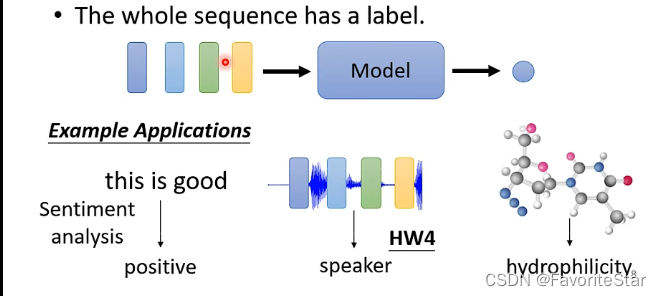
• 機器自己決定輸出多少個結果（seq2seq）：如翻譯、語音轉文字等等。

Sequence Labeling(輸入輸出數目一致)

最簡單的思路當然是將每一個向量單獨作為一個輸入，然後將其丟入到一個全連線之中，每個單獨產生結果。但是這種方法的問題在於沒辦法考慮前後向量之間的聯絡。那麼轉換另一個思路就是開一個window，每次將window中的向量一起輸入到全連線網路中，如下圖：

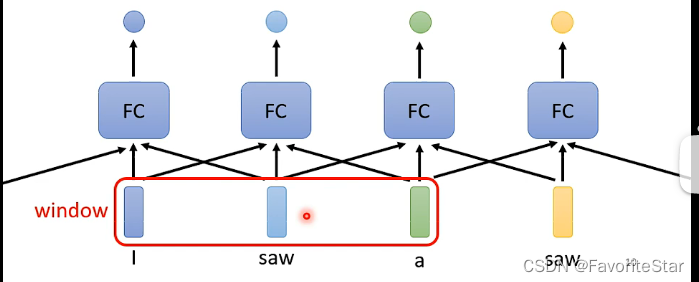
這種方式的問題在於如果遇到某些場景需要全部向量都考慮，但是我們無法事先知道這個場景中向量的數目，我們也就很難調整我們的window去適應。在這種情況下就需要用到自注意力機制了。

Self-attention

可以將自注意力機制看成一層，其接受所有向量的輸入，然後輸出的數目跟輸入的數目的是一樣的，可以認為它的每個輸出都是考慮了整個向量集之後的結果，之後再將這些輸出每個單獨放入一個全連線網路中來得到輸出，這樣可以顯著的降低全連線網路的引數量。並且這個也可以多次使用，自注意力後FC再自注意力再FC等等。

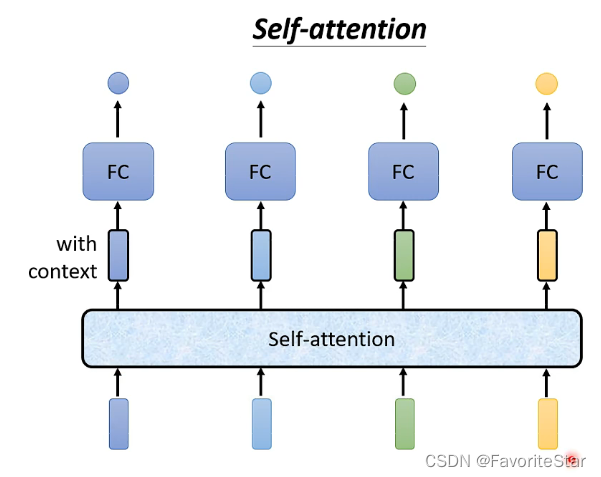
那麼接下來的問題就是這個機制如何接受輸入並作出相應的輸出。這邊以第一個向量對應的第一個輸出為例：

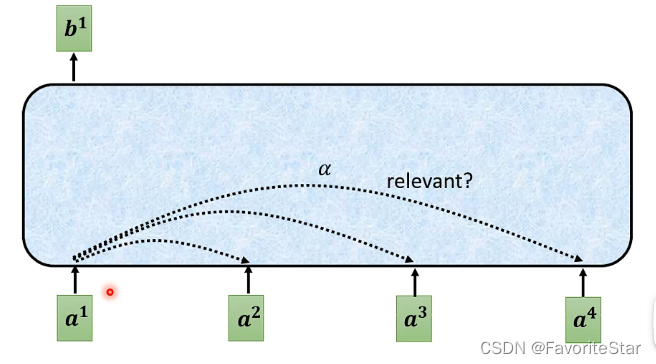
1. 計算每個輸入向量之間的關聯性：計算關聯性\(\alpha\)有很多種方法：

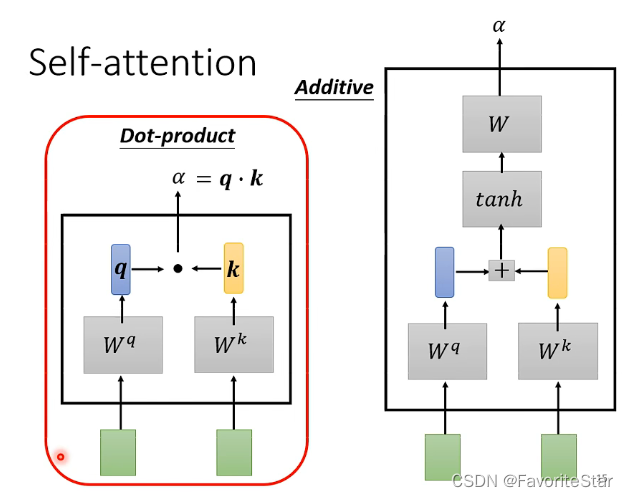
最常見的是這種Dot-product，就是將兩個向量分別乘以一個矩陣，得到新的向量，然後再進行點乘得到一個數值，也就是\(\alpha\)

2. 計算出兩兩向量之間的相關性後進行Sortmax：如下圖：
   

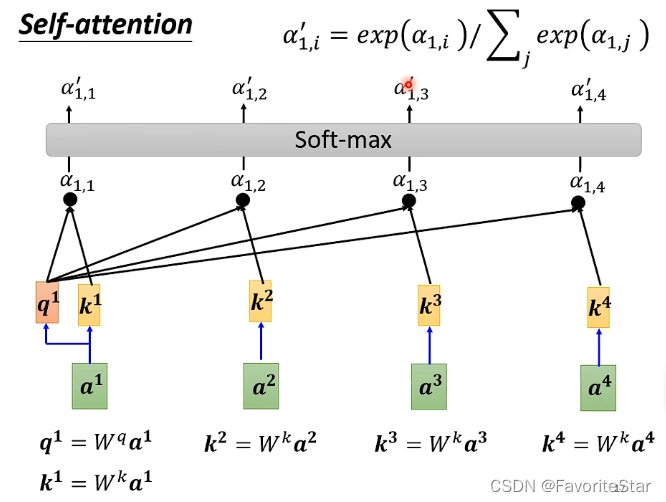
3. 對每個向量再乘以一個另外的矩陣得到一個新的向量，再進行加權和得到結果：

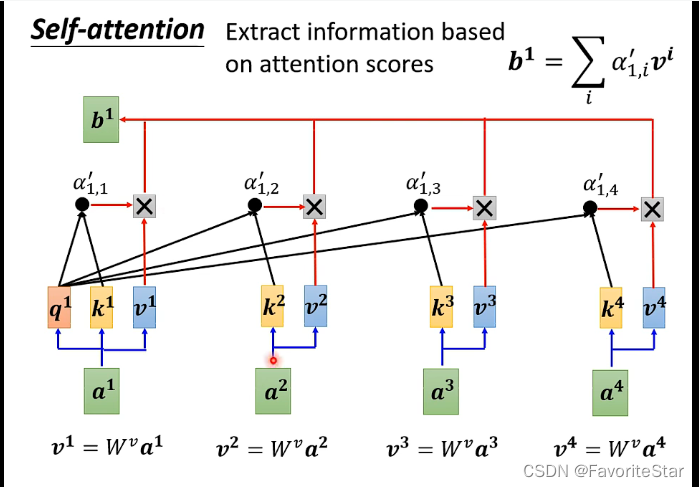
哪一個向量對應的\(\alpha\)(attention score)越大，那麼得到的b就越接近於它所計算出來的\(v\)，這就是最終結果了。

從矩陣角度理解全過程

1. 由於每一個輸入向量都需要計算\(q,k,v\)三個向量，因此可以利用矩陣的形式更加簡潔方便的進行計算：

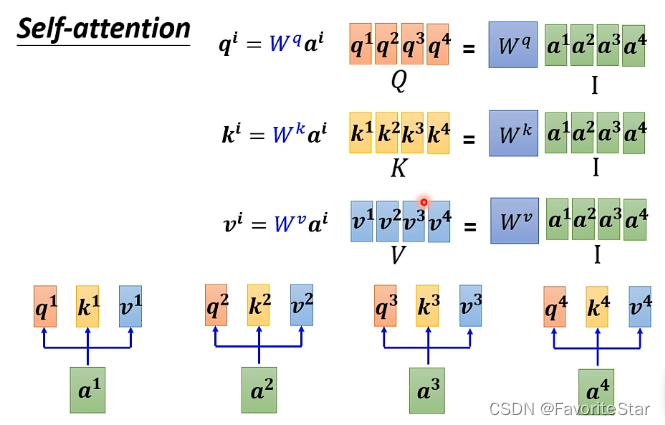
2. 計算\(\alpha\)也是同理：

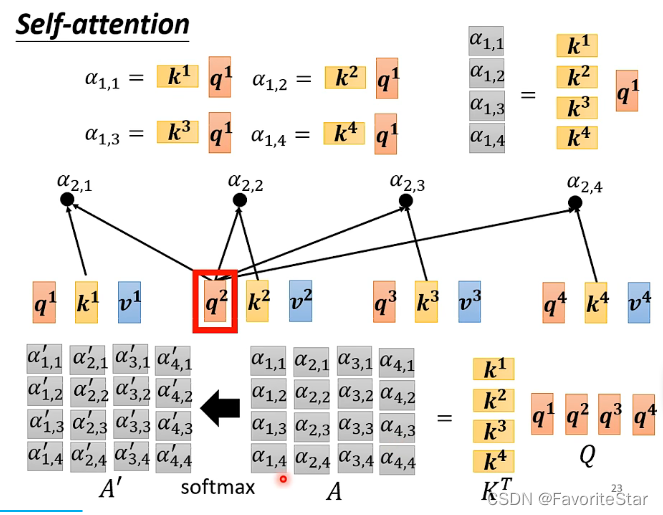
3. 計算b也是轉換成矩陣操作：

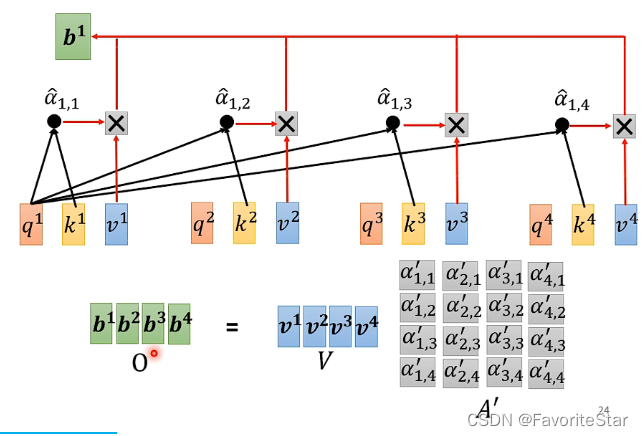
而經過上述的分析，可以看到需要學習的引數只有\(W^q,W^k,W^v\)而已。

Multi-head Self-attention

這是認為不同的輸入向量之間可能不止有一種相關性，因此：

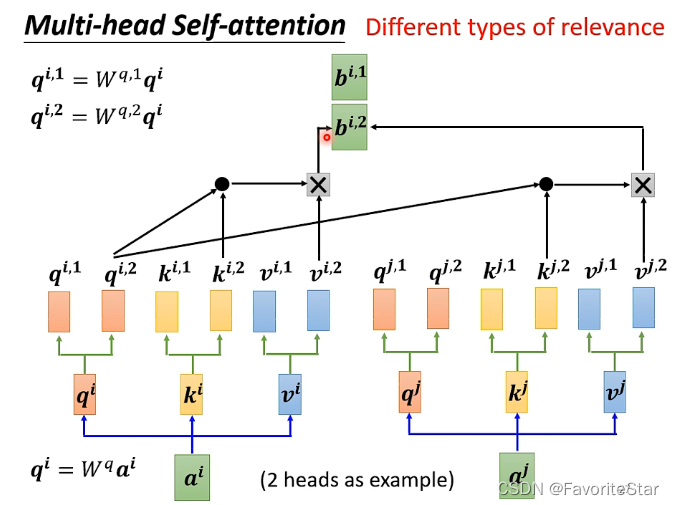
各種引數都有多重，只不過各自算各自的。

Position embedding

在前面的自注意力過程中，我們並沒有關注到各個輸入向量之間的位置資訊！這在一些場景裡面是很關鍵的一部分資訊，但是我們只是計算了各自的相關性沒有考慮到位置資訊，因此需要加上Position embedding：

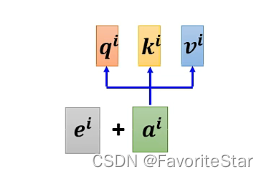
只需要在每個輸入向量上加上一個\(e^i\)即可，這個裡面就包含了具體的位置資訊，而如何產生\(e^i\)仍然是一個在研究的問題。

CNN與Self-attention

事實上，CNN是受限制的Self-attention，也就是Self-attention的特例，Self-attention可以通過某些設計和限制就可以變成CNN，完成和CNN同樣的任務。

RNN與Self-attention

RNN也是處理輸入是向量序列問題的演演算法，其具體過程就是一開始有一個memory，它和第一個輸入向量一起輸入到RNN中將會輸出一個向量，該向量一方面放入全連線網路中得到一個輸出，另一方面和下一個輸入向量一起作為下一個RNN的輸入，以此類推。

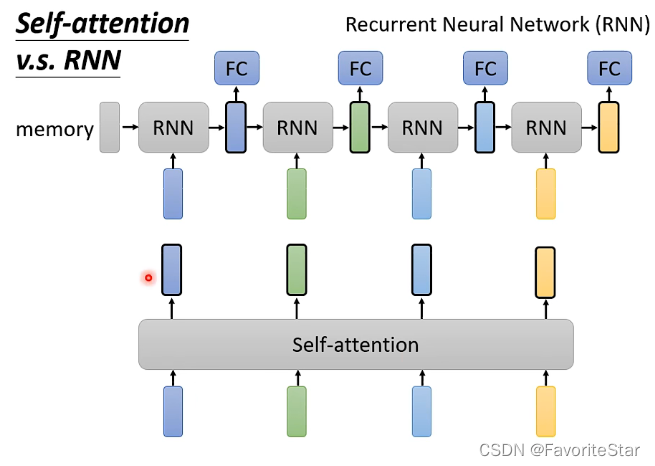
而它們的區別在於：

• 對不同位置的考慮：在RNN中如果最後一個黃色的輸出向量希望它能夠與第一個輸入的藍色向量有關，那麼就需要藍色向量從一開始輸入就一直被記得，直到最後一個；而在Self-attention則不用考慮到這個問題，計算就已經是統籌兼顧了
• 計算的平行性：RNN是無法進行平行計算的，而Self-attention是可以的。