【機器學習】李宏毅——類神經網路訓練不起來怎麼辦

如何判斷導數值為零的點的型別

當發現訓練資料集誤差不再下降的時候，不是隻有卡在區域性最小值的情況，還有另外一種情況是處於鞍點，鞍點位置處雖然其導函數為零，但是其既不是區域性最大值也不是區域性最小值，如圖：

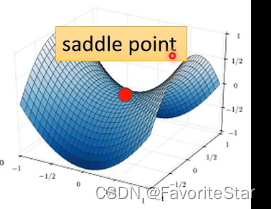
因此，我們把區域性最小值和鞍點這種點統稱為駐點（critical point），但這兩種情況是截然不同的，因為如果是區域性最小值那麼周圍都是比該點更大的loos，但是鞍點不一樣，周圍可能會有更小的loss，因此要認識到如何分辨這兩種點。

判斷導數為0的點是鞍點還是極值點

首先需要了解一下泰勒展開式，假設我們在\(\theta=\theta^{`}\)處進行二階泰勒展開（忽略冗餘項），即：

\[L(\theta)\approx L(\theta^`)+(\theta-\theta^`)g+\frac{1}{2}(\theta-\theta^`)^TH(\theta-\theta^`) \]

其中，\(g\)為梯度，是一個向量，而\(H\)是一個矩陣，存放的是L的二階微分，即：

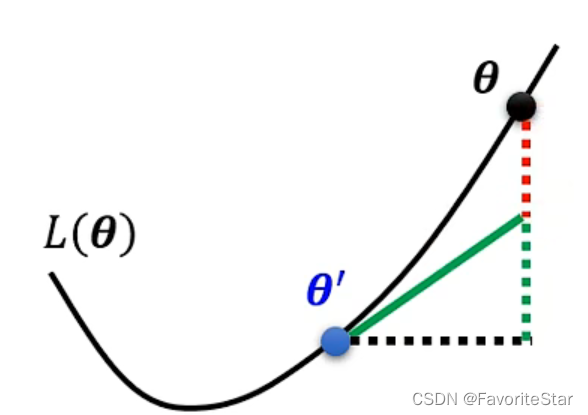
\[g=\nabla L(\theta^`)\quad g_i=\frac{\partial L(\theta^`)}{\partial \theta_i}\\ H_{ij}=\frac{\partial^2}{\partial \theta_i \partial \theta_j}L(\theta^`) \]

可以看成後面兩項就是可以補齊這兩個點之間的差距，使得值更加接近。

那麼當遇到導數值為0的點是，將會有\(g=0\)，那麼第一項為0，那麼只有第二項起作用，為了表達方便，設\(v=\theta-\theta^`\)，則若

對於任意\(v\)，均有 \(v^T Hv>0\)，則相當於在\(\theta^`\)周圍均有\(L(\theta)>L(\theta^`)\)，那麼就說明這是一個區域性最小值
對於任意\(v\)，均有 \(v^T Hv<0\)，則相當於在\(\theta^`\)周圍均有\(L(\theta)<L(\theta^`)\)，那麼就說明這是一個區域性最大值
對於任意\(v\)，有 \(v^T Hv>0\)也有 \(v^T Hv<0\)，則說明該點是一個鞍點

但是總不可能把所以的\(v\)都代進去算，因此要看矩陣\(H\)的性質！

若\(H\)為正定矩陣(positive definite)，即所有特徵值(eigen valuse)都為正，那麼就滿足區域性最小值的條件
若\(H\)為負定矩陣(negative definite)，即所有特徵值(eigen valuse)都為負，那麼就滿足區域性最大值的條件
若\(H\)的特徵值有正有負，那麼就滿足鞍點的條件

而\(H\)除了可以幫助我們判斷是什麼型別的點之外，還可以在梯度為0的情況下幫助我們判斷下一次如何更新引數，具體推導過程如下：

假設\(u\)是矩陣\(H\)的一個特徵向量，\(\lambda\)是對應的特徵值，那麼

\[u^THu=u^T(\lambda u )=\lambda \lVert u \rVert^2 \]

那麼如果\(\lambda<0\)，則這一項就小於0，那麼如果讓

\[L(\theta)=L(\theta^`) + \lambda \lVert u \rVert^2 \]

就可以讓L減小。因此只要讓\(\theta - \theta^`=u\)，則\(\theta=\theta^`+u\)就可以讓損失函數進一步減小，因此只要找出特徵值小於0對應的特徵向量，就可以繼續更新引數了。

但其實這個方法在大部分情況是不可行的，因為是二階微分的矩陣，而且求特徵值和特徵向量，這個計算量太大了。

另外一個需要補充的點是由於我們之間的視角都是二維或者三維視角，但實際上資料是特別高的維度的，因此能夠區域性最小值是非常少見的，大多數情況是一個鞍點。因為要讓海蔘矩陣的特徵值全部為正幾乎是不可能的。

批次(batch)與動量(momentum)

Batch

Batch實際上是說：在進行計算損失以及梯度時，我們並不是每次都對全部的資料計算總損失再來計算梯度，而是將資料分為許多份，每一份代表一個batch，然後每次計算一個batch中的損失再計算梯度再更新引數，每一份都計算及更新完畢稱為一個epoch，如下圖：

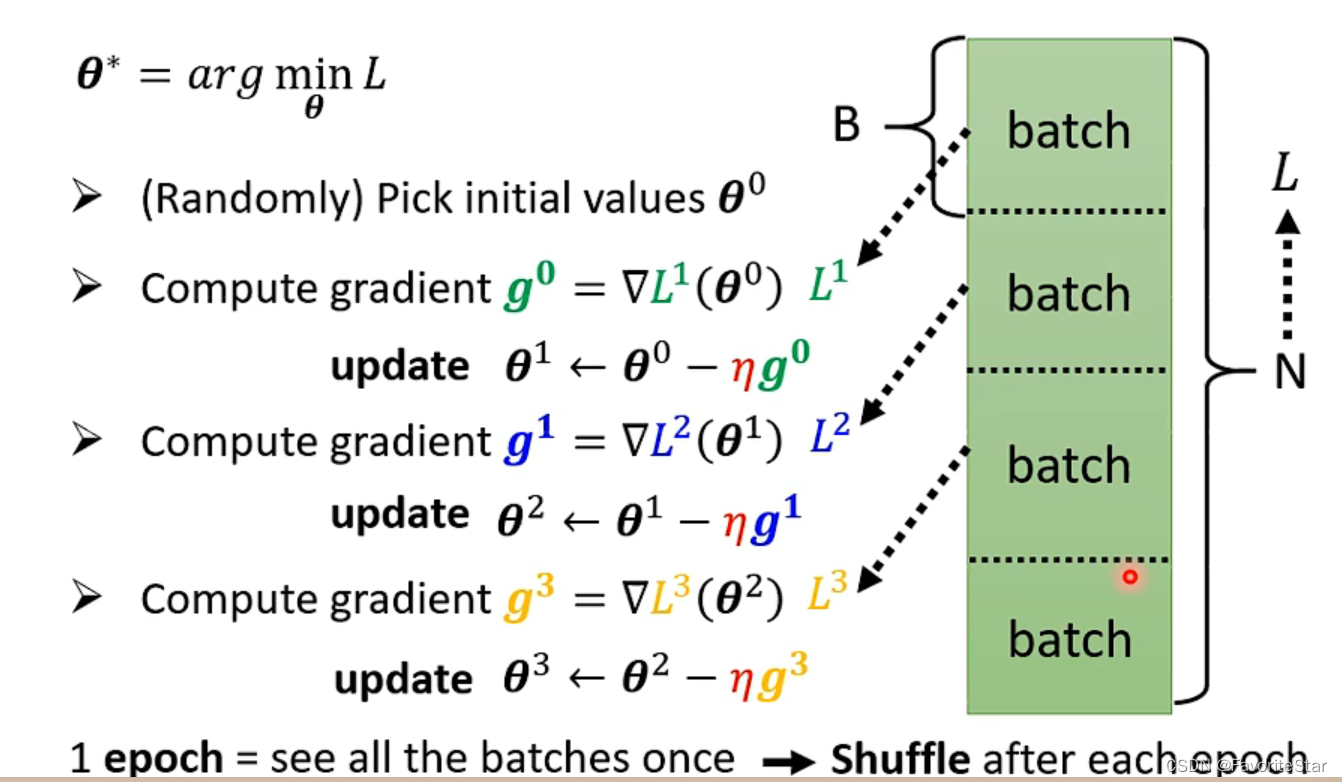
而我們可以選擇執行多次的epoch，每次都有一個shuffle過程，即重新打亂順序，重新劃分batch、

而這個batch劃分的大小就是一個值得討論的問題：

當batch更大：雖然花費時間更長，但是總體上對梯度的計算更加精確，即更新引數更加有效
當batch更小：花費時間短，但是具有一定的噪聲性質，更新的引數不一定是有效的

並且不一定batch大花費的時間就長，GPU具有平行運算的能力，在其能力範圍內batch的增加對其計算時間基本沒什麼影響。而如果計算損失和梯度的時間沒什麼太大的差距的話，那麼就會在更新引數的次數上體現出時間的差距了，如下圖：

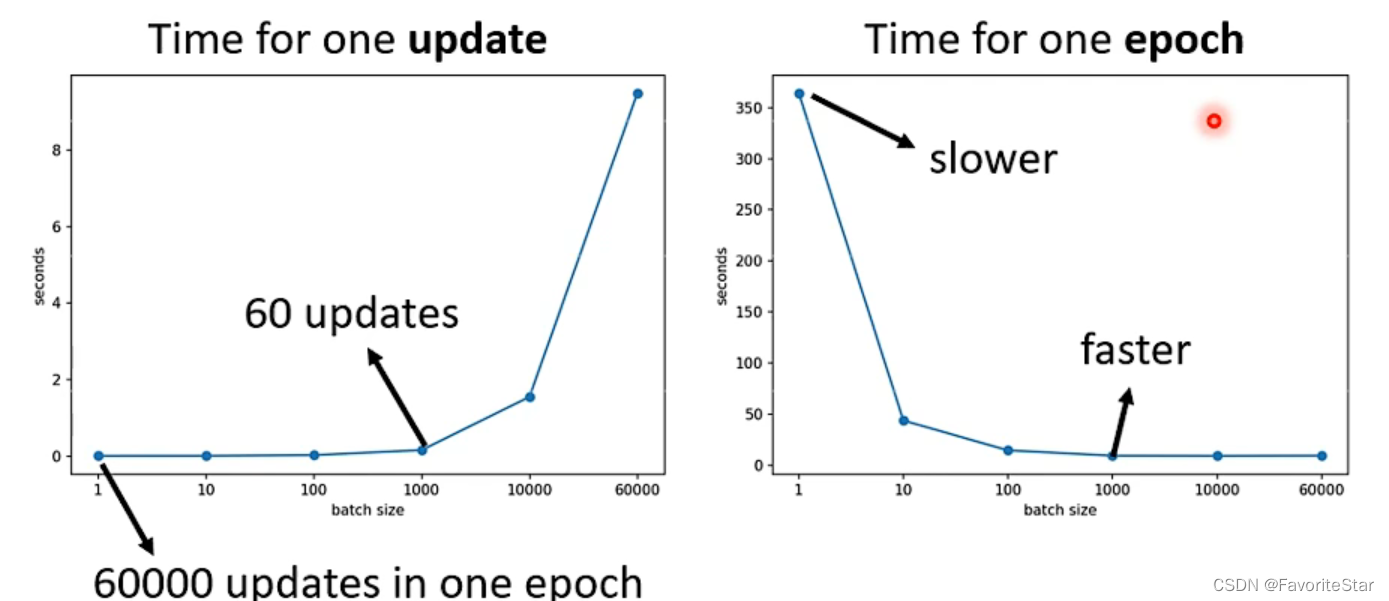
儘管batch=1能夠使得每一次更新時計算資料的速度特別快，但是由於每次epoch需要進行的更新次數太多了，因此其總體一次epoch的時間是特別長的。因此在考慮平行計算後不是batch越小越好。

那麼這樣是不是就說明越大的batch時間沒有劣勢就越好了呢？並不是！來看下圖：

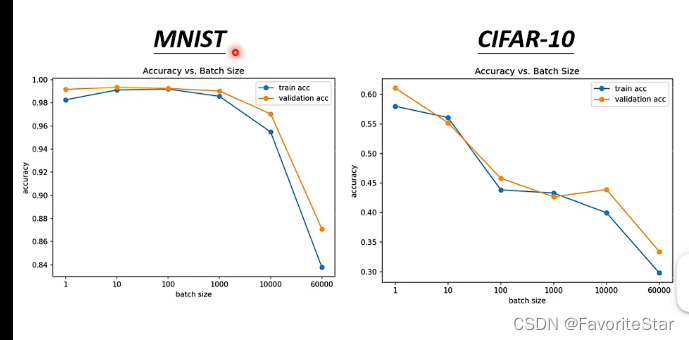
在同一個模型下，其訓練資料集的精確度居然隨著batch的增大而逐漸減小，因此這不是模型的問題，這就是batch改變而引起的優化演演算法的問題。

直觀上的解釋如下圖：

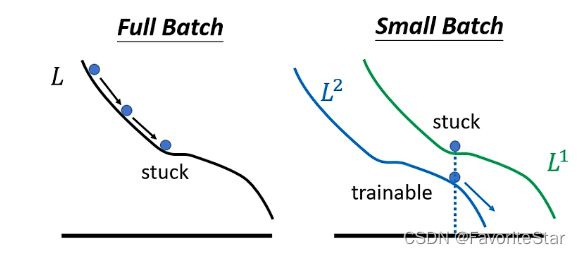
可能在整體的損失函數上陷入了區域性最小值，此時如果不考慮前述的海森矩陣的話那麼就無法繼續進行梯度更新；但是在更小的batch上可以認為每一次選用的損失函數是具有一定差異的，在L1上陷入區域性最小值那麼下一次更新的時候是L2，該點並不是區域性最小值，那麼就還可以繼續更新繼續使得損失函數降低。還有論文證明了如果在訓練集上想辦法讓大的batch和小的batch的精確度都訓練到接近一樣，但是在測試集上很可能會出現大的batch的模型的效果會差很多，如下圖：

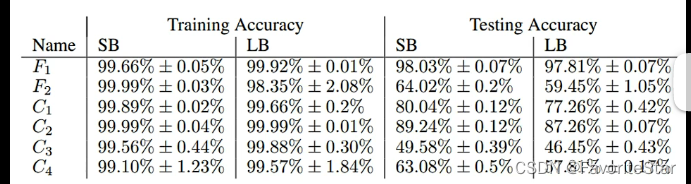
直觀上解釋可以這麼認為：

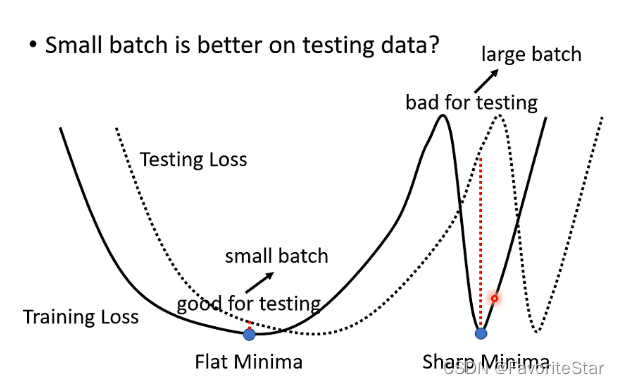
假設在訓練集的誤差函數上有兩類最小值的點，第一種Flat Minima是比較好的，另一種Sharp Minima是比較壞的，那麼對於小batch來說由於其更新引數的方向具有一定的隨機性，因此即使陷入了Sharp Minima裡面，也有較大的概率能夠更新出來，而只有在Flat Minima裡面周圍都比較平坦才能夠困住它們引數的更新；對於大batch如果陷入Sharp Minima之後幾乎就不可能出來了，因為梯度為0。那麼假設當前測試集的誤差函數是相對於訓練集的誤差函數進行移動，那麼按照剛才的說法就會導致大batch的效果很差，而小batch的效果就比較穩定。

經過上述分析，對比如下：

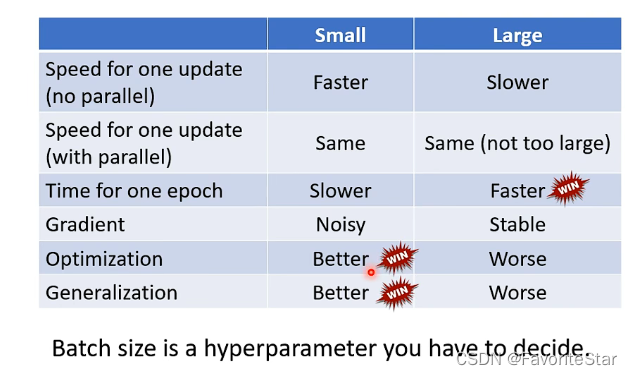
所以batch也就成為了一個需要調整的超引數。

Momentum

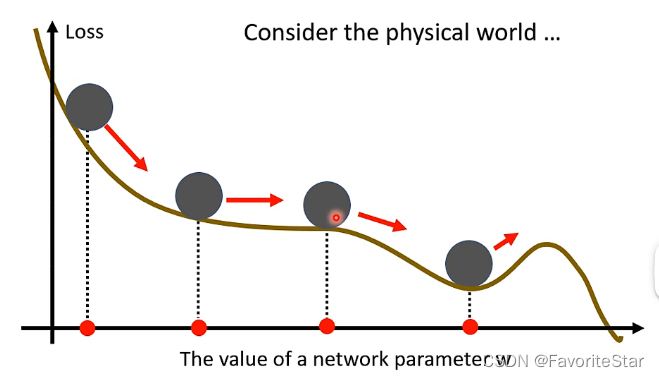
在現實生活中，如果具有動量，那麼在損失函數的下滑中是很可能不會卡在梯度為0的鞍點或者區域性最小值的，因為動量很可能會帶著他繼續往前走，因此要思考能不能加入這個動量的想法來解決駐點的問題呢？

先回顧一下梯度下降的過程：每一次引數更新的方向都是梯度的反方向

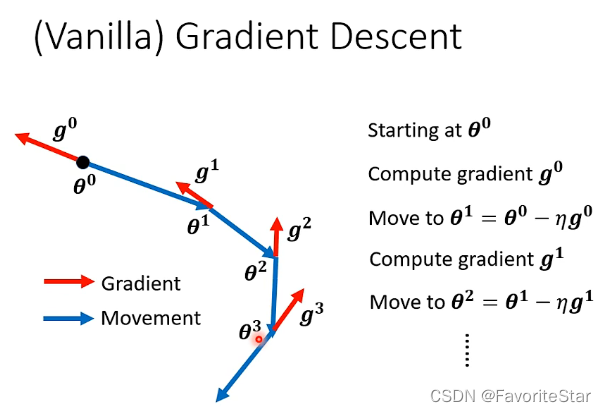
那麼如果加入了動量這個因素，則移動的方向是梯度的反方向加上前一步移動的方向這兩個綜合起來決定的。如下圖：

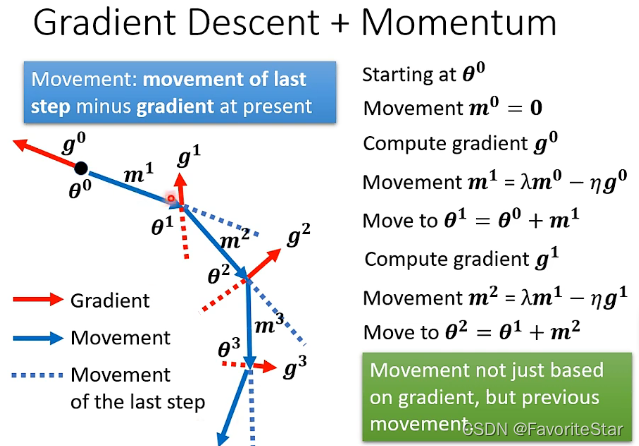
每次的方向計算為：

\[m^{t+1}=\lambda m^t - \eta g^t \]

而由於\(m^t\)與\(m^{t-1}\)和\(g^{t-1}\)有關，以此類推可以得到\(m^t\)與\(g^1\)到\(g^{t-1}\)都有關，因此另一種直觀解釋就是不只是考慮當前梯度的反方向，而是過去所有梯度方向的綜合。

自動調整學習率

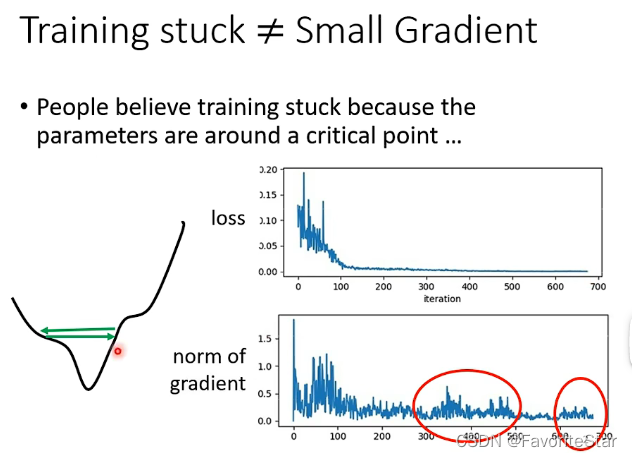
如果在訓練過程中發現訓練誤差不再下降，這可能並不是卡在了駐點的問題，這時候需要檢查一下梯度向量是否為0，如果為0，才是真正卡在了駐點的位置，但是通過下圖可以發現在後續誤差不再下降時其梯度仍然具有很大的變化，仍然不會零，但就是不能夠再誤差減小，這很可能就是在最小值的兩邊來回的震盪導致的。
,

而僅僅看上圖可能會覺得是學習率設定得太大了，那麼看下圖：

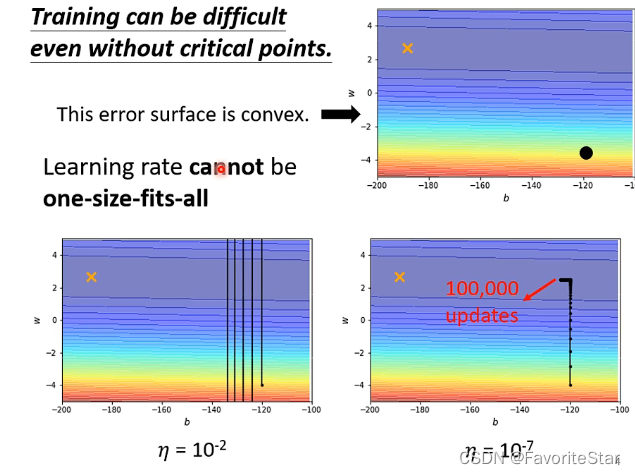
如果學習率很大，那麼極大地可能一直震盪，如果將學習率調整到足夠小，雖然它能夠進入到中間的位置然後左轉去靠近最小值的點，但是在中間部分梯度已經很小了，而你的學習率也很小，所以幾乎是不可能走完那一段路程的。因此需要自動調整學習率。

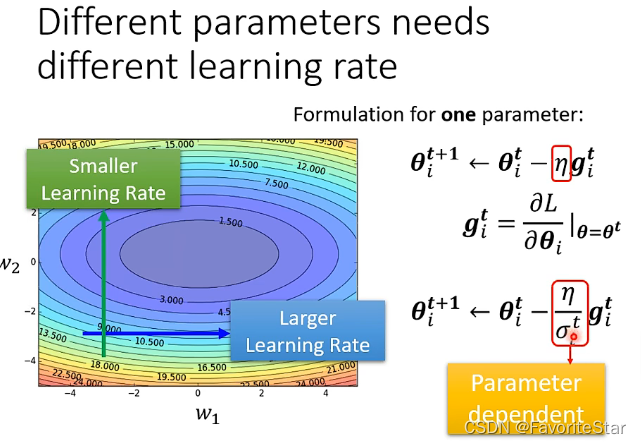
我們總希望在梯度比較小的方向上能夠有較大的學習率，在梯度比較大的方向上能夠有比較小的學習率，因此需要對每個引數客製化學習率，即：

\[\theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i}g^t|i \]

則說明現在學習率不僅與i有關而且與t有關，因此與具體的引數有關，而且也是具有迭代性質的。更新公式如下：

這為什麼能夠做到在梯度比較小的方向上能夠有較大的學習率，在梯度比較大的方向上能夠有比較小的學習率呢？如下圖：

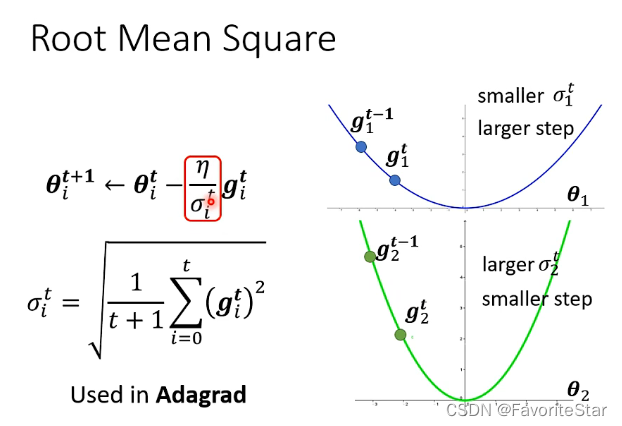
當梯度比較大，那麼\(\sigma\)算出來就大，那麼學習率就小，相反也同理。

但這個方法有一個問題，就是例如同一個引數在一開始其梯度比較大，後面的梯度比較小，但這樣前面大的梯度已經在根號裡面累積了，在梯度突然變小的時候很難讓學習率立馬反應過來而增大的，

因此改進為如下的RMSProp方法：

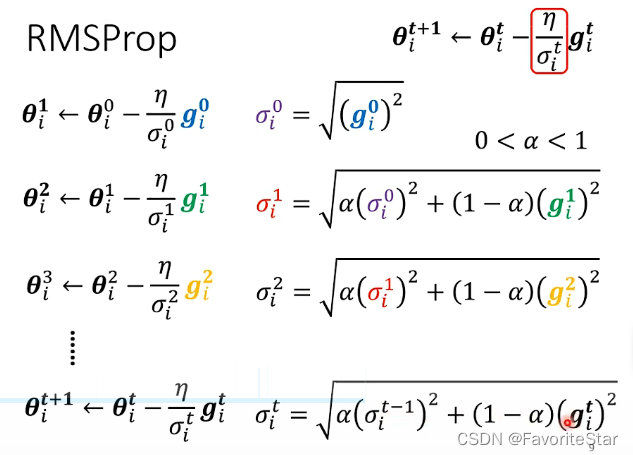
即可以手動調整權重\(\alpha\)來實時調整學習率的大小，例如下圖：

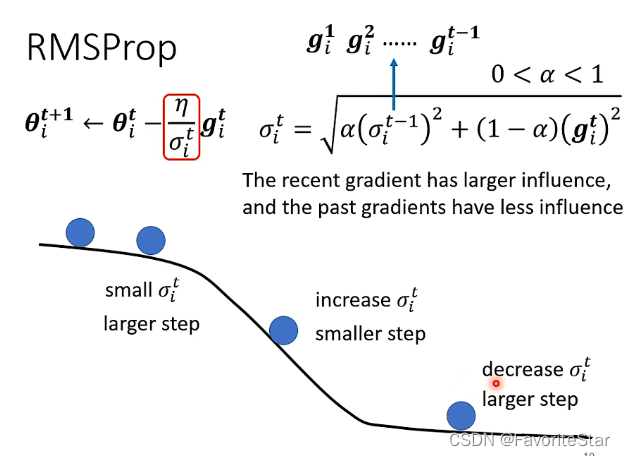
在中間滑坡的位置直接將\(\alpha\)減小，那麼學習率就會降低，從而可以慢下來；而在後面平坦的位置再將\(\alpha\)增大，那麼學習率就會增加。

因此現在較好的方法就是RMSProp+Momentum，稱為Adam

還有另外一個可以調整的地方為固定的\(\eta\)：

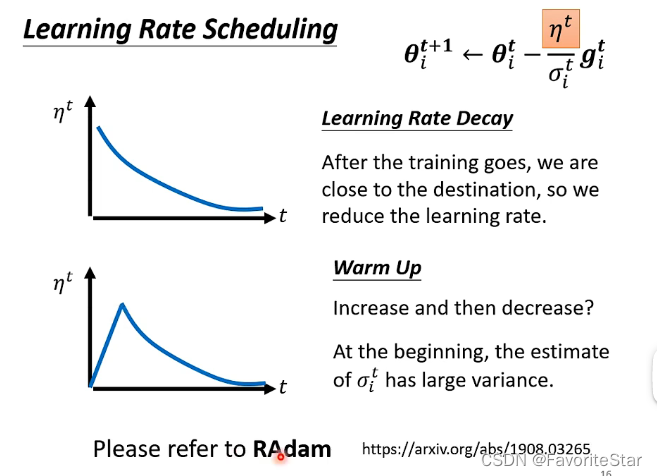
第二個方式有點難以理解，但可以這樣解釋：由於\(\sigma\)是一個累積的結果，累積一個方向的梯度有多大有多小，那麼一開始仍然處於一個摸索的階段，因此可以設定學習率比較小防止其亂飛，當累積到一定程度比較穩定之後，學習率也逐漸上升到較大的值，那麼再穩定移動，此時再來慢慢減小。

那麼結合上述的方法可以使用這種方法：

但有一個疑問就是\(m^t_i\)和\(\sigma^t_i\)會不會相互抵消，其實是不會的，因為m雖然考慮了所有的梯度，但是也考慮了它們的方向以及正負，而\(\sigma\)是將各個梯度的平方求和再開根號，所有並不會有抵消的作用。

損失函數的影響

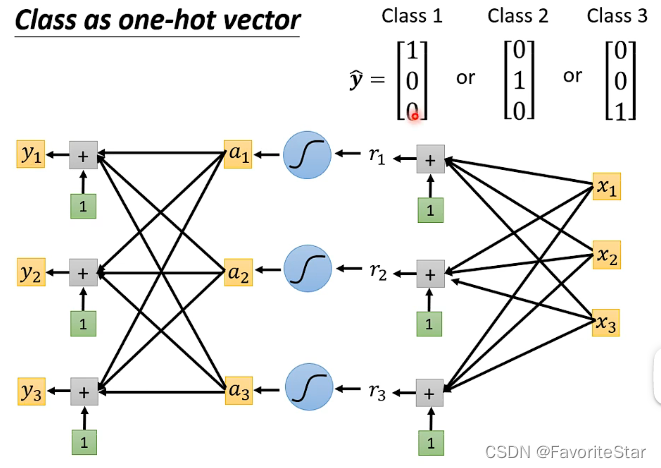
對於分類問題，也可以用迴歸的模型，只需要將輸出改為一個向量即可。

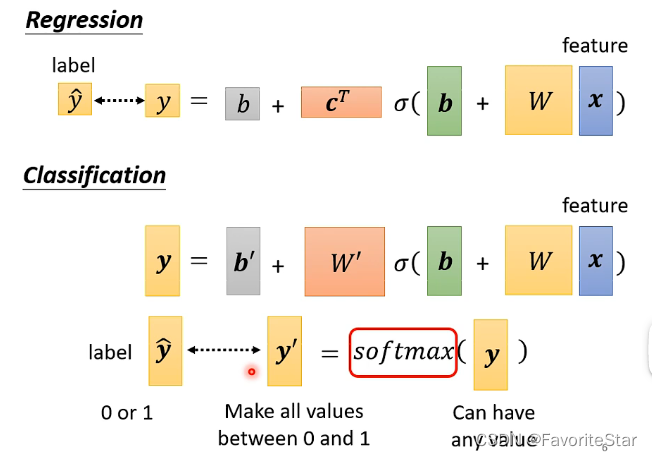
且一般來說，對於用模型計算出來的y，通常是加上一個softmax函數處理之後，再來跟理想\(\hat{y}\)進行對比相似度的。

softmax的處理過程如下：

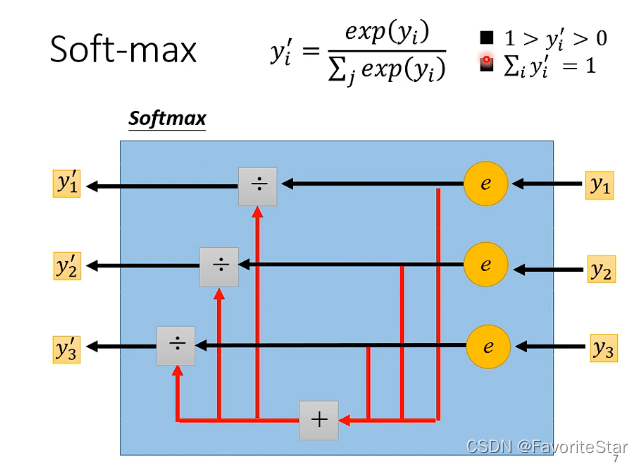
而上述的例子是三個類別，雖然softmax也可以運用在兩個類別的問題上，但更多在面對兩個類別的問題時是利用Sigmoid函數，，不過在兩個類別時這兩種方法是等價的。

而在比較\(y`\)和\(\hat{y}\)時，也有幾種方法，例如：

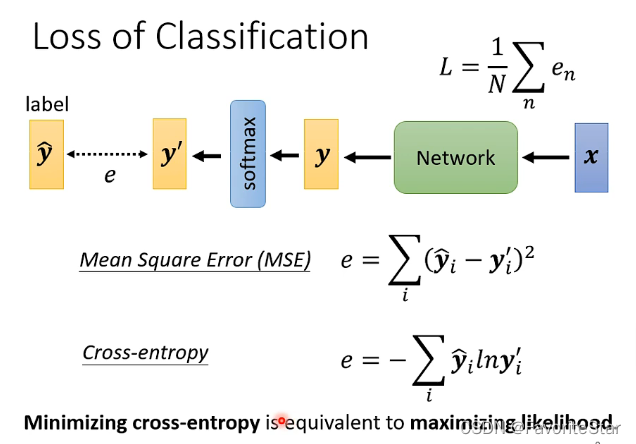
需要知道的是最大可能性和最小化交叉熵是等價的。

下面通過一個例子來表明這兩種損失函數的區別：在兩張圖中都可以看到，在右下角都是\(y_1\)大而\(y_2\)小，那麼損失函數都很小，左上角都是\(y_1\)小而\(y_2\)大，暗惡魔損失韓式都很大，這就很滿足我們的預期

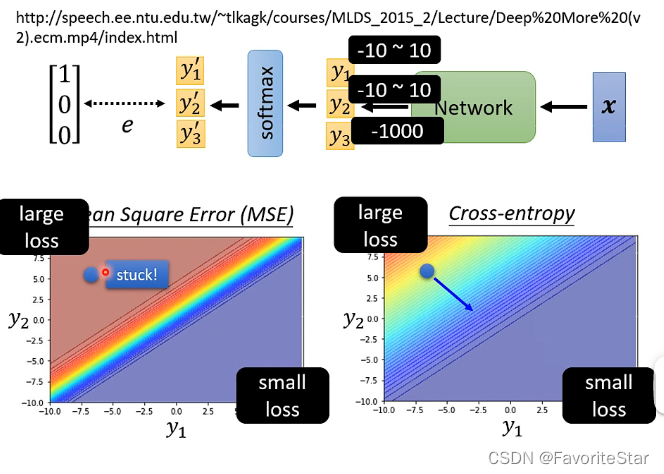
但在MSE的損失函數中，如果訓練的起點位於左上方的損失函數很大的位置，其很明顯的特性在於其是非常平坦的，梯度很小，大面積都很大的損失，因此訓練起來就很難走往右下角，而在交叉熵中就不會有這個問題。因此在分類問題中要用交叉熵作為損失函數。