前言

B樹（B-tree），也常被記作 B-樹，其中「-」不發音。B樹的發明者 Rudolf Bayer 和 Edward M. McCreight 並沒有給B樹中的 B 明確的定義，大家也不必對此糾結太多。

B+樹是B樹的變體，兩者的適用場景是不一樣的，以後也會給大家帶來B+樹的介紹。

本系列將用三篇文章講解B樹的設計理念及如何用 C# 實現一個記憶體版本的B樹：

B樹的定義及資料的插入（本文）
資料的讀取及遍歷
資料的刪除

完整程式碼已放至github https://github.com/eventhorizon-cli/EventHorizon.BTree
或者安裝 nuget 包進行體驗

dotnet add package EventHorizon.BTree

完整程式碼中包含了debug輔助程式碼，可以通過偵錯來了解B樹的內部結構。

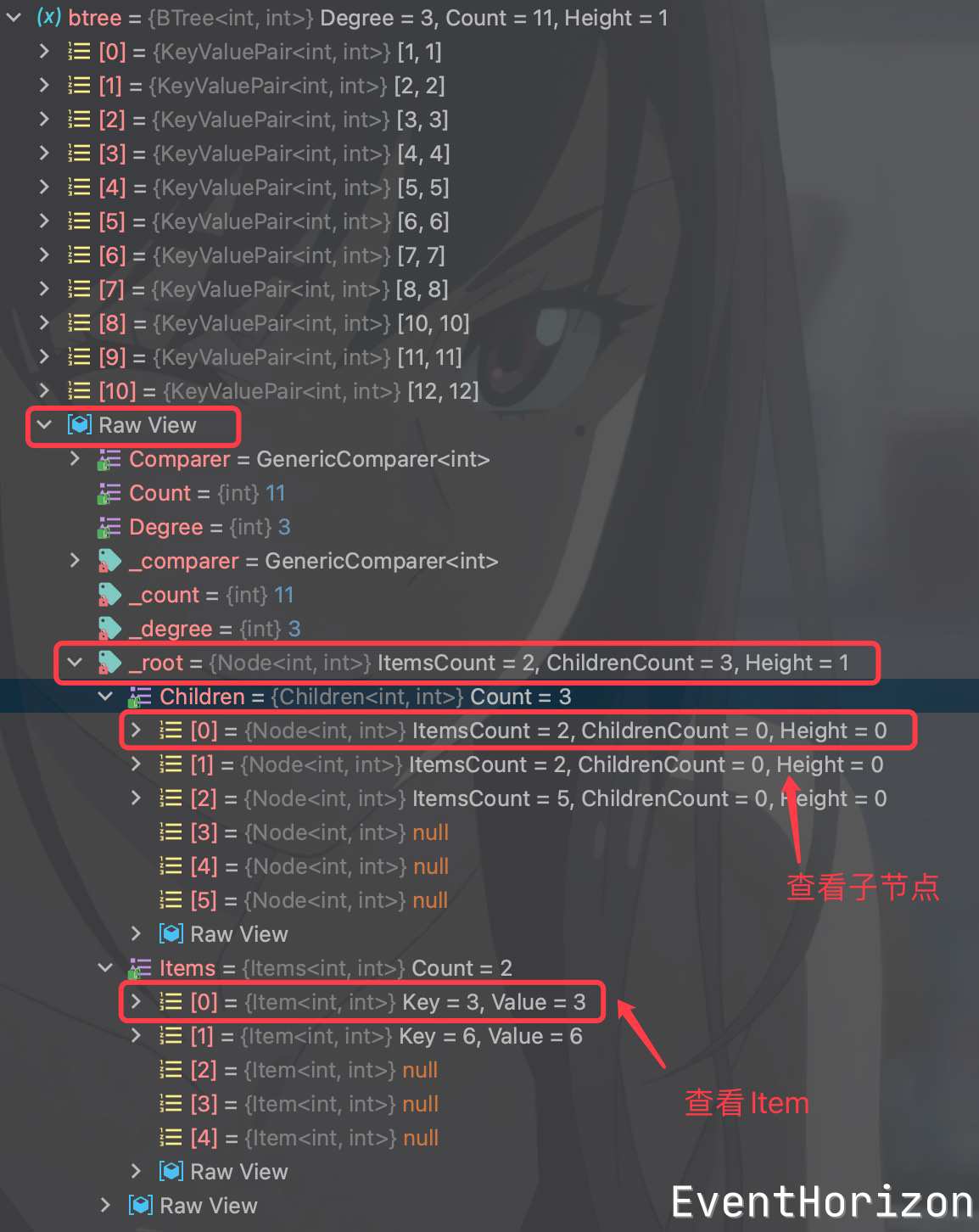
B樹最早被設計出來，並不是作為一個單純的記憶體資料結構，而是用作 磁碟儲存引擎 的索引實現，以後也會單獨寫一篇文章來做說明。

本文部分說明參照自PingCAP 的公開ppt 寶寶床邊故事集：儲存引擎，強烈推薦給各位學習。

部分內容屬於個人理解，若有不對之處，歡迎指正。

索引原理

區域性性（Locality）

硬體、作業系統等等系統，絕大部分時候，執行一次操作流程有額外的開銷（overhead）。

因此很多部件、模組都設計成：連續執行類似或相同的操作、存取空間相鄰的內容時，則將多次操作合併為一次，或多次之間共用上下文資訊。這樣能極大提升效能。

這種時間、空間上的連續性，叫做區域性性。

資料的區域性性

我們把資料的連續性及連續區域大小稱為 區域性性，連續存放的資料越多，區域性性越好。

記憶體儲存和磁碟儲存

IO的存取效能有兩個重要的衡量指標：

IOPS(Input/Output Operations Per Second)：每秒進行IO讀寫操作的次數
IOBW(Input/Output Bandwidth)： IO頻寬

磁碟的IOPS和IOBW都低於記憶體，IOPS更為明顯。

磁碟IO是以頁（page）為單位進行資料讀取的，如果資料的區域性性好，只載入一個磁碟頁到記憶體就可以實現一組有序資料的連續存取。如果資料的區域性性差，則每讀取一次資料都有可能要載入一個磁碟頁，效能較差。

當資料區域性性差時：

需要更頻繁地存取磁碟
IOPS 比 IOBW 先達到上限，效能差

當資料區域性性好時：

IOBW 能達到硬體上限
IOBW 達到上限是理想的最好效能

磁碟儲存適合的索引結構

綜上所述，就磁碟儲存而言，區域性性的好壞對效能影響很大。

有序陣列的區域性性很好，用二分查詢法查詢資料的時間複雜度是O(log n)。但插入資料時，時間複雜度就成了O(n)。

二叉平衡樹（Self-balancing binary search tree，常見的實現如 AVL樹和紅黑樹）用二分查詢法查詢資料的時間複雜度是O(log n)。插入資料時也是先查詢到具體位置，時間複雜度是O(log n)。

但二叉平衡樹的區域性性很差，這在記憶體中不是什麼問題，因為記憶體存取亂資料的效能很高，但在磁碟中，不斷載入不同的磁碟頁，overhead 很高。

資料的區域性性越好，讀效能更好，但寫效能會降低。
資料的區域性性越差，讀效能會變差，但寫效能會更好。

B樹則是在這兩者之間尋求平衡點：

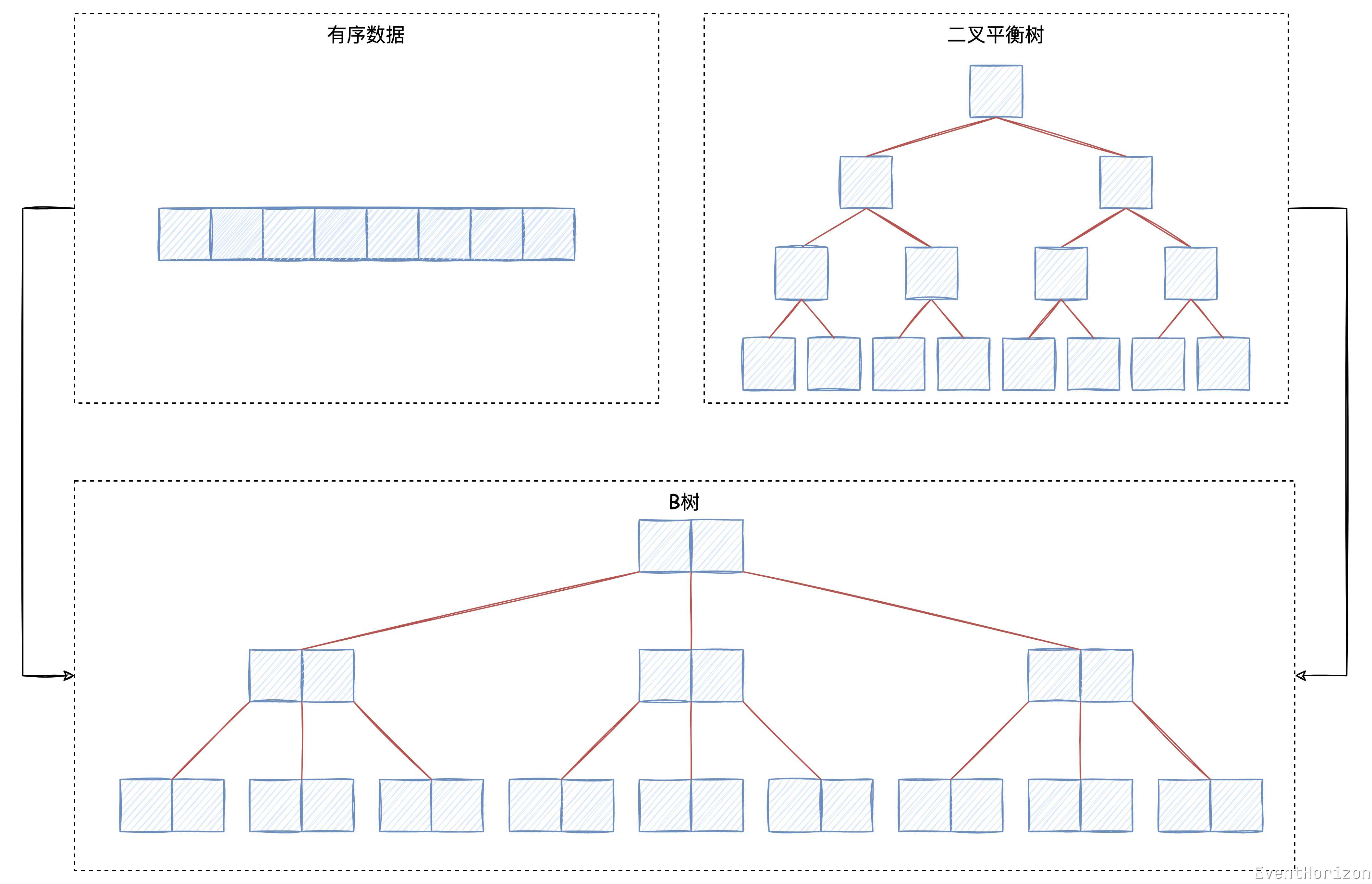
從有序陣列的角度看，我們把大陣列分割成了一個個小的有序陣列，再用另一種有序結構把小陣列組織起來，插入資料時，行動資料量減少並且可控。

從樹的角度看，用一個個小的有序陣列代替元素作為節點，大大增加了區域性性，減少了儲存 overhead。

B樹簡介

定義

B樹中的節點分為三種：

根節點（root node）
內部節點（internal node）：儲存資料以及指向其子節點的指標。
葉子節點（leaf node）：葉子節點只儲存資料，沒有子節點。

B樹只有一個節點時，根節點本身就是葉子節點。

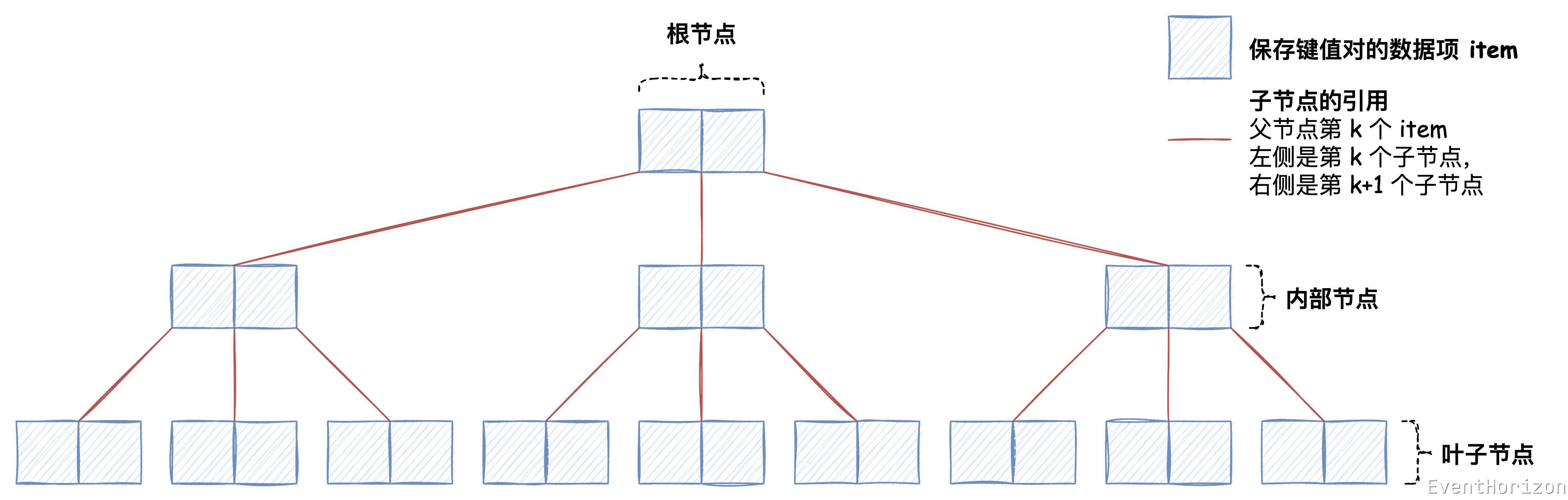
節點中每一個資料項（下文用 item 代替）都是一組鍵值對。item 的數量範圍需要預定義，通常有以下兩種定義方式：

度（degree）：通常簡寫為 t，2t-1 代表 item 數量上限。
階（order）：通常簡寫為 m，m 代表 item 數量上限。

本文用度（degree）進行描述，一個度是 t（t>=2）的B樹被設計為具有以下屬性：

每一個節點最多有 2t 個子節點。
每一個內部節點最少有 t 個子節點。
如果根節點不是葉子節點，那麼它至少有兩個子節點。
有 k 個子節點的非葉子節點擁有 k − 1 個鍵。
所有的葉子節點都在同一層。

這5個屬性都是為了維持B樹的平衡。其中前4個是在度被定義後就可以控制的，而第5個是源於B樹新增資料的方式，稍後會做解釋。

B樹中資料的有序性

每個節點中的 Item 按 Key 有序排列（規則可以是自定義的）。
升序排序時，每個 Item 左子樹中的 Item 的 Key 均小於當前 Item 的 Key。
升序排序時，每個 Item 右子樹中的 Item 的 Key 均大於當前 Item 的 Key。

用C#定義資料結構

開始演演算法講解前，我們需要先定義下將會用到的資料結構。

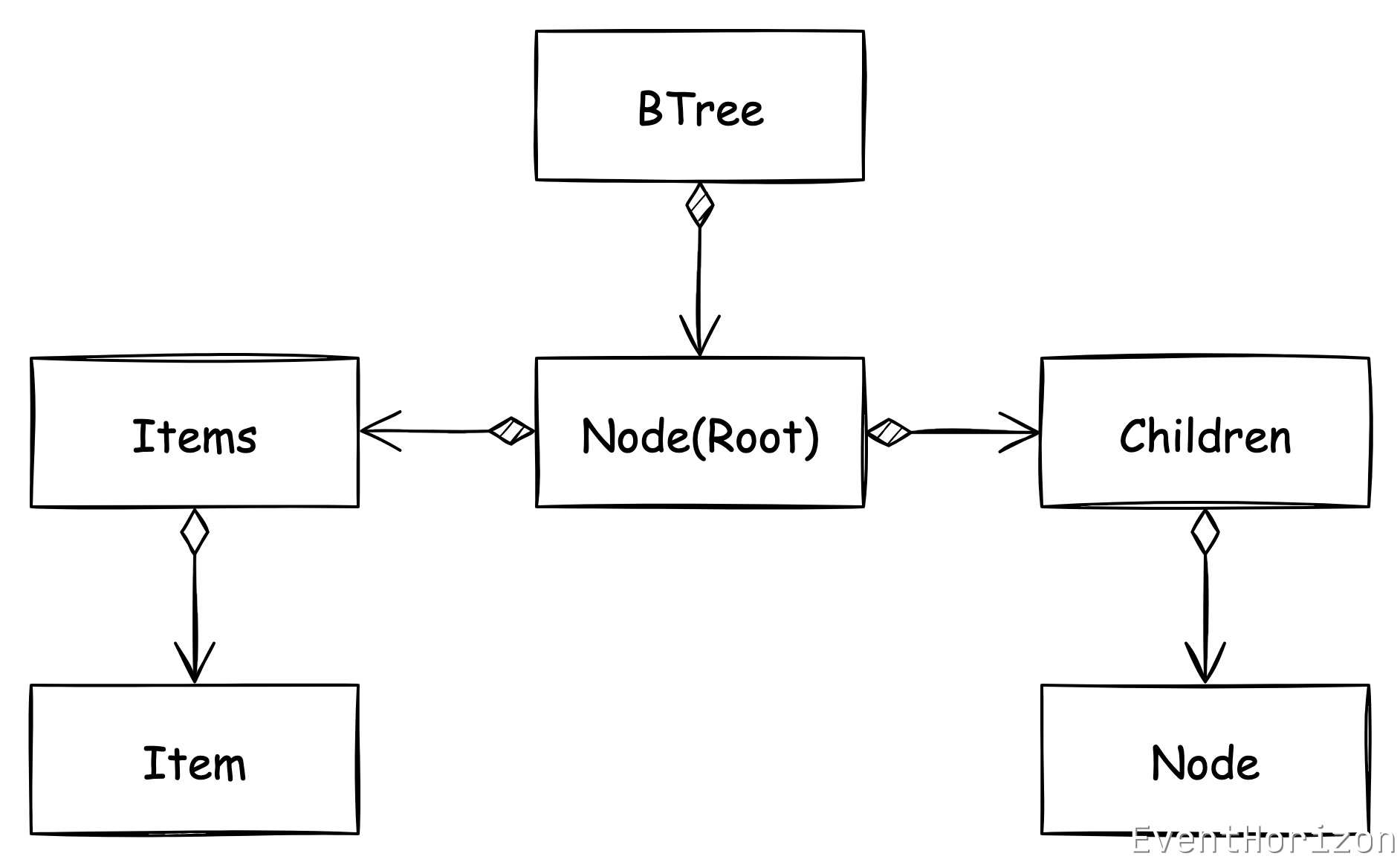
雖然程式碼太多可能影響閱讀體驗，但考慮到 gayhub 可能存取不穩定，還是儘量貼全了。

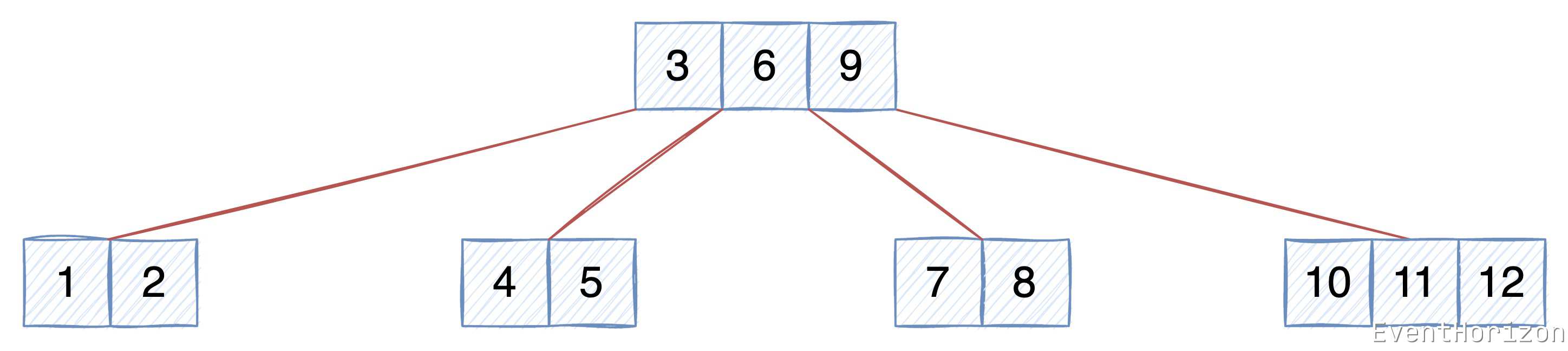
下圖所示是一個 degree 是 3 的 B樹，Key 按升序排序。

internal class Item<TKey, TValue>
{
    #region Constructors

    public Item(TKey key, TValue? value)
    {
        Key = key;
        Value = value;
    }

    #endregion

    #region Properties

    public TKey Key { get; }

    public TValue? Value { get; set; }
    
    #endregion
}

定義 Items 和 Children 兩個型別分別用於儲存 Item 集合和子節點集合。為了簡化設計以及減少動態擴容帶來的效能損失，作為資料實際容器的陣列在第一開始就會按最大的 capacity 進行建立。同時也預先給 Items 和 Children 定義好後面會被用到的基本方法。

internal class Items<TKey, TValue>
{
    #region Fields

    private readonly Item<TKey, TValue?>?[] _items;
    private readonly int _capacity;
    private readonly IComparer<TKey> _comparer;

    private int _count;

    #endregion

    #region Constructors

    public Items(int capacity, IComparer<TKey> comparer)
    {
        _capacity = capacity;
        _items = new Item<TKey, TValue?>[capacity];
        _comparer = comparer;
    }

    #region Properties

    public int Count => _count;

    #endregion

    #region Indexers

    public Item<TKey, TValue?> this[int index]
    {
        get
        {
            if (index < 0 || index >= _count)
            {
                throw new IndexOutOfRangeException();
            }

            return _items[index]!;
        }
        set => _items[index] = value;
    }

    #endregion

    #endregion

    #region Public Methods

    /// <summary>
    /// 查詢指定的鍵，並返回它的索引，如果找不到則返回key可以插入的位置
    /// </summary>
    /// <param name="key">指定的key</param>
    /// <param name="index">key的索引或者其可以插入的位置</param>
    /// <returns>指定的key是否存在</returns>
    public bool TryFindKey(TKey key, out int index)
    {
        if (_count == 0)
        {
            index = 0;
            return false;
        }

        // 二分查詢
        int left = 0;
        int right = _count - 1;
        while (left <= right)
        {
            int middle = (left + right) / 2;
            var compareResult = _comparer.Compare(key, _items[middle]!.Key);
            if (compareResult == 0)
            {
                index = middle;
                return true;
            }

            if (compareResult < 0)
            {
                right = middle - 1;
            }
            else
            {
                left = middle + 1;
            }
        }

        index = left;
        return false;
    }

    public void InsertAt(int index, Item<TKey, TValue?> item)
    {
        if (_count == _capacity)
            throw new InvalidOperationException("Cannot insert into a full list.");

        if (index < _count)
            Array.Copy(_items, index, _items, index + 1, _count - index);

        _items[index] = item;
        _count++;
    }

    public void Add(Item<TKey, TValue?> item) => InsertAt(_count, item);

    public void AddRange(Items<TKey, TValue?> items)
    {
        if (_count + items.Count > _capacity)
            throw new InvalidOperationException("Cannot add items to a full list.");

        Array.Copy(items._items, 0, _items, _count, items.Count);
        _count += items.Count;
    }

    public Item<TKey, TValue?> RemoveAt(int index)
    {
        if (index >= _count)
            throw new ArgumentOutOfRangeException(nameof(index));

        var item = _items[index];

        if (index < _count - 1)
            Array.Copy(_items, index + 1, _items, index, _count - index - 1);

        _items[_count - 1] = null;
        _count--;

        return item!;
    }


    public Item<TKey, TValue?> RemoveLast() => RemoveAt(_count - 1);

    public void Truncate(int index)
    {
        if (index >= _count)
            throw new ArgumentOutOfRangeException(nameof(index));

        for (int i = index; i < _count; i++)
        {
            _items[i] = null;
        }

        _count = index;
    }

    #endregion
}

internal class Children<TKey, TValue>
{
    #region Fields

    private readonly Node<TKey, TValue?>?[] _children;
    private readonly int _capacity;

    private int _count;

    #endregion

    #region Constructors

    public Children(int capacity)
    {
        _capacity = capacity;
        _children = new Node<TKey, TValue?>[_capacity];
    }

    #endregion

    #region Properties

    public int Count => _count;

    #endregion

    #region Indexers

    public Node<TKey, TValue?> this[int index]
    {
        get
        {
            if (index < 0 || index >= _count)
            {
                throw new IndexOutOfRangeException();
            }

            return _children[index]!;
        }
    }

    #endregion

    #region Public Methods

    public void InsertAt(int index, Node<TKey, TValue?> child)
    {
        if (_count == _capacity)
            throw new InvalidOperationException("Cannot insert into a full list.");

        if (index < _count)
            Array.Copy(_children, index, _children, index + 1, _count - index);

        _children[index] = child;
        _count++;
    }

    public void Add(Node<TKey, TValue?> child) => InsertAt(_count, child);

    public void AddRange(Children<TKey, TValue?> children)
    {
        if (_count + children.Count > _capacity)
            throw new InvalidOperationException("Cannot add to a full list.");

        Array.Copy(children._children, 0, _children, _count, children.Count);
        _count += children.Count;
    }

    public Node<TKey, TValue?> RemoveAt(int index)
    {
        if (index >= _count)
            throw new ArgumentOutOfRangeException(nameof(index));

        var child = _children[index];

        if (index < _count - 1)
            Array.Copy(_children, index + 1, _children, index, _count - index - 1);

        _children[_count - 1] = null;
        _count--;

        return child!;
    }

    public Node<TKey, TValue?> RemoveLast() => RemoveAt(_count - 1);

    public void Truncate(int index)
    {
        if (index >= _count)
            throw new ArgumentOutOfRangeException(nameof(index));

        for (var i = index; i < _count; i++)
            _children[i] = null;

        _count = index;
    }

    #endregion
}

用 Node 來表示每個節點，支援傳入 Comparer 用於實現自定義的排序方式。

internal class Node<TKey, TValue>
{
    #region Fields

    private readonly IComparer<TKey> _comparer;
    private readonly int _degree;
    private readonly int _minItems;
    private readonly int _maxItems;
    private readonly int _maxChildren;

    private readonly Items<TKey, TValue?> _items;
    private readonly Children<TKey, TValue?> _children;

    #endregion

    #region Constructors

    public Node(int degree, IComparer<TKey> comparer)
    {
        _degree = degree;
        _comparer = comparer;
        _minItems = degree - 1;
        _maxItems = 2 * degree - 1;
        _maxChildren = 2 * degree;

        _items = new Items<TKey, TValue?>(_maxItems, _comparer);
        _children = new Children<TKey, TValue?>(_maxChildren);
    }

    #endregion

    #region Properties

    public int ItemsCount => _items.Count;

    public int ChildrenCount => _children.Count;

    public bool IsItemsFull => ItemsCount == _maxItems;
    public bool IsItemsEmpty => ItemsCount == 0;

    public bool IsLeaf => ChildrenCount == 0;

    #endregion

    // ...
}

public sealed class BTree<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue?>>
{
    #region Fields

    private readonly int _degree;
    private readonly IComparer<TKey> _comparer;
    private int _count;
    private Node<TKey, TValue?>? _root;

    #endregion

    #region Constructors

    public BTree(int degree) : this(degree, Comparer<TKey>.Default)
    {
    }

    public BTree(int degree, IComparer<TKey> comparer)
    {
        if (degree < 2)
        {
            throw new ArgumentOutOfRangeException(nameof(degree), "Degree must be at least 2.");
        }

        ArgumentNullException.ThrowIfNull(comparer);

        _degree = degree;
        _comparer = comparer;
    }

    #endregion

    #region Properties

    public int Count => _count;

    public int Degree => _degree;

    public IComparer<TKey> Comparer => _comparer;

    #endregion

    // ...
}

插入資料的過程

先重複一下上文提到的B樹的順序特性：

每個節點中的 Item 按 Key 有序排列（規則可以是自定義的）。
升序排序時，每個 Item 左子樹中的 Item 的 Key 均小於當前 Item 的 Key。
升序排序時，每個 Item 右子樹中的 Item 的 Key 均大於當前 Item 的 Key。

插入資料的過程就是在樹中找到合適的位置插入資料，同時保證樹的順序特性不變。

尋找位置的過程是遞迴的，從根節點開始，如果當前節點是葉子節點，那麼就在當前節點中插入資料；如果當前節點不是葉子節點，那麼就根據當前節點中的 Item 的 Key 和要插入的資料的 Key 的大小關係，決定是向左子樹還是右子樹繼續尋找合適的位置。

以下面這個圖例來說明插入資料的過程：

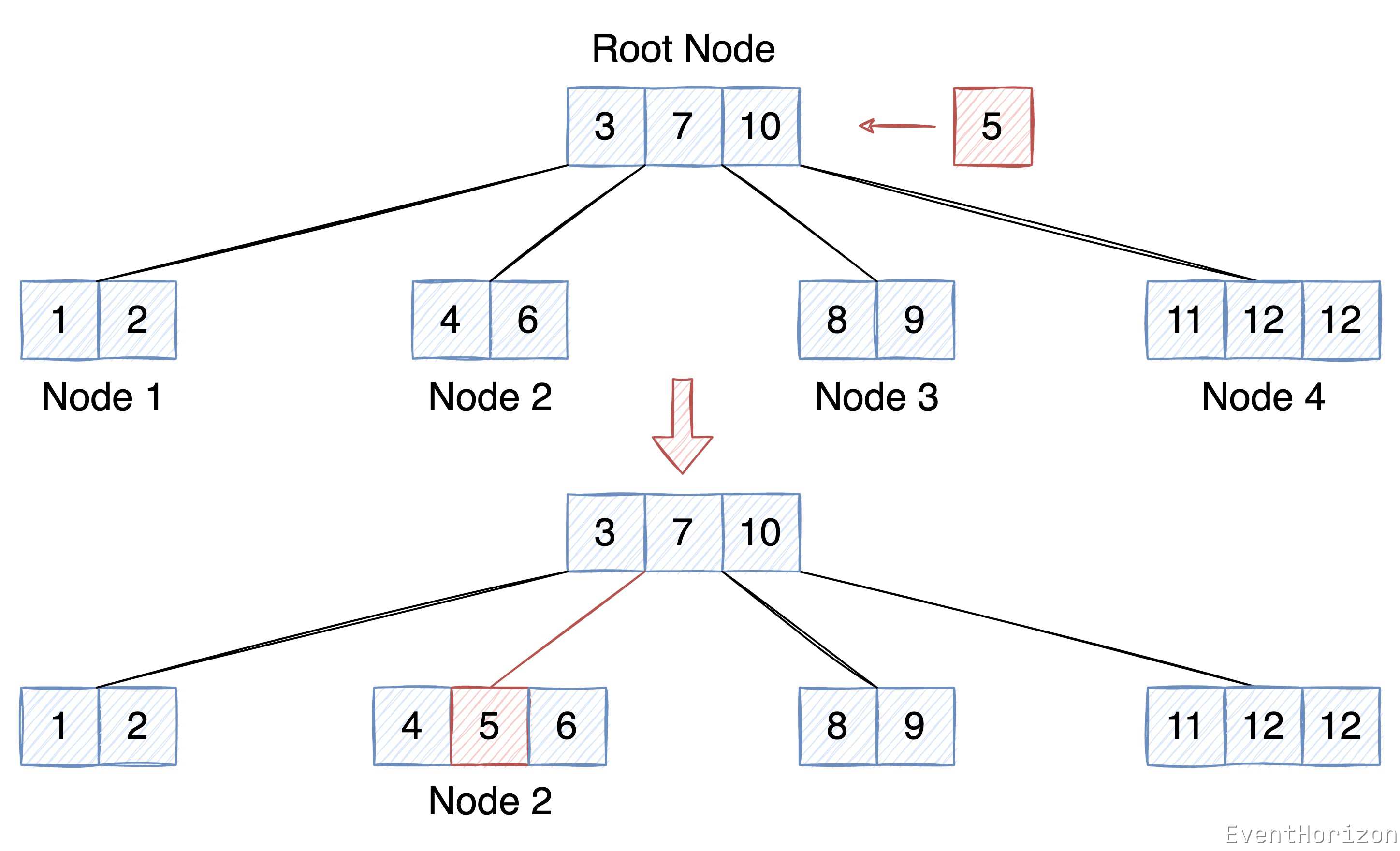
在根節點中，藉助二分查詢法找到 5 的位置應該在 3 和 7 之間，因為根節點不是葉子節點，所以不能在根節點直接插入，繼續在 Node 2 中尋找合適的位置。Node 2 是 3 的右子樹，7 的左子樹，其中的 Key 都大於 3，小於 7。
Node 2 是葉子節點，所以可以在 Node 2 中插入 5。按二分查詢法找到 5 的位置應該在 4 和 6 之間，所以插入資料後 Node 2 中的 Item 應該是這樣的：[4, 5, 6]。

分裂：新節點誕生的唯一方式

上文提到單個節點最多隻能有 2t-1 個 Item，如果節點已經滿了，還有新 Item 需要插入的話，節點就需要進行分裂。

根節點的分裂

如果根節點滿了（Item的數量達到2t-1），有需要插入新 Item 的話，就需要對根節點進行分裂，分裂後的根節點會有兩個子節點，分別是原來的根節點和新的節點。

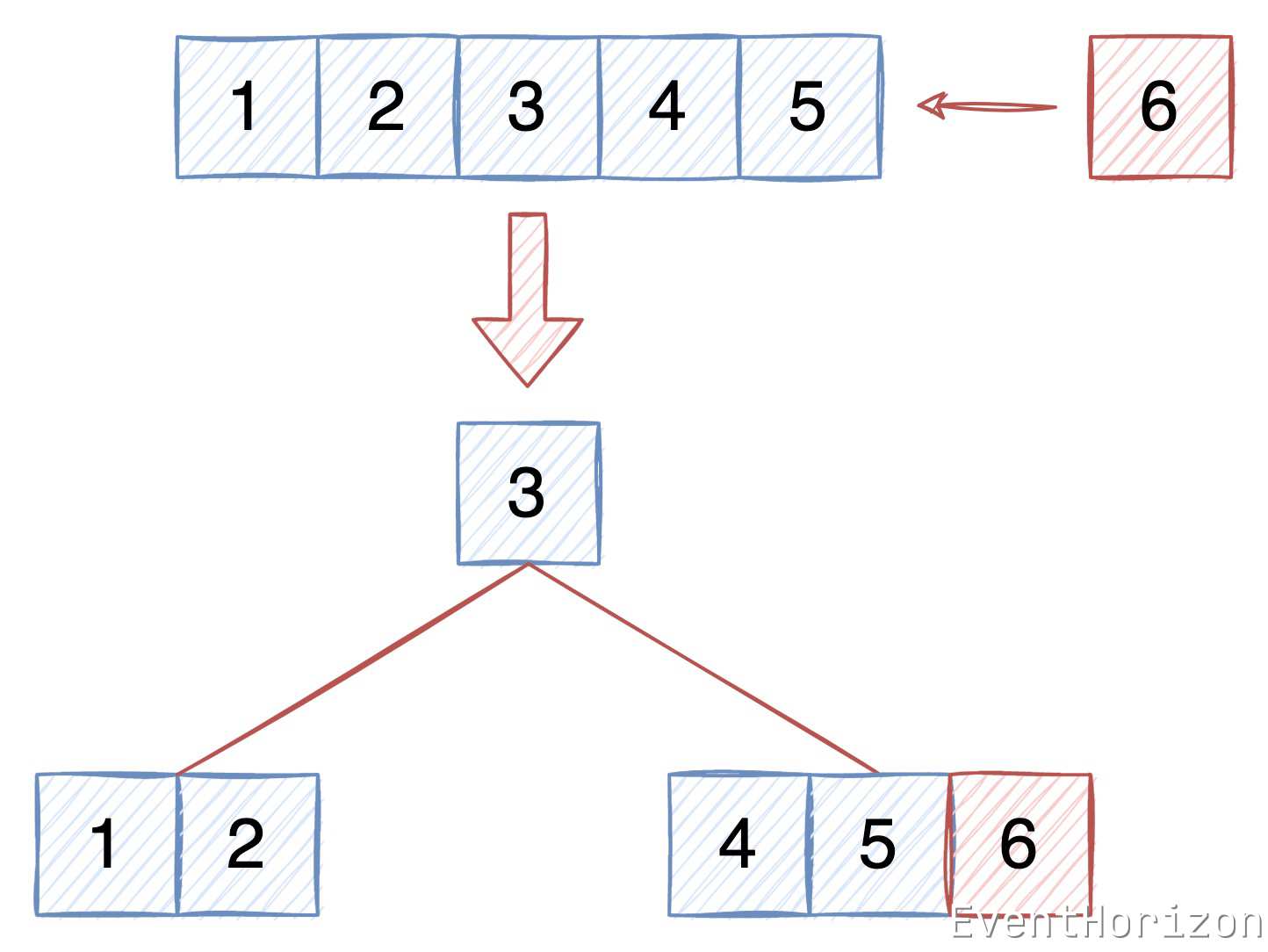
分裂分為以下幾個步驟（不一定要按這個順序）：

建立一個新的節點，作為新的根節點。
將原根節點作為新根節點的第一個子節點。
將原根節點中間（索引記為mid）的 Item 移動到新的根節點中，作為新根節點的第一個 Item。
建立一個新的節點。
將原根節點中間 Item 右邊的 Item（mid+1開始）移動到新節點中。
將原根節點中間 Item 右邊的子節點（mid+1開始）移動到新節點中。
將新節點作為新根節點的第二個子節點。

非根節點的分裂

假設當前節點是父節點的第 k 個子節點，也就是父節點 Items[k]（用PItems代指）的左子節點，或者說是PItems[k-1] 的右子節點。當前節點中所有 Item 的 Key 都在 (PItems[k-1], PItems[k])區間內。

分裂分為以下幾個步驟：

將中間（索引記為mid）的 Item （記作MItem）提升到父節點中，插入 PItems[k]，原來的 PItems[k] 移動至 PItems[k+1]，父節點中的 Item 依然保持有序。
建立新的節點。
將右半部分（mid+1開始）的 Item 移至新節點。
將右半部分（mid+1開始）的 子節點 移至新節點。
將新的節點插入父節點的子節點的第 k+1 個位置，也就是作為剛改過位置的 MItem 的右子節點，MItem 的 Key 小於其右子樹中所有 Item，順序性也不會遭到破壞。

新插入的 Item 會根據 Key 的大小，插入到分裂後的左節點或者右節點中。

下圖所示B樹 degree 為 3，每個 Node 最多有 5(2*3-1)個 Item，在[4,5,6,8,9]所在節點插入 7 需先進行分裂。6 將被提升到根節點中，原來的 6 所在節點將被分裂成兩個節點，7 會被插入到右側的新節點中。

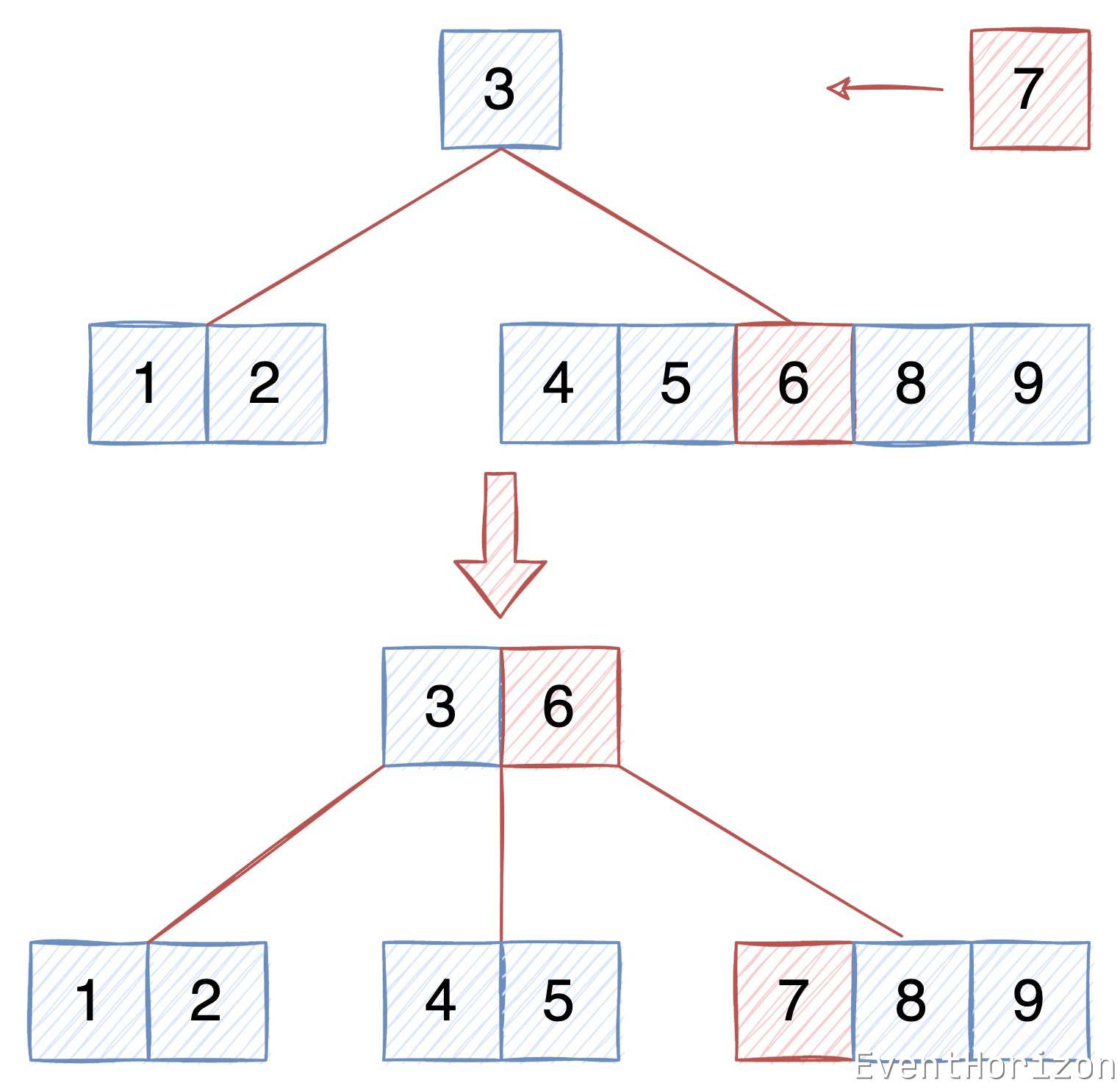
分裂導致樹的高度增加

節點在分裂的時候，如果父節點已經滿了，那麼父節點也需要分裂，這樣就會導致父節點的父節點也需要分裂，以此類推，直到根節點。

而根節點的分裂，會導致樹的高度增加。

新 Item 的插入是發生在葉子節點的，分裂也是從葉子節點開始。如果一個節點一開始是葉子節點，隨著資料的增加，它始終都是葉子節點，葉子節點分裂後，新的葉子節點也是同一高度的。

這其實解答了上文提到的問題：為什麼B樹的葉子節點都在同一層。

提前分裂

B樹中資料的插入過程，是一個從根節點不斷向下尋找合適葉子節點的過程。

而分裂是一個從葉子節點不斷向上的過程。

因此分裂演演算法的實際實現中，為了避免回溯性分裂（磁碟儲存中，回溯帶來的 overhead 很大），一般會在向下尋找的過程中提前去分裂已經滿了的節點。

插入演演算法實現

在插入新 Item 的過程中，BTree 本質上只是一個入口，大部分的邏輯都是和節點相關的，因此我們會把主要的邏輯定義在節點中。

Key 已存在時的處理策略

新插入的 Item 的 Key 可能已經存在了，針對已經存在的 Key 的處理方式，這邊參考 Dictionary 的處理方式：

通過 Indexer 插入資料時新 Value 覆蓋舊 Value。
通過 Add 插入資料時扔出異常。
通過 TryAdd 插入資料時不作任何處理。

對應列舉如下：

internal enum InsertionBehavior
{
    /// <summary>
    /// 預設操作，如果 key 已經存在，則不會更新 value
    /// </summary>
    None = 0,

    /// <summary>
    /// 如果 key 已經存在，則更新 value
    /// </summary>
    OverwriteExisting = 1,

    /// <summary>
    /// 如果 key 已經存在，則丟擲異常
    /// </summary>
    ThrowOnExisting = 2
}

並定義對應的處理結果列舉

internal enum InsertionResult
{
    None = 0,
    Added = 1,
    Updated = 2,
}

public sealed class BTree<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue?>>
{
    #region Indexers

    public TValue? this[[NotNull] TKey key]
    {
        get
        {
            if (TryGetValue(key, out var value))
            {
                return value;
            }

            throw new KeyNotFoundException();
        }
        set => TryInsert(key, value, InsertionBehavior.OverwriteExisting);
    }    

    #endregion

    #region Public Methods

    /// <summary>
    /// 往B樹中新增一個鍵值對
    /// </summary>
    /// <param name="key">要新增的元素的key</param>
    /// <param name="value">要新增的元素的value</param>
    /// <exception cref="ArgumentNullException">key是null</exception>
    /// <exception cref="ArgumentException">key已經存在</exception>
    public void Add([NotNull] TKey key, TValue? value) =>
        TryInsert(key, value, InsertionBehavior.ThrowOnExisting);

    /// <summary>
    /// 嘗試往B樹中新增一個鍵值對
    /// </summary>
    /// <param name="key">要新增的元素的key</param>
    /// <param name="value">要新增的元素的value</param>
    /// <returns>true:新增成功;false:新增失敗</returns>
    public bool TryAdd([NotNull] TKey key, TValue? value) =>
        TryInsert(key, value, InsertionBehavior.None);

    #endregion
}

插入演演算法

在 Node 中定義分裂和判斷是否要提前分裂的方法

internal class Node<TKey, TValue>
{
    /// <summary>
    /// 將當前<see cref="Node{TKey,TValue}"/>分裂成兩個<see cref="Node{TKey,TValue}"/>。
    /// </summary>
    /// <returns>中間位置的<see cref="Item{TKey,TValue}"/>和分裂後的第二個<see cref="Node{TKey,TValue}"/></returns>
    public (Item<TKey, TValue?> MiddleItem, Node<TKey, TValue?> SecnodNode) Split()
    {
        int middleIndex = ItemsCount / 2;
        var middleItem = _items[middleIndex];
        var secondNode = new Node<TKey, TValue?>(_degree, _comparer);

        // 將中間位置後的所有Item移動到新的Node中
        for (int i = middleIndex + 1; i < ItemsCount; i++)
        {
            secondNode._items.Add(_items[i]);
        }

        _items.Truncate(middleIndex);

        if (!IsLeaf)
        {
            // 將中間位置後的所有子節點移動到新的Node中
            for (int i = middleIndex + 1; i < ChildrenCount; i++)
            {
                secondNode._children.Add(_children[i]);
            }

            _children.Truncate(middleIndex + 1);
        }

        return (middleItem, secondNode);
    }

    /// <summary>
    /// 如果指定的子節點已滿，則將其分裂為兩個子節點，並將中間的 <see cref="Item{TKey,TValue}"/>> 插入到當前節點中。
    /// </summary>
    /// <param name="childIndex">指定的子節點的索引</param>
    /// <returns>True 表示已經分裂了子節點，False 表示沒有分裂子節點</returns>
    private bool MaybeSplitChildren(int childIndex)
    {
        var childNode = _children[childIndex];
        if (childNode.IsItemsFull)
        {
            var (middleItem, secondNode) = childNode.Split();
            _items.InsertAt(childIndex, middleItem);
            // 將新node插入到當前node的children中
            _children.InsertAt(childIndex + 1, secondNode);
            return true;
        }

        return false;
    }
}

在 BTree 中定義插入方法

public sealed class BTree<TKey, TValue>
    private bool TryInsert([NotNull] TKey key, TValue? value, InsertionBehavior behavior)
    {
        ArgumentNullException.ThrowIfNull(key);

        if (_root == null)
        {
            _root = new Node<TKey, TValue?>(_degree, _comparer);
            _root.Add(new Item<TKey, TValue?>(key, value));
            _count++;
            return true;
        }

        if (_root.IsItemsFull)
        {
            // 根節點已滿，需要分裂
            var (middleItem, secondNode) = _root.Split();
            var oldRoot = _root;
            _root = new Node<TKey, TValue?>(_degree, _comparer);
            // 將原來根節點中間的元素新增到新的根節點
            _root.Add(middleItem);
            // 將原來根節點分裂出來的節點新增到新的根節點
            _root.AddChild(oldRoot);
            _root.AddChild(secondNode);
        }

        // 從根節點開始插入，如果插入的 Key 已經存在，會按照 behavior 的值進行處理
        var insertionResult = _root.TryInsert(key, value, behavior);
        if (insertionResult == InsertionResult.Added) _count++;

        return insertionResult != InsertionResult.None;
    }
}

在 Node 中定義插入方法，遞迴呼叫直至找到葉子節點，然後在葉子節點中插入

internal class Node<TKey, TValue>
{
    public InsertionResult TryInsert(TKey key, TValue? value, InsertionBehavior behavior)
    {
        // 如果當前key已經存在, 根據插入行為決定是否替換
        if (_items.TryFindKey(key, out int index))
        {
            switch (behavior)
            {
                case InsertionBehavior.OverwriteExisting:
                    _items[index].Value = value;
                    return InsertionResult.Updated;
                case InsertionBehavior.ThrowOnExisting:
                    throw new ArgumentException($"An item with the same key has already been added. Key: {key}");
                default:
                    return InsertionResult.None;
            }
        }

        // 如果當前節點是葉子節點，則直接插入
        if (IsLeaf)
        {
            // index 是新的 item 應該插入的位置，items 按順序排列
            _items.InsertAt(index, new Item<TKey, TValue?>(key, value));
            return InsertionResult.Added;
        }

        // 如果當前節點的子節點已經滿了，則需要分裂
        // 如果當前節點的子節點沒有滿，則不需要分裂
        // 如果當前節點的子節點分裂了，則需要判斷當前key是否大於分裂後的中間key
        // 如果當前key大於分裂後的中間key，則需要向右邊的子節點插入
        // 如果當前key小於分裂後的中間key，則需要向左邊的子節點插入

        // index 是新的 item 應該插入的位置，如果當做children的索引，則代表應該插入的位置的右邊的子節點
        if (MaybeSplitChildren(index))
        {
            // rightmostItem 是子節點分裂後的中間的 item，被提升到當前節點的 items 中的最後一個位置了
            var middleItemOfChild = _items[index];

            switch (_comparer.Compare(key, middleItemOfChild.Key))
            {
                case > 0:
                    // 如果當前key大於分裂後的中間key，則需要向右邊的子節點插入
                    index++;
                    break;
                case < 0:
                    // 如果當前key小於分裂後的中間key，則需要向左邊的子節點插入
                    break;
                default:
                    // 如果當前key等於分裂後的中間key，根據插入行為決定是否替換
                    switch (behavior)
                    {
                        case InsertionBehavior.OverwriteExisting:
                            middleItemOfChild.Value = value;
                            return InsertionResult.Updated;
                        case InsertionBehavior.ThrowOnExisting:
                            throw new ArgumentException(
                                $"An item with the same key has already been added. Key: {key}");
                        default:
                            return InsertionResult.None;
                    }
            }
        }

        // 往子節點插入
        return _children[index].TryInsert(key, value, behavior);
    }
}

總結

B樹中的資料是按照順序儲存的，所以可以使用二分查詢法來查詢資料，時間複雜度為 O(log n)。

往B樹插入資料的過程是一個尋找合適的葉子節點的過程，然後在葉子節點中插入資料，時間複雜度為 O(log n)。

B樹的節點中儲存的資料量是有限的，所以在插入資料時，可能會發生節點分裂，這樣就會導致樹的高度增加，所以在插入資料時，需要判斷是否需要分裂，如果需要分裂，就需要將中間的資料提升到父節點中，以此類推，直到根節點，如果根節點也需要分裂，就需要新建一個根節點，然後將原來的根節點和分裂出來的節點作為新的根節點的子節點。

參考資料

PingCAP 寶寶床邊故事集：儲存引擎

B樹、B+樹索引演演算法原理（上）

B樹維基百科

Google 用 Go 實現的記憶體版 B樹

渴望力量系列《演演算法導論第三版》

歡迎關注個人微信公眾號 EventHorizonCLI ，最新的原創技術文章將在優先這裡釋出。

圖解B樹及C#實現（1）

前言