【影象處理筆記】傅立葉變換
0 引言
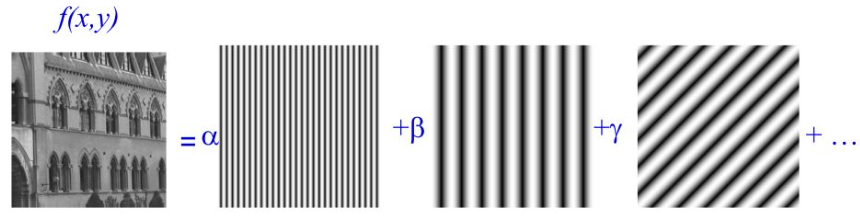
在之前的部落格影象增強,傅立葉變換(OpenCV)中都有用到過傅立葉變換,但一直都不是特別理解,現系統地學習一下。先來看一個視訊傅立葉級數與傅立葉變換,我們瞭解到任何周期函數都可以表示為不同頻率的正弦函數和/或餘弦函數之和,其中每個正弦函數和/或餘弦函數都乘以不同的係數。如何找到是哪些頻率組成的該周期函數?可以看一下這篇文章從傅立葉變換進階到小波變換。學習傅立葉還是要踏踏實實弄清楚公式和概念,沒有捷徑,接下來我們來推導公式。
1 傅立葉級數
週期為T的連續變數t的周期函數f(t),可表示為乘以適當係數的正弦函數和餘弦函數之和。這個和就是傅立葉級數,其形式為
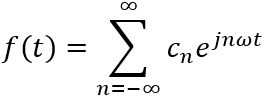
式中,Cn是傅立葉級數
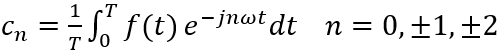
從上式可知,若要將一個週期訊號展開為傅立葉級數形式,實際上就是確定級數,接下來我們討論如何求出cn。
1.1 三角函數正交性
三角函數是周期函數,其在-π到π的積分必定為0,即
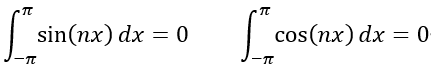
由三角函數的積化和差公式,可以繼續推匯出下列公式
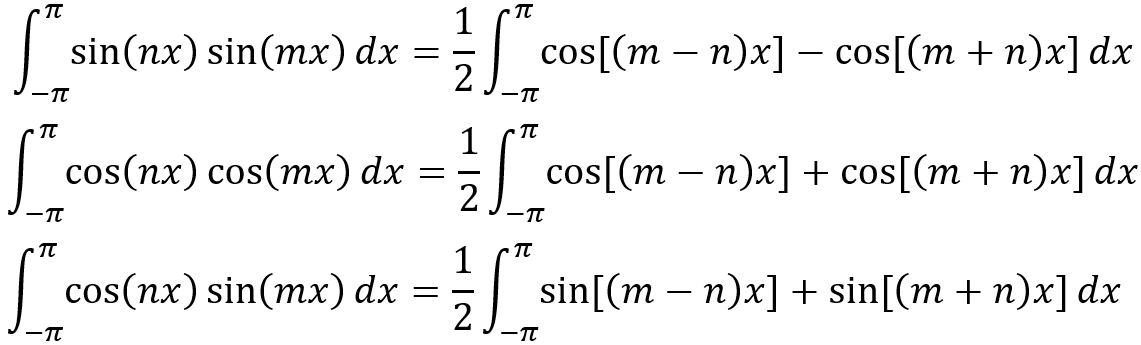
因為三角函數在-π到π內的積分為0,因此當m≠n時上面三個式子必定為0,因此可以得出以下結論,頻率不同的三角函數相乘在一個週期內(-π到π)的積分必定為0。
假設一函數f(t)由一個直流分量和若干正餘弦函陣列成
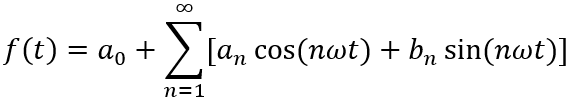
在上式兩邊同時乘以sin(kωt),並對它們在一個週期內進行積分,可得
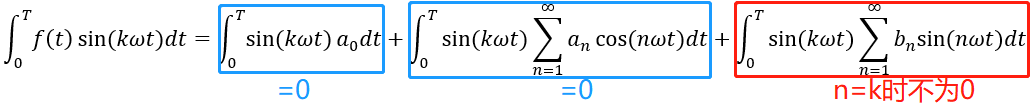
化簡得
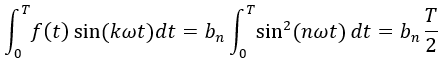
因此,可得bn,同理也可得an

1.2 尤拉公式與傅立葉級數
根據尤拉公式
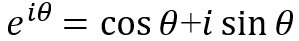
當θ=nωt和θ=-nωt時,

將這兩項代入傅立葉級數
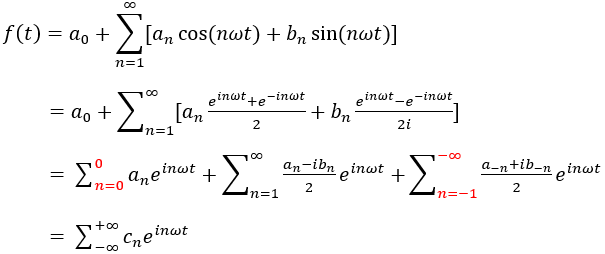
當n=0時,代入上一小節得到的a0
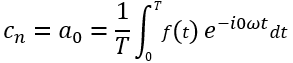 當n=1,2,3,...時,代入an,bn
當n=1,2,3,...時,代入an,bn
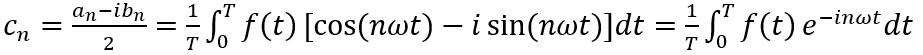
當n=-1,-2,-3,...時,代入an,bn
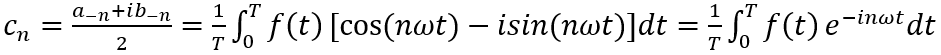
可以看出,對於任意的n,所有Cn的表示式都是一樣的,傅立葉級數最終可以寫為:

得證。
2 傅立葉變換
2.1 一維傅立葉變換
傅立葉級數是針對周期函數的,而傅立葉變換針對非周期函數,一個非周期函數可以看做週期無限大的函數。當T趨於無窮大時,頻率間隔ω=2π/T趨於無窮小;Δω=(n+1)ω-nω=ω=2π/T,因此Δω也趨於0,1/T=Δω/2π;ΣΔω可以寫成積分的形式∫dω。我們以nω為變數,當ω不等於0時,nω為離散值,,但當ω趨於無窮小時,nω就變成連續的量,令nω=W。
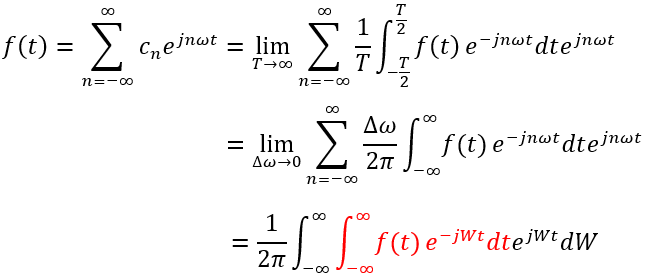
我們將這個式子中標紅的部分稱作函數f(t)的傅立葉變換,記作F(w),即
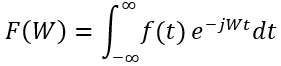
而原始函數f(t)可以寫為
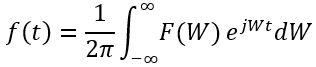
我們稱之為傅立葉反變換。
2.2 二維傅立葉變換
二維連續函數f(x,y)的傅立葉正變換為
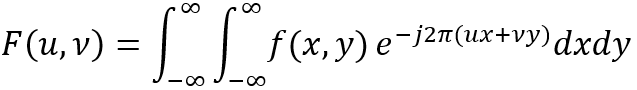
相應的傅立葉逆變換公式為
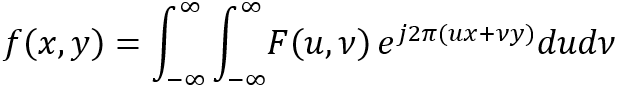 但是在計算機領域,計算機一般處理的是數位訊號,只能進行有限次計算,因此將這種受限下的傅立葉變換成為離散傅立葉變換(Discrete Fourier Transform,DFT)。二維離散函數f(x,y)的傅立葉正變換的公式如下:
但是在計算機領域,計算機一般處理的是數位訊號,只能進行有限次計算,因此將這種受限下的傅立葉變換成為離散傅立葉變換(Discrete Fourier Transform,DFT)。二維離散函數f(x,y)的傅立葉正變換的公式如下:
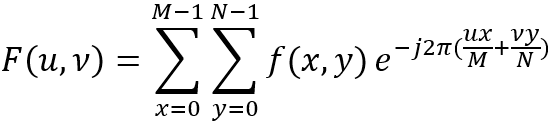 其中,u=0,1,2,...,M-1;v=0,1,2,...N-1。
其中,u=0,1,2,...,M-1;v=0,1,2,...N-1。
相應的傅立葉逆變換的公式如下:
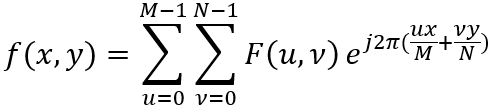
其中,x=0,1,2,...,M-1;y=0,1,2,...N-1。
一維訊號是一個序列,傅立葉變換將其分解成若干個一維的簡單函數之和。二維訊號可以說是一個影象,二維傅立葉變換將影象分解成若干個複平面波之和。通過上面的公式,我們可以計算出,每個平面波在影象重的成分是多少。從公式也可以看出,二維傅立葉變換就是將影象與每個不同頻率的不同方向的複平面波做內積(先再求和),也就是一個求在基上投影的過程。一維的正弦波可以通過三個引數確定,頻率ω,幅度A和相位φ。因此在頻域中,一維座標表示頻率,每個座標對應的函數值F(ω)是一個複數,它的模|F(w)|就是幅度A,幅角∠F(w)就是相位。而二維正弦平面波需要四個引數,其中三個和一維一樣(頻率ω,幅度A和相位φ),令一個是方向n。如下圖所示,兩個平面波僅在方向引數上不同:
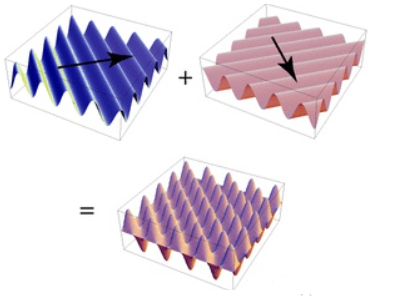
如何儲存頻率ω,幅度A,相位φ和方向n這些引數呢?和一維一樣,幅度和相位可以用一個複數表示,複數的模是幅度,幅角是相位。向量有方向和長度,可以用來表示方向和頻率。一個向量n=(u,v),向量的模√u2+v2代表這個平面波的頻率,方向是平面波的方向,在該點的值F(u,v)表示幅度和相位。包含所有(u,v)點的矩陣是K空間,如下圖所示
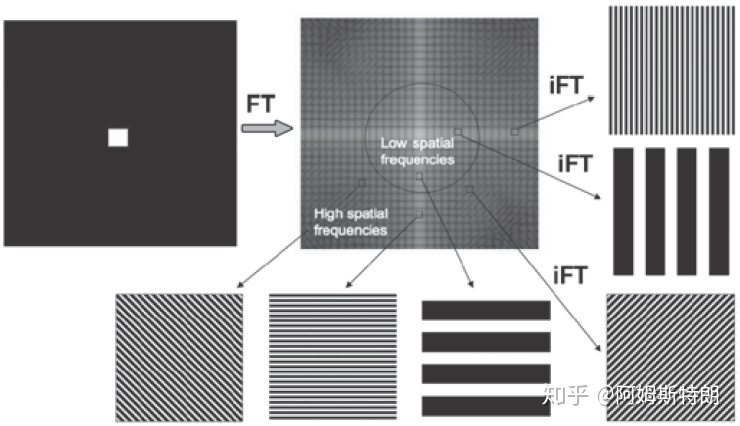
上圖中,頻譜圖的中心為原點,即u=0,v=0,中間區域為低頻,頻率低週期大,條紋間隔寬,從中間向外,頻率增大,平面波週期減小,條紋間隔小。影象區域灰度越高表示該頻率平面波在影象中成分越多,由於低頻表示影象灰度平穩區域,高頻表示細節和邊緣,所以影象主要是低頻,頻譜圖中間灰度較高。在不同象限的點所代表的平面波方向不同。連結中有很多影象的二維傅立葉變換頻譜圖,可以驗證下自己弄懂了沒。
3 應用
二維離散傅立葉變換(Two-Dimensional Discrete Fourier Transform)是一種數位變換方法,一般應用於將影象從空間域轉至頻域,在影象增強、影象去噪、影象邊緣檢測、影象特徵提取、影象壓縮等等應用中都起著極其重要的作用。
3.1 頻域濾波
影象實質上是二維矩陣。將空間域(二維灰度數表)的影象轉換到頻域(頻率數表)能夠更直觀地觀察和處理影象,也更有利於進行頻域濾波等操作。在部落格影象增強中介紹了不少常用的低通濾波器,也在部落格傅立葉變換中介紹過OpenCV中傅立葉變換的寫法。接下來的這個範例和之前的寫法有些不同。
範例 頻域濾波
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main() {
clock_t start = clock();
Mat src = imread("E:/C++projects/CH11/CH11/5.png", 0);
imshow("src", src);
// 填充到傅立葉變換最佳尺寸 (gpu下加速明顯)
int h = getOptimalDFTSize(src.rows);
int w = getOptimalDFTSize(src.cols);
Mat padded;
copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));
Mat pMat = Mat(padded.size(), CV_32FC1);
// 中心化 (在時域做中心化,傅立葉變換後的頻譜圖低頻在中心)
for (int i = 0; i < padded.rows; i++)
{
for (int j = 0; j < padded.cols; j++)
{
pMat.at<float>(i, j) = pow(-1, i + j) * padded.at<uchar>(i, j);
}
}
// 傅立葉變換
Mat planes[] = { pMat, Mat::zeros(padded.size(), CV_32F) };
Mat complexImg;
merge(planes, 2, complexImg);
dft(complexImg, complexImg, DFT_COMPLEX_OUTPUT);
// 顯示頻譜圖
split(complexImg, planes);
Mat magMat;
magnitude(planes[0], planes[1], magMat);
magMat += 1;
log(magMat, magMat);
normalize(magMat, magMat, 0, 255, NORM_MINMAX);
magMat.convertTo(magMat, CV_8UC1);
// 低通濾波
//Mat mask(Size(w, h), CV_32FC2, Scalar(0, 0));
//circle(mask, Point(w / 2, h / 2), 50, Scalar(255, 255), -1);
//complexImg = complexImg.mul(mask);
//高通濾波
Mat mask(Size(w, h), CV_32FC2, Scalar(255, 255));
circle(mask, Point(w / 2, h / 2), 50, Scalar(0, 0), -1);
complexImg = complexImg.mul(mask);
// 傅立葉反變換
Mat dst, tmp;
idft(complexImg, tmp, DFT_REAL_OUTPUT);
// 去中心化
for (int i = 0; i < padded.rows; i++)
{
for (int j = 0; j < padded.cols; j++)
{
pMat.at<float>(i, j) = pow(-1, i + j) * tmp.at<float>(i, j);
}
}
dst = pMat({ 0,0,src.cols ,src.rows }).clone();
normalize(dst, dst, 0, 1, NORM_MINMAX);
dst.convertTo(dst, CV_8U, 255);
imshow("dst", dst);
clock_t end = clock();
cout << "spend time:" << end - start << "ms" << endl;
waitKey(0);
return 0;
}

不知道有沒有人發現,是中心化的方法不一樣。之前是在頻域做的中心化,這次是在時域做中心化→傅立葉變換→濾波→傅立葉逆變換→去中心化。這是傅立葉變換的平移性質,在第4節會詳細講解下。
3.2 加速濾波計算
用大小為m×n元素的核對大小為M×N的影象進行濾波時,需要的運算次數為MNmn(乘法和加法)。如果核是可分離的,那麼運算次數可減少為MN(m+n)。在頻率域中執行等效濾波所需要的運算次數僅為2MNlog2MN,前面的係數2表示我們要計算一次正FFT和一次反FFT。
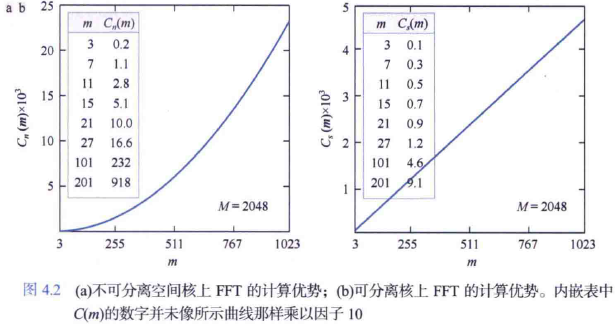
為說明頻率域濾波相對於空間濾波的計算優勢,我們分別考慮大小為M×M的方形影象與m×m的核。採用不可分離的核所需的運算次數為M2m2,採用可分離的核所需的運算次數為2M2m,而採用FFT對這種影象濾波所需的運算次數為2M2log2M2,定義FFT方法的計算優勢為

兩種情況下,當C(m)>1時,FFT方法的計算優勢更大(根據計算次數);而當C(m)≤1時,空間濾波的優勢更大。下圖顯示了中等大小影象(M=2048)的Cn(m)與m的曲線關係。對於7×7或更大的核,FFT具有計算優勢。這一優勢隨著m的增大而迅速增大,例如m=101時計算優勢超過200,而m=201時計算優勢接近1000.下面說明這一優勢的含義。如果用FFT對大小為2048×2048的一組影象進行濾波需要1分鐘,那麼用大小為201×201元素的不可分離核對同一組影象濾波要17小時。這一差異非常明顯,因此清楚地表明瞭使用FFT進行頻率域處理的重要性。
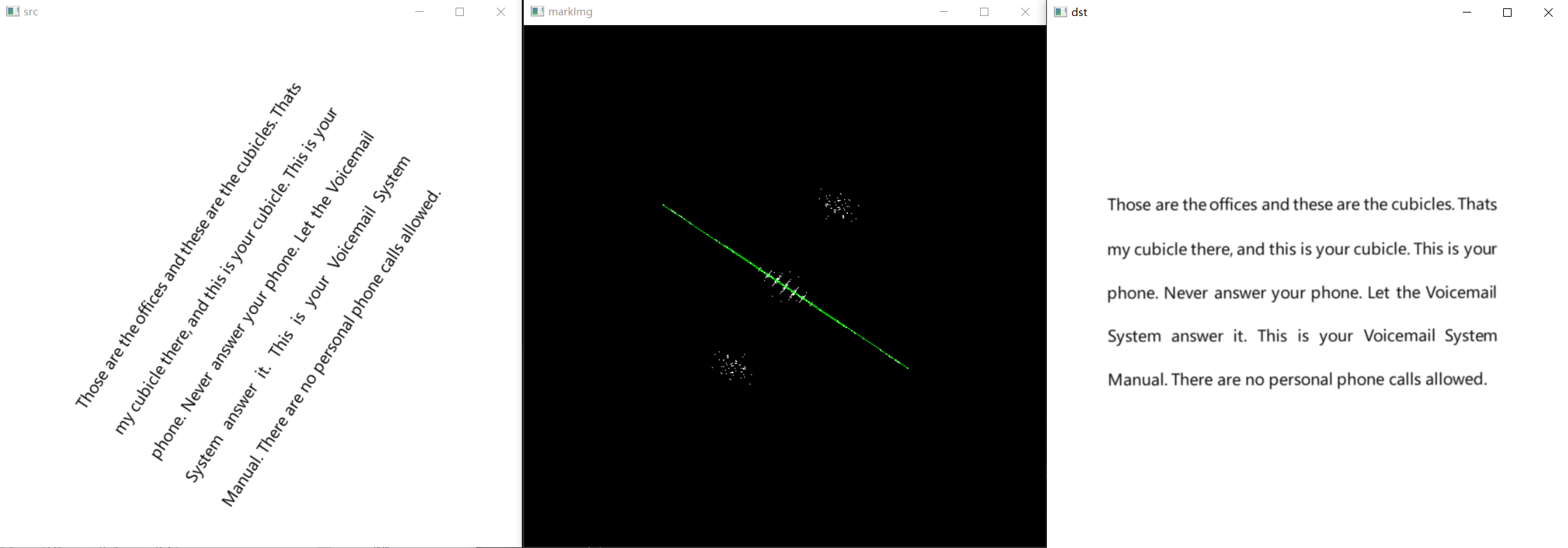
3.3 傾斜文字校正
對於分行的文字,其頻率譜上一定會有一定的特徵,當影象旋轉時,其頻譜也會同步旋轉,因此找出這個特徵的傾角,就可以將影象旋轉校正回去。這是二維傅立葉變換的旋轉性質,傅立葉變換對

使用極座標
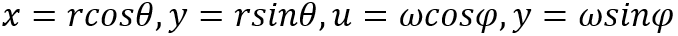
可得到如下變換對
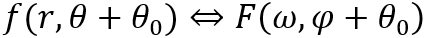
它指出,若f(x,y)旋轉θ0角度,則F(u,v)也旋轉相同的角度。反之,若F(u,v)旋轉某個角度,f(x,y)也旋轉相同的角度。
範例 傾斜文字校正
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
double point2Line(Point2f pointP, Point2f pointA, Point2f pointB)
{
//求直線方程
double A = 0, B = 0, C = 0;
A = pointA.y - pointB.y;
B = pointB.x - pointA.x;
C = pointA.x * pointB.y - pointA.y * pointB.x;
//代入點到直線距離公式
double distance = 0;
double tmp1 = abs(A * pointP.x + B * pointP.y + C);
double tmp2 = ((float)sqrtf(A * A + B * B));
distance = tmp1 / tmp2;
return distance;
}
int main() {
vector<string> filenames;
glob("./", filenames);
for (int n = 0; n < filenames.size(); n++) {
string filename = filenames[n];
Mat src = imread(filename, 0);
// 填充到傅立葉變換的最佳尺寸
int h = getOptimalDFTSize(src.rows);
int w = getOptimalDFTSize(src.cols);
Mat padded;
copyMakeBorder(src, padded, 0, h - src.rows, 0, w - src.cols, BORDER_CONSTANT, Scalar::all(0));
// 傅立葉變換
Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) };
Mat complexImg;
merge(planes, 2, complexImg);
dft(complexImg, complexImg, DFT_COMPLEX_INPUT | DFT_COMPLEX_OUTPUT);
// 求幅值
split(complexImg, planes);
Mat magMat;
magnitude(planes[0], planes[1], magMat);
magMat += 1;
log(magMat, magMat);
normalize(magMat, magMat, 0, 255, NORM_MINMAX);
magMat.convertTo(magMat, CV_8UC1);
// 把零頻移到中心
Mat magImg = magMat.clone();
int cx = magImg.cols / 2;
int cy = magImg.rows / 2;
Mat q1 = magImg({ 0, 0, cx, cy });
Mat q2 = magImg({ 0, cy, cx, cy });
Mat q3 = magImg({ cx, 0, cx, cy });
Mat q4 = magImg({ cx, cy, cx, cy });
Mat temp;
q1.copyTo(temp);
q4.copyTo(q1);
temp.copyTo(q4);
q2.copyTo(temp);
q3.copyTo(q2);
temp.copyTo(q3);
// 霍夫直線檢測有角度的斜線
Mat binImg;
threshold(magImg, binImg, 150, 255, THRESH_BINARY);
Mat markImg;
cvtColor(binImg, markImg, COLOR_GRAY2BGR);
vector<Vec4i> lines;
Vec4i l;
HoughLinesP(binImg, lines, 1, CV_PI / 180.0, 30, 200, 50);
Point2f p = Point2f(magImg.cols / 2.0, magImg.rows / 2.0);
for (int i = 0; i < lines.size(); i++)
{
if (abs(lines[i][1] - lines[i][3]) > 15) {
line(markImg, Point(lines[i][0], lines[i][1]), Point(lines[i][2], lines[i][3]), Scalar(0, 255, 0), 1, 8, 0);
l = lines[i];
}
}
float theta = atan((l[1] - l[3]) * 1.0 / (l[0] - l[2]) * src.cols / src.rows) * 180 / CV_PI;
float angle = theta <= 0 ? theta + 90 : theta - 90;
// 放射變換
Point2f center = Point2f(src.cols / 2.0, src.rows / 2.0);
Mat rotMat = getRotationMatrix2D(center, angle, 1.0);
Mat dst = Mat::ones(src.size(), CV_8UC1);
warpAffine(src, dst, rotMat, src.size(), 1, 0, Scalar(255, 255, 255));
imshow("src", src);
imshow("markImg", markImg);
imshow("dst", dst);
waitKey(0);
}
return 0;
}
4 Q&A
Q: 為什麼要中心化?如何中心化?
直接對數位影像進行二維DFT變換得到的頻譜圖是高頻在中間,低頻在四角。為了把能量(在低頻)集中起來便於使用濾波器,可以利用二維DFT的平移性質對頻譜進行中心化。頻譜圖比較亮的地方是低頻,影象的能量一般都是集中在低頻部分。中心化不是必須的,主要是為了方便理解和濾波。

根據二維傅立葉的平移性質,用<=>表示函數和其傅立葉變換的對應性
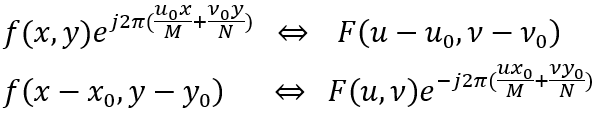
第一個公式表明,將f(x,y)與一個指數項相乘就相當於把其變換後的頻域中心移動到新的位置。第二個公式表明將F(u,v)與一個指數項相乘就相當於把其變換後的空域中心移到新的位置,同時可以看出對f(x,y)的平移不會影響其傅立葉變換的幅值。將u0=M/2和v0=N/2代入第一個公式,指數部分就變為
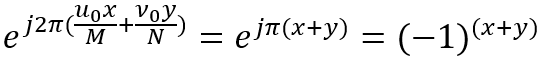
代入上面的公式
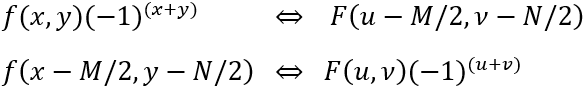
也就是說,對數位影像的每個畫素點的取值直接乘以(-1)^(x+y),x和y是畫素座標。這之後再做傅立葉變換,最後即為中心化後的傅立葉變換。和在頻域移動M/2和N/2一樣的效果。
Q: 為什麼用影象二維傅立葉變換的相位譜進行反變換,能夠大致得到原圖的形狀,而幅度譜則不行呢?
k空間中儲存的是一個複數,其幅度代表平面波的波動的大小,相位代表平面波的相位也就是偏離原點的多少。從k空間回覆影象的時候,是將每個複平面乘上對應的復係數,相加而成。可以分為兩步:(1)乘上波動大小(幅度)(2)移動相應的距離(相位)
範例 譜和相角對影象資訊的貢獻
只用相角重建男孩影象,就是令|F(u,v)|=1,可以看出,影象丟失了灰度資訊,但有形狀特徵。只使用譜重建,這意味著指數項為1,也就是令相角為0,此時結果中值包含灰度資訊,沒有形狀資訊。最後兩張圖顯示了相位在確定影象空間特徵內容方面的優勢。
...
Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) };
Mat complexImg;
merge(planes, 2, complexImg);
dft(complexImg, complexImg, DFT_COMPLEX_OUTPUT);
split(complexImg, planes);
Mat magMat;
magnitude(planes[0], planes[1], magMat);
// 相角重建
//divide(planes[0], magMat, planes[0]);
//divide(planes[1], magMat, planes[1]);
//譜重建
planes[0] = magMat;
planes[1] = Mat::zeros(padded.size(), CV_32F);
merge(planes, 2, complexImg);
Mat dst, tmp;
idft(complexImg, tmp, DFT_REAL_OUTPUT);
...

Q: 傅立葉變換為什麼要填充0?
A: (1)提升運算效能;(2)時域補零相當於頻域插值,補零操作增加了頻域的插值點數,讓頻域曲線看起來更加光滑,也就是增加了FFT頻率解析度。從傅立葉變換公式可以看出,頻域的點數和時域的點數是一樣的,時域補零後,取樣點增加。詳見快速傅立葉變換(FFT)中為什麼要「補零」?
Q: 什麼是頻率(譜)洩漏?
頻率洩漏是指傅立葉變換後的頻譜中出現了本不該有的頻率分量。原來的訊號的序列我們認為是無限長的,但我們要分析某個訊號的頻譜的時候只能對它有限長度的序列進行分析,相當於時域上對它進行了加窗,類似於盒式函數乘上f(t),在頻率域中這一相乘意味著原變換與一個sinc函數的折積,進而導致由sinc函數的高頻分量產生所謂的頻率洩漏。歸根結底,頻率洩漏的原因就是加窗導致的序列長度有限。
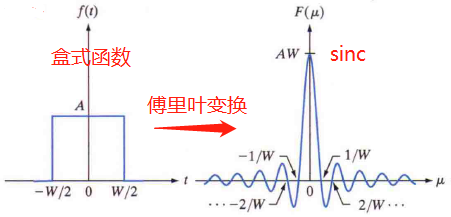
頻率洩漏會使得影象塊效應。雖然頻率洩漏無法完全消除,但讓取樣後的函數乘以另一個兩端平滑地過渡到0的函數,可明顯降低頻率洩漏。這個想法是為了抑制「盒式函數」的急劇過渡。
參考
1. 岡薩雷斯《數位影像處理(第四版)》Chapter4(所有圖片可在連結中下載)
2. 傅立葉變換推導詳解
3. 傅立葉級數與傅立葉變換
5. 形象理解二維傅立葉變換