論文資訊

論文標題：Probabilistic Contrastive Learning for Domain Adaptation
論文作者：Junjie Li, Yixin Zhang, Zilei Wang, Keyu Tu
論文來源：aRxiv 2022
論文地址：download
論文程式碼：download

1 Abstract

　　標準的對比學習用於提取特徵，然而對於 Domain Adaptation 任務，表現不佳，主要原因是在優化過程中沒有涉及類權值優化，這不能保證所產生的特徵都圍繞著從源資料中學習到的類權值。為解決這一問題，本文中提出一種簡單而強大的概率對比學習（PCL），它不僅產生緊湊的特徵，而且還使它們分佈在類權值周圍。

2 Introduction

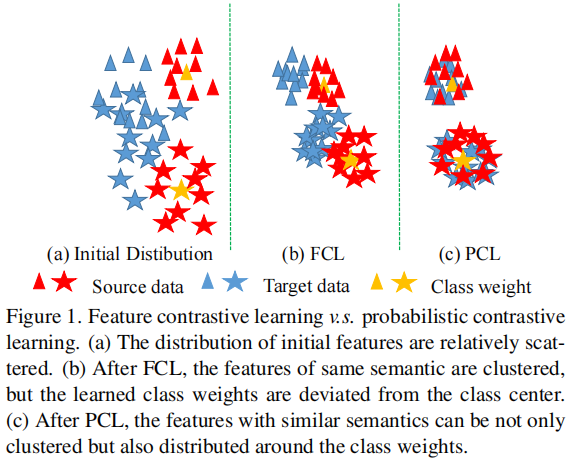
　　對於分類任務，需要確保特徵本身的可區分性，才能獲得良好的效能，即：具有相同語意的特性應該儘可能緊湊。然而，在 Domain Adaptation 中，由於目標域缺乏地面真實標籤，目標域上學習到的特徵通常是分散和難以區分的，如 Figure 1(a) 所示。但是對比學習可以在未標記資料上學習語意上緊湊的特徵表示，這傾向於將語意上相似的特徵聚在一起。因此，可在目標域上進行特徵對比學習（FCL），使目標域的特徵更容易區分，如 Figure 1(b) 所示。然而，本文發現 FCL 在 Domain Adaptation 方面帶來的改善非常有限（64.3%→64.5%）（見 Figure 2）。這一實證結果自然提出了一個問題：為什麼特徵對比學習在域自適應方向表現差？

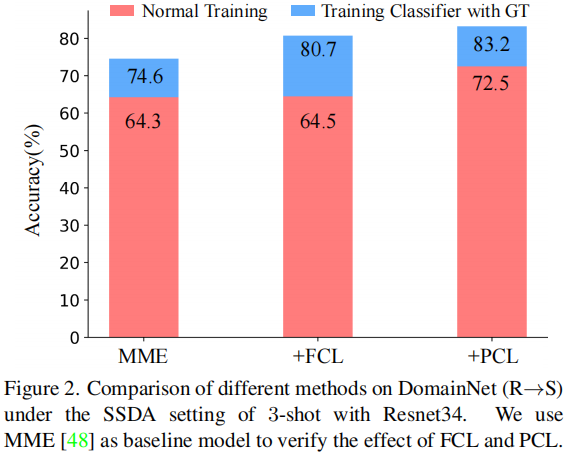
　　首先，驗證對比學習是否確實提高目標域特徵的可區分性。具體地說，先凍結特徵提取器，並使用地面真實標籤來訓練分類器。如 Figure 2 所示，在這種設定下，FCL 的準確率提高了6.1%（74.6%→80.7%），但實際的準確率僅提高了 0.2%（64.3%→64.5%）。實驗結果表明，FCL 確實可以提高特徵的可區分性。此外，在分類的學習過程中可能存在一些問題，導致將對比學習直接應用於領域自適應的表現不佳。

　　事實上，對於分類任務，類權值（全連線層的權值）需要接近特徵的類中心，而且特徵本身是足夠可區分的。也就是說，特徵需要接近其對應的類權重。目前的對比學習方法通常使用分類器之前的特徵來計算對比損失，其中在優化過程中不涉及類權值的資訊。因此，FCL 不能強制特性圍繞類權重。而在 Domain Adaptation 中，源域上有監督訊號，而源資料和目標資料通常來自不同的分佈。因此，學習到的類權值會偏離目標資料，因為它們只通過來自源域的監督訊號進行優化。雖然由於 FCL 的引入，目標特徵可以區分，但類權重很難有效地區分它們，如 Figure 1(b) 所示。因此，一個關鍵問題是如何將類資訊帶到優化過程中，以便強制將特性定位在相應的類權重周圍。

　　因此，提出了一個很自然的問題：只要引入類權重資訊，是否有可能具有接近類權重的特徵？為了引入類權重資訊，一個簡單的思想是直接使用分類器後的特徵來計算對比損失。然而，我們發現該方法並不能有效地提高 FCL 的效能，這說明簡單地引入類權值並不能有效地減少特徵與類權值之間的距離。因此，需要仔細設計一個對比學習損失，可以明確地縮小特徵和類權重之間的距離。

　　為深入理解這個問題，首先考慮了什麼樣的資訊可以表明該特性接近於它的類權重。為方便起見，定義了一組類權值 $W=\left(\mathbf{w}_{1}, \ldots, \mathbf{w}_{C}\right)$，一個特徵向量 $\mathbf{f}_{i}$ ，分類概率 $\mathbf{p}_{i}$，$C$ 是類別的數量，概率 $p_{i}$ 的第 $c$ 分量 $p_{i, c}$，由 $p_{i, c}=\frac{\exp \left(\mathbf{w}_{c}^{\top} \mathbf{f}_{i}\right)}{\sum_{j \neq c} \exp \left(\mathbf{w}_{j}^{\top} \mathbf{f}_{i}\right)+\exp \left(\mathbf{w}_{c}^{\top} \mathbf{f}_{i}\right)}$ 定義。假設 $\mathbf{f}_{i}$ 接近 $\mathbf{w}_{c}$，這意味著 $\mathbf{w}_{c}^{\top} \mathbf{f}_{i}$ 變大，$p_{i, c}$ 將接近 $1$。同時，當 $p_{i, c}$ 接近於 1 時， $\left\{p_{i, j}\right\}_{j \neq c}$ 將接近於 0，因為 $\sum_{j} p_{i, j}=1$。也就是說，當 $f_i$ 接近一個類權重時，概率 $p_i$ 將近似 one-hot 形式。

　　受這種直覺的啟發，我們鼓勵特徵的概率儘可能接近一個 one-hot 形式，以減少特徵和類權重之間的距離。在本工作中，我們發現，只要特徵被概率取代，並且去除 L2 歸一化，對比損失將自動迫使特徵的概率接近單熱形式，Figure 1(c) 說明了這些結果。

3 Method

　　我們用特徵提取器 $E$ 和分類器 $F$ 定義模型 $M=F \circ E$。這裡 $F$ 有引數 $W=\left(\mathbf{w}_{1}, \ldots, \mathbf{w}_{C}\right)$，其中 $C$ 是類的數量，$\mathbf{w}_{k}$ 是第 $k$ 個類的類權重（也稱為類原型）。

3.1 Feature Contrastive Learning

　　源域影象已有清晰的監督訊號，不再需要對比學習。因此，只計算目標域資料的對比學習損失。具體來說，設 $\mathcal{B}=\left\{\left(x_{i}, \tilde{x}_{i}\right)\right\}_{i=1}^{N}$ 是從目標域取樣得的批資料，其中 $N$ 是批大小，$x_{i}$ 和 $\tilde{x}_{i}$ 是一個樣本的兩個隨機變換。然後，我們使用 $E$ 來提取特徵，並得到 $\mathcal{F}=\left\{\left(\mathbf{f}_{i}, \tilde{\mathbf{f}}_{i}\right)\right\}_{i=1}^{N}$。特徵 $\mathbf{f}_{i}$ 和 $\tilde{\mathbf{f}}_{i}$ 是正樣本對，其他樣本是負樣本對。InfoNCE 損失如下：

　　　　$\ell_{\mathbf{f}_{i}}=-\log \frac{\exp \left(s g\left(\mathbf{f}_{i}\right)^{\top} g\left(\tilde{\mathbf{f}}_{i}\right)\right)}{\sum_{j \neq i} \exp \left(\operatorname{sg}\left(\mathbf{f}_{i}\right)^{\top} g\left(\mathbf{f}_{j}\right)\right)+\sum_{k} \exp \left(s g\left(\mathbf{f}_{i}\right)^{\top} g\left(\tilde{\mathbf{f}}_{k}\right)\right)} \quad\quad\quad(1)$

　　其中，$g(\mathbf{f})=\frac{\mathbf{f}}{\|\mathbf{f}\|_{2}}$ 是標準的 L2 標準化，$s $ 是溫度可調參。

3.2 Naive Solution

　　為引入類權重的資訊，最直接的方法是利用分類器後的特徵來計算對比損失，【即後文的 LCL】。4.1 節顯示 LCL 不能提高 FCL 的效能，這是因為然 LCL 引入了類權值的資訊，但 LCL 損失的優化過程並沒有直接限制特徵和類權值之間的距離。

　　交叉熵損失函數回顧：

　　　　$\operatorname{loss}(\mathrm{x}, \text { class })=-\log \left(\frac{\exp (\mathrm{x}[\text { class }])}{\sum_{\mathrm{j}} \exp (\mathrm{x}[\mathrm{j}])}\right)=-\mathrm{x}[\operatorname{class}]+\log \left(\sum_{\mathrm{j}} \exp (\mathrm{x}[\mathrm{j}])\right)$

　　https://blog.csdn.net/yyhaohaoxuexi/article/details/113824125

3.3 Probabilistic Contrastive Learning

　　本文不是設計一種新的資訊損失形式，而是關注如何通過構造一個新的輸入 $\mathbf{f}_{i}^{\prime}$ 來計算對比損失，使特徵 $f_i$ 接近類權重。也就是說，關於 $\mathbf{f}_{i}^{\prime}$ 的損失仍然是由

　　　　${\large \ell_{\mathbf{f}_{i}^{\prime}}=-\log \frac{\exp \left(s \mathbf{f}_{i}^{\prime} \tilde{\mathbf{f}}^{\prime}{ }_{i}\right)}{\sum_{j \neq i} \exp \left(s \mathbf{f}_{i}^{\prime} \mathbf{f}_{j}^{\prime}\right)+\sum_{k} \exp \left(s \mathbf{f}_{i}^{\prime \top} \tilde{\mathbf{f}}_{k}^{\prime}\right)} .} \quad\quad\quad(2)$

　　然後我們的目標是設計一個合適的 $\mathbf{f}_{i}^{\prime}$，這樣 $\ell_{\mathbf{f}_{i}^{\prime}}$ 越小，$f_i$ 就越接近類的權重。

　　從 Eq.2 中可知，$\ell_{\mathbf{f}_{i}^{\prime}}$ 越小，表示 $\mathbf{f}_{i}^{\prime \top} \tilde{\mathbf{f}}_{i}^{\prime}$ 越大。因此，上述問題可以粗略地簡化為 $\mathbf{f}_{i}^{\prime} \tilde{\mathbf{f}}_{i}^{\prime}$ 越大，$\mathbf{f}_{i}$ 越接近類權重。另一方面，如上文所解釋的，$\mathbf{f}_{i}$ 越接近類的權重，對應的概率 $p_i$ 就越接近 one-hot 形式，即滿足下面的形式：

　　　　$\mathbf{p}_{i}=(0, . ., 1, . ., 0) \quad\quad\quad(3)$

　　因此，我們的目標可以重新表述為如何設計一個合適的 $\mathbf{f}_{i}^{\prime}$，使 $\mathbf{f}_{i}^{\prime} \tilde{\mathbf{f}}^{\prime}{ }_{i}$ 越大，$\mathbf{p}_{i}$ 越接近Eq.3 中的 one-hot 形式。

　　幸運的是，本文發現概率 $\mathbf{p}_{i}$ 本身可以滿足這樣的要求。這裡我們來解釋一下細節。注意，$\mathbf{p}_{i}=\left(p_{i, 1}, \ldots, p_{i, C}\right)$ 和 $\tilde{\mathbf{p}}_{i}=\left(\tilde{p}_{i, 1}, \ldots, \tilde{p}_{i, C}\right)$ 都是概率分佈。然後我們有

　　　　$0 \leq p_{i, c} \leq 1,\quad 0 \leq \tilde{p}_{i, c} \leq 1,\quad \forall c \in\{1, \ldots, C\}\quad\quad\quad(4)$

　　此外，$\mathbf{p}_{i}$ 和 $\tilde{\mathbf{p}}_{i}$ 的 $\ell_{1}$-norm 等於 $1$ ，即：$\left\|\mathbf{p}_{i}\right\|_{1}=\sum_{c} p_{i, c}=1$ 、$\left\|\tilde{\mathbf{p}}_{i}\right\|_{1}=\sum_{c} \tilde{p}_{i, c}=1$。顯然，我們有

　　　　$\mathbf{p}_{i}^{\top} \tilde{\mathbf{p}}_{i}=\sum_{c} p_{i, c} \tilde{p}_{i, c} \leq 1\quad\quad\quad(5)$

　　等式成立的條件是 $\mathbf{p}_{i}= \tilde{\mathbf{p}}_{i}$，且 $\mathbf{p}_{i}$ 和 $\tilde{\mathbf{p}}_{i}$ 是 one-hot 形式。

　　從推導過程中，我們可以看到原型的概率的 1-範數等於 1 的性質是非常重要的。這一性質保證了只有當 $\mathbf{p}_{i}$ 和 $\tilde{\mathbf{p}}_{i}$ 同時滿足 one-hot 形式時，才能達到 $\mathbf{p}_{i}^{\top} \tilde{\mathbf{p}}_{i}$的最大值。顯然不能像 FCL 一樣在概率上使用 L2 範數了，最後，我們新的對比損失定義為

　　　　$\ell_{\mathbf{p}_{i}}=-\log \frac{\exp \left(s \mathbf{p}_{i}^{\top} \tilde{\mathbf{p}}_{i}\right)}{\sum_{j \neq i} \exp \left(s \mathbf{p}_{i}^{\top} \mathbf{p}_{j}\right)+\sum_{k} \exp \left(s \mathbf{p}_{i}^{\top} \tilde{\mathbf{p}}_{k}\right)}\quad\quad\quad(6)$

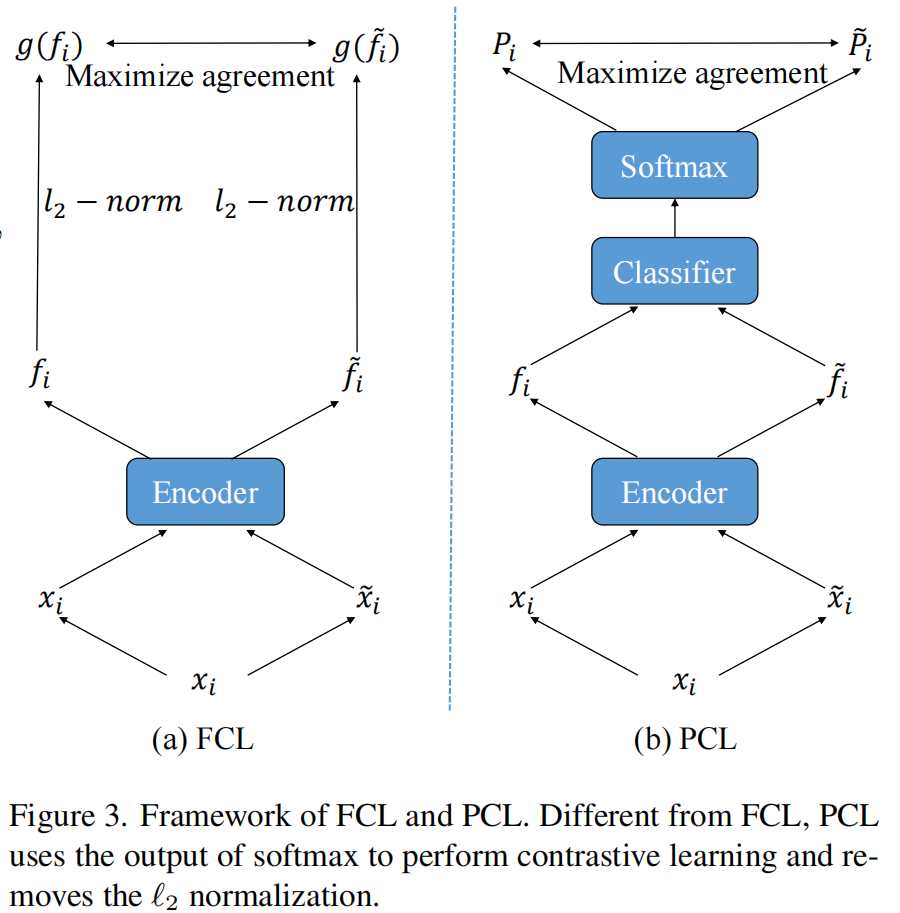
　　下圖給出 FCL 和 PCL 框架的對比：

4 Discussing: Is PCL a trick?

　　PCL非常簡單，看起來像是一個技巧。然而，這種簡單操作背後的原理是本文的核心價值。

　　1.目前的方法[51,52,82]通常將對比學習作為一種提高特徵一致性的一般技術，並經常關注假陰性樣本問題。很少有作品從減少特徵距離和類權重距離的角度來考慮對比學習。因此，我們有理由相信，這不是一個微不足道的觀點。

　　2.基於以上觀點，我們通過深入的分析，推匯出一個簡明的PCL。請注意，儘管PCL有點類似於投影頭，但它與投影頭有完全不同的動機。我們稍後還將證明，它不能從投影頭的角度自然地擴充套件到PCL。

　　3.如果沒有分析，我們就很難回答：為什麼PCL中涉及的兩個簡單操作如此重要？為什麼 logits+L2 normalization 不好？為什麼 probability + L2 normalization 的效果不好？

　　接下來，我們將證明一些常見的對比學習改進策略或自然泛化不能取代PCL在領域適應任務中的作用。

4.1 PCL v.s.FCL

　　先放一個結果：

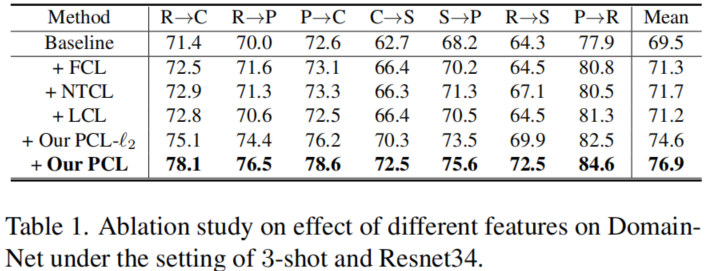
　　實驗發現：1) 傳統的 FCL 對比 Baseline 在結果上能有一定的提升，2) PCL 對比 FCL 能有 5% 的提升。

4.2 PCL v.s. FCL with Projection Head

　　SimCLR 證明了 Projection Head 是一個有用的技巧，本文思考能否將其用到 PCL 中，如下是三種 Projection Head：

　　① 在特徵上先使用一個非線性變換（nonlinear transformation，NT），然後使用 L2 normalization；【NT-Based Contrastive Learning (NTCL)】

　　② 直接使用分類器的輸出作為投影頭【 logits contrastive learning (LCL)】

　　③ 投影頭為 Classifier+softmax 【 PCL-L2】

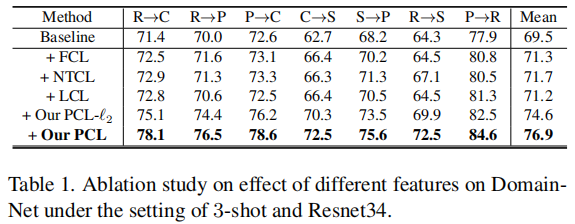
　　Table1 說明：

- 上述三個投影頭的效能都低於PCL，說明 PCL 增益的關鍵原因不是使用投影頭；　　
- LCL 和 PCL-L2 都不如 PCL，這說明簡單地引入類權重資訊並不能有效地強制執行類權重周圍的特徵定位；　　
- 實驗結果驗證了 PCL 的動機。目前的對比學習方法都遵循 Feature+L2 normalization 的標準正規化，且沒有理由採用概率的形式和移除 L2 normalization ；

4.3 PCL v.s. SFCL

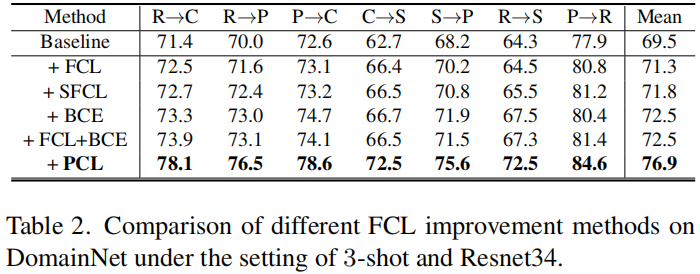
　　為解決假陰性樣本的問題，一個簡單的方向是監督對比學習 SFCL(supervised feature contrastive learning [26])，SFCL 要求使用標籤，以避免假陰性樣本。

　　Table 2顯示了結果。可以看出，SFCL 確實可以提高 FCL 的效能。然而，與 PCL 相比，SFCL 比 FCL 的改進非常有限。具體來說，SFCL 可以通過減輕假陰性問題來學習更好的特徵表示，但它不能解決特徵偏離類權值的問題，如FCL。實驗結果表明，特徵偏離類權值比負樣本問題對域自適應更為重要。

4.4 The Importance of InfoNCE Loss

　　在本節中，將探討是否有必要使用基於 InfoNC E損失的函數形式來近似的概率得到 one-hot 形式。特別地，考慮了二值交叉熵損失（BCE）。

　　　　$\ell_{b c e}=-\sum_{i, j, m, n}\left(\hat{y}_{i, j}^{n, m} \log \left(p_{i, j}^{n, m}\right)+\left(1-\hat{y}_{i, j}^{n, m}\right) \log \left(1-p_{i, j}^{n, m}\right)\right)\quad\quad\quad(6)$

　　為方便起見，記 $\mathbf{p}_{i}$ 和 $\tilde{\mathbf{p}}_{i}$ 分別為 $\mathbf{p}_{i}^{0}$、$\mathbf{p}_{i}^{1}$。

　　其中 $n, m \in\{0,1\}$，$p_{i, j}^{n, m}=\mathbf{p}_{i}^{n \top} \mathbf{p}_{j}^{m}$ ，$\hat{y}_{i, j}^{n, m}= \mathbb{1}\left [ p_{i, j}^{n, m} \geq t \quad \text{ or } \quad (i=j)\right] $，本文設定 $t=0.95$。

　　BCE loss 會最大化 $p_{i, j}^{n, m}=\mathbf{p}_{i}^{n \top} \mathbf{p}_{j}^{m}$ ，當 $\hat{y}_{i, j}^{n, m}=1$。$p_{i, j}^{n, m}$ 取最大當且僅當 $\mathbf{p}_{i}^{n}$、$\mathbf{p}_{j}^{m}$ 相等，且有 one-hot 形式。

4.5 T-SNE Visualization

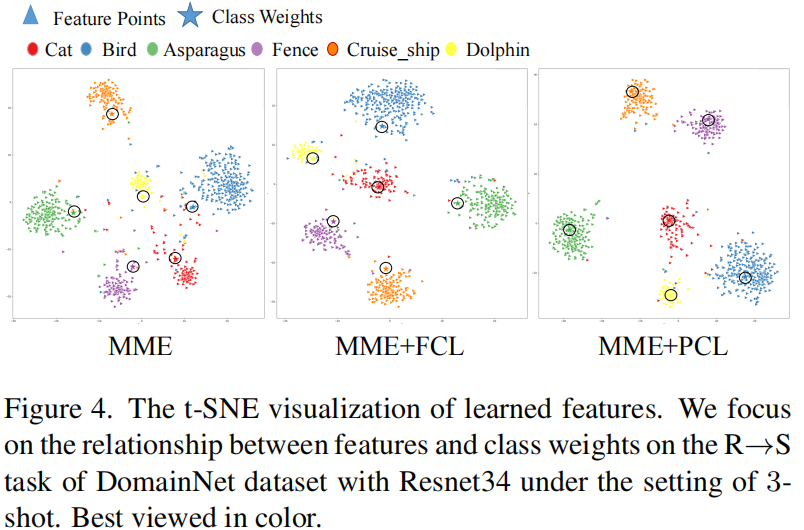
Note：

本人想找小夥伴一起學習，一起科研

計劃每週開個討論會（類似組會的形式），有感興趣的聯絡博主

論文解讀（PCL）《Probabilistic Contrastive Learning for Domain Adaptation》