Backbone 網路-ResNet v2 詳解

前言

本文的主要貢獻在於通過理論分析和大量實驗證明使用恆等對映（identity mapping）作為快捷連線（skip connection）對於殘差塊的重要性。同時，將 BN/ReLu 這些 activation 操作挪到了 Conv（真正的weights filter操作）之前，提出「預啟用「操作，並通過與」後啟用「操作做對比實驗，表明對於多層網路，使用了預啟用殘差單元（Pre-activation residual unit）的 resnet v2 都取得了比 resnet v1（或 resnet v1.5）更好的結果。

摘要

近期已經湧現出很多以深度殘差網路（deep residual network）為基礎的極深層的網路架構，在準確率和收斂性等方面的表現都非常引人注目。本文主要分析殘差網路基本構件（residual building block）中的訊號傳播，本文發現當使用恆等對映（identity mapping）作為快捷連線（skip connection）並且將啟用函數移至加法操作後面時，前向-反向訊號都可以在兩個 block 之間直接傳播而不受到任何變換操作的影響。同時大量實驗結果證明了恆等對映的重要性。本文根據這個發現重新設計了一種殘差網路基本單元（unit），使得網路更易於訓練並且泛化效能也得到提升。

注意這裡的實驗是深層 ResNet（$\geq$ 110 layers）的實驗，所以我覺得，應該是對於深層 ResNet，使用」預啟用」殘差單元（Pre-activation residual unit）的網路（ResNet v2）更易於訓練並且精度也更高。

1、介紹

深度殘差網路（ResNets）由殘差單元（Residual Units）堆疊而成。每個殘差單元（圖1 (a)）可以表示為：

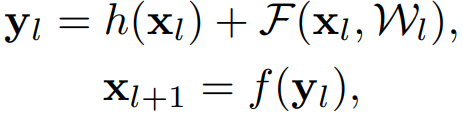
其中，$x_l$ 和 $x_{l+1}$ 是第 $l$ 個殘差單元的輸入和輸出，$F$ 是殘差函數。在 ResNet 中，$h(x_{l})= x_{l}$ 是恆等對映（identity），$f$ 是 ReLU 啟用函數。在 ImageNet 資料集和 COCO 資料集上，超過 1000 層的殘差網路都取得了當前最優的準確率。殘差網路的核心思想是在 $h(x_{l})$ 的基礎上學習附加的殘差函數 $F$，其中很關鍵的選擇就是使用恆等對映 $h(x_{l})= x_{l}$，這可以通過在網路中新增恆等快捷連線（skip connection) shortcut 來實現。

本文中主要在於分析在深度殘差網路中構建一個資訊「直接」傳播的路徑——不只是在殘差單元直接，而是在整個網路中資訊可以「直接」傳播。如果 $h(x_{l})$ 和 $f(y_{l})$ 都是恆等對映，那麼訊號可以在單元間直接進行前向-反向傳播。實驗證明基本滿足上述條件的網路架構一般更容易訓練。本文實驗了不同形式的 $h(x_{l})$，發現使用恆等對映的網路效能最好，誤差減小最快且訓練損失最低。這些實驗說明「乾淨」的資訊通道有助於優化。各種不同形式的 $h(x_{l})$ 見論文中的圖 1、圖2 和圖4 中的灰色箭頭所示。

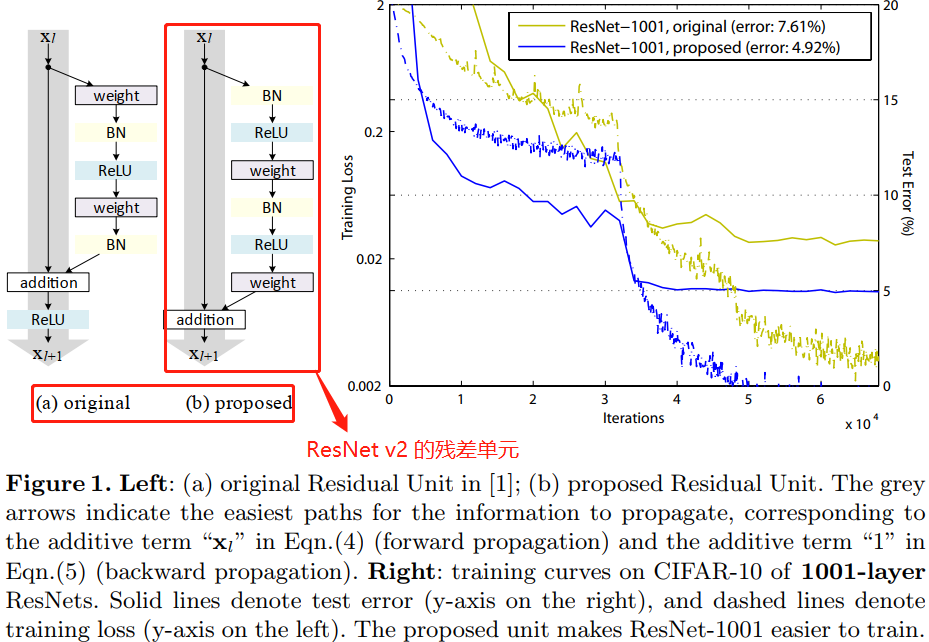
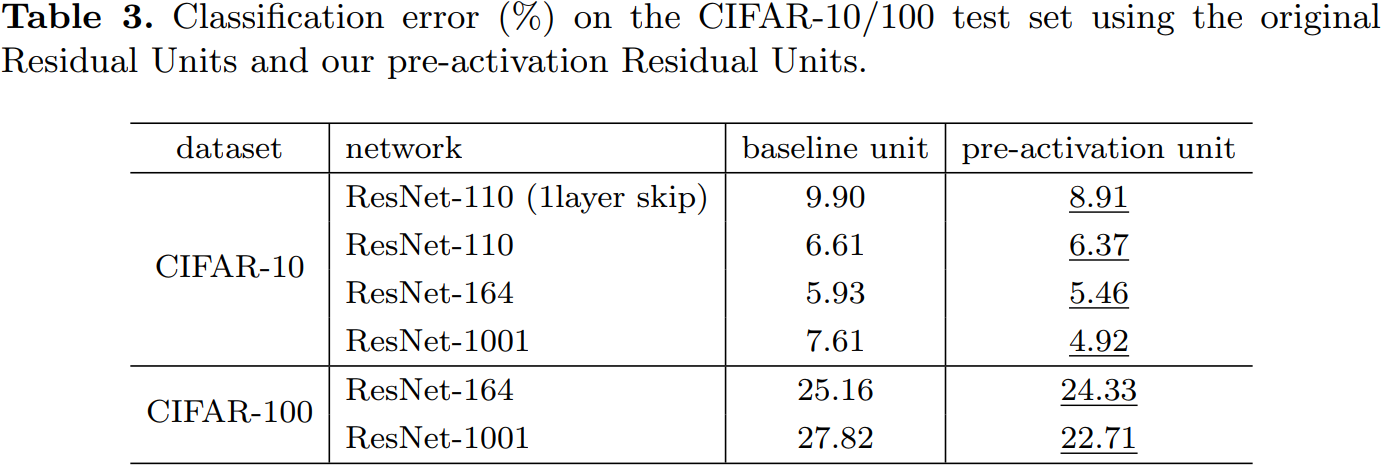
為了構建 $f(y_l)=y_l$ 的恆等對映，本文將啟用函數（ReLU 和 BN）移到權值層（Conv）之前，形成一種「預啟用（pre-activation）」的方式，而不是常規的「後啟用（post-activation）」方式，這樣就設計出了一種新的殘差單元（見圖 1(b)）。基於這種新的單元我們在 CIFAR-10/100 資料集上使用1001 層殘差網路進行訓練，發現新的殘差網路比之前（ResNet）的更容易訓練並且泛化效能更好。同時還考察了 200 層新殘差網路在 ImageNet 上的表現，原先的殘差網路在這個層數之後開始出現過擬合的現象。這些結果表明網路深度這個維度還有很大探索空間，畢竟深度是現代神經網路成功的關鍵。

2、深度殘差網路的分析

原先 ResNets 的殘差單元的可以表示為：

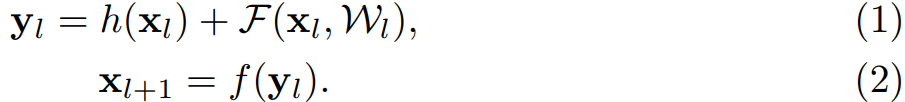
在 ResNet 中，函數 $h$ 是恆等對映，即 $h(x_{l}) = x_{l}$。公式的引數解釋見下圖：

如果函數 $f$ 也是恆等對映，即 $y_{l}\equiv y_{l}$，公式 (1)(2) 可以合併為：

那麼任意深層的單元 $L$ 與淺層單元 $l$之間的關係為：

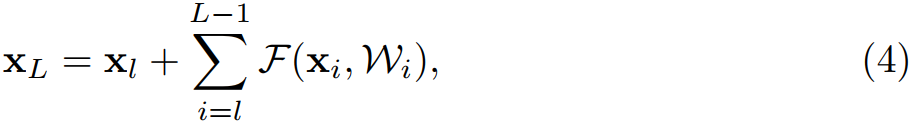
公式 (4) 有兩個特性：

深層單元的特徵可以由淺層單元的特徵和殘差函數相加得到；
任意深層單元的特徵都可以由起始特徵 $x_0$ 與先前所有殘差函數相加得到，這與普通（plain）網路不同，普通網路的深層特徵是由一系列的矩陣向量相乘得到。殘差網路是連加，普通網路是連乘。

公式 (4) 也帶來了良好的反向傳播特性，用 $\varepsilon $ 表示損失函數，根據反向傳播的鏈式傳導規則，反向傳播公式如下：

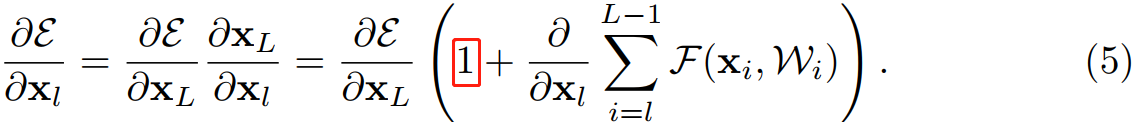
從公式 (5) 中可以看出，反向傳播也是兩條路徑，其中之一直接將資訊回傳，另一條會經過所有的帶權重層。另外可以注意到第二項的值在一個 mini-batch 中不可能一直是 -1，也就是說回傳的梯度不會消失，不論網路中的權值的值再小都不會發生梯度消失現象。

3、On the Importance of Identity Skip Connection

考慮恆等對映的重要性。假設將恆等對映改為 $h(x_{l}) = \lambda_{l}x_{l})$，則：

像公式 (4) 一樣遞迴的呼叫公式 (3)，得：

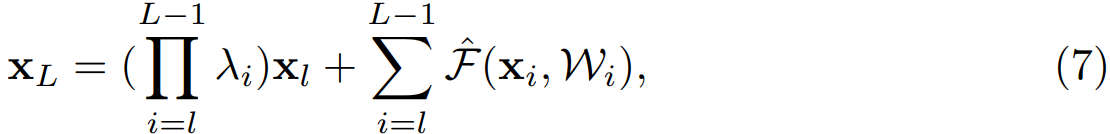
其中，$\hat{F}$ 表示將標量合併到殘差函數中，與公式 (5) 類似，反向傳播公式如下：

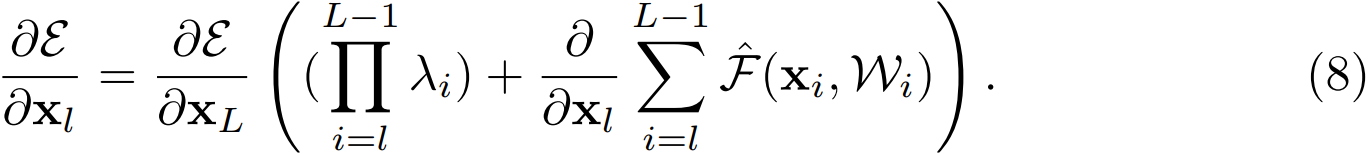
與公式 (5) 不同，公式 (8) 的第一個加法項由因子 $\prod_{i=l}^{L-1}\lambda_{i}$ 進行調節。對於一個極深的網路($L$ 極大)，考慮第一個連乘的項，如果所有的 $\lambda$ 都大於 1，那麼這一項會指數級增大；如果所有 $\lambda$ 都小於 1，那麼這一項會很小甚至消失，會阻斷來自 shortcut 的反向傳播訊號，並迫使其流過權重層。本文通過實驗證明這種方式會對模型優化造成困難。

另外其他不同形式的變換對映也都會阻礙訊號的有效傳播，進而影響訓練程序。

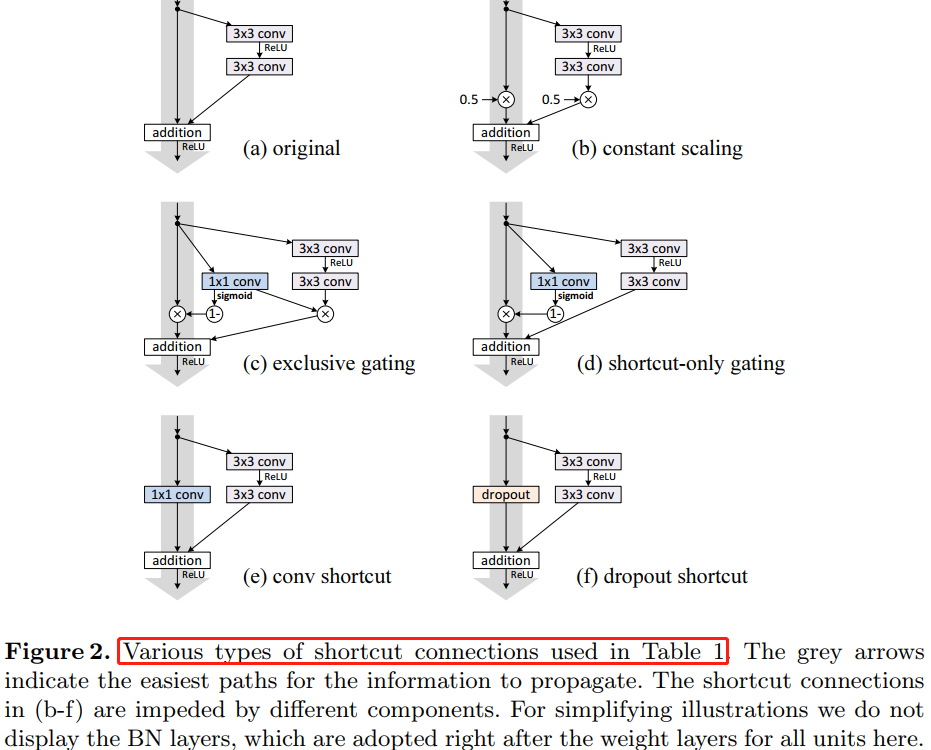
4、On the Usage of Activation Functions

第 3 章考察使用不同形式對映（見圖 2）來驗證函數 $h$ 是恆等對映的重要性，這章討論公式(2)中的 $f$，如果 $f$ 也是恆等對映，網路的效能會不會有所提升。通過調節啟用函數 (ReLU and/or BN) 的位置，來使 $f$ 是恆等對映。圖 4 展示了啟用函數在不同位置的殘差單元結構圖去。

圖 4(e) 的」預啟用「操作是本文提出的一種對於深層殘差網路能夠更有效訓練的網路結構（ResNet v2）。

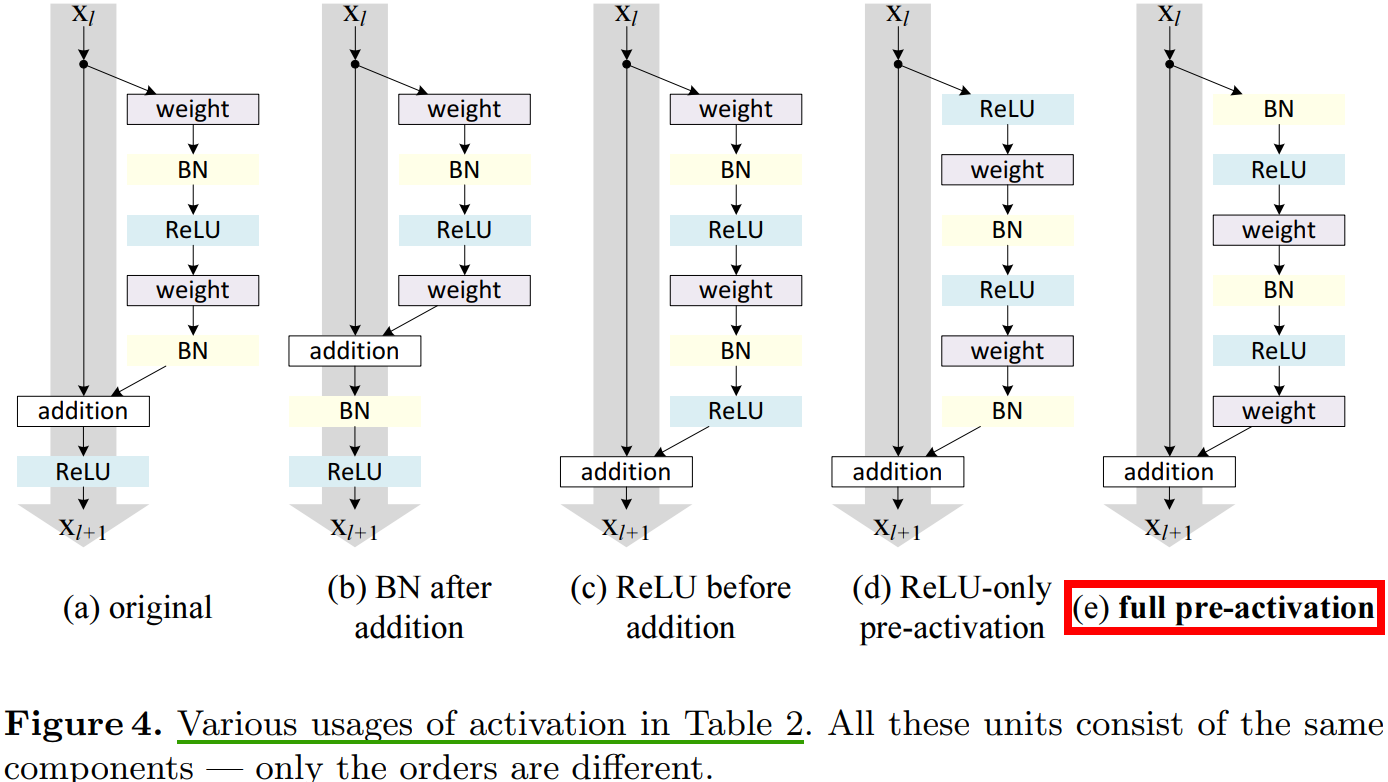
4.1、Experiments on Activation

本章，我們使用 ResNet-110 和 164 層瓶頸結構(稱為 ResNet-164)來進行實驗。瓶頸殘差單元包含一個 $1\times 1$ 的層來降維，一個 $3\times 3$ 的層，還有一個 $1\times 1$ 的層來恢復維度。如 ResNet 論文中描述的那樣，它的計算複雜度和包含兩個 $3\times 3$ 折積層的殘差單元相似。

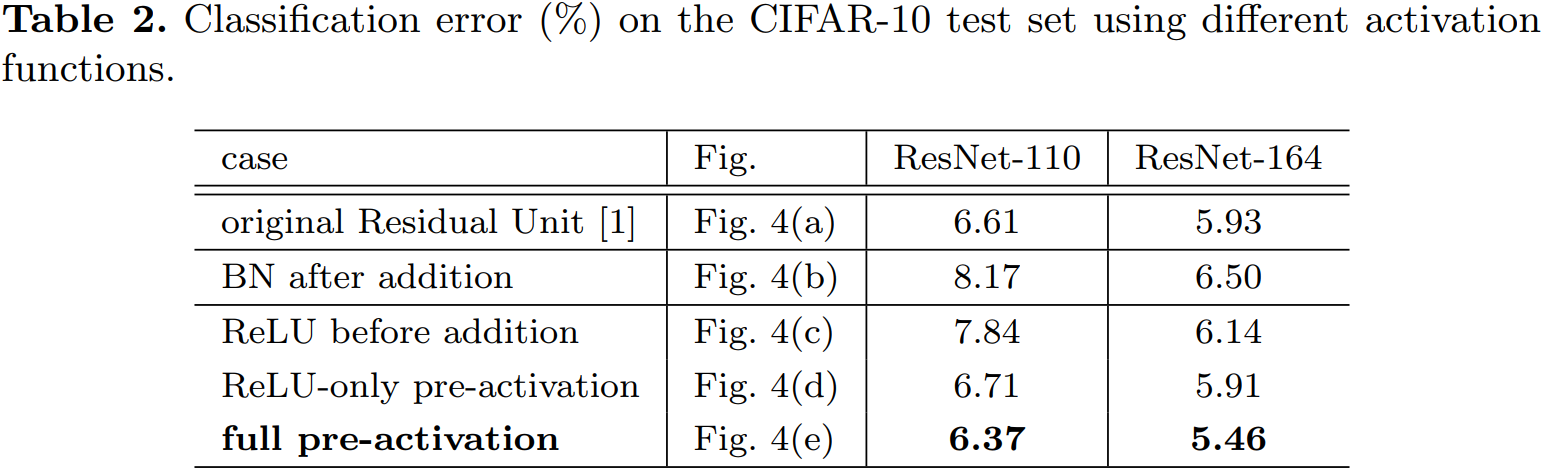
BN after addition
效果比基準差，BN 層移到相加操作後面會阻礙訊號傳播，一個明顯的現象就是訓練初期誤差下降緩慢。

ReLU before addition
這樣組合的話殘差函數分支的輸出就一直保持非負，這會影響到模型的表示能力，而實驗結果也表明這種組合比基準差。

Post-activation or pre-activation
原來的設計中相加操作後面還有一個 ReLU 啟用函數，這個啟用函數會影響到殘差單元的兩個分支，現在將它移到殘差函數分支上，快捷連線分支不再受到影響。具體操作如圖 5 所示。

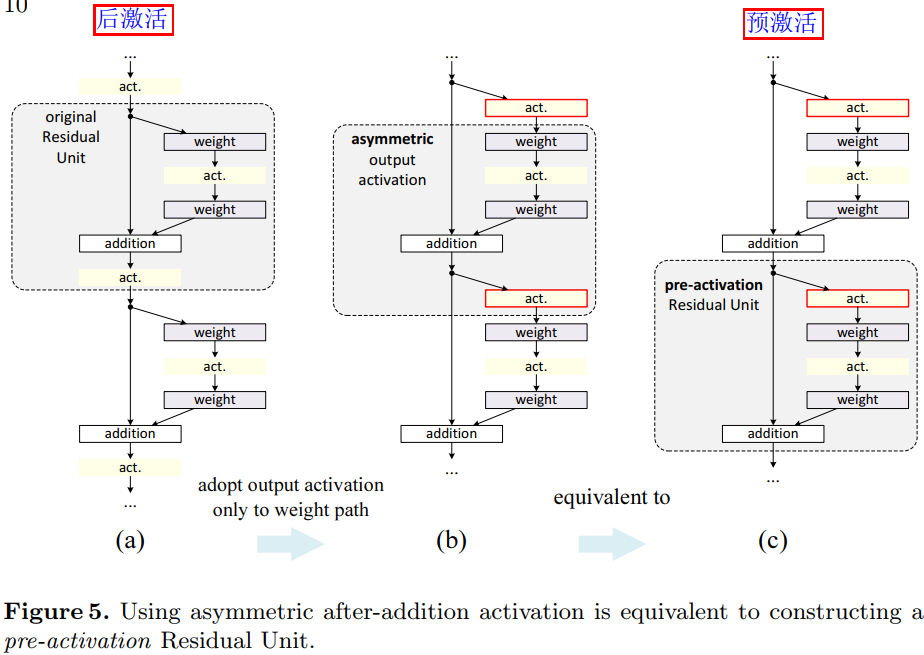
根據啟用函數與相加操作的位置關係，我們稱之前的組合方式為「後啟用（post-activation）」，現在新的組合方式稱之為「預啟用（pre-activation）」。原來的設計與預啟用殘差單元之間的效能對比見表 3。預啟用方式又可以分為兩種：只將 ReLU 放在前面，或者將 ReLU 和 BN都放到前面，根據表 2 中的結果可以看出 full pre-activation 的效果要更好。

4.2、Analysis

使用預啟用有兩個方面的優點：1) $f$ 變為恆等對映，使得網路更易於優化；2)使用 BN 作為預啟用可以加強對模型的正則化。

Ease of optimization
這在訓練 1001 層殘差網路時尤為明顯，具體見圖 1。使用原來設計的網路在起始階段誤差下降很慢，因為 $f$ 是 ReLU 啟用函數，當訊號為負時會被截斷，使模型無法很好地逼近期望函數；而使用預啟用網路中的 $f$ 是恆等對映，訊號可以在不同單元直接直接傳播。本文使用的 1001層網路優化速度很快，並且得到了最低的誤差。

$f$ 為 ReLU 對淺層殘差網路的影響並不大，如圖 6-right 所示。本文認為是當網路經過一段時間的訓練之後權值經過適當的調整，使得單元輸出基本都是非負，此時 $f$ 不再對訊號進行截斷。但是截斷現象在超過 1000層的網路中經常發生。

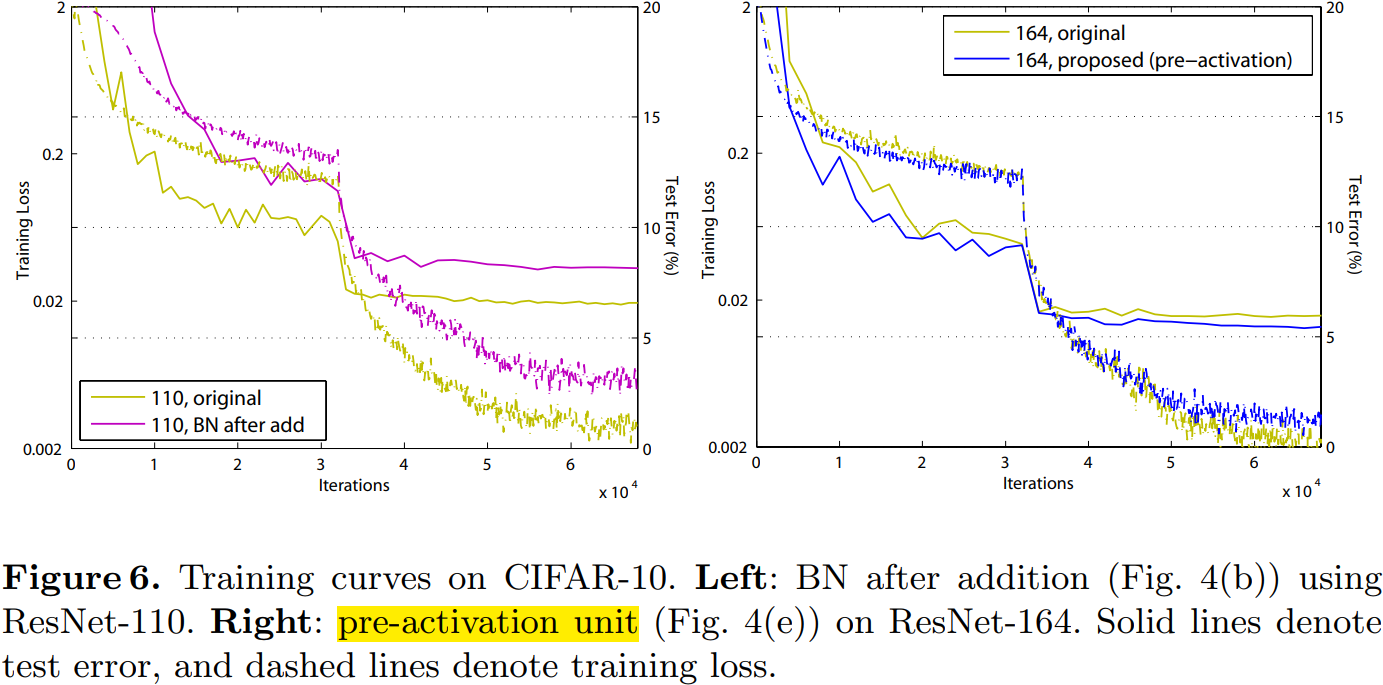
Reducing overfitting
觀察圖 6-right，使用了預啟用的網路的訓練誤差稍高，但卻得到更低的測試誤差，本文推測這是 BN 層的正則化效果所致。在原始殘差單元中，儘管BN 對訊號進行了標準化，但是它很快就被合併到捷徑連線(shortcut)上，組合的訊號並不是被標準化的。這個非標準化的訊號又被用作下一個權重層的輸入。與之相反，本文的預啟用（pre-activation）版本的模型中，權重層的輸入總是標準化的。

5、Results

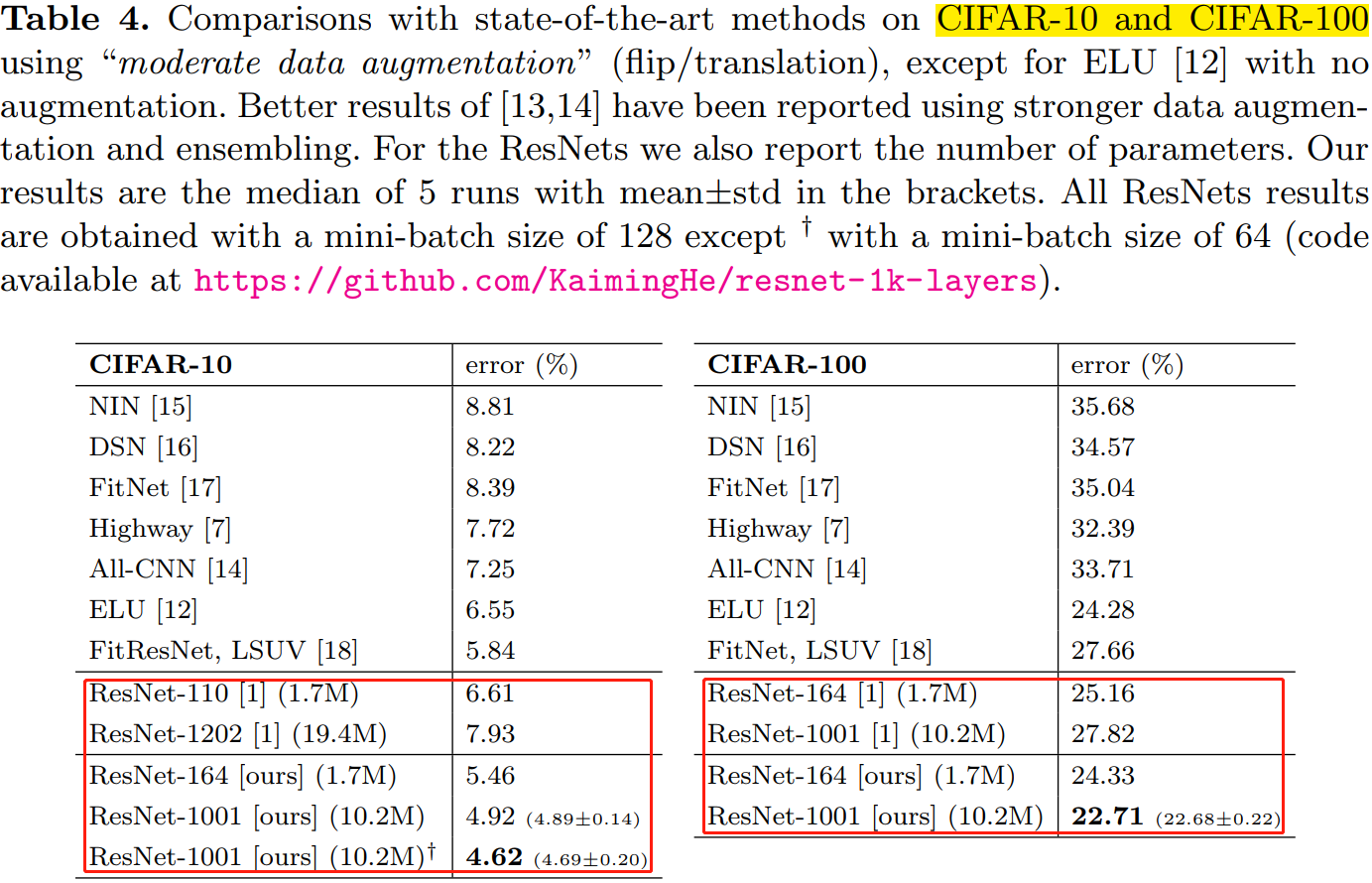
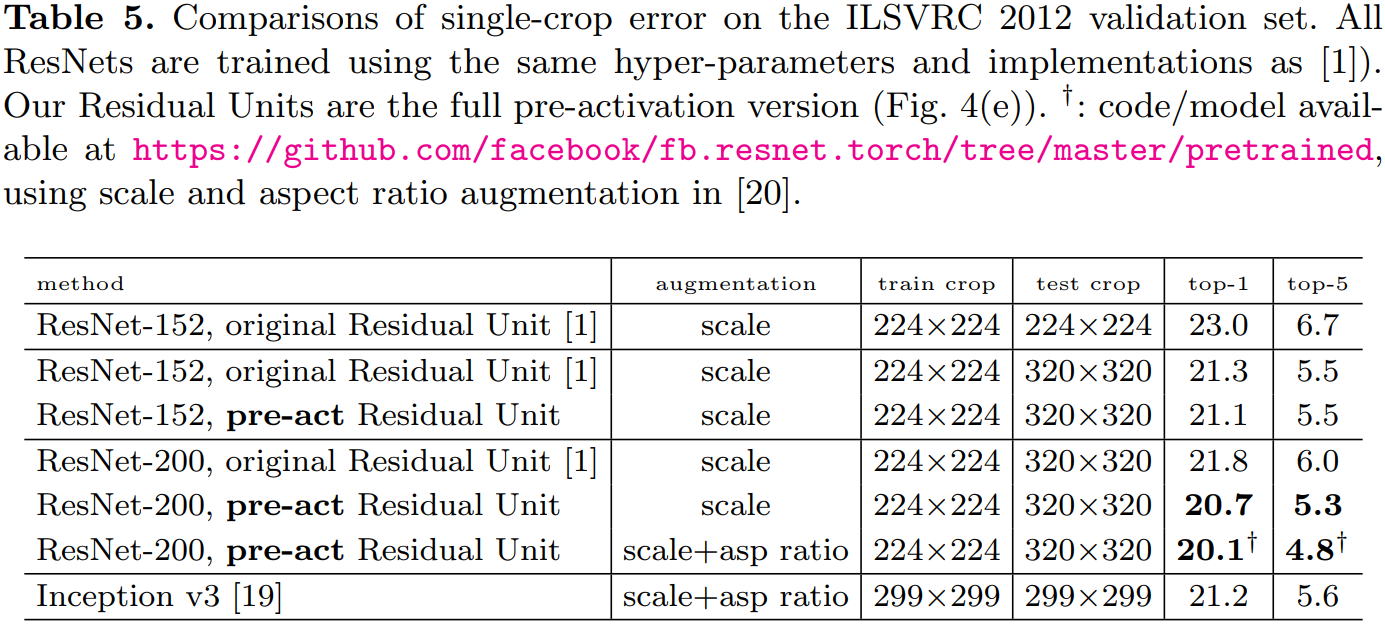
表 4、表 5 分別展示了不同深層網路在不同資料集上的表現。使用的預啟用單元的且更深層的殘差網路（ResNet v2）都取得了最好的精度。

6、結論

恆等對映形式的快捷連線和預啟用對於訊號在網路中的順暢傳播至關重要。