WeetCode3 暴力遞迴->記憶化搜尋->動態規劃
筆者這裡總結的是一種套路,這種套路筆者最先是從左程雲的b站視訊學習到的
本文進行簡單總結
一丶動態規劃的思想
使用dp陣列記錄之前狀態計算的最佳結果,找出當前狀態和之前狀態的關係(狀態轉移方程)然後使用狀態轉移方程,計算處當前狀態最佳結果,然後更新dp陣列,填完dp陣列即得到最佳結果
本質是空間換時間
二丶動態規劃的難點
狀態轉移方程,這個概念比較難理解,更難想出具體題目的狀態轉移方程
本文就是為了解決這種痛點
我們從暴力遞迴寫起,然後優化成記憶化搜尋,然後根據遞迴大任務和小任務的關係,得到狀態轉移方程,優化成動態規劃。
三丶暴力遞迴->記憶化搜尋->動態規劃
1.從一道題說起
現在存在一個機器人,整數N表示存在N個位置,機器人可以位於1~N上的任意一個位置,
S位機器人初始位置(當然N>=S>=1)E表示機器人的目標位置,K表示機器人可以走多少步,機器人必須走完K步,只能向左or向右且不可以停留在一個位置不走,請問機器人從S到E右多少中走法
例如N=5 機器人可以位於【1,2,3,4,5】S=2,機器人起始位於2,E=4 機器人目標位置位4,機器人必須走完K=4
存在可行方案:
2->3->4->5->4
2->3->4->3->4
2->3->2->3->4
2->1->2->3->4
- 第一反應:純純動態規劃,開始找狀態轉移方程,如何找到狀態轉移方程不是本文的重點我們從暴力遞迴講起
2.暴力遞迴解題
暴力遞迴的關鍵是如何【嘗試】,嘗試依賴於刷題的經驗
-
分析:
- 如果機器人當前還有剩餘步數要走
- 機器人位於1位置,它只能向右,因為只能位於1~N位置上
- 如果機器人位於N位置,它只能向左,因為只能位於1~N位置上
- 如果機器人位於2~N-1位置,它可以向左or向右
當然每走一步剩餘步數需要減1- 如果機器人當前沒有剩餘部署要走
- 如果機器人走到了目標位置,我們返回1,因為這是一種可行的機器人移動方案
- 如果機器人當前不在目標位置,因為沒有步數走,還不在目標位置,說明這樣走不可行
- 如果機器人當前還有剩餘步數要走
-
根據分析寫出暴力遞迴方法
- 我們可以知道遞迴出口baseCase位當前剩餘步數等於0,無論是否在目標位置,我們都將返回0,1,因為無路可走
- 當機器人位於1 or N的時候只可以向右or向左
- 機器人位於中間位置,存在兩個方向,可以向左和向右
/** * @param N 1~N可以停留 * @param S 機器人起始位置 * @param E 機器人目標位置 * @param K 總步數 * @return int 總共的走法 */ public static int moveWayCount(int N, int S, int E, int K) { return Recursion.recursion(N, S, E, K); } /**** * 遞迴怎麼做 */ static class Recursion { /** * @param N 1~N可以停留 * @param curIndex 機器人當前位置 * @param E 機器人目標位置 * @param resetStep 剩餘步數 * @return int 總共的走法 */ static int recursion(int N, int curIndex, int E, int resetStep) { //遞迴出口baseCase位當前剩餘步數等於0,無論是否在目標位置,我們都將返回0,1,因為無路可走 if (resetStep == 0) { if (curIndex == E) { return 1; } else { return 0; } } //當機器人位於1orN的時候只可以向右or向左 if (curIndex == 1) { return recursion(N, 2, E, resetStep - 1); } if (curIndex == N) { return recursion(N, N - 1, E, resetStep - 1); } //機器人位於中間位置,存在兩個方向,可以向左和向右 return recursion(N, curIndex + 1, E, resetStep - 1) + recursion(N, curIndex - 1, E, resetStep - 1); } }其實還可以加一個剪枝條件,如果當前的步數那怕機器人向著目標地點一直前進都無法到達那麼直接返回0(Math.abs(curIndex-E)<restStep 直接返回0) 但是這個不是本文的關鍵,遂不表於程式碼中 -
時間複雜度分析,如果機器人位於中間位置,遞迴樹是一個二元樹,樹的高度是K,因為需要走K步,那麼時間複雜度2的k次冪
-
空間複雜度,遞迴樹高度位K,O(K)
-
如何優化
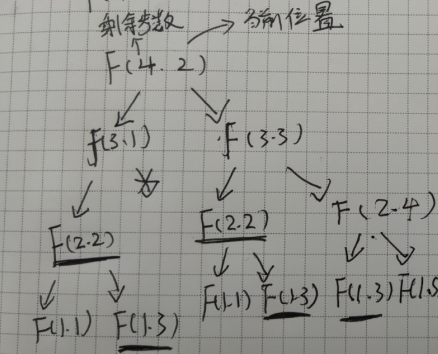
- 觀察上面的遞迴樹(沒有畫到葉子節點,但是足以說明問題)
- 我們進行了重複的計算 F(3,1)和F(3,3)都依賴了F(2,3)
- 我們可以使用使用快取在減少重複計算,具體見【三丶記憶化搜尋】
- 觀察上面的遞迴樹(沒有畫到葉子節點,但是足以說明問題)
3.記憶化搜尋解題
-
記憶化搜尋的思想:使用快取減少遞迴的重複計算
-
觀察上面的遞迴方法的方法簽名:
int recursion(int N, int curIndex, int E, int resetStep)N和E是兩個固定的引數,遞迴方法返回值取決於curIndex,和resetStep
- curIndex的大小範圍是1~N
- resetStep的大小範圍時0~K
-
所以我們只需要使用一個一個(N+1)*(K+1)的二位陣列來快取遞迴的答案
如果答案已經有了,那我們直接取陣列的值,反之遞迴求答案,寫答案到陣列中即可(當然你也可以使用map來快取答案,但是為了更好過渡到動態規劃的解法,我們這裡使用二維陣列)
-
-
程式碼:
/** * @param N 1~N可以停留 * @param S 機器人起始位置 * @param E 機器人目標位置 * @param K 總步數 * @return int 總共的走法 */ public static int moveWayCount(int N, int S, int E, int K) { // return Recursion.recursion(N, S, E, K); int[][] memory = new int[N + 1][K + 1]; for (int row = 0; row < memory.length; row++) { Arrays.fill(memory[row], -1); } return MemorySearch.recursion(N, S, E, K, memory); } /**** * 記憶化搜尋 */ static class MemorySearch { /** * @param N 1~N可以停留 * @param curIndex 機器人當前位置 * @param E 機器人目標位置 * @param resetStep 剩餘步數 * @param memory 優化遞迴的記憶陣列 * @return int 總共的走法 */ static int recursion(int N, int curIndex, int E, int resetStep, int[][] memory) { int res; if (resetStep == 0) { if (curIndex == E) { return 1; } else { return 0; } } //如果沒有命中快取 if (memory[curIndex][resetStep] == -1) { //求值 if (curIndex == 1) { res = recursion(N, 2, E, resetStep - 1, memory); } else if (curIndex == N) { res = recursion(N, N - 1, E, resetStep - 1, memory); } else { res = recursion(N, curIndex + 1, E, resetStep - 1, memory) + recursion(N, curIndex - 1, E, resetStep - 1, memory); } //寫快取 memory[curIndex][resetStep] = res; } else { //命中快取 返回快取內容即可 res = memory[curIndex][resetStep]; } return res; } } -
時間複雜度,我們一共求解了N*K次來填滿memory陣列,每一次求解的時間複雜度O(1)總時間複雜度O(NxK)
-
空間複雜度,O(NxK)
4.動態規劃解題
-
寫在前面,和記憶化搜尋相比動態規劃並沒有時間複雜度,空間複雜度的提升,只是更專注於狀態的轉移
-
如何改成動態規劃
應該敏感的知道這題可以用動態規劃,定義一個 int[][] dp = new int[N + 1][K + 1];作為dp陣列-
從暴力遞迴獲取狀態轉移的規律
這個圖方便理解,如何推出的看下方
-
如何初始化dp陣列
if (resetStep == 0) { if (curIndex == E) { return 1; } else { return 0; } } //從這段程式碼我們可以知道dp的第一行除了E那一列全為0, //只有dp[0][E]=1 -
第一個狀態轉移方程
if (curIndex == 1) { return recursion(N, 2, E, resetStep - 1)s; } //可以知道當 位於第一列的時候,dp[1][剩餘步數]=dp[2][剩餘步數-1],也就是右上角的值 -
第二個狀態轉移方程
if (curIndex == N) { return recursion(N, N - 1, E, resetStep - 1); } //可以知道當 位於第N列的時候,dp[N-1][剩餘步數]=dp[2][剩餘步數-1] 也就左上角的值 -
第三個狀態轉移方程
//機器人位於中間位置,存在兩個方向,可以向左和向右 return recursion(N, curIndex + 1, E, rzesetStep - 1) + recursion(N, curIndex - 1, E, resetStep - 1); //當不位於 【邊界】的時候 //recursion(N, curIndex + 1, E, resetStep - 1) 右上角的值 //recursion(N, curIndex - 1, E, resetStep - 1)左上角 //如果 curIndex!=1 and curIndex!=N //dp[curIndex][剩餘步數]=dp[curIndex+1][剩餘步數-1]+dp[curIndex-1][剩餘步數-1]
-
-
-
程式碼:
static class DynamicProgramming { /** * @param N 1~N可以停留 * @param S 機器人起始位置 * @param E 機器人目標位置 * @param K 總步數 * @return int 總共的走法 */ static int dynamicProgramming(int N, int S, int E, int K) { int[][] dp = new int[K + 1][N + 1]; dp[0][E] = 1; for (int restStep = 1; restStep <= K; restStep++) { for (int cur = 1; cur <= N; cur++) { if (cur == 1) { dp[restStep][cur] = dp[restStep - 1][2]; continue; } else if (cur == N) { dp[restStep][cur] = dp[restStep - 1][N - 1]; continue; } dp[restStep][cur] = dp[restStep - 1][cur + 1] + dp[restStep - 1][cur - 1]; } } return dp[K][S]; } }
至此,我們可以看出遞迴,記憶化搜尋,動態規劃,具備一定的聯絡
5.遞迴改動態規劃的套路
- 難點在,如何【嘗試】怎麼可以相到一個合理的嘗試方式並且寫出遞迴程式碼
- 如何改動態規劃
- 看遞迴方法可變引數的個數,這個可變引數的個數決定了dp陣列的大小和維度
- 看呼叫遞迴的方法的入入參,可以知道我們的最終目的是dp中的哪一項
- 根據遞迴的baseCase初始化dp陣列
- 根據遞迴中當前方法棧的返回值依賴於哪些遞迴的返回值,根據這個我們可以得到狀態轉移方程,
- 根據當前位置依賴於哪些位置,可以知道動態規劃for迴圈怎麼寫,從上到下,還是從下到上,從左到右還是從右到左
四丶使用套路解幾道題
1.換錢最少的貨幣數
【題目】
給定陣列arr, arr中所有的值都為正數且不重複。每個值代表一種面值的貨幣,每種面值的貨幣可以使用任意張,
再給定一個整數aim,代表要找的錢數,求組成aim的最少貨幣數。
【舉例】
arr=[5,2,3],aim=20
4張5元可以組成20元,其他找錢方案都要使用更多的貨幣,所以返回4.
arr=[5,2,3],aim=0
不用任何貨幣就可以組成0元,返回0
arr=[3,5],aim=2
根本沒法組成2元,錢不能找開的情況下預設返回-1.
-
暴力遞迴
/**** * 遞迴解法 */ static class Recursion { /*** * 最少使用多少張 amountArray 中錢才能湊出目標錢 * @param amountArray 貨幣陣列 * @param targetMoneyToChange 目標湊成錢 * @return 最少使用幾張 */ static int minAmountMoneyToChange(int[] amountArray, int targetMoneyToChange) { return recursion(amountArray, 0, targetMoneyToChange); } /*** * 對當前錢的選擇做出抉擇 * 可以選擇不選擇當前的錢,也可以選擇當前的錢,取小者 * 如果選擇當前錢,無法湊出目標錢數 那麼返回-1 * @param amountArray 貨幣陣列 * @param nowChooseIndex 當前選擇到amountArray的那個位置的硬幣 * @param restMoney 剩餘的需要湊出來的錢 * @return 當前決策最少需要多少張(可以選擇不選擇當前的錢,也可以選擇當前的錢,取小者) */ static int recursion(int[] amountArray, int nowChooseIndex, int restMoney) { //當前剩餘的錢為0 if (restMoney == 0) { //返回0 表示不選擇當前位置的錢,所以選擇對湊出目標錢數的影響是0 return 0; } if (restMoney < 0) { //如果restMoney小於0 說明選擇的錢太多了,之前做的選擇是錯誤的 return -1; } //如果當前選擇的已經到達貨幣陣列的極限 沒有辦法選擇更多的錢了 if (nowChooseIndex >= amountArray.length) { return -1; } //能走到這兒說明 剩餘的錢不為0,也不為負數,且還有選擇的機會 //如果不選擇當前的錢 選擇的位置+1(向後做出選擇)剩餘的前數不變因為我們不選擇當前的錢 int noChooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney); //選擇當前的錢 剩餘錢減少當前選擇錢的面值 int chooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney - amountArray[nowChooseIndex]); //無論是否選擇當前錢 or 不選擇當前錢,都木有辦法湊出目標錢 那麼返回-1 //如100,200,300,湊5,選擇100 or不選擇100都沒法湊出5返回-1 if (noChooseNow == -1 && chooseNow == -1) { return -1; } //如果不選擇當前錢,我們再也無法湊出來目標面值的錢 //比如2 100 3湊5 如果放棄了2我們再也沒有辦法湊出5元錢了 所以我們必須持有這張2 if (noChooseNow == -1) { //那麼我們必須做出選擇當前錢的抉擇,選擇當前錢那麼+1(因為選擇了當前錢,張數+1) return chooseNow + 1; } //選擇當前錢了我們再也無法湊出目標錢 那麼我們只能做出不選擇當前錢的抉擇 //比如 100,2,3湊出5 選擇了100我們不可能湊出5了 我們只能放棄100 if (chooseNow == -1) { return noChooseNow; } //反之我們可以選擇選當前錢,可以 不選擇當前錢,因為找最少的貨幣數 //那麼取較小者 return Math.min(chooseNow + 1, noChooseNow); } } -
記憶化搜尋
觀察上述遞迴方法
static int recursion(int[] amountArray, int nowChooseIndex, int restMoney) { int[] amountArrays是一個不會變化的陣列(選擇的時候還改變這個錢那就是來搗亂的) nowChooseIndex 介於 0~amountArrays.length-1 restMoney介於0~目標湊出來的錢數 需要說明的是 restMoneny可以到達負數,但是負數是固定返回-1的so記憶化搜尋需要的陣列只需要是一個二維陣列 or使用hashMap 這個題使用hashMap效果可能更好,因為 restMoney 的值取決於amountArray,比如amountArray=【5,10,20】目標錢為15,restMoney永遠不可能到達1 2 3這些數目,所以使用二位陣列存在浪費,當前最壞情況空間複雜度一樣 如果使用陣列 那麼陣列需要被初始化為-2,因為-1是無效解,0是有效解,所以使用-2具體程式碼沒啥難度不寫了
-
動態遞迴
我們需要根據遞迴的程式碼推斷出狀態轉移方程
使用amountArray=【2,3,5,7,2】targetMoneyToChange=10為例子-
我們的目標是什麼
return recursion(amountArray, 0, targetMoneyToChange); 目標是dp[0][10] -
dp陣列的大小
int[][]dp=new int[amountArray.length+1][targetMoneyToChange+1] //因為存在行越界的情況,錢10的意義是restMoney=10 是具有意義的 //new int[6][11] -
如何初始化dp陣列
1.第一列置為0
//當前剩餘的錢為0 if (restMoney == 0) { //返回0 表示不選擇當前位置的錢,所以選擇對湊出目標錢數的影響是0 return 0; }2.列小於0一律返回-1
if (restMoney < 0) { //如果restMoney小於0 說明選擇的錢太多了,之前做的選擇是錯誤的 return -1; }3.行大於等於amountArray.length一律返回-1
其實我們dp陣列行大小為amountArray.length+1,去到amountArray.length+1後序不為++,所以這一句其實是把最後一行置為-1,到底是程式碼邏輯處理這個情況,還是多弄一行,取決於dp陣列如何設計
//如果當前選擇的已經到達貨幣陣列的極限 沒有辦法選擇更多的錢了 if (nowChooseIndex >= amountArray.length) { return -1; } -
狀態轉移
假如當前restMoney=6 nowChooseIndx=2
int noChooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney); int chooseNow = recursion(amountArray, nowChooseIndex + 1, restMoney - amountArray[nowChooseIndex]);依賴於 nowChooseIndex + 1,restMoney的值也就是 dp【3】【6】的值
依賴nowChooseIndex+1,restMoney - amountArray[nowChooseIndex]的值
也就是dp【3】【6-amountArray[2]】的值,
總而言之,當前行的求解依賴於下一行,當前列的求解依賴於左邊列,左邊第幾列需要從amountArray中取
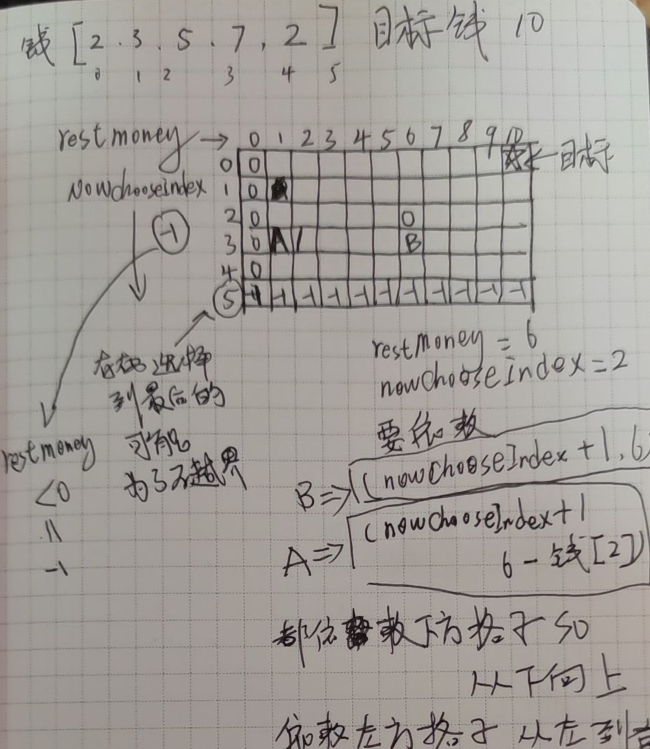
寫程式碼發現dp【5】【0】不可以設定為-1 因為這個位置表示的是剩餘錢為0,當前選到最後一個貨幣,這是一個可行解,他喵的害我還久debug不出來
-
程式碼
/*** * 最少使用多少張 amountArray 中錢才能湊出目標錢 * @param amountArray 貨幣陣列 * @param targetMoneyToChange 目標湊成錢 * @return 最少使用幾張 */ static int minAmountMoneyToChange(int[] amountArray, int targetMoneyToChange) { int len = amountArray.length; int[][] dp = new int[len + 1][targetMoneyToChange + 1]; //初始化 Arrays.fill(dp[0], 0); for (int col = 1; col < targetMoneyToChange + 1; col++) { dp[len][col] = -1; } System.out.println(ArrayUtils.toString(dp)); for (int nowChooseIndex = len - 1; nowChooseIndex >= 0; nowChooseIndex--) { for (int restMoney = 1; restMoney <= targetMoneyToChange; restMoney++) { // int noChooseNow = valueInAmountArray(dp, nowChooseIndex + 1, restMoney); // int chooseNow = valueInAmountArray(dp, nowChooseIndex + 1, restMoney - amountArray[nowChooseIndex]); // dp[nowChooseIndex][restMoney] = doPolicyDecision(noChooseNow, chooseNow); int noChooseNow = dp[nowChooseIndex + 1][restMoney]; int chooseNow = -1; if (restMoney - amountArray[nowChooseIndex] >= 0) { chooseNow = dp[nowChooseIndex + 1][restMoney - amountArray[nowChooseIndex]]; } if (noChooseNow == -1 && chooseNow == -1) { dp[nowChooseIndex][restMoney] = -1; continue; } //如果不選擇當前錢,我們再也無法湊出來目標面值的錢 //比如2 100 3湊5 如果放棄了2我們再也沒有辦法湊出5元錢了 所以我們必須持有這張2 if (noChooseNow == -1) { //那麼我們必須做出選擇當前錢的抉擇,選擇當前錢那麼+1(因為選擇了當前錢,張數+1) dp[nowChooseIndex][restMoney] = chooseNow + 1; continue; } //選擇當前錢了我們再也無法湊出目標錢 那麼我們只能做出不選擇當前錢的抉擇 //比如 100,2,3湊出5 選擇了100我們不可能湊出5了 我們只能放棄100 if (chooseNow == -1) { dp[nowChooseIndex][restMoney] = noChooseNow; continue; } //反之我們可以選擇選當前錢,可以 不選擇當前錢,因為找最少的貨幣數 //那麼取較小者 dp[nowChooseIndex][restMoney] = Math.min(chooseNow + 1, noChooseNow); } } System.out.println(ArrayUtils.toString(dp)); return dp[0][targetMoneyToChange]; }
-
2.馬踏棋盤
中國象棋,可以想象成一個int[8][10]的二維陣列,馬棋子最開始位於(0,0)位置,去往目標位置(x,y)必須走step步,問一共存在多少種的走法
-
思路
從【0,0】使用step步到【x,y】等價於使用step-1步到【x-1,y+2】,【x+1,y+2】....(這些步驟再跳一步就可以到【x,y】了)
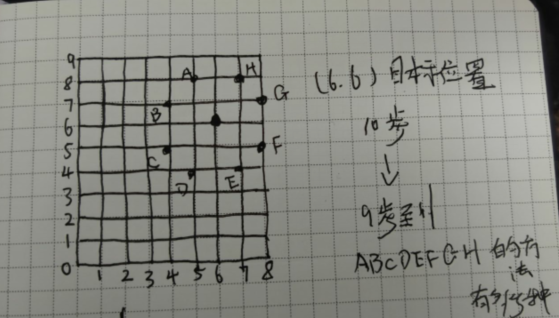
-
暴力遞迴
- baseCase:越界了那麼當前這種跳法不行。or 步數用完了如果當前位置是目標位置那麼返回1表示這是一種可行的跳法,反之返回0表示這個跳法不行
static class Recursion { static int horseJumpToTargetPosition(int x, int y, int step) { return recursion(x, y, step); } /*** * 起始位於0 0 去往目標位置 x y 必須走step步 * * 但是程式碼的寫法是從 x,y 跳向 0 ,0用step步 * 二者等價 * @param x 目標位置的橫座標 * @param y 目標位置的縱座標 * @param step 需要走多少步 * @return 一共多少中走法 */ static int recursion(int x, int y, int step) { //如果越界那麼說明當前遞迴樹的分支不得行 if (!checkPosition(x, y)) { return 0; } //如果步數用完了 if (step == 0) { //是在 0 0 位置 那麼是一種跳法 if (x == 0 && y == 0) { return 1; } else { //反之此跳法不得行 return 0; } } return //假如當前位置(6,6)依賴於(5,8)(7,8),(8,7),(8,5)(5,4),(4,5),(4,7) recursion(x - 1, y + 2, step - 1) + recursion(x + 1, y + 2, step - 1) + recursion(x + 2, y + 1, step - 1) + recursion(x + 2, y - 1, step - 1) + recursion(x + 1, y - 2, step - 1) + recursion(x - 1, y - 2, step - 1) + recursion(x - 2, y - 1, step - 1) + recursion(x - 2, y + 1, step - 1) ; } /** * 檢查馬兒當前位置是否越界 跳出棋盤外 * * @param x 橫座標 * @param y 縱座標 * @return 是否越界 越界返回false */ private static boolean checkPosition(int x, int y) { return x >= 0 && x <= 8 && y >= 0 && y <= 9; } -
動態規劃
-
使用遞迴到動態規劃的套路
-
看遞迴方法可變引數的個數,這個可變引數的個數決定了dp陣列的大小和維度
可變引數三個 所以三維陣列,大小是棋盤的大小,第三維大小是step+1 -
看呼叫遞迴的方法的入參,可以知道我們的最終目的是dp中的哪一項
recursion(x, y, step);所以返回dp[x][y][step] -
根據遞迴的baseCase初始化dp陣列
//如果越界那麼說明當前遞迴樹的分支不得行 if (!checkPosition(x, y)) { return 0; } //意味著如果我們取dp陣列中的值越界了返回0//如果步數用完了 if (step == 0) { //是在 0 0 位置 那麼是一種跳法 if (x == 0 && y == 0) { return 1; } else { //反之此跳法不得行 return 0; } } //意味著 dp[0][0][0]初始化為1 其餘的點為0【因為我們起點定為了0】 -
根據遞迴中當前方法棧的返回值依賴於哪些遞迴的返回值,根據這個我們可以得到狀態轉移方程,
recursion(x - 1, y + 2, step - 1) + recursion(x + 1, y + 2, step - 1) + recursion(x + 2, y + 1, step - 1) + recursion(x + 2, y - 1, step - 1) + recursion(x + 1, y - 2, step - 1) + recursion(x - 1, y - 2, step - 1) + recursion(x - 2, y - 1, step - 1) + recursion(x - 2, y + 1, step - 1) //step看作z軸,當前層的值只依賴於下面層值 //dp[x][y][step]= // dp[x - 1][ y + 2]+[step - 1] //+ dp[x + 1][ y + 2]+[step - 1] //.....需要注意越界返回0這點 -
根據當前位置依賴於哪些位置,可以知道動態規劃for迴圈怎麼寫,從上到下,還是從下到上,從左到右還是從右到左
//dp[x][y][step]= // dp[x - 1][ y + 2]+[step - 1] //+ dp[x + 1][ y + 2]+[step - 1] //說明從低層到高層,x y並無講究
/** * 檢查馬兒當前位置是否越界 跳出棋盤外 * * @param x 橫座標 * @param y 縱座標 * @return 是否越界 越界返回false */ private static boolean checkPosition(int x, int y) { return x >= 0 && x <= 8 && y >= 0 && y <= 9; } static class DynamicProgramming { static int getValueOfDpArrayOutBoundReturn0(int[][][] dp, int x, int y, int step) { try { return dp[x][y][step]; } catch (Exception e) { return 0; } } static int horseJumpToTargetPosition(int x, int y, int step) { //目標位置太離譜。需要花完的步數不符合實際 返回0 if (!checkPosition(x, y) || step < 0) { return 0; } int[][][] dp = new int[8 + 1][9 + 1][step + 1]; dp[0][0][0] = 1; for (int curLayer = 1; curLayer <= step; curLayer++) { for (int curX = 0; curX <= 8; curX++) { for (int curY = 0; curY <= 9; curY++) { ///假如當前位置(6,6)依賴於(5,8)(7,8),(8,7),(8,5)(5,4),(4,5),(4,7) //curLayer=6 表示6步到(6,6) 右多少種方法, //方法總數等於 用五步到5,8)(7,8),(8,7),(8,5)(5,4),(4,5),(4,7)存在多少種方法 dp[curX][curY][curLayer] = getValueOfDpArrayOutBoundReturn0(dp, curX - 1, curY + 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 1, curY + 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 2, curY + 1, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 2, curY - 1, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX + 1, curY - 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX - 1, curY - 2, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX - 2, curY - 1, curLayer - 1) + getValueOfDpArrayOutBoundReturn0(dp, curX - 2, curY + 1, curLayer - 1); } } } return dp[x][y][step]; } } -
-
五丶leetcode上的一些動態規劃題目
這裡就沒一步步使用套路來,熟練了就直接可以想到狀態轉移方程,直接寫就完事了
1.[最長迴文子串](5. 最長迴文子串 - 力扣(Leetcode))
public String longestPalindrome(String s) {
if (s == null || s.length() <= 1) {
return s;
}
int len = s.length();
int maxLen = 1;
int begin = 0;
//dp[i][j] 表示 s[i..j] 是否是迴文串
boolean[][] dp = new boolean[len][len];
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
//i=1 j = 3 中間只有一個字元的時候,如果s[i]=s[j]那麼必然迴文
//dp[i][j] = s[i]==s[j] 且 dp[i+1][j-1]
//也就是說 當前格子依賴於左下方格子,那麼填格子使用一列一列的填
for (int j = 1; j < len; j++) {
//當前是第j列,第 i行 判斷是否迴文
for (int i = 0; i < j; i++) {
boolean charEqual = s.charAt(i) == s.charAt(j);
//dp[3][6] = s[3]==s[6] && dp[4][5];
if (j - i >= 3) {
dp[i][j] = charEqual && dp[i + 1][j - 1];
} else {
//j - i<3 說明中間只有一個 或者 0 個字元 那麼直接看s[i],s[j]是否相等
dp[i][j] = charEqual;
}
if (dp[i][j] && maxLen < j - i + 1) {
begin = i;
maxLen = j - i + 1;
}
}
}
return s.substring(begin, begin + maxLen);
}
2.[最大子陣列和](53. 最大子陣列和 - 力扣(Leetcode))
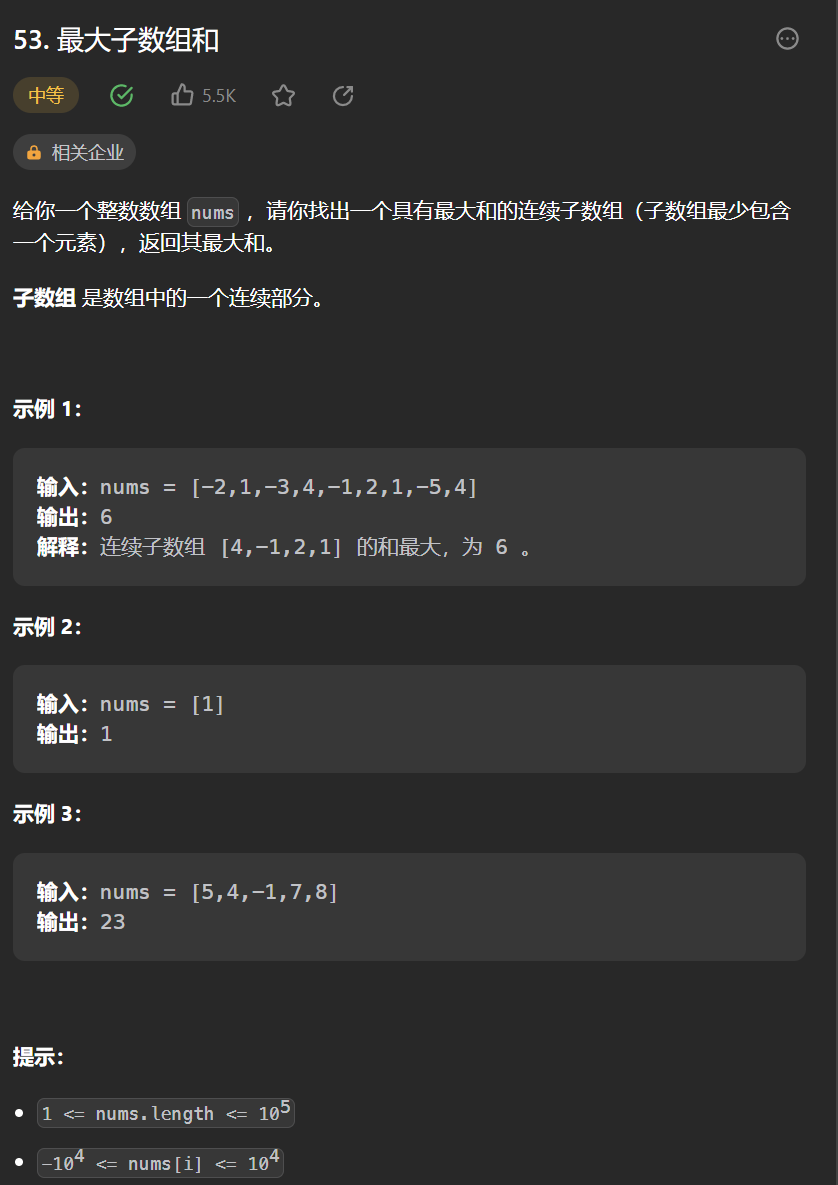
public int maxSubArray1(int[] nums) {
int maxSum = nums[0];
int len = nums.length;
//dp[i] dp[0....i]之間的每一個子陣列的,最大子陣列和
//dp[i] = max(dp[i-1],dp[i]+nums[i])
int[] dp = new int[len];
dp[0] = nums[0];
for(int i=1; i<len; i++){
dp[i] = Math.max(nums[i]+dp[i-1],nums[i]);
maxSum = Math.max(maxSum,dp[i]);
}
return maxSum;
}
public int maxSubArray(int[] nums) {
int maxSum = nums[0];
int len = nums.length;
int dp = nums[0];
for(int i=1; i<len; i++){
dp = Math.max(nums[i]+dp,nums[i]);
maxSum = Math.max(maxSum,dp);
}
return maxSum;
}
3.[跳躍遊戲](55. 跳躍遊戲 - 力扣(Leetcode))
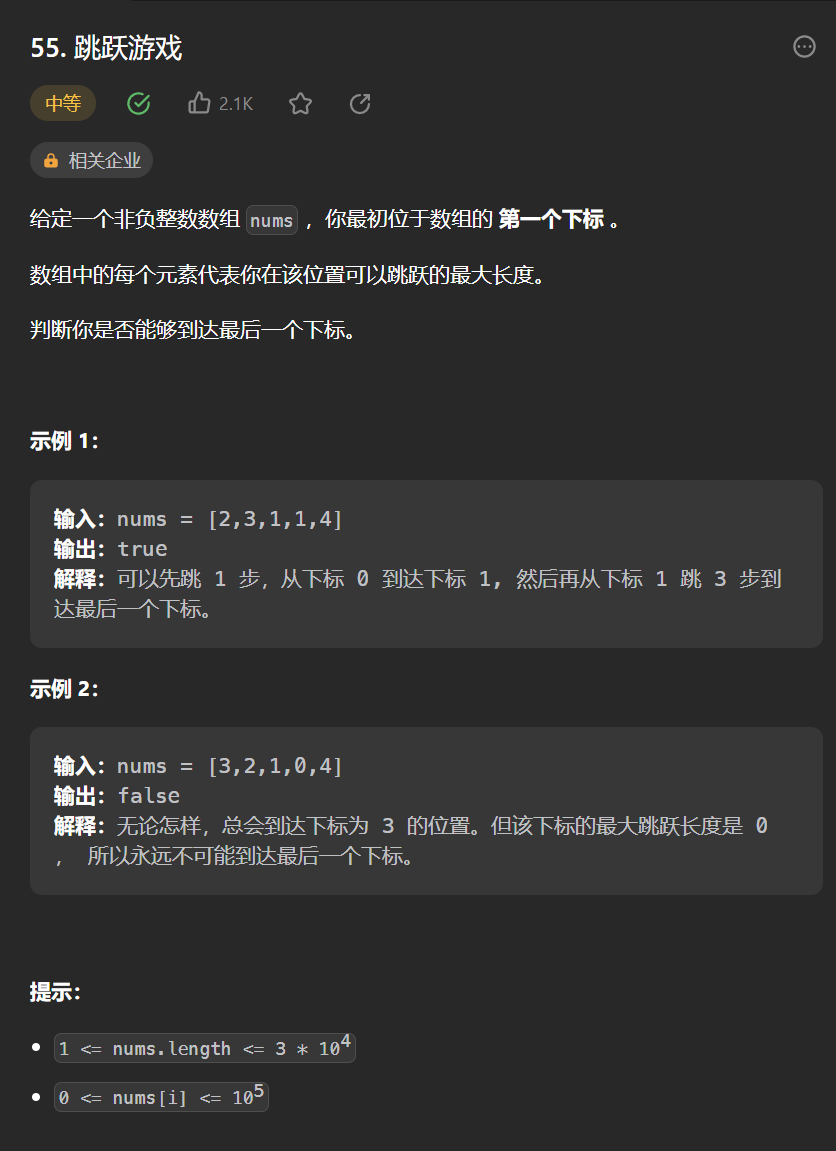
public boolean canJump(int[] nums) {
if(nums.length <=1){
return true;
}
//dp[i]表示能否跳到i位置
boolean[] dp = new boolean[nums.length];
dp[0]=true;
dp[1] = dp[0]&&nums[0]>=1;
//當前判斷是否可以跳到第i位置
for(int i =2 ;i < nums.length ; i++){
//i位置之前的所有位置遍歷判斷
//能否從pos 跳到 i位置
for(int pos=0;pos<i;pos++){
//首先如果連pos位置都沒辦法到達 那麼gg 進行下一輪迴圈
boolean canBePos = dp[pos];
if(!canBePos){
continue;
}
//pos 和i 的距離
int dis = i-pos;
//pos 位置能跳的最大距離是否大於 pos和i的距離
boolean jumpLenBetterDis = nums[pos]>=dis;
//如果可以 那麼說明i位置可以到達
if(jumpLenBetterDis){
dp[i]=true;
break;
}
}
}
return dp[nums.length-1];
}
4.[跳躍遊戲 II](45. 跳躍遊戲 II - 力扣(Leetcode))
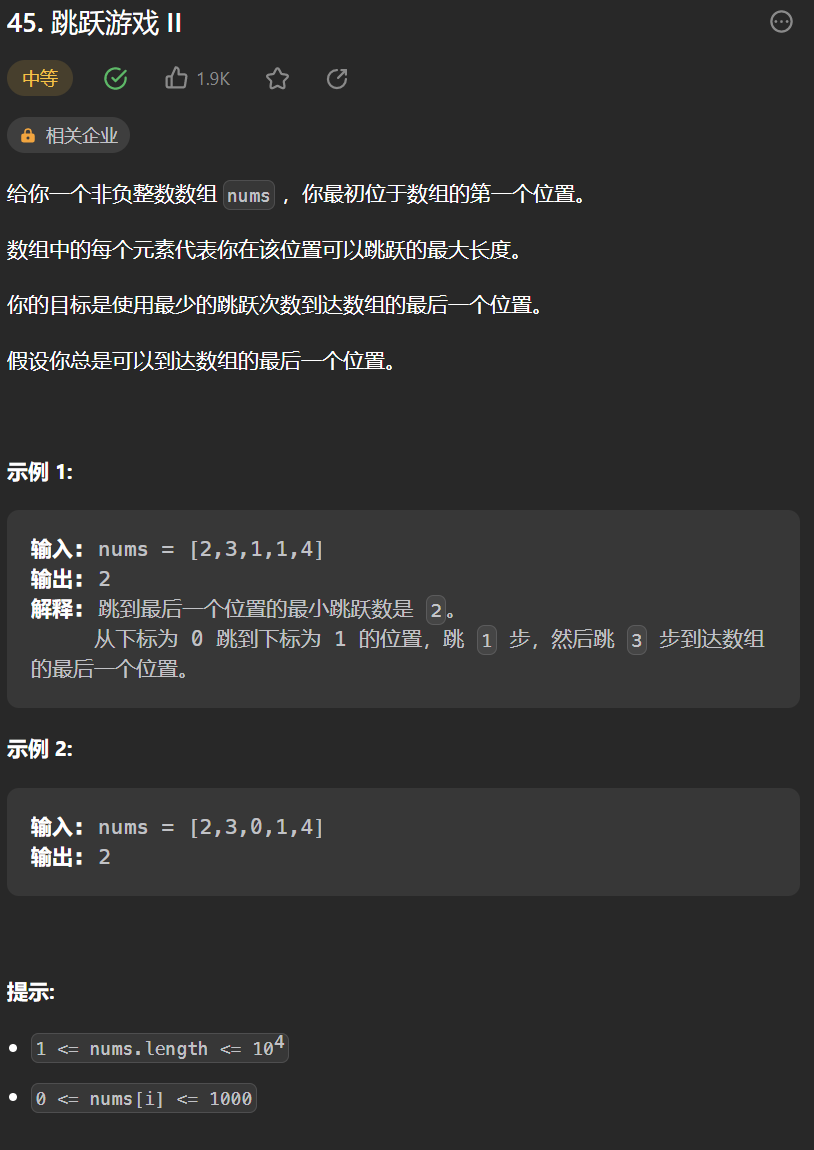
class Solution {
public int jump(int[] nums) {
if(nums.length<=1){
return 0;
}
int len = nums.length;
//dp[i]跳到i位置所需要的最西澳部署
int[]dp = new int[nums.length];
dp[0]=0;
dp[1]=1;
//跳到i位置最少的步數
for(int i = 2; i<len; i++){
//從pos 能否跳到i 如果可以那麼dp[i] = min(dp[i],dp[pos]+1)
for(int pos = 0;pos<i;pos++){
int maxCanJump = nums[pos];
//可以跳到
if(maxCanJump+pos>=i){
//dp[i]還沒有重新整理過 那麼 直接賦值
if(dp[i] == 0){
dp[i] = dp[pos]+1;
}else{
//取最小
dp[i] = Math.min(dp[pos]+1,dp[i]);
}
}
}
}
return dp[len-1];
}
}
5.[不同路徑](62. 不同路徑 - 力扣(Leetcode))
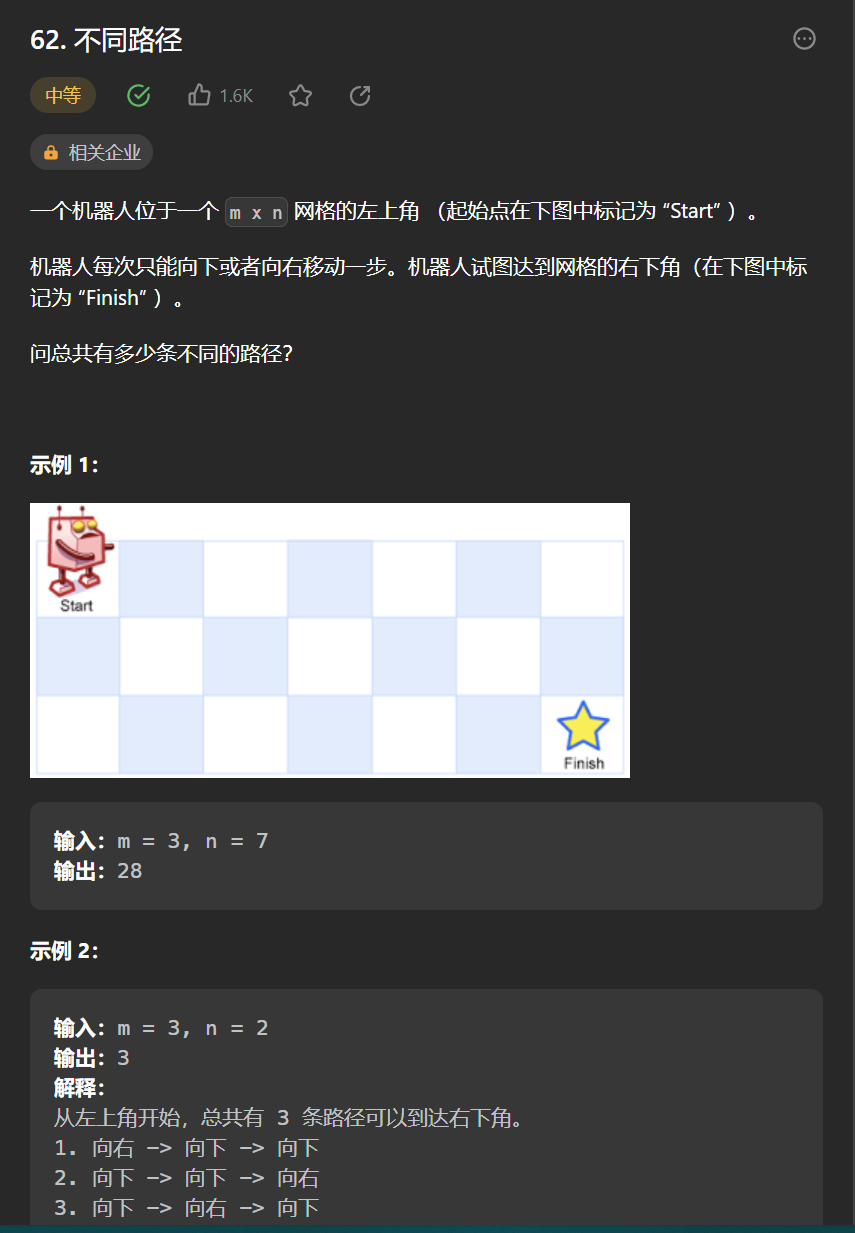
class Solution {
public int uniquePaths(int m, int n) {
if(m==1 && n==1){
return 1;
}
//dp[i][j] 表示到i,j位置有多少種走法
//dp[i][j] = dp[i-1][j] dp[i][j-1]
int[][] dp = new int[m][n];
dp[0][0] = 1;
for(int i=0; i<m ;i++){
for(int j=0;j<n;j++){
dp[i][j] += outBoudGet(dp,i-1,j);
dp[i][j] += outBoudGet(dp,i,j-1);
}
}
return dp[m-1][n-1];
}
int outBoudGet(int[][]dp,int i,int j ){
try{
return dp[i][j];
}catch(Exception e){
return 0;
}
}
}
6.[不同路徑 II](63. 不同路徑 II - 力扣(Leetcode))
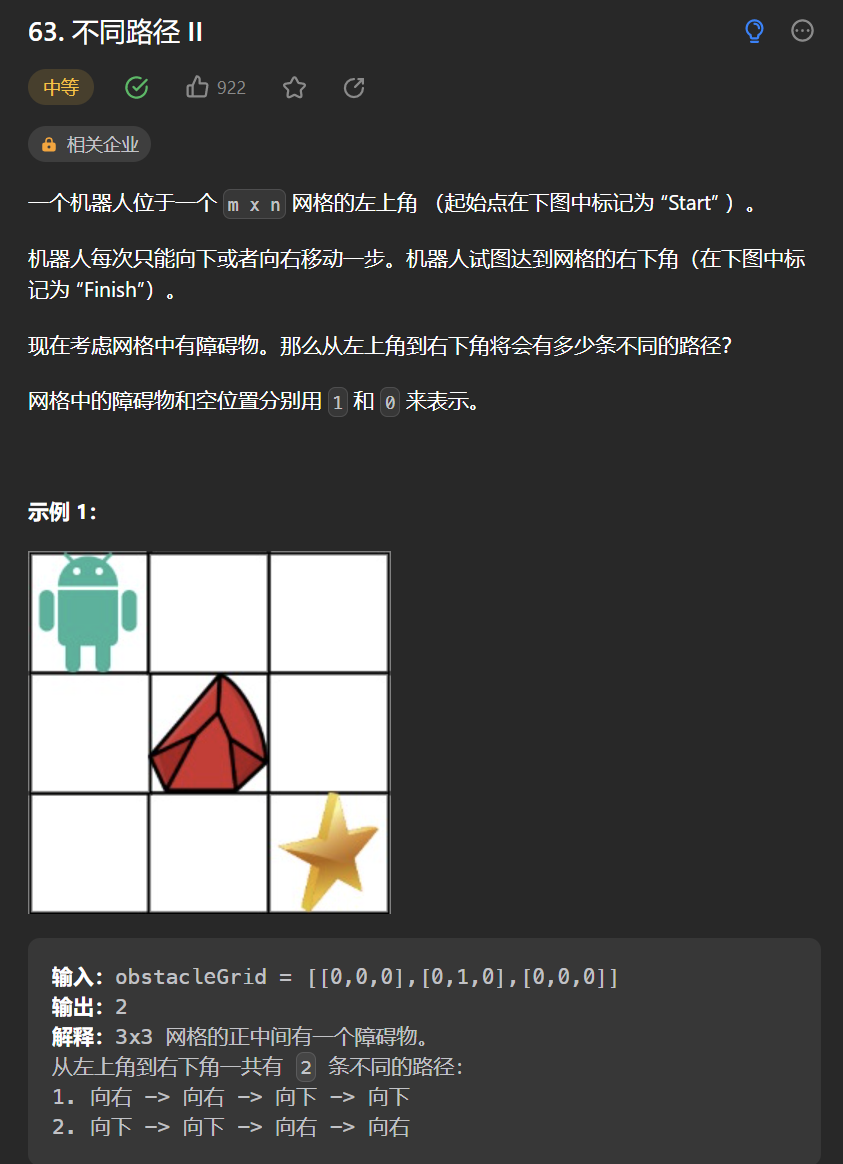
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
if (obstacleGrid[m - 1][n - 1] == 1) {
return 0;
}
//dp[i][j] 表示到i,j位置有多少種走法
//dp[i][j] = dp[i-1][j] dp[i][j-1]
int[][] dp = new int[m][n];
dp[0][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] += outBoudGet(dp, i - 1, j, obstacleGrid);
dp[i][j] += outBoudGet(dp, i, j - 1, obstacleGrid);
}
}
return dp[m - 1][n - 1];
}
int outBoudGet(int[][] dp, int i, int j, int[][] obstacleGrid) {
try {
if (obstacleGrid[i][j] == 1) {
return 0;
}
return dp[i][j];
} catch (Exception e) {
return 0;
}
}
}
7.[最小路徑和](64. 最小路徑和 - 力扣(Leetcode))

class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
//dp[i][j]表示走到i,j位置最小的路徑和
int[][]dp = new int[m][n];
dp[0][0] = grid[0][0];
for(int i = 0;i<m;i++){
for(int j = 0;j<n;j++){
int rowMinus = Integer.MAX_VALUE;
int colMinus = Integer.MAX_VALUE;
if(i-1>=0){
rowMinus = dp[i-1][j];
}
if(j-1>=0){
colMinus = dp[i][j-1];
}
int min = Math.min(rowMinus,colMinus);
if(min == Integer.MAX_VALUE){
min = 0;
}
dp[i][j] = min + grid[i][j];
}
}
return dp[m-1][n-1];
}
}
8.[買賣股票的最佳時機 II](122. 買賣股票的最佳時機 II - 力扣(Leetcode))
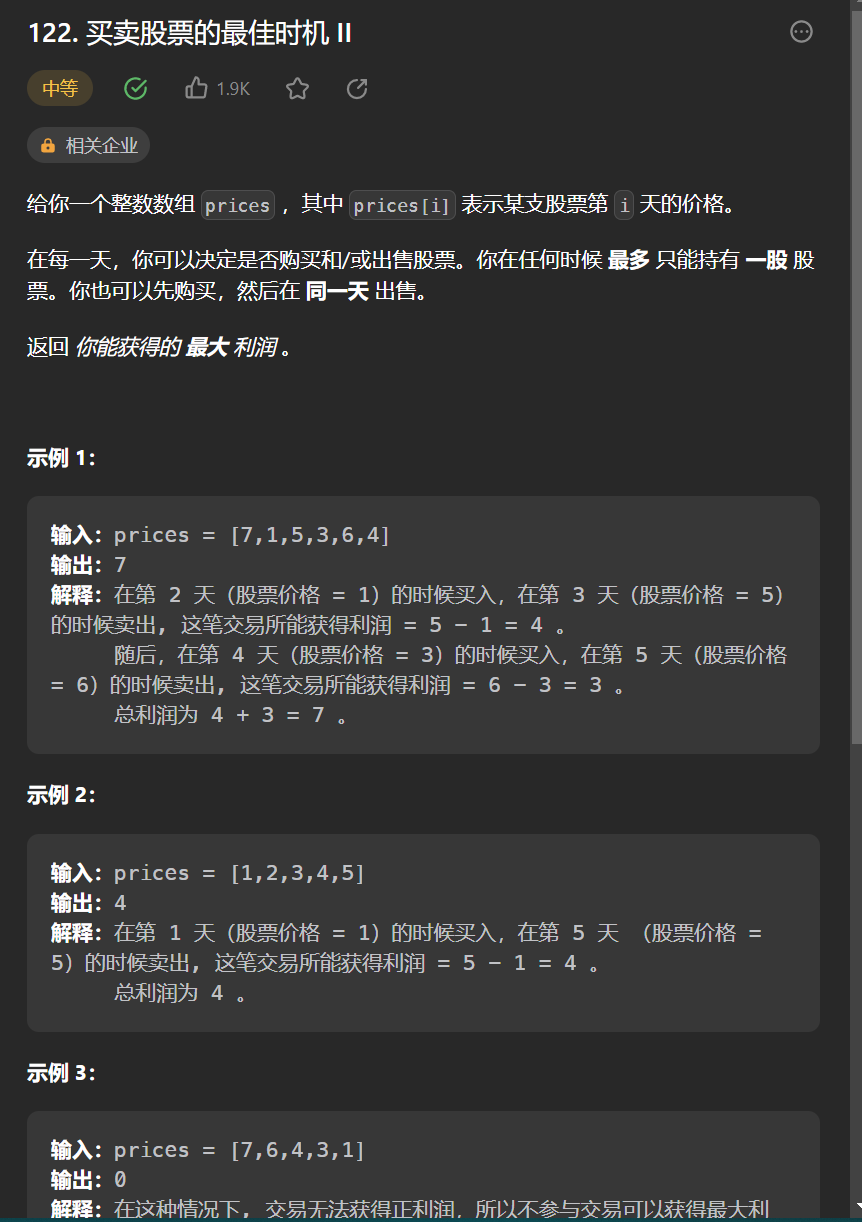
class Solution {
public int maxProfit1(int[] prices) {
int len = prices.length;
if(len<=1){
return 0;
}
//dp[i][0]表示第i+1天不持有股票的收益
//dp[i][1] 表示第i+1天持有當前股票的收益
int [][]dp = new int[len][2];
//第1天 不持有的股票收益,沒有機會買,也沒股票賣所有為0
dp[0][0] = 0;
//第1天 持有,都沒機會賣 那麼買入導致收益為負數
dp[0][1] = -prices[0];
//第二天開始
for (int i = 1; i < len; i++) {
//第二天不持有 那麼是第一天買然後賣賺 還是 繼續持有不買賺
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
//第二天持有,那麼是第一天的繼續持有賺,還是前一天不買,現在買賺
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[len - 1][0];
}
public int maxProfit(int[] prices) {
int len = prices.length;
if(len<=1){
return 0;
}
//第1天 不持有的股票收益,沒有機會買,也沒股票賣所有為0
int dpNotHold = 0;
//第1天 持有,都沒機會賣 那麼買入導致收益為負數
int dpHold = -prices[0];
//第二天開始
for (int i = 1; i < len; ++i) {
//第二天不持有 那麼是第一天買然後賣賺 還是 繼續持有不買賺
int dpNotHoldNew = Math.max(dpNotHold, dpHold + prices[i]);
//第二天持有,那麼是第一天的繼續持有賺,還是前一天不買,現在買賺
int dpHoldNew = Math.max(dpHold, dpNotHold - prices[i]);
dpNotHold = dpNotHoldNew;
dpHold = dpHoldNew;
}
return dpNotHold;
}
}
9.[單詞拆分](139. 單詞拆分 - 力扣(Leetcode))
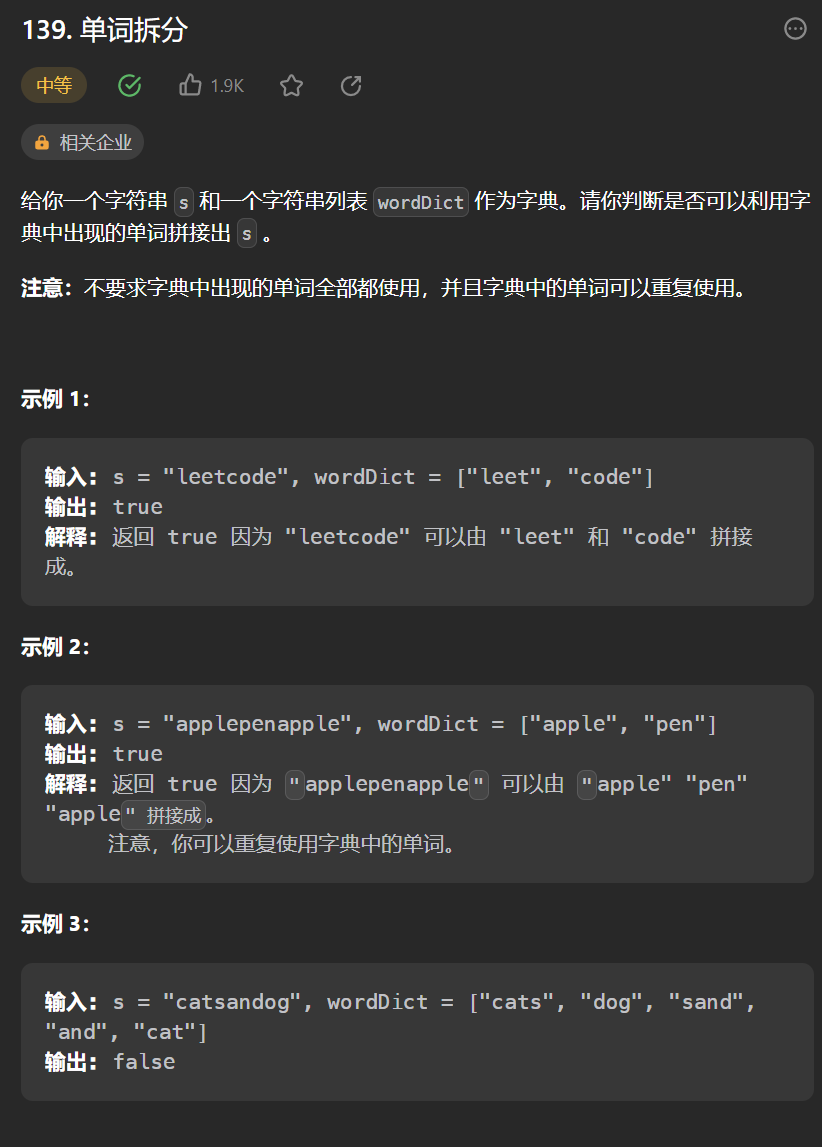
class Solution {
public int maxProduct1(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i結尾的子陣列最大值
//dp[i][1]則表示最小值
int[][] dp = new int[len][2];
//初始化自己一個人作為子陣列的值
for(int i = 0 ; i < len ; i++){
dp[i][0] = nums[i];
dp[i][1] = nums[i];
}
int maxRes = dp[0][0];
for(int i = 1 ; i < len ; i++){
//以i結尾
int max = Math.max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]);
//和 單獨作為子陣列取最大
max = Math.max(max,dp[i][0]);
dp[i][0] = max;
maxRes = Math.max(max,maxRes);
int min = Math.min(dp[i-1][1]*nums[i],dp[i-1][0]*nums[i]);
min = Math.min(min,dp[i][1]);
dp[i][1] = min;
}
return maxRes;
}
public int maxProduct(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i結尾的子陣列最大值
//dp[i][1]則表示最小值
int maxPre = nums[0];
int minPre = nums[0];
int maxRes = maxPre;
for(int i = 1 ; i < len ; i++){
//以i結尾
int max = Math.max(maxPre*nums[i],minPre*nums[i]);
//和 單獨作為子陣列取最大
max = Math.max(max,nums[i]);
int min = Math.min(minPre*nums[i],maxPre*nums[i]);
min = Math.min(min,nums[i]);
maxPre = max;
minPre = min;
maxRes = Math.max(max,maxRes);
}
return maxRes;
}
}
152.[乘積最大子陣列](152. 乘積最大子陣列 - 力扣(Leetcode))
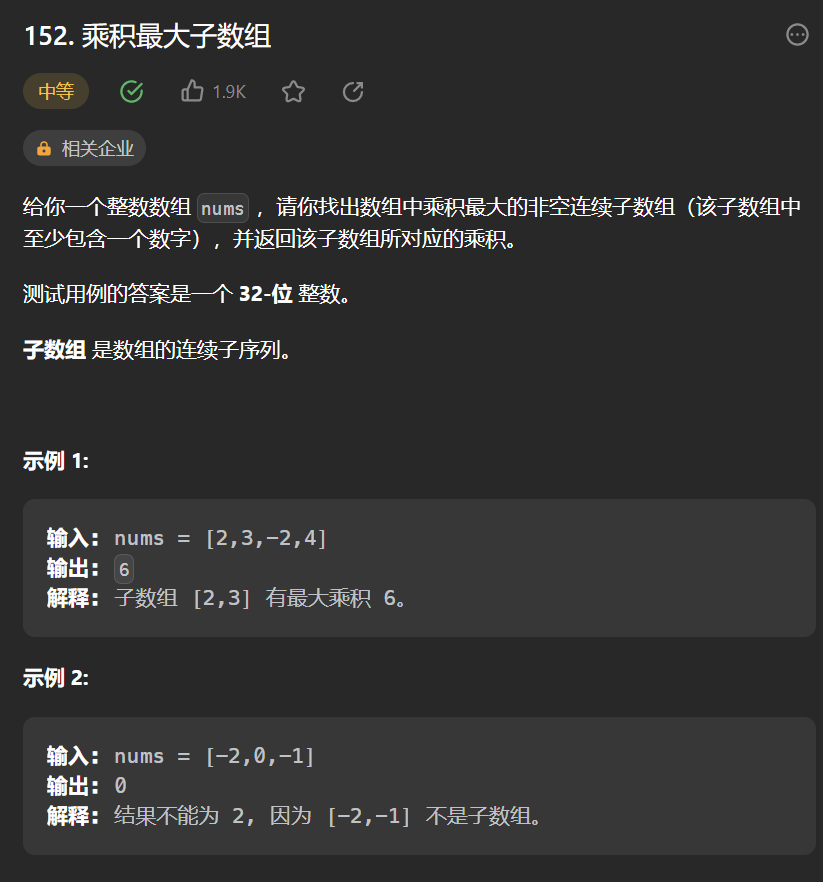
class Solution {
public int maxProduct1(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i結尾的子陣列最大值
//dp[i][1]則表示最小值
int[][] dp = new int[len][2];
//初始化自己一個人作為子陣列的值
for(int i = 0 ; i < len ; i++){
dp[i][0] = nums[i];
dp[i][1] = nums[i];
}
int maxRes = dp[0][0];
for(int i = 1 ; i < len ; i++){
//以i結尾
int max = Math.max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]);
//和 單獨作為子陣列取最大
max = Math.max(max,dp[i][0]);
dp[i][0] = max;
maxRes = Math.max(max,maxRes);
int min = Math.min(dp[i-1][1]*nums[i],dp[i-1][0]*nums[i]);
min = Math.min(min,dp[i][1]);
dp[i][1] = min;
}
return maxRes;
}
public int maxProduct(int[] nums) {
int len = nums.length ;
//dp[i][0]表示 以i結尾的子陣列最大值
//dp[i][1]則表示最小值
int maxPre = nums[0];
int minPre = nums[0];
int maxRes = maxPre;
for(int i = 1 ; i < len ; i++){
//以i結尾
int max = Math.max(maxPre*nums[i],minPre*nums[i]);
//和 單獨作為子陣列取最大
max = Math.max(max,nums[i]);
int min = Math.min(minPre*nums[i],maxPre*nums[i]);
min = Math.min(min,nums[i]);
maxPre = max;
minPre = min;
maxRes = Math.max(max,maxRes);
}
return maxRes;
}
}