技術文章 » 神經網路模型量化基礎

神經網路模型量化基礎

2022-12-04 06:00:32

本文為對目前線性量化優點、原理、方法和實戰內容的總結，主要參考 神經網路量化簡介 並加以自己的理解和總結，適合初學者閱讀和自身複習用。

1，模型量化概述

1.1，模型量化優點

模型量化是指將神經網路的浮點演演算法轉換為定點。量化有一些相似的術語，低精度（Low precision）可能是常見的。

  • 低精度模型表示模型權重數值格式為 FP16（半精度浮點）或者 INT8（8位元的定點整數），但是目前低精度往往就指代 INT8。
  • 常規精度模型則一般表示模型權重數值格式為 FP32（32位元浮點，單精度）。
  • 混合精度（Mixed precision）則在模型中同時使用 FP32 和 FP16 的權重數值格式。 FP16 減少了一半的記憶體大小，但有些引數或操作符必須採用 FP32 格式才能保持準確度。

模型量化有以下好處：

參考 TensorFlow 模型優化：模型量化-張益新

  • 減小模型大小：如 int8 量化可減少 75% 的模型大小，int8 量化模型大小一般為 32 位浮點模型大小的 1/4：
    • 減少儲存空間：在端側儲存空間不足時更具備意義。
    • 減少記憶體佔用：更小的模型當然就意味著不需要更多的記憶體空間。
    • 減少裝置功耗：記憶體耗用少了推理速度快了自然減少了裝置功耗；
  • 加快推理速度，存取一次 32 位浮點型可以存取四次 int8 整型，整型運算比浮點型運算更快；CPU 用 int8 計算的速度更快
  • 某些硬體加速器如 DSP/NPU 只支援 int8。比如有些微處理器屬於 8 位的，低功耗執行浮點運算速度慢，需要進行 8bit 量化。

總結：模型量化主要意義就是加快模型端側的推理速度，並降低裝置功耗和減少儲存空間，

工業界一般只使用 INT8 量化模型，如 NCNN、TNN 等行動端模型推理框架都支援模型的 INT8 量化和量化模型的推理功能。

通常，可以根據 FP32 和 INT8 的轉換機制對量化模型推理方案進行分類。一些框架簡單地引入了 Quantize 和 Dequantize 層，當從折積或全連結層送入或取出時，它將 FP32 轉換為 INT8 或相反。在這種情況下，如下圖的上半部分所示，模型本身和輸入/輸出採用 FP32 格式。深度學習推理框架載入模型時，重寫網路以插入 Quantize 和 Dequantize 層，並將權重轉換為 INT8 格式。

注意，之所以要插入反量化層（Dequantize），是因為量化技術的早期，只有折積運算元支援量化，但實際網路中還包含其他運算元，而其他運算元又只支援 FP32 計算，因此需要把 INT8 轉換成 FP32。但隨著技術的迭代，後期估計會逐步改善乃至消除 Dequantize 操作，達成全網路的量化執行，而不是部分運算元量化執行。

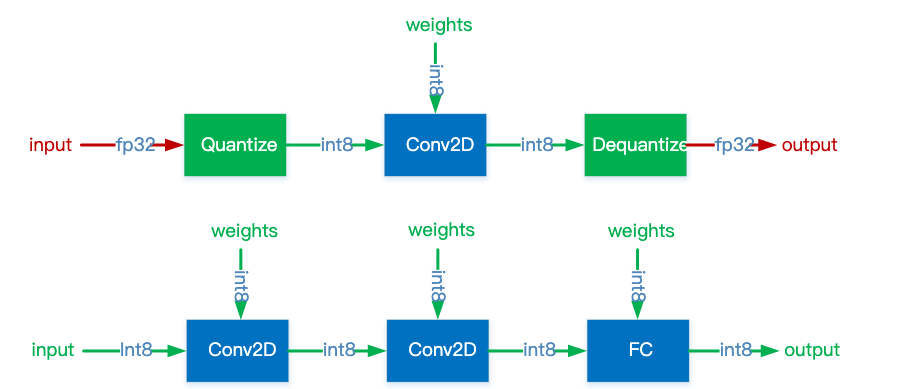
圖四：混合 FP32/INT8 和純 INT8 推理。紅色為 FP32，綠色為 INT8 或量化。

其他一些框架將網路整體轉換為 INT8 格式，因此在推理期間沒有格式轉換，如上圖的下半部分。該方法要求運算元（Operator）都支援量化，因為運運算元之間的資料流是 INT8。對於尚未支援的那些，它可能會回落到 Quantize/Dequantize 方案。

1.2，模型量化的方案

在實踐中將浮點模型轉為量化模型的方法有以下三種方法：

  1. data free：不使用校準集，傳統的方法直接將浮點引數轉化成量化數，使用上非常簡單，但是一般會帶來很大的精度損失，但是高通最新的論文 DFQ 不使用校準集也得到了很高的精度。
  2. calibration：基於校準集方案，通過輸入少量真實資料進行統計分析。很多晶片廠商都提供這樣的功能，如 tensorRT、高通、海思、地平線、寒武紀
  3. finetune：基於訓練 finetune 的方案，將量化誤差在訓練時模擬建模，調整權重使其更適合量化。好處是能帶來更大的精度提升，缺點是要修改模型訓練程式碼，開發週期較長。

TensorFlow 框架按照量化階段的不同，其模型量化功能分為以下兩種：

  • Post-training quantization PTQ（訓練後量化、離線量化）；
  • Quantization-aware training QAT（訓練時量化，偽量化，線上量化）。

1.2.1，PTQ 理解

PTQ Post Training Quantization 是訓練後量化，也叫做離線量化，根據量化零點 \(x_{zero\_point}\) 是否為 0，訓練後量化分為對稱量化和非對稱量化；根據資料通道順序 NHWC(TensorFlow) 這一維度區分，訓練後量化又分為逐層量化和逐通道量化。目前 nvidia 的 TensorRT 框架中使用了逐層量化的方法，每一層採用同一個閾值來進行量化。逐通道量化就是對每一層每個通道都有各自的閾值，對精度可以有一個很好的提升。

1.3，量化的分類

目前已知的加快推理速度概率較大的量化方法主要有：

  1. 二值化，其可以用簡單的位運算來同時計算大量的數。對比從 nvdia gpu 到 x86 平臺，1bit 計算分別有 5 到128倍的理論效能提升。且其只會引入一個額外的量化操作，該操作可以享受到 SIMD（單指令多資料流）的加速收益。
  2. 線性量化(最常見)，又可細分為非對稱，對稱和 ristretto 幾種。在 nvdia gpu，x86、arm 和 部分 AI 晶片平臺上，均支援 8bit 的計算，效率提升從 1 倍到 16 倍不等，其中 tensor core 甚至支援 4bit計算，這也是非常有潛力的方向。線性量化引入的額外量化/反量化計算都是標準的向量操作，因此也可以使用 SIMD 進行加速，帶來的額外計算耗時不大。
  3. 對數量化，一種比較特殊的量化方法。兩個同底的冪指數進行相乘，那麼等價於其指數相加，降低了計算強度。同時加法也被轉變為索引計算。目前 nvdia gpu，x86、arm 三大平臺上沒有實現對數量化的加速庫，但是目前已知海思 351X 系列晶片上使用了對數量化。

1.3.1，線性量化概述

與非線性量化不同，線性量化採用均勻分佈的聚類中心，原始浮點資料和量化後的定點資料存在一個簡單的線性變換關係，因為折積、全連線等網路層本身只是簡單的線性計算，因此線性量化中可以直接用量化後的資料進行直接計算。

2，量化算術

模型量化過程可以分為兩部分：將模型從 FP32 轉換為 INT8，以及使用 INT8 進行推理。本節說明這兩部分背後的算術原理。如果不瞭解基礎算術原理，在考慮量化細節時通常會感到困惑。

2.1，定點和浮點

定點和浮點都是數值的表示（representation），它們區別在於，將整數（integer）部分和小數（fractional）部分分開的點，點在哪裡。定點保留特定位數整數和小數，而浮點保留特定位數的有效數位（significand）和指數（exponent）。

絕大多數現代的計算機系統採納了浮點數表示方式，這種表達方式利用科學計數法來表達實數。即用一個尾數(Mantissa，尾數有時也稱為有效數位，它實際上是有效數位的非正式說法)，一個基數(Base)，一個指數(Exponent)以及一個表示正負的符號來表達實數。具體組成如下：

  • 第一部分為 sign 符號位 \(s\)，佔 1 bit，用來表示正負號；
  • 第二部分為 exponent 指數偏移值 \(k\)，佔 8 bits，用來表示其是 2 的多少次冪；
  • 第三部分是 fraction 分數值（有效數位） \(M\)，佔 23 bits，用來表示該浮點數的數值大小。

基於上述表示，浮點數的值可以用以下公式計算：

\[(-1)^s \times M \times 2^k \]

值得注意是，上述公式隱藏了一些細節，如指數偏移值 \(k\) 使用的時候需要加上一個固定的偏移值。

比如 123.45 用十進位制科學計數法可以表示為 \(1.2345\times 10^2\)，其中 1.2345 為尾數，10 為基數，2 為指數。

單精度浮點型別 float 佔用 32bit，所以也稱作 FP32；雙精度浮點型別 double 佔用 64bit。

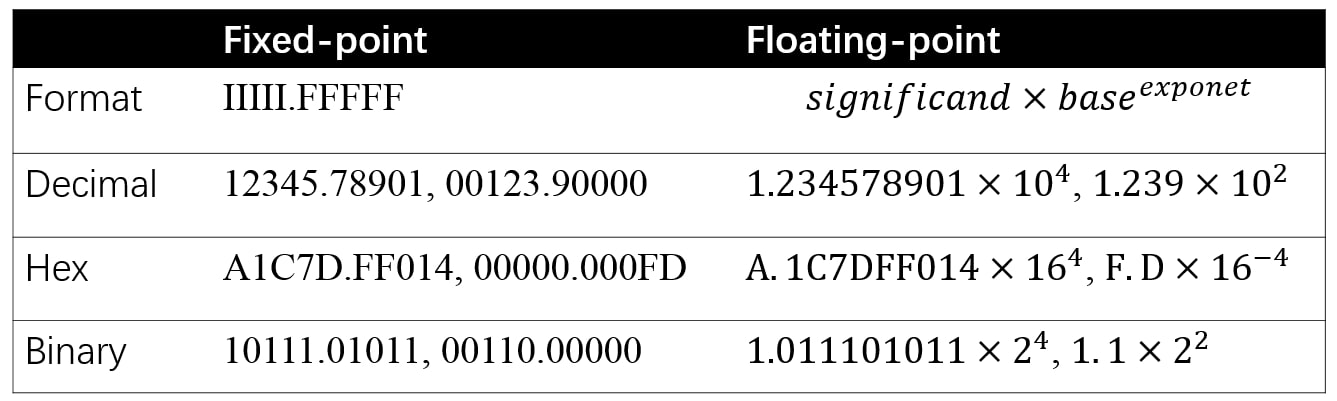
圖五：定點和浮點的格式和範例。

2.2，量化浮點

32-bit 浮點數和 8-bit 定點數的表示範圍如下表所示：

資料型別 最小值 最大值
FP32 -3.4e38 3.4e38
int8 -128 128
uint8 0 255

神經網路的推理由浮點運算構成。FP32 和 INT8 的值域是 \([(2−2^{23})×2^{127},(2^{23}−2)\times 2^{127}]\) 和 \([−128,127]\)，而取值數量大約分別為 \(2^{32}\) 和 \(2^8\) 。FP32 取值範圍非常廣，因此，將網路從 FP32 轉換為 INT8 並不像資料型別轉換截斷那樣簡單。但是，一般神經網路權重的值分佈範圍很窄，非常接近零。圖八給出了 MobileNetV1 中十層（擁有最多值的層）的權重分佈。

圖八：十層 MobileNetV1 的權重分佈。

根據偏移量 \(Z\) 是否為 0，可以將浮點數的線性量化分為兩類-對稱量化和非對稱量化。

當浮點值域落在 \((-1,1)\) 之間，權重浮點資料的量化運算可使用下式的方法將 FP32 對映到 INT8，這是對稱量化。其中 \(x_{float}\) 表示 FP32 權重， \(x_{quantized}\) 表示量化的 INT8 權重，\(x_{scale}\) 是縮放因子（對映因子、量化尺度（範圍）/ float32 的縮放因子）。

\[x_{float} = x_{scale} \times x_{quantized} \]

對稱量化的浮點值和 8 位定點值的對映關係如下圖，從圖中可以看出，對稱量化就是將一個 tensor 中的 \([-max(|\mathrm{x}|),max(|\mathrm{x}|)]\) 內的 FP32 值分別對映到 8 bit 資料的 [-128, 127] 的範圍內，中間值按照線性關係進行對映，稱這種對映關係是對稱量化。可以看出，對稱量化的浮點值和量化值範圍都是相對於零對稱的。

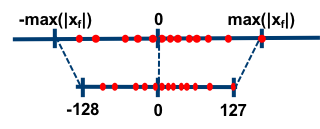
因為對稱量化的縮放方法可能會將 FP32 零對映到 INT8 零，但我們不希望這種情況出現，於是出現了數位訊號處理中的均一量化，即非對稱量化。數學表示式如下所示，其中 \(x_{zero\_point}\) 表示量化零點（量化偏移）。

\[x_{float} = x_{scale} \times (x_{quantized} - x_{zero\_point}) \]

大多數情況下量化是選用無符號整數，即 INT8 的值域就為 \([0,255]\) ，這種情況，顯然要用非對稱量化。非對稱量化的浮點值和 8 位定點值的對映關係如下圖：

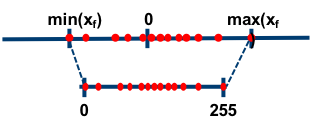
總的來說，權重量化浮點值可以分為兩個步驟：

  1. 通過在權重張量（Tensor）中找到 \(min\) 和 \(max\) 值從而確定 \(x_{scale}\) 和\(x_{zero\_point}\)。
  2. 將權重張量的每個值從 FP32 轉換為 INT8 。

\[\begin{align} x_{float} &\in [x_{float}^{min}, x_{float}^{max}] \\ x_{scale} &= \frac{x_{float}^{max} - x_{float}^{min}}{x_{quantized}^{max} - x_{quantized}^{min}} \\ x_{zero\_point} &= x_{quantized}^{max} - x_{float}^{max} \div x_{scale} \\ x_{quantized} &= x_{float} \div x_{scale} + x_{zero\_point} \end{align}\]

注意，當浮點運算結果不等於整數時，需要額外的舍入步驟。例如將 FP32 值域 [−1,1] 對映到 INT8 值域 [0,255]，有 \(x_{scale}=\frac{2}{255}\)，而\(x_{zero\_point}= 255−\frac{255}{2}≈127\)。

注意，量化過程中存在誤差是不可避免的，就像數位訊號處理中量化一樣。非對稱演演算法一般能夠較好地處理資料分佈不均勻的情況。

2.2，量化算術

量化的一個重要議題是用量化算術表示非量化算術，即量化神經網路中的 INT8 計算是描述常規神經網路的 FP32 計算，對應的就是反量化過程，也就是如何將 INT8 的定點資料反量化成 FP32 的浮點資料。

下面的等式 5-10 是反量化乘法 \(x_{float} \cdot y_{float}\) 的過程。對於給定神經網路，輸入 \(x\)、權重 \(y\) 和輸出 \(z\) 的縮放因子肯定是已知的，因此等式 14 的 \(Multiplier_{x,y,z} = \frac{x_{scale}y_{scale}}{z_{scale}}\) 也是已知的，在反量化過程之前可預先計算。因此，除了 \(Multiplier_{x,y,z}\) 和 \((x_{quantized} - x_{zero\_point})\cdot (y_{quantized} - y_{zero\_point})\) 之間的乘法外，等式 16 中的運算都是整數運算。

\[\begin{align} z_{float} & = x_{float} \cdot y_{float} \\ z_{scale} \cdot (z_{quantized} - z_{zero\_point}) & = (x_{scale} \cdot (x_{quantized} - x_{zero\_point})) \cdot (y_{scale} \cdot (y_{quantized} - y_{zero\_point})) \\ z_{quantized} - z_{zero\_point} &= \frac{x_{scale} \cdot y_{scale}}{z_{scale}} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) \\ z_{quantized} &= \frac{x_{scale} \cdot y_{scale}}{z_{scale}} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) + z_{zero\_point} \\ Multiplier_{x,y,z} &= \frac{x_{scale} \cdot y_{scale}}{z_{scale}} \\ z_{quantized} &= Multiplier_{x,y,z} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) + z_{zero\_point} \\ \end{align}\]

等式：反量化算術過程。

對於等式 10 可以應用的大多數情況，\(quantized\) 和 \(zero\_point\) 變數 (x,y) 都是 INT8 型別，\(scale\) 是 FP32。實際上兩個 INT8 之間的算術運算會累加到 INT16 或 INT32，這時 INT8 的值域可能無法儲存運算結果。例如，對於 \(x_{quantized}=20\)、\(x_{zero\_point} = 50\) 的情況，有 \((x_{quantized} − x_{zero_point}) = −30\) 超出 INT8 值範圍 \([0,255]\)。

資料型別轉換可能將 \(Multiplier_{x,y,z} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point})\) 轉換為 INT32 或 INT16，和 \(z_{zero\_point}\) 一起確保計算結果幾乎全部落入 INT8 值域 [0,255] 中。

對於以上情況，在工程中，比如對於折積運算元的計算，sum(x*y) 的結果需要用 INT32 儲存，同時，b 值一般也是 INT32 格式的，之後再 requantize (重新量化)成 INT8。

3，量化方法的改進

量化浮點部分中描述權重浮點量化方法是非常簡單的。在深度學習框架的早期開發中，這種簡單的方法能快速跑通 INT8 推理功能，然而採用這種方法的網路的預測準確度通常會出現明顯的下降。

雖然 FP32 權重的值域很窄，在這值域中數值點數量卻很大。以上文的縮放為例，\([−1,1]\) 值域中 \(2^{31}\)（是的，基本上是總得可表示數值的一半）個 FP32 值被對映到 \(256\) 個 INT8 值。

  • 量化型別：（SYMMETRIC） 對稱量化和 (NON-SYMMETRIC） 非對稱量化；
  • 量化演演算法：MINMAX、KL 散度、ADMM；
  • 權重量化型別：per-channel per-layer；

採用普通量化方法時，靠近零的浮點值在量化時沒有精確地用定點值表示。因此，與原始網路相比，量化網路一般會有明顯的精度損失。對於線性（均勻）量化，這個問題是不可避免的。

同時值對映的精度是受由 \(x_{float}^{min}\) 和 \(x_{float}^{max}\) 得到的 \(x_{scale}\) 顯著影響的。並且，如圖十所示，權重中鄰近 \(x_{float}^{min}\) 和 \(x_{float}^{max}\) 附近的值通常是可忽略的，其實就等同於對映關係中浮點值的 min 和 max 值是可以通過演演算法選擇的。

圖十將浮點量化為定點時調整最小值-最大值。

上圖展示了可以調整 min/max 來選擇一個值域，使得值域的值更準確地量化，而範圍外的值則直接對映到定點的 min/max。例如，當從原始值範圍 \([−1,1]\) 中選定\(x_{min}^{float} = −0.9\) 和 \(x_{max}^{float} = 0.8\) ，\([−0.9,0.8]\) 中的值將能更準確地對映到 \([0,255]\) 中，而 \([−1,−0.9]\) 和 \([0.8,1]\) 中的值分別對映為 \(0\) 和 \(255\)。

3.1，浮點數動態範圍選擇

參考乾貨：深度學習模型量化（低精度推理）大總結。

通過前文對量化算數的理解和上面兩種量化演演算法的介紹我們不難發現，為了計算 scale 和 zero_point，我們需要知道 FP32 weight/activation 的實際動態範圍。對於推理過程來說，weight 是一個常數張量，動態範圍是固定的，activation 的動態範圍是變化的，它的實際動態範圍必須經過取樣獲取（一般把這個過程稱為資料校準(calibration)）。

將浮點量化轉為定點時調整最小值/最大值（值域調整），也就是浮點數動態範圍的選擇，動態範圍的選取直接決定了量化資料的分佈情況，處於動態範圍之外的資料將被對映成量化資料的邊界點，即值域的選擇直接決定了量化的誤差。

目前各大深度學習框架和三大平臺的推理框架使用最多的有最大最小值（MinMax）、滑動平均最大最小值（MovingAverageMinMax）和 KL 距離（Kullback-Leibler divergence）三種方法，去確定浮點數的動態範圍。如果量化過程中的每一個 FP32 數值都在這個實際動態範圍內，我們一般稱這種為不飽和狀態；反之如果出現某些 FP32 數值不在這個實際動態範圍之內我們稱之為飽和狀態。

3.2，最大最小值（MinMax）

MinMax 是使用最簡單也是較為常用的一種取樣方法。基本思想是直接從 FP32 張量中選取最大值和最小值來確定實際的動態範圍，如下公式所示。
\(x_{min} = \left\{\begin{matrix}min(X) & if\ x_{min} = None \\ min(x_{min}, min(X)) & otherwise\end{matrix}\right.\)

\(x_{max} = \left\{\begin{matrix}max(X) & if\ x_{max} = None \\ max(x_{max}, max(X)) & otherwise\end{matrix}\right.\)

對 weights 而言，這種取樣方法是不飽和的，但是對於 activation 而言，如果取樣資料中出現離群點，則可能明顯擴大實際的動態範圍，比如實際計算時 99% 的資料都均勻分佈在 [-100, 100] 之間，但是在取樣時有一個離群點的數值為 10000，這時候取樣獲得的動態範圍就變成 [-100, 10000]。

3.3，滑動平均最大最小值(MovingAverageMinMax)

與 MinMax 演演算法直接替換不同，MovingAverageMinMax 會採用一個超引數 c (Pytorch 預設值為0.01)逐步更新動態範圍。
\(x_{min} = \left\{\begin{matrix}min(X) & if x_{min} = None \\ (1-c)x_{min}+c \; min(X) & otherwise\end{matrix}\right.\)

\(x_{max} = \left\{\begin{matrix}max(X) & if x_{max} = None \\ (1-c)x_{max}+c \; max(X) & otherwise\end{matrix}\right.\)
這種方法獲得的動態範圍一般要小於實際的動態範圍。對於 weights 而言，由於不存在取樣的迭代，因此 MovingAverageMinMax 與 MinMax 的效果是一樣的。

3.4，KL 距離取樣方法(Kullback–Leibler divergence)

理解 KL 散度方法之前，我們先看下 TensorRT 關於值域範圍閾值選擇的一張圖：

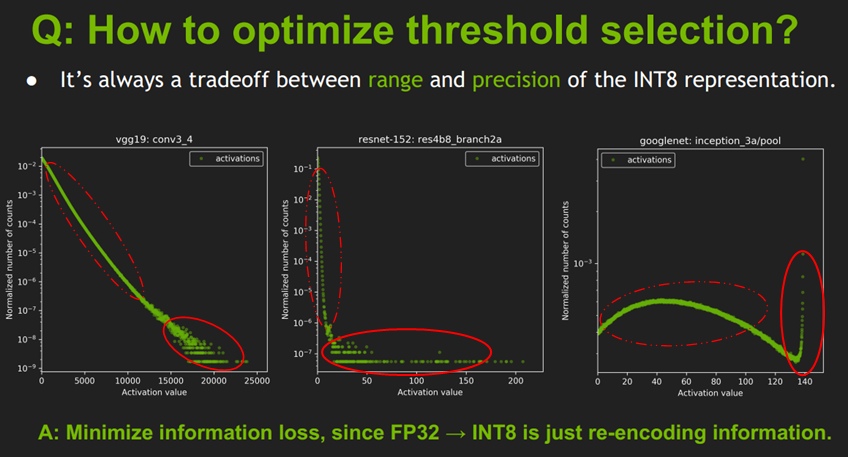
這張圖展示的是不同網路結構的不同 layer 的啟用值分佈統計圖，橫座標是啟用值，縱座標是統計數量的歸一化表示，而不是絕對數值統計；圖中有折積層和池化層，它們之間分佈很不相同，因此合理的量化方法應該是適用於不同的啟用值分佈，並且減小資訊損失，因為從 FP32 到 INT8 其實也是一種資訊再編碼的過程。

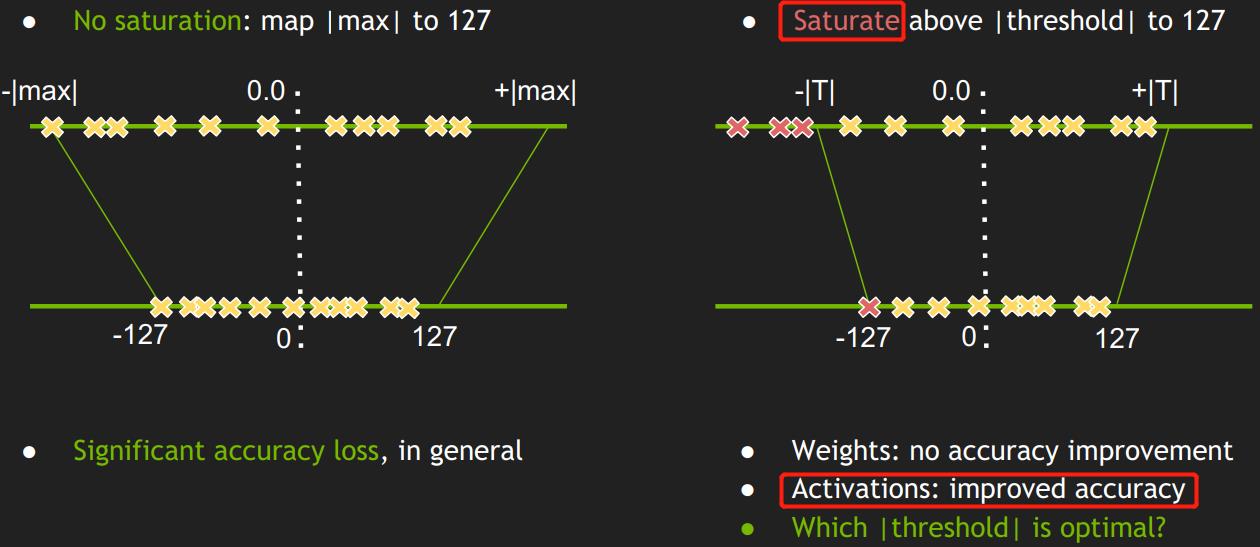
簡單的將一個 tensor 中的 -|max| 和 |max| FP32 value 對映為 -127 和 127 ，中間值按照線性關係進行對映，這種對映關係為不飽和的（No saturation），即對稱的。對於這種簡單的量化浮點方法，試驗結果顯示會導致比較大的精度損失。

通過上圖可以分析出，線性量化中使用簡單的量化浮點方法導致精度損失較大的原因是：

  • 上圖的啟用值統計針對的是一批圖片，不同圖片輸出的啟用值不完全相同，所以圖中是多條曲線而不是一條曲線，曲線中前面一部分資料重合在一起了（紅色虛線），說明不同圖片生成的大部分啟用值其分佈是相似的；但是在曲線的右邊，啟用值比較大時（紅色實現圈起來的部分），曲線不重複了，一個啟用值會對應多個不同的統計量，這時啟用值分佈是比較亂的。
  • 曲線後面啟用值分佈比較亂的部分在整個網路層佔是佔少數的（比如 \(10^-9\), \(10^-7\), \(10^-3\)），因此曲線後面的啟用值分佈部分可以不考慮到對映關係中，只保留啟用值分佈的主方向。

一般認為量化之後的資料分佈與量化前的資料分佈越相似，量化對原始資料資訊的損失也就越小，即量化演演算法精度越高。KL 距離(也叫 KL 散度)一般被用來度量兩個分佈之間的相似性。這裡的資料分佈都是離散形式的，其離散資料的 KL 散度公式如下：

\[D_{KL}(P \| Q) = \sum_i P(i)log_{a} \frac{P(i)}{Q(i)} = \sum_i P(i)[logP(x) - log Q(x)] \]

式中 P 和 Q 分佈表示量化前 FP32 的資料分佈和量化後的 INT8 資料分佈。注意公式要求 P、Q 兩個統計直方圖長度一樣（也就是 bins 的數量一樣）。

TensorRT 使用 KL 散度演演算法進行量化校準的過程：首先在校準集上執行 FP32 推理，然後對於網路每一層執行以下步驟：

  1. 收集啟用輸出的直方圖。
  2. 生成許多具有不同飽和度閾值的量化分佈。
  3. 選擇最小化 KL_divergence(ref_distr, quant_distr) 的閾值 T，並確定 Scale。

以上使用校準集的模型量化過程通常只需幾分鐘時間。

3.5，總結

  • 對稱的，不飽和的線性量化，會導致精度損失較大；
  • 通過最小化 KL 散度來選擇 飽和量化中的 閾值 |T|;

4，量化實戰經驗

參考【商湯泰坦公開課】模型量化了解一下？

1，量化是一種已經獲得了工業界認可和使用的方法，在訓練 (Training) 中使用 FP32 精度，在推理 (Inference) 期間使用 INT8 精度的這套量化體系已經被包括 TensorFlow，TensorRT，PyTorch，MxNet 等眾多深度學習框架和啟用，地平線機器人、海思、安霸等眾多 AI 晶片廠商也在深度學習工具鏈中提供了各自版本的模型量化功能。
2，量化是一個大部分硬體平臺都會支援的，因此比較常用；知識蒸餾有利於獲得小模型，還可以進一步提升量化模型的精度，所以這個技巧也會使用，尤其是在有已經訓好比較強的大模型的基礎上會非常有用。剪枝用的會相對較少，因為可以被網路結構搜尋覆蓋。

參考資料