資料結構高階--AVL(平衡二元樹)(圖解+實現)
AVL樹(平衡二元樹)
概念
二元搜尋樹雖可以縮短查詢的效率,但如果資料有序或接近有序二元搜尋樹將退化為單支樹,查詢元素相當於在順序表中搜尋元素,效率低下。因此為了解決這個問題,兩位俄羅斯的數學家發明了一種方法:當向二元搜尋樹中插入新結點後,如果能保證每個結點的左右子樹高度之差的絕對值不超過1(需要對樹中的結點進行調整),即可降低樹的高度,從而減少平均搜尋長度。
- 它的左右子樹都是AVL樹
- 左右子樹高度之差的絕對值(也叫平衡因子)不超過1
- 我規定:平衡因子(balance factor)= 右子樹高度 - 左子樹高度(後面這樣實現)
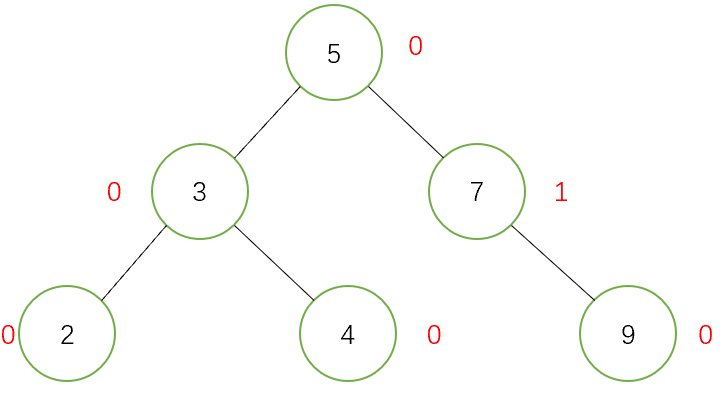
AVL樹節點定義以及框架
template <class K,class V>
struct AVL_Node
{
//三叉鏈
AVL_Node<K, V>* left;
AVL_Node<K, V>* right;
AVL_Node<K, V>* parent;//用來定位父節點
K key;
V value;
int bf;//平衡因子 = 右子樹 - 左子樹
AVL_Node(const K& key, const V& value):left(nullptr),right(nullptr),parent(nullptr), key(key), value(value),bf(0)
{}
};
template <class K, class V>
class AVL_Tree
{
typedef AVL_Node<K,V> Node;
public:
public:
Node* root = nullptr;
};
AVL樹的插入
方法概述
第一步: 我們先按照二元搜尋樹樹插入節點的方式,插入節點(這一步很簡單,上一篇部落格介紹過)
第二步: 更新平衡因子,更新平衡因子的過程是一個難點,下面我給大家分析一下整個過程
平衡因子的調節
實際上,我們應該能夠發現,插入一個節點後,它之後影響它祖先的平衡因子(可能是所有祖先,也可能是一部分祖先),下面就是一個分析過程:
第一步: 判斷父親節點是否存在,不存在直接結束,如果存在,且插入節點是它的左孩子,那麼父親節點的平衡因子就減1,如果是父親的右孩子,父親的平衡因子就加1。然後對父親節點的平衡因子進行檢索。
第二步: 繼續對父親節點的平衡因子進行檢索,平衡因子會有以下三種情況
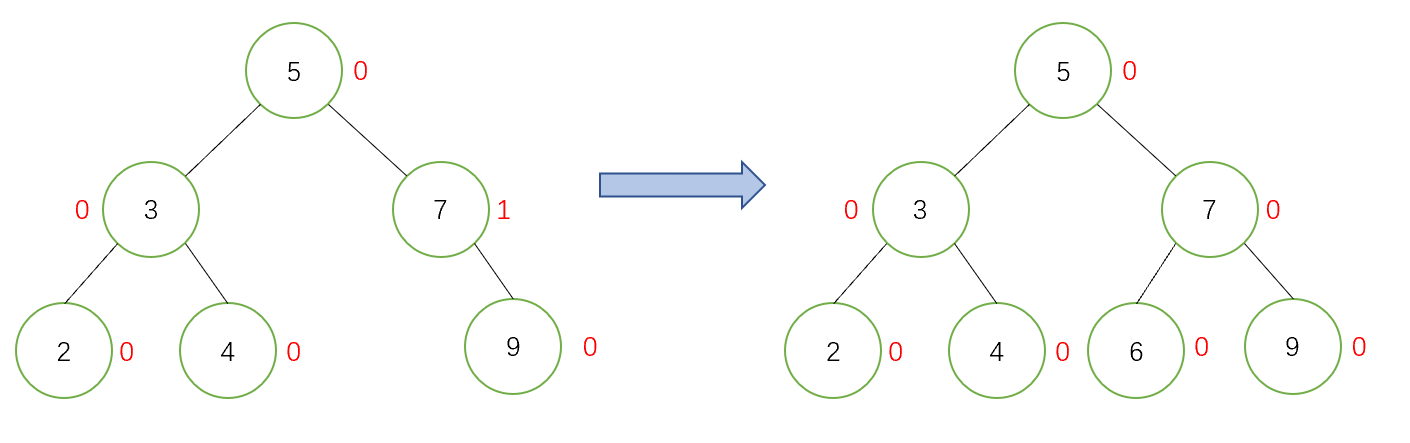
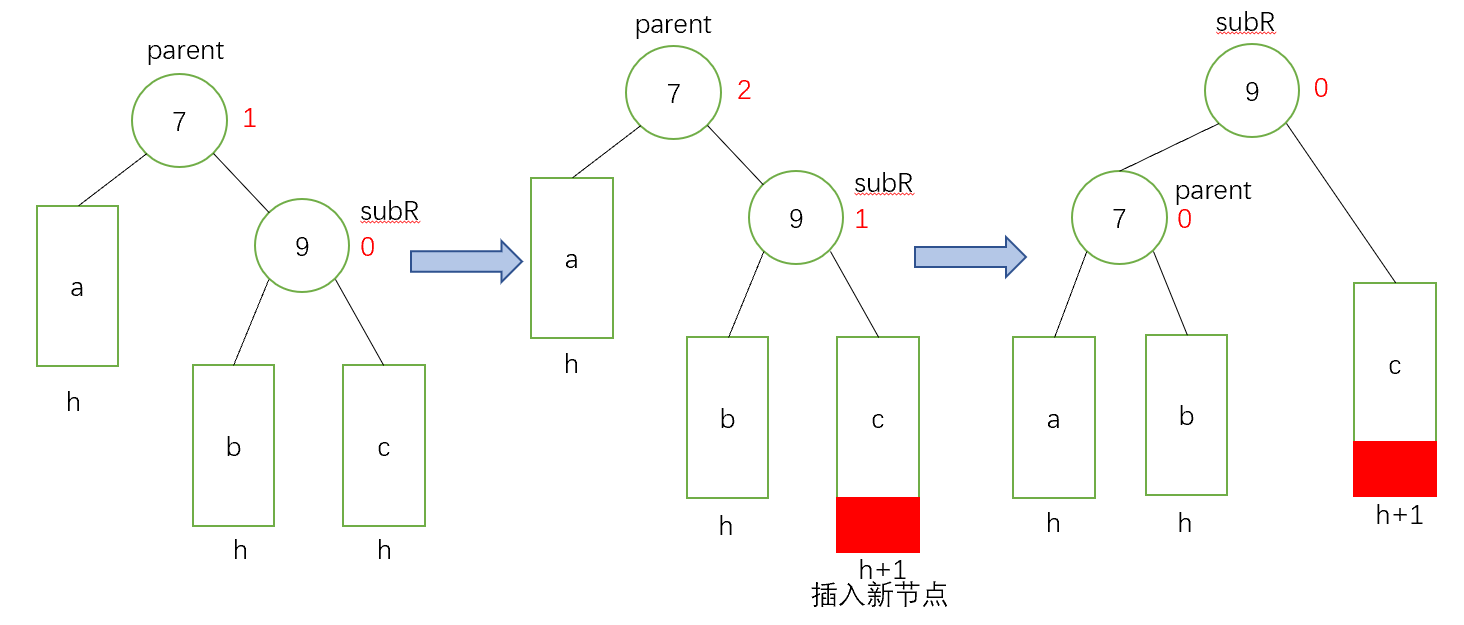
- 第一種情況:此時父親的平衡因子為0,則說明插入前父親的平衡因子為1或-1,缺少左節點或右節點插入後,插入的節點已經補齊了左節點或右節點,整體高度不變,對上層無影響,不需要繼續調節。下面是一個演示圖:
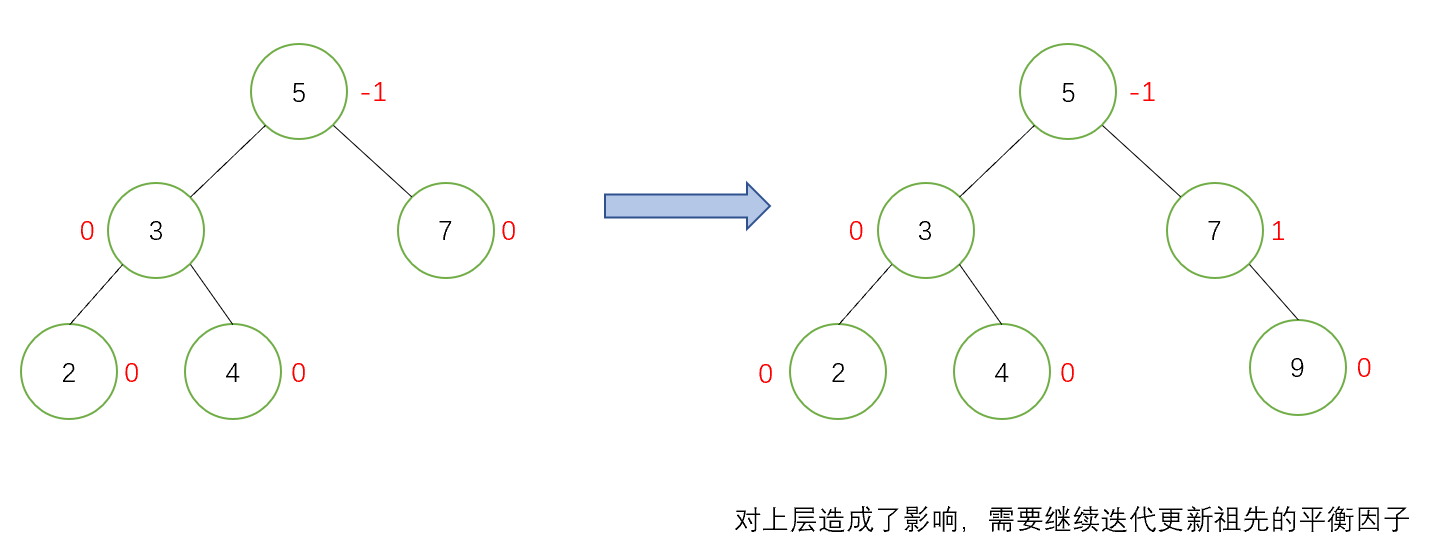
- 第二種情況:此時父親節點的平衡因子為-1或1,則說明插入前父親的平衡因子為0,插入後增加了一個左節點或右節點,整體高度增加1,對上層有影響,繼續迭代更新祖先的平衡因子。下面是一個演示圖:
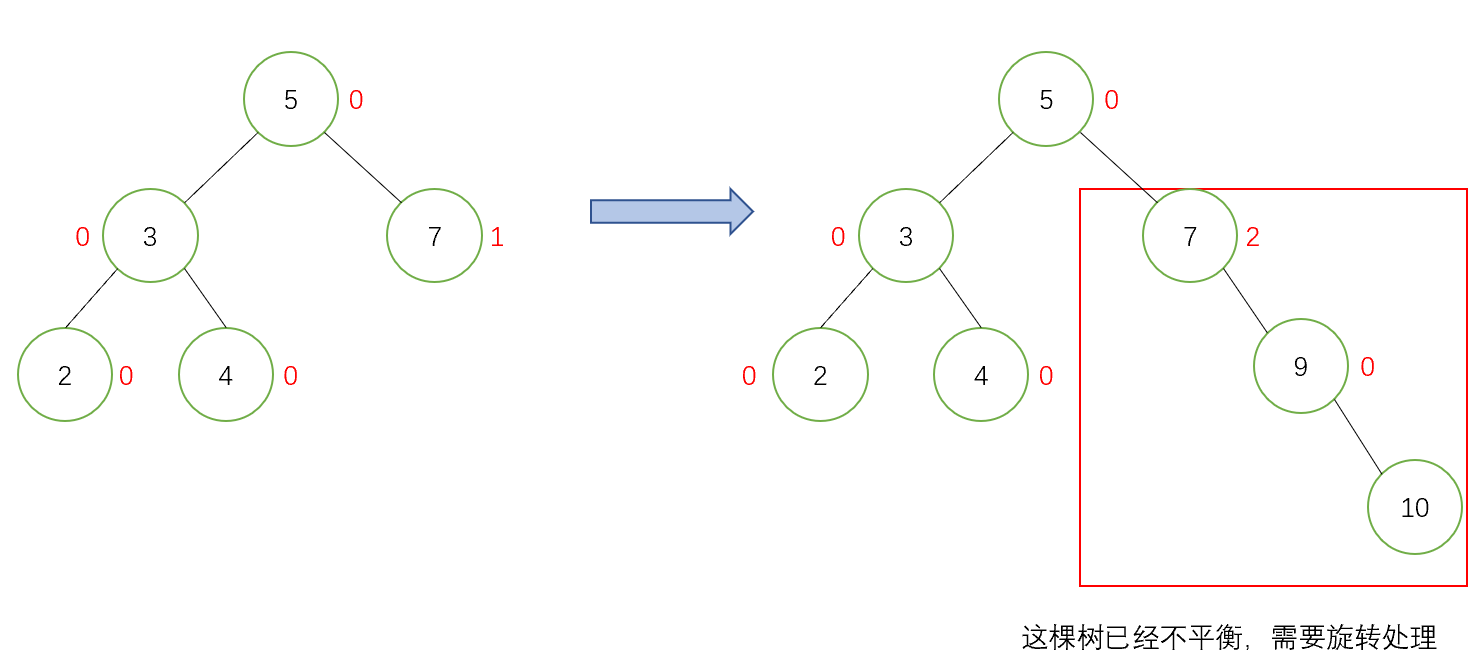
- 第三種情況:此時父親節點的平衡因子為-2或2,則說明插入前父親的平衡因子為-1或1,多了一個左節點或一個右節點,插入後增加了一個左節點或右節點,此時多了兩個左節點和右節點,這棵子樹一邊已經被拉高了,此時這棵子樹不平衡了,需要旋轉處理。下面是一個演示圖:
旋轉處理(出現了不平衡子樹)
一般來說,第一個發生不平衡的節點,我們記作parent,它的孩子分別記作subL(左子樹)和subR(右子樹)
分四種情況討論:
- 左單旋(新插入的節點在右子樹的右側)
具體步驟: 讓subR的左孩子成為parent的右孩子,然後讓parent成為subR的左孩子,最後把兩個節點的平衡因子修改為0。
先畫一個具像圖給大家演示如何進行這個操作(下面是一部分失衡的子樹)
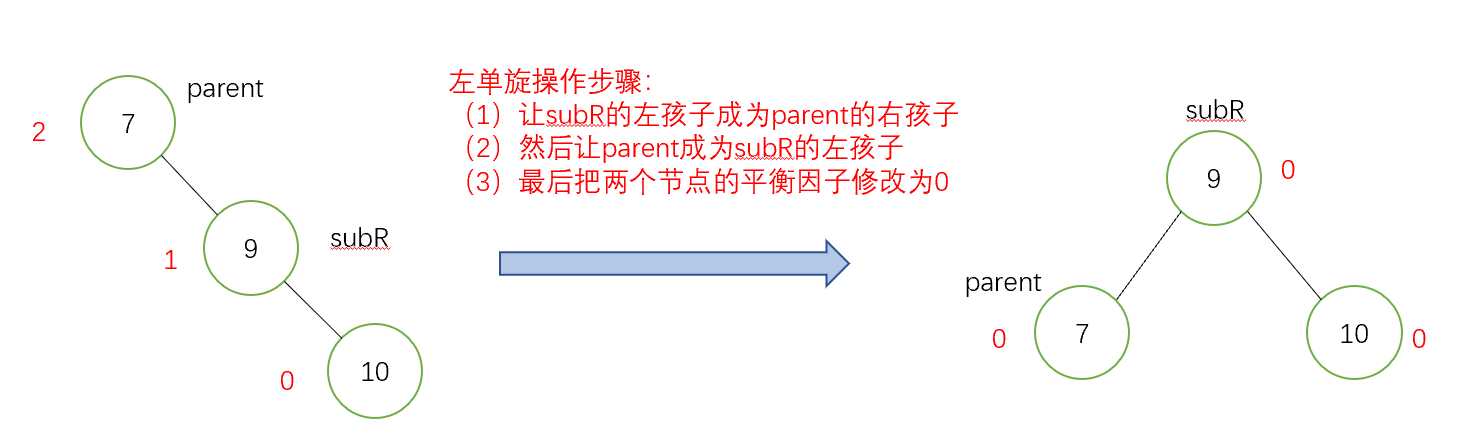
抽象圖:
程式碼實現如下
/*
注意:一般選取第一個不平衡的節點作為parent
*/
//左單旋,新插入的節點在右子樹的右側
/*
步驟:
1.讓subR的左孩子成為parent的右孩子
2.然後讓parent成為subR的左孩子
3.最後把兩個節點的平衡因子修改為0
*/
void RotateL(Node* parent)
{
Node* subR = parent->right;
Node* subRL = subR->left;
//1.先把subR左邊(可能為空也可能不為空)作為parent的右邊
parent->right = subRL;
//2.如果subRL不為空,那麼就讓subRL的父指標指向parent
if (subRL)
{
subRL->parent = parent;
}
//3.先記錄parent的父節點的位置,然後把parent作為subR的左邊
Node* ppNode = parent->parent;
subR->left = parent;
//4.parent的父指標指向subR
parent->parent = subR;
//5.如果ppNode為空-->說明subR現在是根節點,就讓subR的父指標指向nullptr
//如果不是根節點就把subR的父指標指向parent的父節點,parent的父節點(左或右)指向subR
if (ppNode == nullptr)
{
//更新根節點
root = subR;
subR->parent = nullptr;
}
else
{
//判斷parent是ppNode的左還是右
if (ppNode->left == parent)
{
ppNode->left = subR;
}
else
{
ppNode->right = subR;
}
subR->parent = ppNode;
}
//6.把parent和subR的平衡因子更新為0
subR->bf = parent->bf = 0;
}
- 右單旋(新節點插入到左子樹的左側)
具體步驟: 讓subL的右孩子成為parent的左孩子,然後讓parent成為subL的右孩子,最後把兩個節點的平衡因子修改為0
先畫一個具像圖給大家演示如何進行這個操作(下面是一部分失衡的子樹):

抽象圖:
程式碼實現如下:
//右單旋,新插入的節點在左子樹的左側
/*
步驟:
1.讓subL的右孩子成為parent的左孩子
2.然後讓parent成為subL的右孩子
3.最後把兩個節點的平衡因子修改為0
*/
void RotateR(Node* parent)
{
Node* subL = parent->left;
Node* subLR = subL->right;
//1.先把subL的右邊(可能為空也可能不為空)作為parent的左邊
parent->left = subLR;
//2.如果subLR不為空,就把subLR的父指標指向parent
if (subLR)
{
subLR->parent = parent;
}
//3.記錄parent的父節點的位置,然後把parent作為subL的右邊
Node* ppNode = parent->parent;
subL->right = parent;
//4.parent的父親指標指向subL
parent->parent = subL;
//5.如果ppNode為空-->說明subL現在是根節點,就讓subL的父節點指向nullptr
//不是根節點就把subL的父節點指向parent的父節點,parent的父節點(左或右)指向subL
if (ppNode == nullptr)
{
//更新根節點
root = subL;
subL->parent = nullptr;
}
else
{
//判斷parent是ppNode的左還是右
if (ppNode->left == parent)
{
ppNode->left = subL;
}
else
{
ppNode->right = subL;
}
subL->parent = ppNode;
}
//6.把parent和subL的平衡因子更新為0
subL->bf = parent->bf = 0;
}
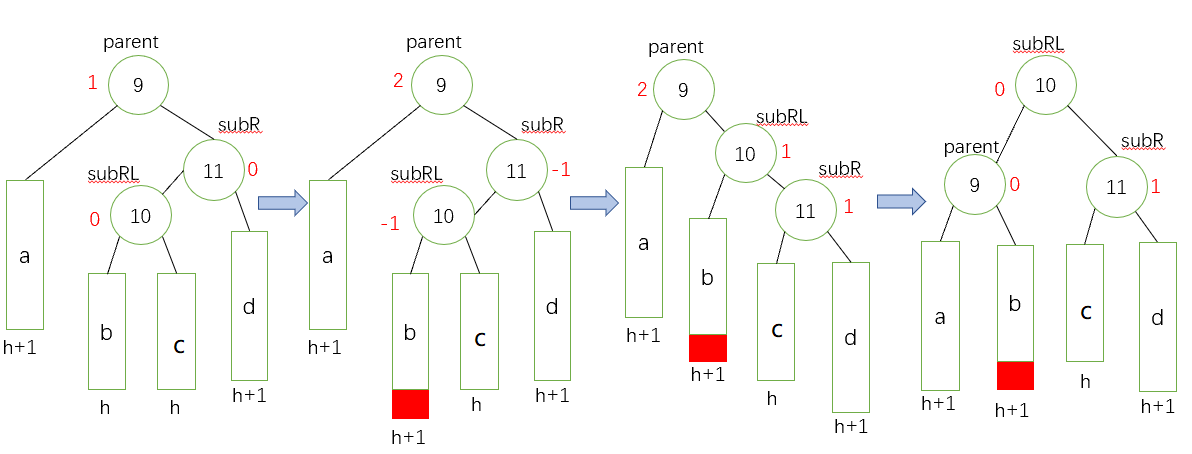
- 右左雙旋(新節點插入在較高右子樹左側,這裡和第一種情況的區別就是前者是直線,後者是折線)
具體步驟 先對subR進行一個右單旋,然後對parent進行左單旋,修改平衡因子,有三種改法。三個節點從左至右的三個節點依次是:parent、subRL和subR。
如果subRL的平衡因子為0,就將它們依次改為0,0, 0;
如果subRL的平衡因子為1,就將它們依次改為-1,0, 0;
如果subRL的平衡因子為-1,就將它們依次改為0,0, 1。
先畫一個具像圖給大家演示如何進行這個操作(下面是一部分失衡的子樹)
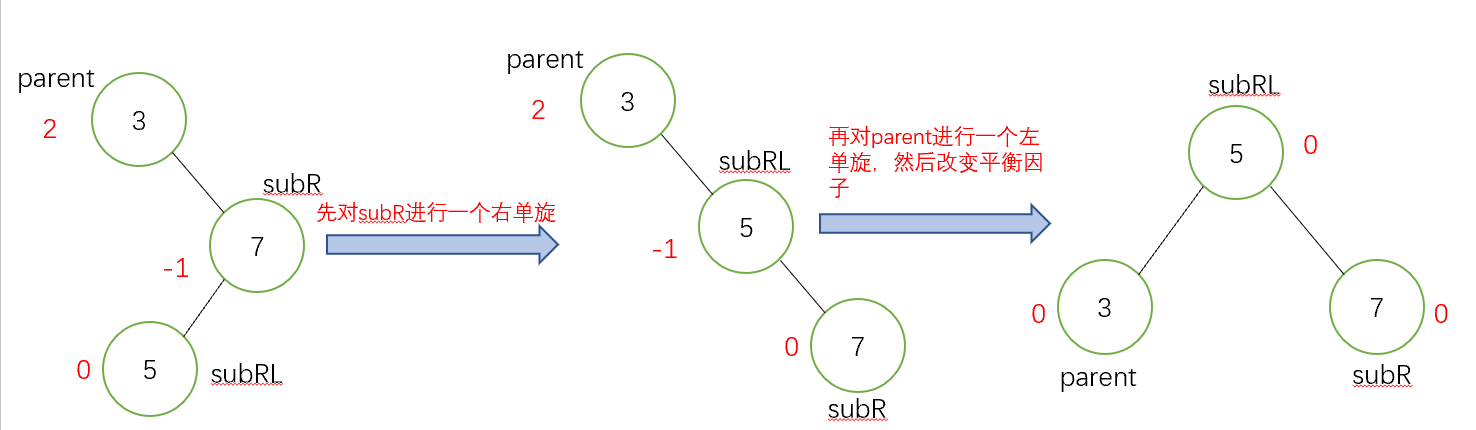
抽象圖(兩種情況):
subRL的bf為1
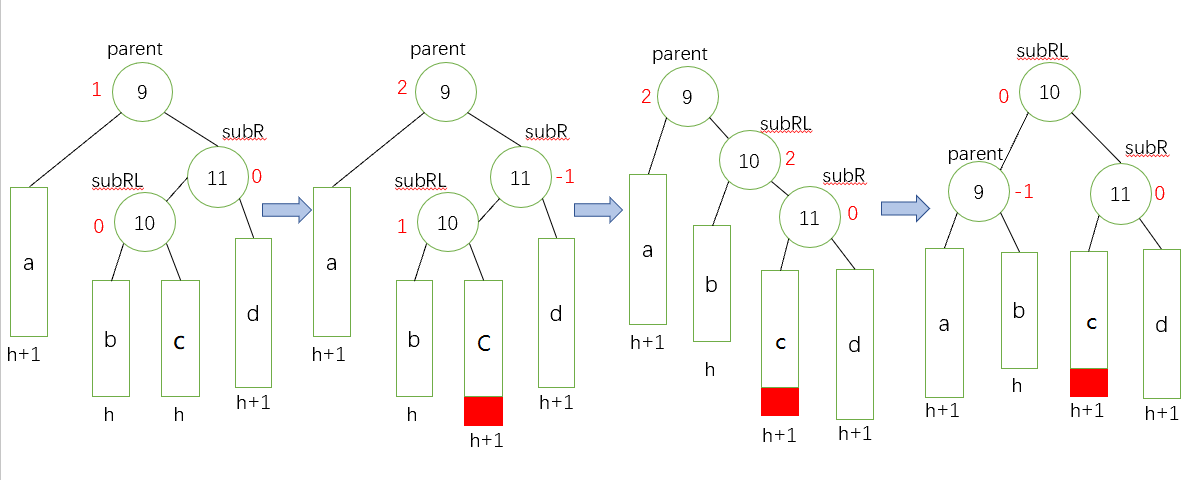
subRL的bf為-1
 **程式碼實現如下:**
**程式碼實現如下:**
//右左雙旋,新插入的節點在右子樹的左側
/*
步驟:
1.先對subR進行一個右單旋
2在對parent進行一個左單旋然後修改平衡因子
*/
void RotateRL(Node* parent)
{
Node* subR = parent->right;
Node* subRL = subR->left;
int bf = subRL->bf;//保留subRL的平衡因子的值,方便直到新插入的節點是在subRL左子樹還是右子樹
//旋轉 先對subR進行右旋轉,再對parent進行左旋轉
RotateR(subR);
RotateL(parent);
// 從左到右 parent subRL subR
if (bf == -1)// subRL的左子樹 bf: 0 0 1
{
parent->bf = 0;
subRL->bf = 0;
subR->bf = 1;
}
else if (bf == 1)// subRL的右子樹 bf: -1 0 0
{
parent->bf = -1;
subRL->bf = 0;
subR->bf = 0;
}
else if (bf == 0)
{
parent->bf = 0;
subRL->bf = 0;
subR->bf = 0;
}
}
- 左右雙旋(新節點插入在較高右子樹左側,這裡和第一種情況的區別就是前者是直線,後者是折線)
具體步驟先對subL進行一個左單旋,然後對parent進行右單旋,修改平衡因子,有三種改法。三個節點從左至右的三個節點一次是:subL、subLR和parent。(和上面的類似,這樣有助於我們記住平衡因子的調整,同時我們也可以畫簡圖理解記憶)
如果subLR的平衡因子為0,就將它們依次改為0,0, 0;
如果subLR的平衡因子為1,就將它們依次改為-1,0, 0;
如果subLR的平衡因子為-1,就將它們依次改為0,0, 1。
先畫一個具像圖給大家演示如何進行這個操作(下面是一部分失衡的子樹)
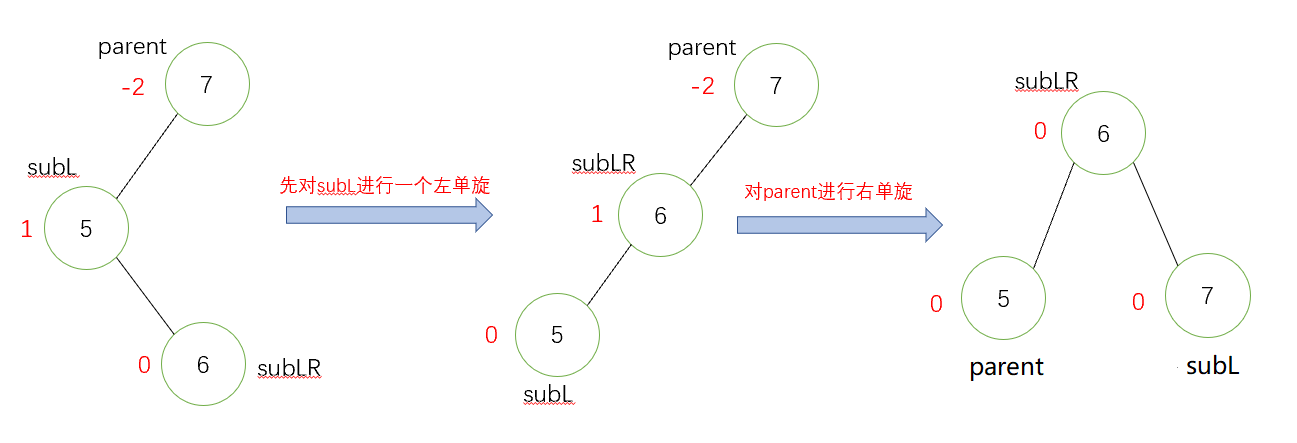
抽象圖(兩種情況):
subLR的bf為-1
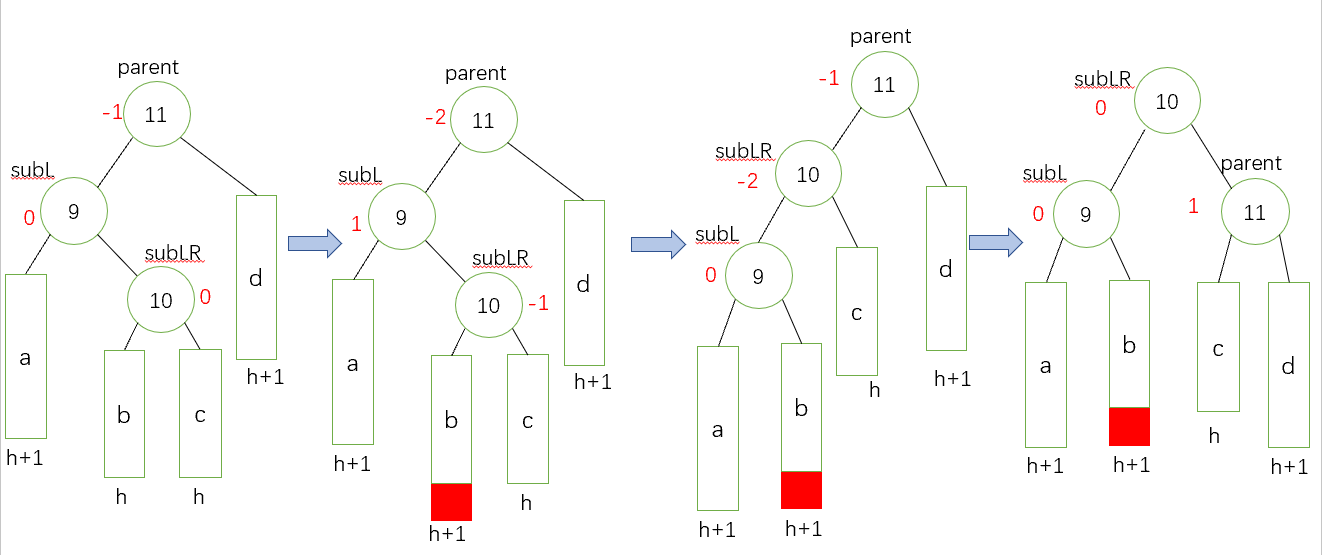
subLR的bf為1
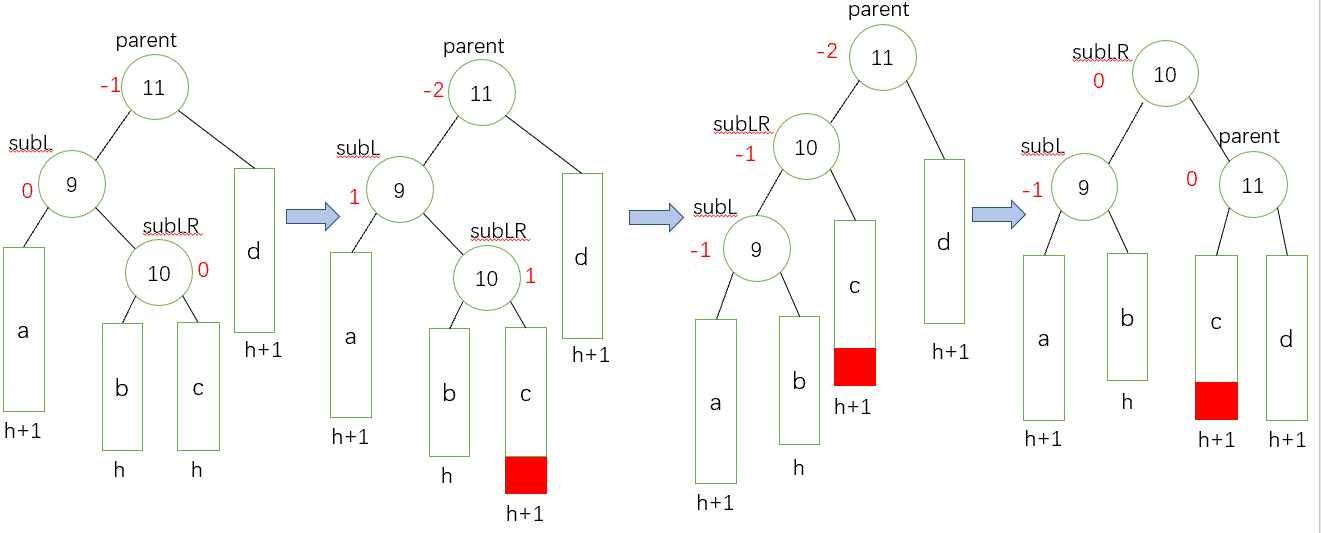
程式碼實現如下:
//左右雙旋,新插入的節點在左子樹的右側
/*
步驟:
1.先對subR進行一個左單旋
2.在對parent進行一個右單旋然後修改平衡因子
*/
void RotateLR(Node* parent)
{
Node* subL = parent->left;
Node* subLR = subL->right;
int bf = subLR->bf;//保留subLR的平衡因子的值,方便直到新插入的節點是在subLR左子樹還是右子樹
//旋轉先對subL進行左旋轉,再對parent進行右旋轉
RotateL(subL);
RotateR(parent);
//從左到右 subL subLR parent
if (bf == -1)// subLR的左子樹 bf: 0 0 1
{
subL->bf = 0;
subLR->bf = 0;
parent->bf = 1;
}
else if (bf == 1)// subLR的右子樹 bf: -1 0 0
{
subL->bf = -1;
subLR->bf = 0;
parent->bf = 0;
}
else if (bf == 0)
{
subL->bf = 0;
subLR->bf = 0;
parent->bf = 0;
}
}
插入程式碼的實現
//二元樹的插入
bool Insert(const K& key, const V& value)
{
//先按照二元搜尋樹一樣插入元素
//無節點插入
if (root == nullptr)
{
root = new Node(key,value);
return true;
}
//有節點時插入
Node* parent = nullptr;
Node* cur = root;
while (cur)
{
parent = cur;
//小於往左走
if (key < cur->key)
{
cur = cur->left;
}
//大於往右走
else if (key > cur->key)
{
cur = cur->right;
}
else
{
//找到了,就返回false
return false;
}
}
cur = new Node(key,value);
// 判斷cur應該插在parent的左還是右
// 小於在左,大於在右
if (cur->key < parent->key)
{
parent->left = cur;
cur->parent = parent;
}
else
{
parent->right = cur;
cur->parent = parent;
}
// 更新parent的平衡因子
// 節點的插入只會影響cur的祖先的平衡因子(不是所有的,是一部分,分情況)
while (parent)
{
// 更新parent的平衡因子
// cur在parent的左,parent->bf--
// cur在parent的右,parent->bf++
if (cur == parent->left)
parent->bf--;
else
parent->bf++;
// bf 可能為 -2、-1、0、1、2
// 如果平衡因子為0,說明更新之前,parent的bf為-1或1,現在補齊了左節點或右節點,bf==0,對上層無影響
// 如果平衡因子為-1或1,說明更新之前,parent的bf為0,現在增加了一個左節點或有節點,bf==-1 || bf==1,對上層有影響
// 如果平衡因子為-2或2,說明更新之前,parent的bf為-1或1,現在往左(右)節點補了左(右)節點,也就是一邊
// 拉高了,樹不平衡了,需要用左旋轉或右旋轉來進行調整
if (parent->bf == 0)
{
//對上層沒有影響,退出
break;
}
else if(parent->bf == -1 || parent->bf == 1)
{
// 對上層有影響,迭代更新
cur = parent;
parent = parent->parent;
}
else
{
// 平衡樹出現了問題,需要調整
// 1.右邊高,左旋轉調整
if (parent->bf == 2)
{
// 如果是一條直線==>左旋轉即可
// 如果是一條折線==>右左旋轉
if (cur->bf == 1)
RotateL(parent);
else if (cur->bf == -1)
RotateRL(parent);
}
// 2.左邊高,右旋轉調整
else if (parent->bf == -2)
{
// 如果是一條直線==>右旋轉即可
// 如果是一條折線==>左右旋轉
if (cur->bf == -1)
RotateR(parent);
else if (cur->bf == 1)
RotateLR(parent);
}
// 調整後是平衡樹,bf為0,不需要調整了
break;
}
}
return true;
}
AVL樹的刪除
方法概述
第一步: 我們先按照二元搜尋樹樹刪除節點的方式,刪除節點(這一步很簡單,上一篇部落格介紹過)
第二步: 然後根據對應刪除情況更新平衡因子,這裡更新平衡因子的方法與插入的更新方法是相反的,下面我給大家分析一下整個過程
平衡因子調節
原則:旋轉的方向取決於是結點parent的哪一棵子樹被縮短。且把第一個不平衡的節點設為parent節點。
刪除節點後,如果刪除的節點為根節點,就結束。否則根據刪除節點為父節點的左右調整父節點的平衡因子。如果刪除節點是父節點的左孩子,那麼父親節點的平衡因子加1,否則減1。然後對父親節點進行檢索。
有以下幾種情況:
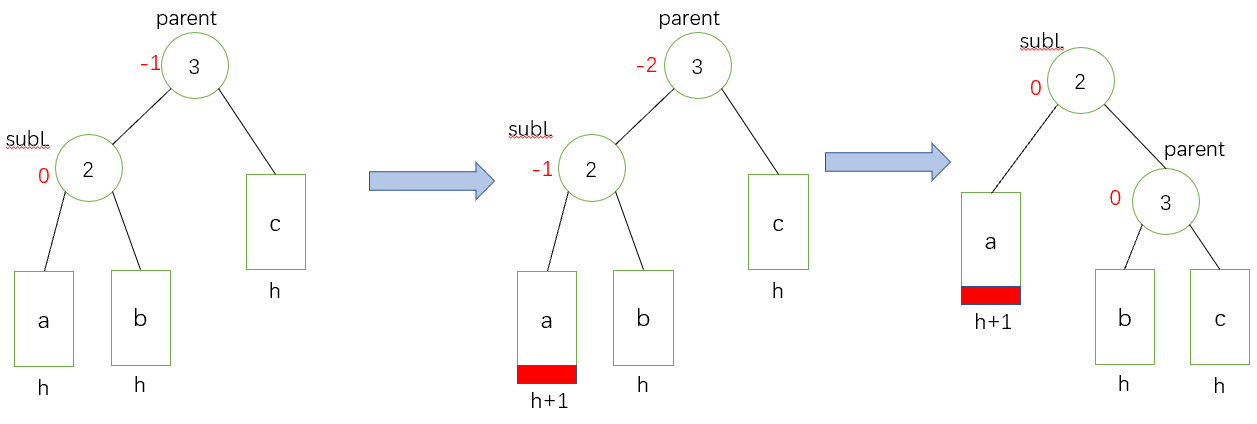
第一種情況:此時父親的平衡因子為0,則說明刪除前父親的平衡因子為1或-1,多出一個左節點或右節點,刪除節點後,左右高度相等,整體高度減1,對上層有影響,需要繼續調節。下面是一個演示圖:(如果此時3為根節點,那麼也可以結束)
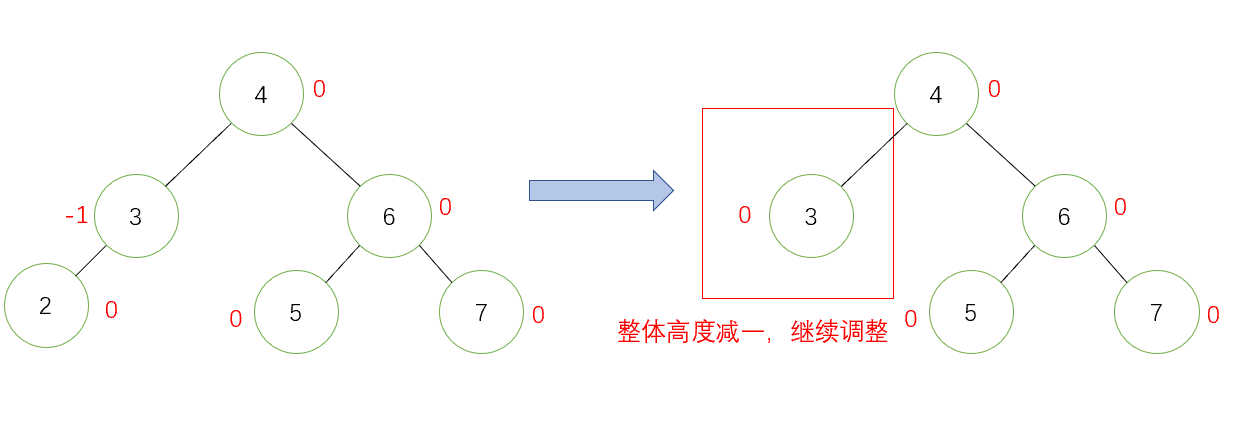
第二種情況:此時父親的平衡因子為-1或1,則說明刪除前父親的平衡因子為0,左右高度相等,刪除節點後,少了一個左節點或右節點,但是整體高度不變,對上層無影響,不需要繼續調節。下面是一個演示圖:
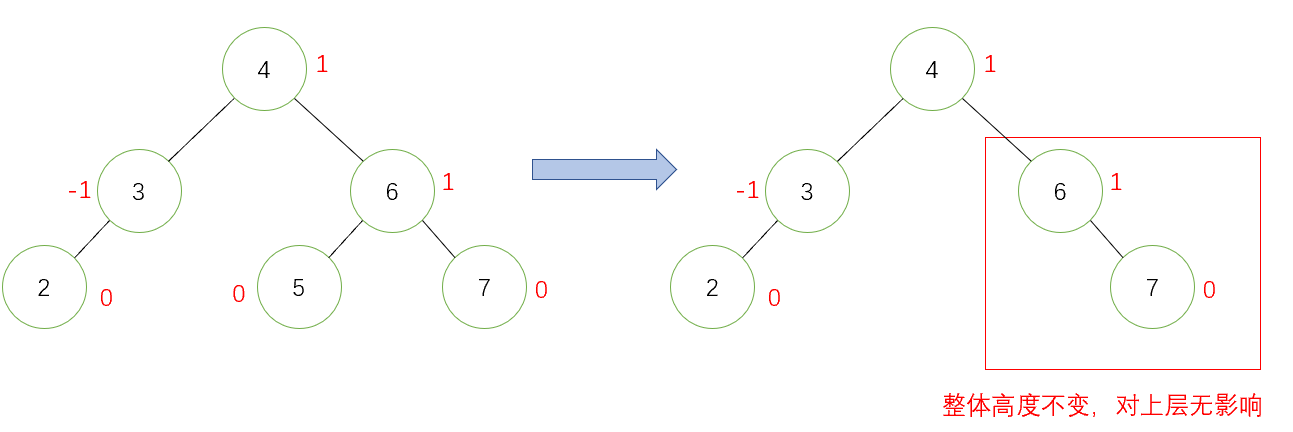
第三種情況: 此時父親節點的平衡因子為-2或2,則說明刪除前父親的平衡因子為-1或1,多了一個左節點或一個右節點,刪除了一個右節點或左節點,此時多了兩個左節點或右節點,這棵子樹一邊已經被拉高了,此時這棵子樹不平衡了,需要旋轉處理。下面是一個演示圖:
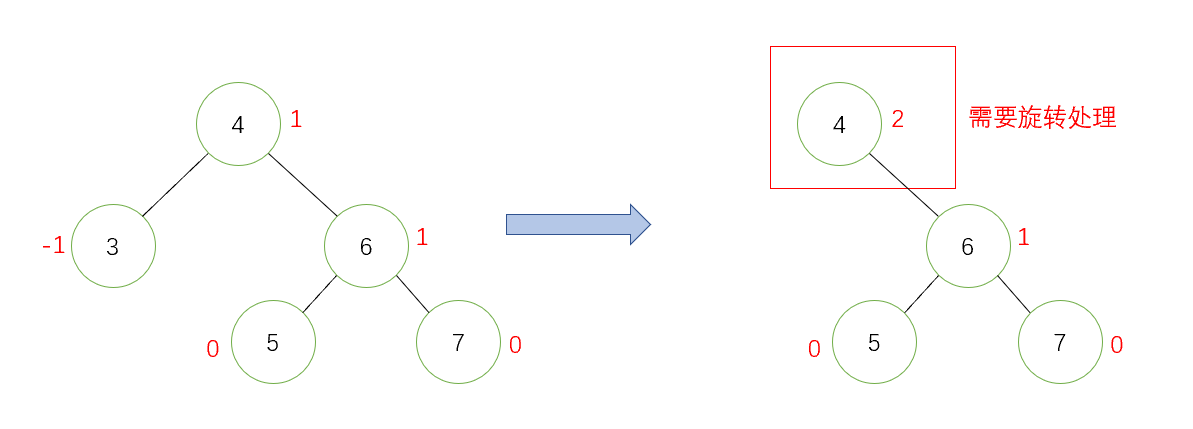
旋轉處理
這裡我只分析右邊高的情況,左邊高和它對稱的,操作是相同的。
情況一:若還未刪除的時候,parent的平衡因子和subR的平衡因子相同,則執行一個單旋轉來恢復平衡
操作方法: 對parent進行左旋轉,因為subR的平衡因子為0,需要繼續檢索,然後繼續迭代,把cur迭代sub的位置,parent到cur的父親的位置
抽象圖:
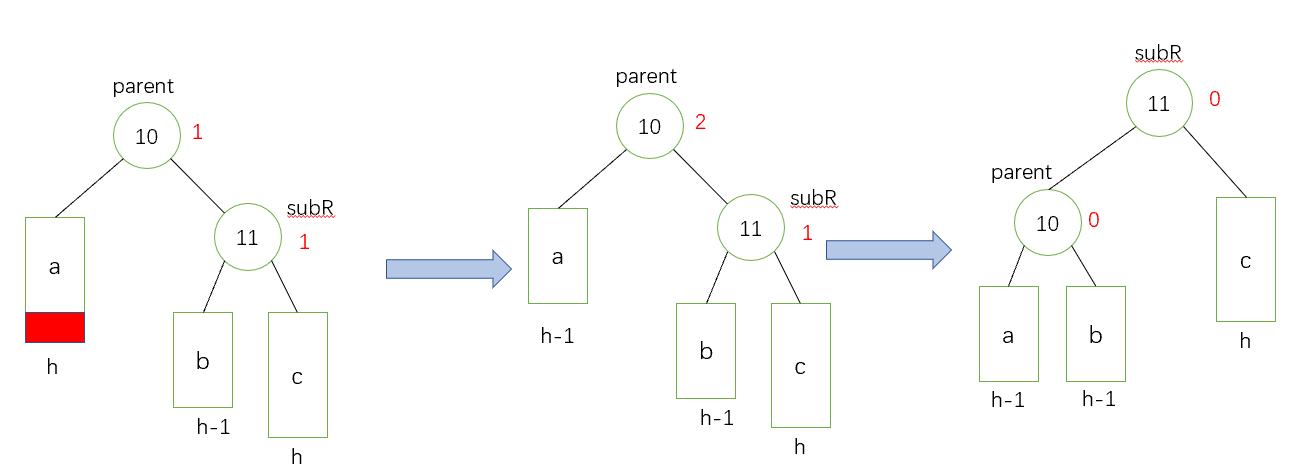
情況二:若還未刪除的時候,subR的平衡因子為0,那麼執行一個單旋轉來恢復parent的平衡
操作方法: 對parent進行左旋,然後修改平衡因子,把subR的平衡因子改為-1,parent的平衡因子改為1,因為subR的平衡因子為-1,所以無需迭代,直接結束
抽象圖:
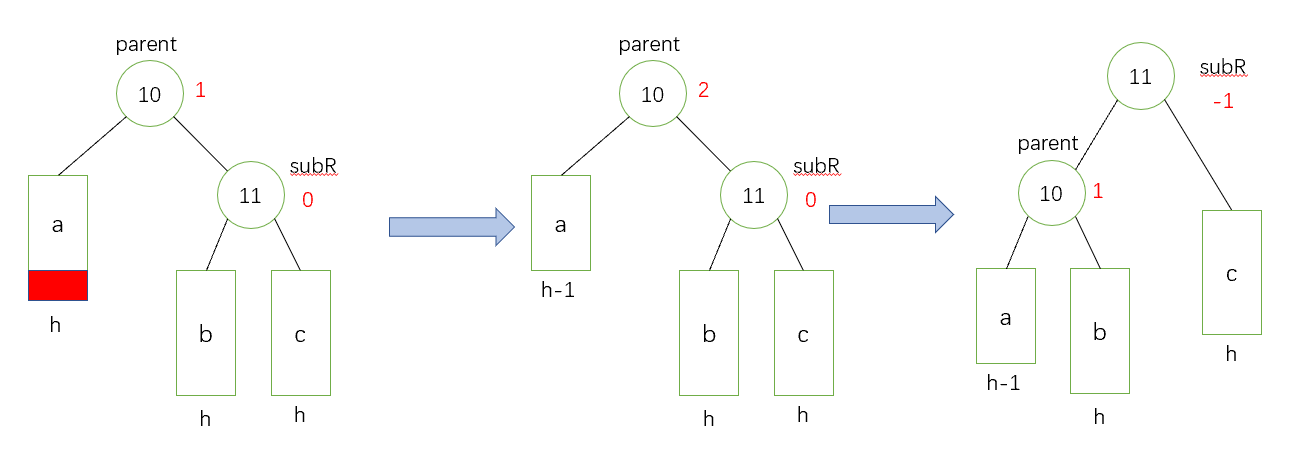
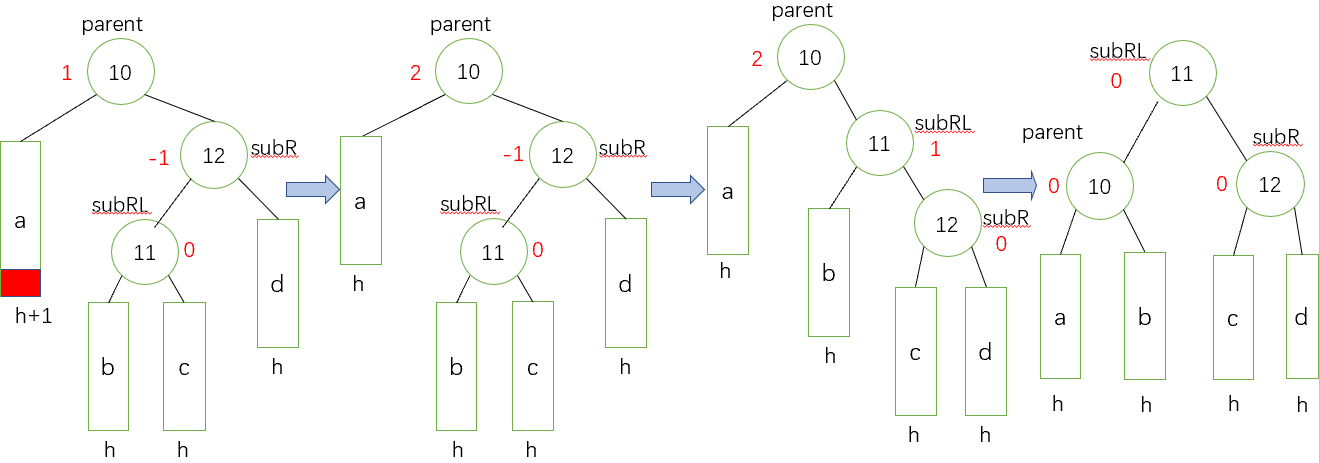
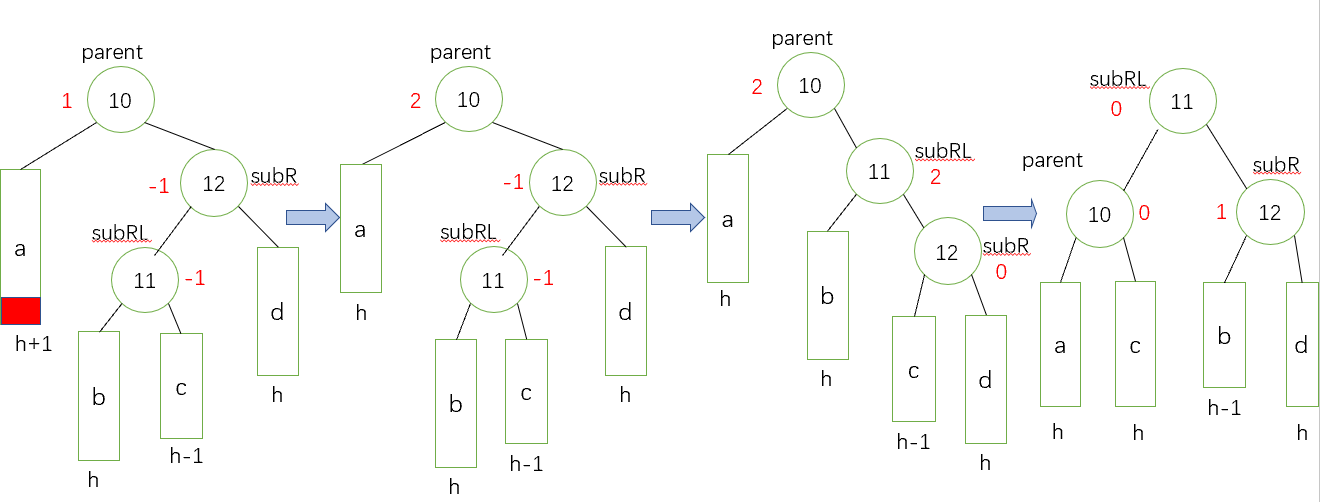
情況三:若還未刪除的時候,parent和subR的平衡因子相反,那麼就執行一個雙旋轉來恢復平衡,先圍繞subR旋轉,再圍繞parent旋轉
操作方法: 對subR進行右旋,然後對parent進行左旋,此時subR的平衡因子為0,需迭代
抽象圖:(三種情況)對應上面的右左雙旋
如果subRL的平衡因子為0,就將它們依次改為0,0, 0;
如果subRL的平衡因子為1,就將它們依次改為-1,0, 0;
如果subRL的平衡因子為-1,就將它們依次改為0,0, 1。
值得注意的是,這三種情況最後的平衡樹subRL均為0,對應這我們講的第一種情況,subRL為0,說明它只有一個左子樹或只有一個右子樹,被刪除了,那麼高度必然發生變化,一旦高度發生變化,就必須向上迭代調整上面的節點的平衡因子,將其調整成-1或者1的時候,徹底平衡,不需要再繼續調整,因為父親節點是-1或者1,說明刪除前它的左右子樹均存在,那麼刪除其中一棵樹不會影響樹的高度,所以依舊不會對上面的節點的平衡因子產生影響,所以只有當調整後subRL的節點是-1和1的時候,才是真正平衡的時候
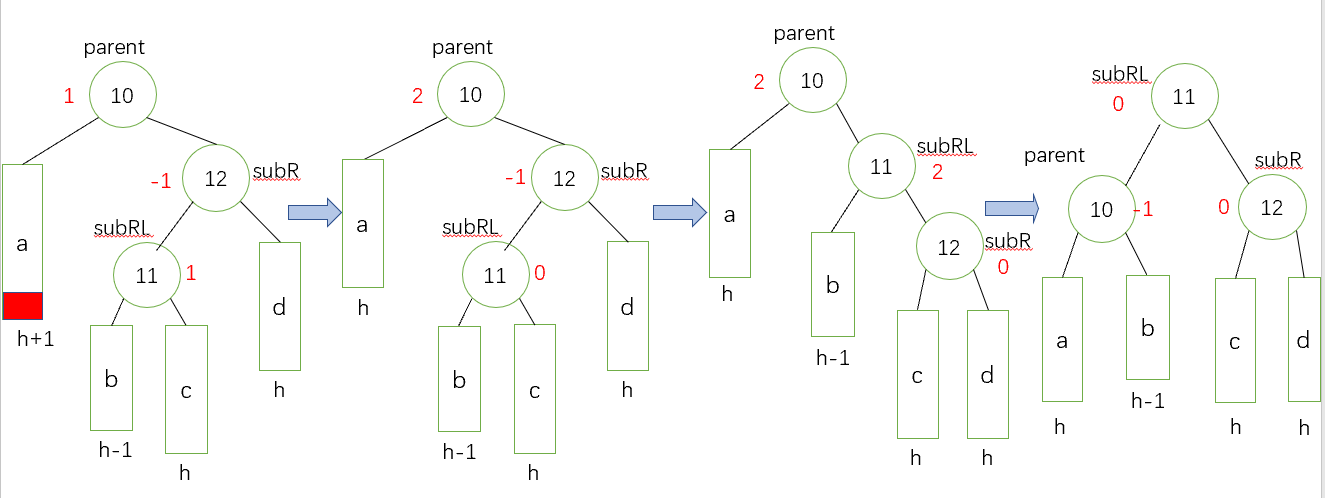
刪除程式碼的實現
//二元搜尋樹的刪除
bool Erase(const K& key)
{
//樹為空,刪除失敗
if (root == nullptr)
{
return false;
}
//parent始終是cur的父親節點
//cur就是要找的刪除的當前節點
Node* parent = nullptr;
Node* cur = root;
while (cur)
{
//小於往左邊走
if (key < cur->key)
{
parent = cur;
cur = cur->left;
}
//大於往右走
else if (key > cur->key)
{
parent = cur;
cur = cur->right;
}
else
{
// 找到了,開始刪除
// 1.左右子樹都為空,直接刪除,可以歸類為左為空
// 2.左右子樹只有一邊為空,左為空,父親指向我的右,右為空,父親指向我的左
// 3.左右子樹都不為空,取左子樹最大的節點或右子樹最小的節點和要刪除的節點交換,然後再刪除
//當前情況是情景三,刪除的節點它的左為空,右未知
if (cur->left == nullptr)
{
// 要刪除節點為根節點時,直接把右子樹的根節點賦值給——root
// 根節點的話會導致parent為nullptr
if (root == cur)
{
root = root->right;
delete cur;
break;
}
else
{
//左為空,父親指向我的右
//判斷cur在父親的左還是右
if (parent->left == cur)
{
parent->left = cur->right;
//左子樹少了一個節點 ++
parent->bf++;
}
else
{
parent->right = cur->right;
//右子樹少了一個節點 --
parent->bf--;
}
}
if (parent->bf != -1 && parent->bf != 1)
{
AfterEraseUpdateBf(parent);
}
delete cur;
}
//當前情況是情景二,刪除節點它的右為空,左未知
else if (cur->right == nullptr)
{
if (root == cur)
{
root = root->left;
delete cur;
break;
}
else
{
//右為空,父親指向我的左
//判斷cur在父親的左還是右
if (parent->left == cur)
{
parent->left = cur->left;
parent->bf++;
}
else
{
parent->right = cur->left;
parent->bf--;
}
}
if (parent->bf != -1 && parent->bf != 1)
{
AfterEraseUpdateBf(parent);
}
delete cur;
}
//只剩下情景四
else
{
//找右子樹中最小的節點,當前cur就是要刪除的節點
Node* rightMinParent = cur;
Node* rightMin = cur->right;//去右子樹找最小的節點
while (rightMin->left)
{
rightMinParent = rightMin;
rightMin = rightMin->left;//一直往左走,找右子樹最小的節點
}
//替代刪除
cur->key = rightMin->key;
//轉化成了情景三,左孩子為空
if (rightMinParent->left == rightMin)
{
rightMinParent->left = rightMin->right;
rightMinParent->bf++;
}
else
{
rightMinParent->right = rightMin->right;
rightMinParent->bf--;
}
if (rightMinParent->bf != -1 && rightMinParent->bf != 1)
{
AfterEraseUpdateBf(rightMinParent);
}
delete rightMin;
}
return true;
}
}
return false;
}
void AfterEraseUpdateBf(Node* parent)
{
if (parent == nullptr)
{
return;
}
Node* cur = parent;
goto first;
while (parent)
{
// 更新parent的平衡因子
// cur在parent的左,parent->_bf++
// cur在parent的右,parent->_bf--
if (cur == parent->left)
parent->bf++;
else
parent->bf--;
// bf 可能為 -2、-1、0、1、2
// 如果平衡因子為0,說明更新之前,parent的bf為-1或1,現在刪掉了左節點或右節點,整體高度變了,對上層有影響
// 如果平衡因子為-1或1,說明更新之前,parent的bf為0,現在刪掉了一個左節點或有節點,整體高度不變,對上層無影響
// 如果平衡因子為-2或2,說明更新之前,parent的bf為-1或1,現在往左(右)節點補了左(右)節點,也就另一邊
// 拉高了,樹不平衡了,需要用左旋轉或右旋轉來進行調整
first:
//此時是部落格中介紹的第一種情況
if (parent->bf == 0)
{
//對上層有影響,迭代更新
//如果parent是根節點就結束
if (parent->parent == nullptr)
{
break;
}
cur = parent;
parent = parent->parent;
}
//此時是部落格中介紹的第二種情況
else if (parent->bf == -1 || parent->bf == 1)
{
//對上層無影響,退出
break;
}
//只剩下第三種情況
else
{
//平衡樹出現了問題,需要調整
//1.右邊高,左旋轉調整
if (parent->bf == 2)
{
//此時是第三種情況的情景1
/*
對parent進行左旋轉,迭代
*/
if (parent->right->bf == 1)
{
RotateL(parent);
cur = parent->parent;
parent = cur->parent;
}
//此時是第三種情況的情景3
/*
對subR進行右旋轉,然後對parent進行左旋,迭代
*/
else if (parent->right->bf == -1)
{
Node* subR = parent->right;
Node* subRL = subR->left;
RotateRL(parent);
// 不平衡向上調整 注意:bug1(以為調整完就是1或-1了,其實三種情況調整完均為0,需要繼續向上迭代
if (subRL->bf != 1 && subRL->bf != -1)
{
cur = subRL;
parent = cur->parent;
continue;
}
}
//此時是第三種情況的情景2
/*
對parent進行左旋,然後修改平衡因子,把subR的平衡因子改為-1,
parent的平衡因子改為1,因為subR的平衡因子為-1,所以無需迭代
*/
else if (parent->right->bf == 0)
{
RotateL(parent);
parent->bf = 1;
parent->parent->bf = -1;
}
}
// 2.左邊高,右旋轉調整
else if (parent->bf == -2)
{
// 如果是一條直線==>右旋轉即可
// 如果是一條折線==>左右旋轉
if (parent->left->bf == -1)
{
RotateR(parent);
cur = parent->parent;// bug2 cur要變成這個位置是因為選擇後父親的位置變了,畫圖
parent = cur->parent;
continue;//parent不是-1或1就繼續
}
else if (parent->left->bf == 1)// 調整後 s sR p 如果sR是1或-1可以退出
{
Node* s = parent->left;
Node* sR = s->right;
RotateLR(parent);
// 不平衡向上調整 為0時如果parent為根
if (sR->bf != 1 && sR->bf != -1)
{
cur = sR;
parent = cur->parent;
continue;
}
}
else if (parent->left->bf == 0)// 平衡因子要修改,畫圖感受 parent->_parent: 1 parent: -1
{
RotateR(parent);
parent->parent->bf = 1;
parent->bf = -1;
}
}
// 調整後是平衡樹,bf為1或-1,不需要調整了,因為-1和1才是最後真正平衡的狀態
break;
}
}
}
AVL樹的查詢
查詢的程式碼和二元搜尋樹是一樣的,這裡就不過多介紹。
程式碼實現如下:
//AVL樹的查詢
bool Find(const K& key)
{
if (root == nullptr)
return false;
Node* cur = root;
while (cur)
{
// 小於往左走
if (key < cur->key)
{
cur = cur->left;
}
// 大於往右走
else if (key > cur->key)
{
cur = cur->right;
}
else
{
// 找到了
return true;
}
}
return false;
}
AVL樹完整程式碼以及測試
#define _CRT_SECURE_NO_WARNINGS
#include<iostream> //引入標頭檔案
#include<string>//C++中的字串
#include<vector>
using namespace std; //標準名稱空間
template <class K,class V>
struct AVL_Node
{
//三叉鏈
AVL_Node<K, V>* left;
AVL_Node<K, V>* right;
AVL_Node<K, V>* parent;//用來定位父節點
K key;
V value;
int bf;//平衡因子 = 右子樹 - 左子樹
AVL_Node(const K& key, const V& value):left(nullptr),right(nullptr),parent(nullptr), key(key), value(value),bf(0)
{}
};
template <class K, class V>
class AVL_Tree
{
typedef AVL_Node<K,V> Node;
public:
/*
注意:一般選取第一個不平衡的節點作為parent
*/
//左單旋,新插入的節點在右子樹的右側
/*
步驟:
1.讓subR的左孩子成為parent的右孩子
2.然後讓parent成為subR的左孩子
3.最後把兩個節點的平衡因子修改為0
*/
void RotateL(Node* parent)
{
Node* subR = parent->right;
Node* subRL = subR->left;
//1.先把subR左邊(可能為空也可能不為空)作為parent的右邊
parent->right = subRL;
//2.如果subRL不為空,那麼就讓subRL的父指標指向parent
if (subRL)
{
subRL->parent = parent;
}
//3.先記錄parent的父節點的位置,然後把parent作為subR的左邊
Node* ppNode = parent->parent;
subR->left = parent;
//4.parent的父指標指向subR
parent->parent = subR;
//5.如果ppNode為空-->說明subR現在是根節點,就讓subR的父指標指向nullptr
//如果不是根節點就把subR的父指標指向parent的父節點,parent的父節點(左或右)指向subR
if (ppNode == nullptr)
{
//更新根節點
root = subR;
subR->parent = nullptr;
}
else
{
//判斷parent是ppNode的左還是右
if (ppNode->left == parent)
{
ppNode->left = subR;
}
else
{
ppNode->right = subR;
}
subR->parent = ppNode;
}
//6.把parent和subR的平衡因子更新為0
subR->bf = parent->bf = 0;
}
//右單旋,新插入的節點在左子樹的左側
/*
步驟:
1.讓subL的右孩子成為parent的左孩子
2.然後讓parent成為subL的右孩子
3.最後把兩個節點的平衡因子修改為0
*/
void RotateR(Node* parent)
{
Node* subL = parent->left;
Node* subLR = subL->right;
//1.先把subL的右邊(可能為空也可能不為空)作為parent的左邊
parent->left = subLR;
//2.如果subLR不為空,就把subLR的父指標指向parent
if (subLR)
{
subLR->parent = parent;
}
//3.記錄parent的父節點的位置,然後把parent作為subL的右邊
Node* ppNode = parent->parent;
subL->right = parent;
//4.parent的父親指標指向subL
parent->parent = subL;
//5.如果ppNode為空-->說明subL現在是根節點,就讓subL的父節點指向nullptr
//不是根節點就把subL的父節點指向parent的父節點,parent的父節點(左或右)指向subL
if (ppNode == nullptr)
{
//更新根節點
root = subL;
subL->parent = nullptr;
}
else
{
//判斷parent是ppNode的左還是右
if (ppNode->left == parent)
{
ppNode->left = subL;
}
else
{
ppNode->right = subL;
}
subL->parent = ppNode;
}
//6.把parent和subL的平衡因子更新為0
subL->bf = parent->bf = 0;
}
//二元樹的插入
bool Insert(const K& key, const V& value)
{
//先按照二元搜尋樹一樣插入元素
//無節點插入
if (root == nullptr)
{
root = new Node(key,value);
return true;
}
//有節點時插入
Node* parent = nullptr;
Node* cur = root;
while (cur)
{
parent = cur;
//小於往左走
if (key < cur->key)
{
cur = cur->left;
}
//大於往右走
else if (key > cur->key)
{
cur = cur->right;
}
else
{
//找到了,就返回false
return false;
}
}
cur = new Node(key,value);
// 判斷cur應該插在parent的左還是右
// 小於在左,大於在右
if (cur->key < parent->key)
{
parent->left = cur;
cur->parent = parent;
}
else
{
parent->right = cur;
cur->parent = parent;
}
// 更新parent的平衡因子
// 節點的插入只會影響cur的祖先的平衡因子(不是所有的,是一部分,分情況)
while (parent)
{
// 更新parent的平衡因子
// cur在parent的左,parent->bf--
// cur在parent的右,parent->bf++
if (cur == parent->left)
parent->bf--;
else
parent->bf++;
// bf 可能為 -2、-1、0、1、2
// 如果平衡因子為0,說明更新之前,parent的bf為-1或1,現在補齊了左節點或右節點,bf==0,對上層無影響
// 如果平衡因子為-1或1,說明更新之前,parent的bf為0,現在增加了一個左節點或有節點,bf==-1 || bf==1,對上層有影響
// 如果平衡因子為-2或2,說明更新之前,parent的bf為-1或1,現在往左(右)節點補了左(右)節點,也就是一邊
// 拉高了,樹不平衡了,需要用左旋轉或右旋轉來進行調整
if (parent->bf == 0)
{
//對上層沒有影響,退出
break;
}
else if(parent->bf == -1 || parent->bf == 1)
{
// 對上層有影響,迭代更新
cur = parent;
parent = parent->parent;
}
else
{
// 平衡樹出現了問題,需要調整
// 1.右邊高,左旋轉調整
if (parent->bf == 2)
{
// 如果是一條直線==>左旋轉即可
// 如果是一條折線==>右左旋轉
if (cur->bf == 1)
RotateL(parent);
else if (cur->bf == -1)
RotateRL(parent);
}
// 2.左邊高,右旋轉調整
else if (parent->bf == -2)
{
// 如果是一條直線==>右旋轉即可
// 如果是一條折線==>左右旋轉
if (cur->bf == -1)
RotateR(parent);
else if (cur->bf == 1)
RotateLR(parent);
}
// 調整後是平衡樹,bf為0,不需要調整了
break;
}
}
return true;
}
//右左雙旋,新插入的節點在右子樹的左側
/*
步驟:
1.先對subR進行一個右單旋
2在對parent進行一個左單旋然後修改平衡因子
*/
void RotateRL(Node* parent)
{
Node* subR = parent->right;
Node* subRL = subR->left;
int bf = subRL->bf;//保留subRL的平衡因子的值,方便直到新插入的節點是在subRL左子樹還是右子樹
//旋轉 先對subR進行右旋轉,再對parent進行左旋轉
RotateR(subR);
RotateL(parent);
// 從左到右 parent subRL subR
if (bf == -1)// subRL的左子樹 bf: 0 0 1
{
parent->bf = 0;
subRL->bf = 0;
subR->bf = 1;
}
else if (bf == 1)// subRL的右子樹 bf: -1 0 0
{
parent->bf = -1;
subRL->bf = 0;
subR->bf = 0;
}
else if (bf == 0)
{
parent->bf = 0;
subRL->bf = 0;
subR->bf = 0;
}
}
//左右雙旋,新插入的節點在左子樹的右側
/*
步驟:
1.先對subR進行一個左單旋
2.在對parent進行一個右單旋然後修改平衡因子
*/
void RotateLR(Node* parent)
{
Node* subL = parent->left;
Node* subLR = subL->right;
int bf = subLR->bf;//保留subLR的平衡因子的值,方便直到新插入的節點是在subLR左子樹還是右子樹
//旋轉先對subL進行左旋轉,再對parent進行右旋轉
RotateL(subL);
RotateR(parent);
//從左到右 subL subLR parent
if (bf == -1)// subLR的左子樹 bf: 0 0 1
{
subL->bf = 0;
subLR->bf = 0;
parent->bf = 1;
}
else if (bf == 1)// subLR的右子樹 bf: -1 0 0
{
subL->bf = -1;
subLR->bf = 0;
parent->bf = 0;
}
else if (bf == 0)
{
subL->bf = 0;
subLR->bf = 0;
parent->bf = 0;
}
}
//二元搜尋樹的刪除
bool Erase(const K& key)
{
//樹為空,刪除失敗
if (root == nullptr)
{
return false;
}
//parent始終是cur的父親節點
//cur就是要找的刪除的當前節點
Node* parent = nullptr;
Node* cur = root;
while (cur)
{
//小於往左邊走
if (key < cur->key)
{
parent = cur;
cur = cur->left;
}
//大於往右走
else if (key > cur->key)
{
parent = cur;
cur = cur->right;
}
else
{
// 找到了,開始刪除
// 1.左右子樹都為空,直接刪除,可以歸類為左為空
// 2.左右子樹只有一邊為空,左為空,父親指向我的右,右為空,父親指向我的左
// 3.左右子樹都不為空,取左子樹最大的節點或右子樹最小的節點和要刪除的節點交換,然後再刪除
//當前情況是情景三,刪除的節點它的左為空,右未知
if (cur->left == nullptr)
{
// 要刪除節點為根節點時,直接把右子樹的根節點賦值給——root
// 根節點的話會導致parent為nullptr
if (root == cur)
{
root = root->right;
delete cur;
break;
}
else
{
//左為空,父親指向我的右
//判斷cur在父親的左還是右
if (parent->left == cur)
{
parent->left = cur->right;
//左子樹少了一個節點 ++
parent->bf++;
}
else
{
parent->right = cur->right;
//右子樹少了一個節點 --
parent->bf--;
}
}
if (parent->bf != -1 && parent->bf != 1)
{
AfterEraseUpdateBf(parent);
}
delete cur;
}
//當前情況是情景二,刪除節點它的右為空,左未知
else if (cur->right == nullptr)
{
if (root == cur)
{
root = root->left;
delete cur;
break;
}
else
{
//右為空,父親指向我的左
//判斷cur在父親的左還是右
if (parent->left == cur)
{
parent->left = cur->left;
parent->bf++;
}
else
{
parent->right = cur->left;
parent->bf--;
}
}
if (parent->bf != -1 && parent->bf != 1)
{
AfterEraseUpdateBf(parent);
}
delete cur;
}
//只剩下情景四
else
{
//找右子樹中最小的節點,當前cur就是要刪除的節點
Node* rightMinParent = cur;
Node* rightMin = cur->right;//去右子樹找最小的節點
while (rightMin->left)
{
rightMinParent = rightMin;
rightMin = rightMin->left;//一直往左走,找右子樹最小的節點
}
//替代刪除
cur->key = rightMin->key;
//轉化成了情景三,左孩子為空
if (rightMinParent->left == rightMin)
{
rightMinParent->left = rightMin->right;
rightMinParent->bf++;
}
else
{
rightMinParent->right = rightMin->right;
rightMinParent->bf--;
}
if (rightMinParent->bf != -1 && rightMinParent->bf != 1)
{
AfterEraseUpdateBf(rightMinParent);
}
delete rightMin;
}
return true;
}
}
return false;
}
void AfterEraseUpdateBf(Node* parent)
{
if (parent == nullptr)
{
return;
}
Node* cur = parent;
goto first;
while (parent)
{
// 更新parent的平衡因子
// cur在parent的左,parent->_bf++
// cur在parent的右,parent->_bf--
if (cur == parent->left)
parent->bf++;
else
parent->bf--;
// bf 可能為 -2、-1、0、1、2
// 如果平衡因子為0,說明更新之前,parent的bf為-1或1,現在刪掉了左節點或右節點,整體高度變了,對上層有影響
// 如果平衡因子為-1或1,說明更新之前,parent的bf為0,現在刪掉了一個左節點或有節點,整體高度不變,對上層無影響
// 如果平衡因子為-2或2,說明更新之前,parent的bf為-1或1,現在往左(右)節點補了左(右)節點,也就另一邊
// 拉高了,樹不平衡了,需要用左旋轉或右旋轉來進行調整
first:
//此時是部落格中介紹的第一種情況
if (parent->bf == 0)
{
//對上層有影響,迭代更新
//如果parent是根節點就結束
if (parent->parent == nullptr)
{
break;
}
cur = parent;
parent = parent->parent;
}
//此時是部落格中介紹的第二種情況
else if (parent->bf == -1 || parent->bf == 1)
{
//對上層無影響,退出
break;
}
//只剩下第三種情況
else
{
//平衡樹出現了問題,需要調整
//1.右邊高,左旋轉調整
if (parent->bf == 2)
{
//此時是第三種情況的情景1
/*
對parent進行左旋轉,迭代
*/
if (parent->right->bf == 1)
{
RotateL(parent);
cur = parent->parent;
parent = cur->parent;
}
//此時是第三種情況的情景3
/*
對subR進行右旋轉,然後對parent進行左旋,迭代
*/
else if (parent->right->bf == -1)
{
Node* subR = parent->right;
Node* subRL = subR->left;
RotateRL(parent);
// 不平衡向上調整 注意:bug1(以為調整完就是1或-1了,其實三種情況調整完均為0,需要繼續向上迭代
if (subRL->bf != 1 && subRL->bf != -1)
{
cur = subRL;
parent = cur->parent;
continue;
}
}
//此時是第三種情況的情景2
/*
對parent進行左旋,然後修改平衡因子,把subR的平衡因子改為-1,
parent的平衡因子改為1,因為subR的平衡因子為-1,所以無需迭代
*/
else if (parent->right->bf == 0)
{
RotateL(parent);
parent->bf = 1;
parent->parent->bf = -1;
}
}
// 2.左邊高,右旋轉調整
else if (parent->bf == -2)
{
// 如果是一條直線==>右旋轉即可
// 如果是一條折線==>左右旋轉
if (parent->left->bf == -1)
{
RotateR(parent);
cur = parent->parent;// bug2 cur要變成這個位置是因為選擇後父親的位置變了,畫圖
parent = cur->parent;
continue;//parent不是-1或1就繼續
}
else if (parent->left->bf == 1)// 調整後 s sR p 如果sR是1或-1可以退出
{
Node* s = parent->left;
Node* sR = s->right;
RotateLR(parent);
// 不平衡向上調整 為0時如果parent為根
if (sR->bf != 1 && sR->bf != -1)
{
cur = sR;
parent = cur->parent;
continue;
}
}
else if (parent->left->bf == 0)// 平衡因子要修改,畫圖感受 parent->_parent: 1 parent: -1
{
RotateR(parent);
parent->parent->bf = 1;
parent->bf = -1;
}
}
// 調整後是平衡樹,bf為1或-1,不需要調整了,因為-1和1才是最後真正平衡的狀態
break;
}
}
}
//AVL樹的查詢
bool Find(const K& key)
{
if (root == nullptr)
return false;
Node* cur = root;
while (cur)
{
// 小於往左走
if (key < cur->key)
{
cur = cur->left;
}
// 大於往右走
else if (key > cur->key)
{
cur = cur->right;
}
else
{
// 找到了
return true;
}
}
return false;
}
//中序遍歷(遞迴)
void InOrder()
{
_InOrder(root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == NULL)
{
return;
}
else
{
_InOrder(root->left);
cout << root->key << ":" << root->value<<" ";
_InOrder(root->right);
}
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->left);
int rightHeight = _Height(root->right);
return 1 + max(leftHeight, rightHeight);
}
bool _IsBalanceTree(Node* root)
{
if (root == nullptr)
return true;
int leftHeight = _Height(root->left);
int rightHeight = _Height(root->right);
return rightHeight - leftHeight == root->bf
&& abs(rightHeight - leftHeight) < 2
&& _IsBalanceTree(root->left)
&& _IsBalanceTree(root->right);
}
public:
Node* root = nullptr;
};
void TestAVLTree1()
{
AVL_Tree<int, int> at;
//srand((size_t)time(nullptr));
int b[] = { 4,3,5,3,1,2,7 };//出錯
//int b[] = { 1,2,3,4,5,6,7,8,9 };正確
//int b[] = { 2,4,6,3,5,1,9,10,8,7 };正確
//int b[] = {4,2,3,5};//出錯,插入3出錯
//int b[] = { 16,3,7,11,9,26,18,14,15 };//出錯
//int b[] = { 4,2,6,1,3,5,15,7,16,14 };//出錯
// int* a = new int[10000];
/*int i = 1;
for (auto& e : a)
{
e = i++;
}*/
vector<int> a;
for (size_t i = 0; i < sizeof(b)/sizeof(int); ++i)
{
// a.push_back(rand());
a.push_back(b[i]);
}
for (auto e : a)
{
at.Insert(e,e);
cout << "插入 " << e << " 後變化 --> Height: " << at._Height(at.root) << " 是否為AVLTree:" << at._IsBalanceTree(at.root)<<endl;
cout << "列印二元樹: ";
at.InOrder();
}
cout << "------------------------------------------------------" << endl;
// at.InOrder();
for (auto e : a)
{
at.Erase(e);
cout << "刪除 " << e << " 後變化 --> Height: " << at._Height(at.root) << " 是否為AVLTree:" << at._IsBalanceTree(at.root) << endl;
cout << "列印二元樹: ";
at.InOrder();
}
at.InOrder();
}
int main()
{
TestAVLTree1();
system("pause");
return EXIT_SUCCESS;
}