技術文章 » 為什麼計算機中的負數要用二補數表示？

為什麼計算機中的負數要用二補數表示？

2022-12-02 06:00:59

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

前言

大家好，我是小彭。

在前面的文章裡，我們聊到了計算機的馮·諾依曼架構的 3 個基本原則。其中第 1 個原則是計算機中所有資訊都是採用二進位制格式的編碼。也就是說，在計算機中程式的資料和指令，以及使用者輸入的所有資料，計算機都需要把它們轉換為二進位制的格式，才能進行識別和運算。

然而，我們日常生活接觸到的大部分數位卻是十進位制編碼，例如手機號碼、工牌號、學號。那為什麼計算機要使用二進位制數制？二進位制資料如何進行運算，以及計算機做了哪些優化來如何提高運算的效率？今天我們就圍繞這些問題展開。

小彭的 Android 交流群 02 群已經建立啦，掃描文末二維條碼進入~

思維導圖：

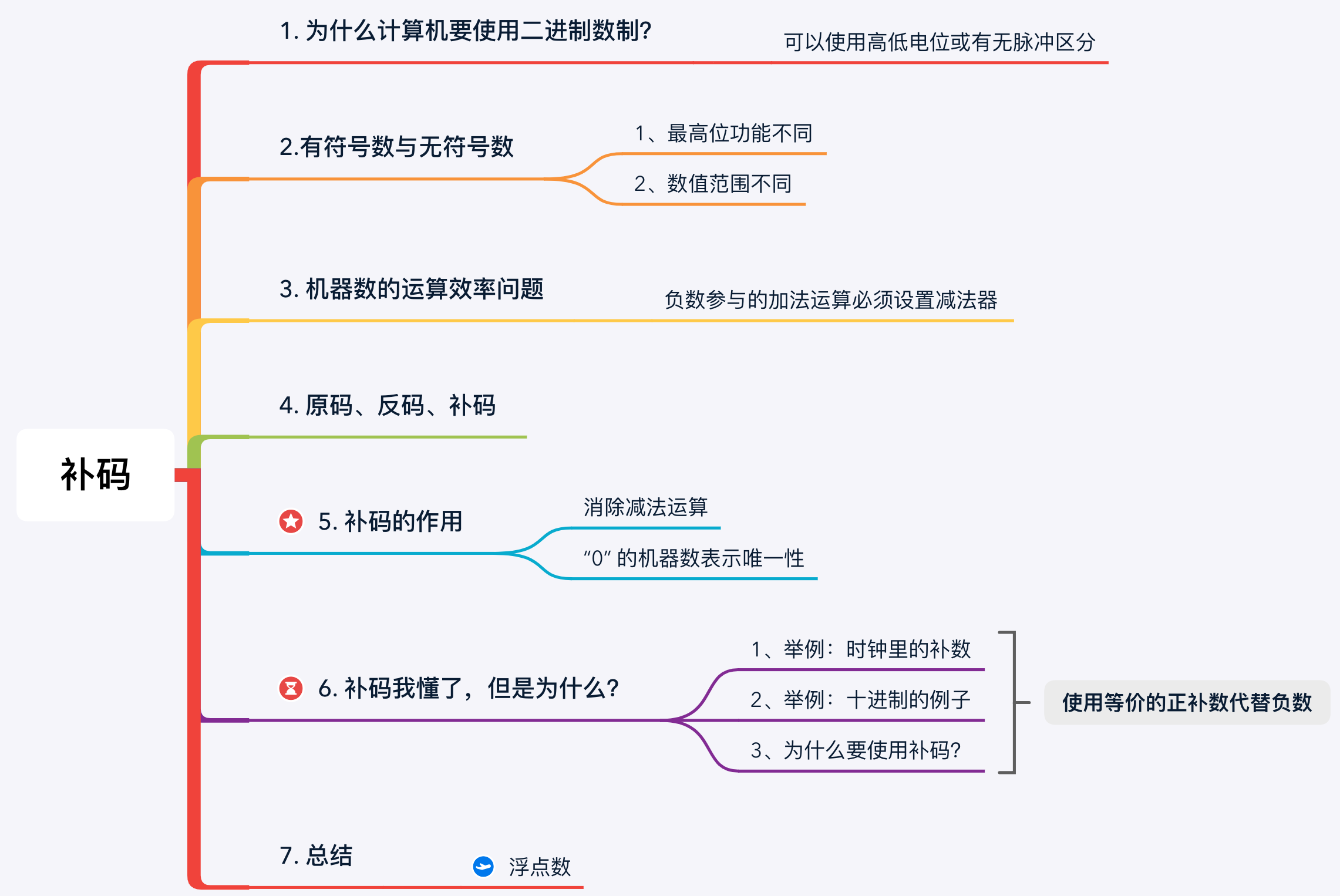
1. 為什麼計算機要使用二進位制數制？

所謂數制其實就是一種 「計數的進位方式」。

常見的數制有十進位制、二進位制、八進位制和十六進位制：

  • 十進位制是我們日常生活中最熟悉的進位方式，它一共有 0、1、2、3、4、5、6、7、8 和 9 十個符號。在計數的過程中，當某一位滿 10 時，就需要向它臨近的高位進一，即逢十進一；

  • 二進位制是程式設計師更熟悉的進位方式，也是隨著計算機的誕生而發展起來的，它只有 0 和 1 兩個符號。在計數的過程中，當某一位滿 2 時，就需要向它臨近的高位進一，即逢二進一；

  • 八進位制和十六進位制同理。

那麼，為什麼計算機要使用二進位制數制，而不是人類更熟悉的十進位制呢？其原因在於二進位制只有兩種狀態，製造只有 2 個穩定狀態的電子元器件可以使用高低電位或有無脈衝區分，而相比於具備多個狀態的電子元器件會更加穩定可靠。

2.有符號數與無符號數

在計算機中會區分有符號數和無符號數，無符號數不需要考慮符號，可以將數位編碼中的每一位都用來存放數值。有符號數需要考慮正負性，然而計算機是無法識別符號的 「正+」 或 「負-」 標誌的，那怎麼辦呢？

好在我們發現 「正 / 負」 是兩種截然不同的狀態，正好可以對映到計算機能夠理解的 「0 / 1」 上。因此，我們可以直接 「將符號數位化」，將 「正+」 數位化為 「0」，將 「負-」 數位化為 「1」，並將數位化後的符號和數值共同組成數位編碼。

另外，為了計算方便，我們額外再規定將 「符號位」 放在數位編碼的 「最高位」。例如，+1110 和 -1110 用 8 位二進位制表示就是：

  • 0000, 1110（符號作為編碼的一部分，最高位 0 表示正數）
  • 1000, 1110（符號作為編碼的一部分，最高位 1 表示負數）

從中我們也可以看出無符號數和有符號數的區別：

  • 1、最高位功能不同： 無符號數的編碼中的每一位都可以用來存放數值資訊，而有符號數需要在編碼的最高位留出一位符號位；

  • 2、數值範圍不同： 相同位數下有符號數和無符號數表示的數值範圍不同。以 16 位數為例，無符號數可以表示 0~65536，而有符號數可以表示 -32768~32768。

提示： 無符號數和有符號數表示的數值範圍大小是一樣大的，n 位二進位制最多隻能表示 $2^n$ 個資訊量，這是無法被突破的。

3. 機器數的運算效率問題

在計算機中，我們會把帶 「正 / 負」 符號的數稱為真值（True Value），而把符號化後的數稱為機器數（Computer Number)。

機器數才是數位在計算機中的二進位制表示。 例如在前面的數位中， +1110 是真值，而 0000, 1110 是機器數。新的問題來了：將符號數位化後的機器數，在運算的過程中符號位是否與數值參與運算，又應該如何運算呢？

我們先舉幾個加法運算的例子：

  • 兩個正數相加：
0000, 1110 + 0000, 0001 = 0000, 1111 // 14 + 1 = 15 正確
^            ^            ^
符號位        符號位        符號位
  • 兩個負數相加：
1000, 1110 + 1000, 0001 = 0000, 1111 // (-14) + (-1) = 15 錯誤
^            ^            ^
符號位        符號位        符號位（最高位的 1 溢位）
  • 正負數相加：
0000, 1110 + 1000, 0001 = 1001, 1111 // 14 + (-1) = -15 錯誤
^            ^            ^
符號位        符號位        符號位

可以看到，在對機器數進行 「按位元加法」 運算時，只有兩個正數的加法運算的結果是正確的，而包含負數的加法運算的結果卻是錯誤的，會出現 -14 - 1 = 15 和 14 - 1 = -15 這種錯誤結果。

所以，帶負數的加法運算就不能使用常規的按位元加法運算了，需要做特殊處理：

  • 兩個正數相加：

    • 直接做按位元加法。

  • 兩個負數相加：

    • 1、用較大的絕對值 + 較小的絕對值（加法運算）；
    • 2、最終結果的符號為負。

  • 正負數相加：

    • 1、判斷兩個數的絕對值大小（數值部分）；
    • 2、用較大的絕對值 - 較小的絕對值（減法運算）；
    • 3、最終結果的符號取絕對值較大數的符號。

哇