深度學習-第三章概率與資訊理論

前言
- 概率論學科定義
- 概率與資訊理論在人工智慧領域的應用
3.1，為什麼要使用概率論
3.2，隨機變數
3.3，概率分佈
- 3.3.1，離散型變數和概率質量函數
- 3.3.2，連續型變數和概率密度分佈函數
3.4，邊緣概率
3.5，條件概率
- 3.5.1，條件概率的鏈式法則
- 3.6，獨立性和條件獨立性
3.7，條件概率、聯合概率和邊緣概率總結
3.8，期望、方差和協方差
3.9，常用概率分佈
3.10，常用函數的有用性質
3.11，貝葉斯定理
- 3.11.1，貝葉斯定理公式
- 3.11.2，貝葉斯理論與概率密度函數
3.12，連續型變數的技術細節
3.13，資訊理論-相對熵和交叉熵
3.14，結構化概率模型
參考資料

本文首發於 github。最新版以 github 為主。如果看完文章有所收穫，一定要先點贊後收藏。畢竟，贈人玫瑰，手有餘香。
本文內容大多來自《深度學習》（花書）第三章概率與資訊理論。目錄的生成是參考此篇文章。

前言

概率論學科定義

概率論是用於表示不確定性宣告的數學框架。它不僅提供了量化不確定性的方法，也提供了用於匯出新的不確定性宣告（statement）的公理。概率論的知識在機器學習和深度學習領域都有廣泛應用，是學習這兩門學科的基礎。

概率與資訊理論在人工智慧領域的應用

在人工智慧領域，概率論主要有兩種用途。

首先，概率定律告訴我們 AI 系統應該如何推理，基於此我們設計一些演演算法來計算或者估算由概率論匯出的表示式。
其次，我們可以用概率和統計從理論上分析我們提出的 AI 系統的行為。

雖然概率論允許我們在存在不確定性的情況下做出不確定的陳述和推理，但資訊理論允許我們量化概率分佈中不確定性的數量。

3.1，為什麼要使用概率論

這是因為機器學習必須始終處理不確定的量，有時可能還需要處理隨機（非確定性）的量，這裡的不確定性和隨機性可能來自多個方面。而使用使用概率論來量化不確定性的論據，是來源於 20 世紀 80 年代的 Pearl (1988) 的工作。

不確定性有三種可能的來源:

被建模系統內在的隨機性。
不完全觀測。
不完全建模：使用了一些必須捨棄某些觀測資訊的模型。

3.2，隨機變數

隨機變數（random variable）是可以隨機地取不同值的變數，它可以是離散或者連續的。

離散隨機變數擁有有限或者可數無限多的狀態。注意這些狀態不一定非要是整數; 它們也可能只是一些被命名的狀態而沒有數值。連續隨機變數伴隨著實數值。注意，隨機變數只是對可能狀態的描述；它必須與指定這些狀態中的每一個的可能性的概率分佈相結合。

我們通常用無格式字型 (plain typeface) 中的小寫字母來表示隨機變數本身，而用手寫體中的小寫字母來表示隨機變數能夠取到的值。例如， $x_1$ 和 $x_2$ 都是隨機變數 $\textrm{x}$ 可能的取值。對於向量值變數，我們會將隨機變數寫成 $\mathbf{x}$，它的一個可能取值為 $\boldsymbol{x}$。

中文維基百科用 $X$ 表示隨機變數，用 $f_{X}(x)$ 表示概率密度函數，本文筆記，不同小節內容兩者混用。

3.3，概率分佈

概率分佈（probability distribution）是用來描述隨機變數或一簇隨機變數在每一個可能取到的狀態的可能性大小。

如果狹義地講，它是指隨機變數的概率分佈函數。具有相同概率分佈函數的隨機變數一定是相同分佈的。連續型和離散型隨機變數的概率分佈描述方式是不同的。

3.3.1，離散型變數和概率質量函數

離散型變數的概率分佈可以用概率質量函數（probability mass function, PMF，也稱概率密度函數）來描述。我們通常用大寫字母 $P$ 來表示概率質量函數，用 $\textrm{x} \sim P(\textrm{x})$ 表示隨機變數 $\textrm{x}$ 遵循的分佈。

雖然通常每一個隨機變數都會有一個不同的概率質量函數，但是概率質量函數也可以同時作用於多個隨機變數，這種多個變數的概率分佈被稱為聯合概率分佈（joint probability distribution）。 $P(\textrm{x} = x, \textrm{y} = y)$ 表示 $\textrm{x} = x$ 和 $\textrm{y} = y$ 同時發生的概率，有時也可簡寫為 $P(x，y)$。

如果一個函數 $P$ 是隨機變數 $\textrm{x}$ 的 PMF，必須滿足以下條件：

$P$ 的定義域必須是 $\textrm{x}$ 所有可能狀態的集合。
$\forall x \in \textrm{x}, 0 \leq P(x)\leq 1$。不可能發生的事件概率為 0，能夠確保一定發生的事件概率為 1。
$\sum_{x \in \textrm{x}}P(x)=1$，歸一化（normalized）。

常見的離散概率分佈族有：

伯努利分佈
二項分佈：一般用二項分佈來計算概率的前提是，每次抽出樣品後再放回去，並且只能有兩種試驗結果，比如黑球或紅球，正品或次品等。
幾何分佈
Poisson 分佈（泊松分佈）：Poisson 近似是二項分佈的一種極限形式。
離散均勻分佈：即對於隨機變數 $\textrm{x}$，因為其是均勻分佈(uniform distribution)，所以它的 PMF 為 $P(\textrm{x}=x_{i}) = \frac{1}{k}$，同時 $\sum_{i}P(\textrm{x} = x_{i}) = \sum_{i}\frac{1}{k} = \frac{k}{k} = 1$。

3.3.2，連續型變數和概率密度分佈函數

連續型隨機變數的概率分佈可以用概率密度函數（probability desity function, PDF）來描述。

通常用小寫字母 $p$ 來表示隨機變數 $\textrm{x}$ 的概率密度函數 PDF，其必須滿足以下條件：

$p$ 的定義域必須是 $\textrm{x}$ 所有可能狀態的集合。
$\forall x \in \textrm{x}, p(x)\geq 0$。注意，並不要求 $p(x)\leq 1$。
$\int p(x)dx=1$。

概率密度函數 $p(x)$ 給出的是落在面積為 $\delta x$ 的無限小的區域內的概率為 $p(x)\delta x$。

因此，我們可以對概率密度函數求積分來獲得點集的真實概率質量。特別地，$x$ 落在集合 $\mathbb{S}$ 中的概率可以通過 $p(x)$ 對這個集合求積分來得到。在單變數的例子中，$x$ 落在區間 $[a,b]$ 的概率是 $\int_{[a,b]}p(x)dx$。

常見的連續概率分佈族有：

均勻分佈
正態分佈：連續型隨機變數的概率密度函數如下所示。其密度函數的曲線呈對稱鐘形，因此又被稱之為鐘形曲線，其中$\mu$ 是平均值，$\sigma$ 是標準差。正態分佈是一種理想分佈。$${f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{\left(-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}\right)}}$$
伽瑪分佈
指數分佈

3.4，邊緣概率

邊緣概率好像應用並不多，所以這裡理解定義和概念即可。
邊緣概率的通俗理解描述，來源於數學篇 - 概率之聯合概率、條件概率、邊緣概率和貝葉斯法則(筆記)。

有時候，我們知道了一組變數的聯合概率分佈，但想要了解其中一個子集的概率分佈。這種定義在子集上的概率分佈被稱為邊緣概率分佈(marginal probability distribution)。

對於離散型隨機變數 $\textrm{x}$ 和 $\textrm{y}$，知道 $P(\textrm{x}, \textrm{y})$，可以依據下面的求和法則（sum rule）來計算邊緣概率 $P(\textrm{x})$：

\[\forall x \in \textrm{x},P(\textrm{x}=x)=\sum_{y}P(\textrm{x}=x, \textrm{y}=y) \]

「邊緣概率」的名稱來源於手算邊緣概率的計算過程。當 $P(x,y)$ 的每個值被寫在由每行表示不同的 $x$ 值，每列表示不同的 $y$ 值形成的網格中時，對網格中的每行求和是很自然的事情，然後將求和的結果 $P(x)$ 寫在每行右邊的紙的邊緣處。

連續性變數的邊緣概率則用積分代替求和：

\[p(x) = \int p(x,y)dy \]

3.5，條件概率

條件概率（conditional probability）就是事件 A 在事件 B 發生的條件下發生的概率，表示為 $P(A|B)$。

設 $A$ 與 $B$ 為樣本空間 Ω 中的兩個事件，其中 $P(B) > 0$。那麼在事件 $B$ 發生的條件下，事件 $A$ 發生的條件概率為：

\[P(A|B)={\frac {P(A\cap B)}{P(B)}} \]

花書中期望的條件概率定義（表示式不一樣，但意義是一樣的，維基百科的定義更容易理解名字意義，花書中的公式更多的是從數學中表達）:

將給定 $\textrm{x} = x$ 時， $\textrm{y} = y$ 發生的條件概率記為 $P(\textrm{y} = y|\textrm{x} = x)$，這個條件概率的計算公式如下：

\[P(\textrm{y}=y|\textrm{x}=x)=\frac{P(\textrm{y}=y, \textrm{x}=x)}{P(\textrm{x}=x)} \]
條件概率只在 $P(\textrm{x}=x)\geq 0$ 時有定義，即不能計算以從未發生的事件為條件的條件概率。

3.5.1，條件概率的鏈式法則

任何多維隨機變數的聯合概率分佈，都可以分解成只有一個變數的條件概率相乘的形式，這個規則被稱為概率的鏈式法則（chain rule）。條件概率的鏈式法則如下:

\[\begin{aligned} P(a,b,c) = P(a|b,c)P(b,c) \\ P(b,c) = P(b|c)P(c) \\ P(a,b,c) = P(s|b,c)P(b|c)P(c) \end{aligned} \]

3.6，獨立性和條件獨立性

兩個隨機變數 $\textrm{x}$ 和 $\textrm{y}$，如果它們的概率分佈可以表示成兩個因子的乘積形式，並且一個因子只包含 $\textrm{x}$ 另一個因子只包含 $\textrm{y}$，我們就稱這兩個隨機變數是相互獨立的（independent）：

\[\forall x \in \textrm{x},y \in \textrm{y},p(\textrm{x}=x, \textrm{y}=y)=p(\textrm{x}=x)\cdot p(\textrm{y}=y) \]

兩個相互獨立的隨機變數同時發生的概率可以通過各自發生的概率的乘積得到。

如果關於 $x$ 和 $y$ 的條件概率分佈對於 $z$ 的每一個值都可以寫成乘積的形式，那麼這兩個隨機變數 $x$ 和 $y$ 在給定隨機變數 $z$ 時是條件獨立的(conditionally independent):

\[\forall x \in ,y \in \textrm{y},z \in \textrm{z}, p(\textrm{x}=x, \textrm{y}=y|z \in \textrm{z})= p(\textrm{x}=x|z \in \textrm{z})\cdot p(\textrm{y}=y|z \in \textrm{z}) \]

採用一種簡化形式來表示獨立性和條件獨立性: $\textrm{x}\perp \textrm{y}$ 表示 $\textrm{x}$ 和 $\textrm{y}$ 相互獨立，$\textrm{x}\perp \textrm{y}|\textrm{z}$ 表示 $\textrm{x}$ 和 $\textrm{y}$ 在給定 $\textrm{z}$ 時條件獨立。

3.7，條件概率、聯合概率和邊緣概率總結

條件概率（conditional probability）就是事件 A 在事件 B 發生的條件下發生的概率。條件概率表示為 $P(A|B)$，讀作「A 在 B 發生的條件下發生的概率」。
聯合概率表示兩個事件共同發生的概率。A 與 B 的聯合概率表示為 $P(A\cap B)$ 或者 $P(A,B)$ 或者 $P(AB)$。
僅與單個隨機變數有關的概率稱為邊緣概率。

3.8，期望、方差和協方差

為了便於理解，本章中的數學公式描述採用中文維基百科中的定義。

在概率分佈中，期望值和方差或標準差是一種分佈的重要特徵，期望、數學期望、均值都是一個意思。統計中的方差（樣本方差）是每個樣本值與全體樣本值的平均數之差的平方值的平均數，其意義和概率分佈中的方差是不一樣的。

3.8.1，期望

在概率論和統計學中，一個離散性隨機變數的期望值（或數學期望，亦簡稱期望，物理學中稱為期待值）是試驗中每次可能的結果乘以其結果概率的總和。換句話說，期望值像是隨機試驗在同樣的機會下重複多次，所有那些可能狀態平均的結果，也可理解為該變數輸出值的加權平均。

期望數學定義

如果 $X$ 是在概率空間 $(\Omega ,F,P)$ 中的隨機變數，那麼它的期望值 $\operatorname{E}(X)$ 的定義是：

\[\operatorname {E}(X)=\int_{\Omega }X {d}P \]

並不是每一個隨機變數都有期望值的，因為有的時候上述積分不存在。如果兩個隨機變數的分佈相同，則它們的期望值也相同。

1，如果 $X$ 是離散的隨機變數，輸出值為 $x_{1},x_{2},\ldots x_{1},x_{2},\ldots$，和輸出值相應的概率為 ${\displaystyle p_{1},p_{2},\ldots }p_{1},p_{2},\ldots$（概率和為 1）。

若級數 $\sum_{i}p_{i}x_{i}$ 絕對收斂，那麼期望值 $\operatorname {E}(X)$ 是一個無限數列的和。

\[\operatorname {E}(X)=\sum_{i}p_{i}x_{i} \]

2，如果 $X$ 是連續的隨機變數，且存在一個相應的概率密度函數 $f(x)$，若積分 $\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x$ 絕對收斂，那麼 $X$ 的期望值可以計算為：

\[\operatorname {E} (X)=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x \]

雖然是針對於連續的隨機變數的，但與離散隨機變數的期望值的計算演演算法卻同出一轍，由於輸出值是連續的，所以只是把求和改成了積分。

期望值 $E$ 是線性函數:

\[\operatorname {E}(aX+bY)=a\operatorname {E}(X)+b\operatorname {E}(Y) \]

$X$ 和 $Y$ 為在同一概率空間的兩個隨機變數（可以獨立或者非獨立），$a$ 和 $b$ 為任意實數。

花書中期望的數學定義（表示式不一樣，但意義是一樣的）:

1，某個函數 $f(x)$ 相對於概率分佈 $P(x)$ 的期望或期望值是當從 $P$ 中抽取 $x$ 時 $f$ 所取的平均或平均值。對於離散型隨機變數，期望可以通過求和得到：

\[\mathbb{E}_{\textrm{x}\sim P}[f(x)] = \sum_{x} P(x)f(x) \]
2，對於連續型隨機變數可以通過求積分得到：

\[\mathbb {E}_{\textrm{x}\sim p}[f(x)] = \int p(x)f(x)dx \]

期望應用

在統計學中，估算變數的期望值時，經常用到的方法是重複測量此變數的值，再用所得資料的平均值來估計此變數的期望值。
在概率分佈中，期望值和方差或標準差是一種分佈的重要特徵。

3.8.2，方差

在概率論和統計學中，方差（英語：variance）又稱變異數、變方，描述的是一個隨機變數的離散程度，即該變數離其期望值的距離，是隨機變數與其總體均值或樣本均值的離差的平方的期望值。

方差差是標準差的平方、分佈的二階矩，以及隨機變數與其自身的協方差，其常用的符號表示有 $\sigma^2$、$s^2$、$\operatorname {Var} (X)$、$\displaystyle V(X)$，以及 $\displaystyle \mathbb {V} (X)$。

方差作為離散度量的優點是，它比其他離散度量（如平均差）更易於代數運算，但缺點是它與隨機變數的單位不同，而標準差則單位相同，這就是計算完成後通常採用標準差來衡量離散程度的原因。

方差的正平方根稱為該隨機變數的標準差。

有兩個不同的概念都被稱為「方差」。一種如上所述，是理論概率分佈的方差。而另一種方差是一組觀測值的特徵，分別是總體方差（所有可能的觀測）和樣本方差（總體的一個子集）。

方差數學定義

設 $X$ 為服從分佈 $F$ 的隨機變數，如果 $\operatorname{E}[X]$ 是隨機變數 $X$ 的期望值（均值 $\mu=\operatorname{E}[X]$），則隨機變數 $X$ 或者分佈 $F$ 的方差為 $X$ 的離差平方的期望值:

\[\operatorname{E}(X) = \operatorname{E}[(X - \mu)]^2 = \operatorname{E}[X - \operatorname{E}(X)]^2 \]

方差的表示式可展開如下：

\[{\begin{aligned}\operatorname {Var} (X) &=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt] &=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt] &=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt] &=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}} \]

也就是說，$X$ 的方差等於 $X$ 平方的均值減去 $X$ 均值的平方。

總體方差數學定義

一般而言，一個有限的容量為 $N$、元素的值為 $x_{i}$ 的總體的總體方差為：

\[{\begin{aligned} \sigma ^{2}&={\frac {1}{N}}\sum _{i=1}^{N}\left(x_{i}-\mu \right)^{2} \end{aligned}} \]

花書中方差的定義: 方差（variance）衡量的是當我們對 $x$ 依據它的概率分佈進行取樣時，隨機變數 $\textrm{x}$ 的函數值會呈現多大的差異，或者說一個隨機變數的方差描述的是它的離散程度，也就是該變數離其期望值的距離。方差定義如下：

\[Var(f(x)) = \mathbb{E}[(f(x) - \mathbb{E}[f(x)])^2] \]

3.8.3，期望與方差的運算性質

期望與方差運算性質如下:

來源: 知乎文章-【AP統計】期望E(X)與方差Var(X)。

3.8.4，協方差

協方差也叫共變異數（英語：Covariance），在概率論與統計學中用於衡量兩個隨機變數的聯合變化程度。

協方差數學定義

期望值分別為 $\operatorname E(X)=\mu$ 與 $\operatorname E(Y)=\nu$ 的兩個具有有限二階矩的實數隨機變數 $X$ 與 $Y$ 之間的協方差定義為：

\[\operatorname {cov} (X,Y)=\operatorname {E} ((X-\mu )(Y-\nu ))=\operatorname {E} (X\cdot Y)-\mu \nu \]

協方差表示的是兩個變數的總體的誤差，這與只表示一個變數誤差的方差不同。

協方差的絕對值如果很大則意味著變數值變化很大並且它們同時距離各自的均值很遠。如果協方差是正的，那麼兩個變數都傾向於同時取得相對較大的值。如果協方差是負的，那麼其中一個變數傾向於取得相對較大的值的同時，另一個變數傾向於取得相對較小的值，反之亦然。其他的衡量指標如相關係數(correlation)將每個變量的貢獻歸一化，為了只衡量變數的相關性而不受各個變數尺度大小的影響。

3.9，常用概率分佈

下表列出了一些常用概率分佈的方差。

3.9.1，伯努利分佈

伯努利分佈（英語：Bernoulli distribution），又名兩點分佈或者 0-1 分佈，是一個離散型概率分佈，為紀念瑞士科學家雅各布·伯努利而命名。若伯努利試驗成功，則伯努利隨機變數取值為 1。若伯努利試驗失敗，則伯努利隨機變數取值為 0。記其成功概率為 $0\leq p\leq 1$，失敗概率為 $q = 1-p$。其有如下性質:

其概率質量函數為:

\[f_{X}(x) = p^{x}(1-p)^{1-x} = \left\{\begin{matrix} p \quad if \;x = 1 \\ 1-p \quad if \; x = 0 \end{matrix}\right.\]

其期望值為:

\[\operatorname {E} [X] = \sum_{i=0}^{1} x_{i}f_X(x) = 0 + p = p \]

其方差為:

\[\begin{aligned} Var[X] &= \sum_{i=0}^{1} (x_{i}-\operatorname {E} [X])^2f_{X}(x) \\ &= (0-P)^2(1-P) + (1-P)^2P \\ &= p(1-p) \\ &= p\cdot q \\ \end{aligned}\]

3.9.2，Multinoulli 分佈

Multinoulli 分佈(多項式分佈，也叫範疇分佈 categorical dis- tribution)是一種離散概率分佈，它描述了隨機變數的可能結果，該隨機變數可以採用 $k$ 個可能類別之一，概率為每個類別分別指定，其中 $k$ 是一個有限值。

3.9.3，高斯分佈

有幾種不同的方法用來說明一個隨機變數。最直觀的方法是概率密度函數，這種方法能夠表示隨機變數每個取值有多大的可能性。

高斯分佈 Gaussian distribution（也稱正態分佈 Normal distribution）是一個非常常見的連續概率分佈。高斯分佈在統計學上十分重要，經常用在自然和社會科學來代表一個不確定的隨機變數。

若隨機變數 $X$ 服從一個位置引數為 $\mu$ 、尺度引數為 $\sigma$ 的正態分佈，記為：

\[X \sim N(\mu,\sigma^2) \]

則其概率密度函數為 $$f(x;\mu, \sigma) = \frac {1}{\sigma {\sqrt {2\pi }}};e^{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}}$$

正態分佈的數學期望值 $\mu$ 等於位置引數，決定了分佈的位置；其方差 $\sigma^2$ 的開平方或標準差 $\sigma$ 等於尺度引數，決定了分佈的幅度。

正態分佈概率密度函數曲線呈鐘形，也稱之為鐘形曲線（類似於寺廟裡的大鐘，因此得名）。我們通常所說的標準常態分佈是位置引數 $\mu = 0$，尺度引數 $\sigma ^{2} = 1$ 的正態分佈（見右圖中紅色曲線）。

採用正態分佈在很多應用中都是一個明智的選擇。當我們由於缺乏關於某個實數上分佈的先驗知識而不知道該選擇怎樣的形式時，正態分佈是預設的比較好的選擇，其中有兩個原因。

第一，我們想要建模的很多分佈的真實情況是比較接近正態分佈的。
第二，在具有相同方差的所有可能的概率分佈中，正態分佈在實數上具有最的不確定性。因此，我們可以認為正態分佈是對模型加入的先驗知識量最少的分佈。

3.9.4，指數分佈和 Laplace 分佈

在概率論和統計學中，指數分佈（Exponential distribution）是一種連續概率分佈，表示一個在 $x = 0$ 點處取得邊界點 (sharp point) 的分佈，其使用指示函數(indicator function) $1_{x\geq0}$ 來使得當 $x$ 取負值時的概率為零。指數分佈可以等同於形狀母數 $\alpha$為 $1$的伽瑪分佈。

指數分佈可以用來表示獨立隨機事件發生的時間間隔，比如旅客進入機場的時間間隔、電話打進客服中心的時間間隔等。

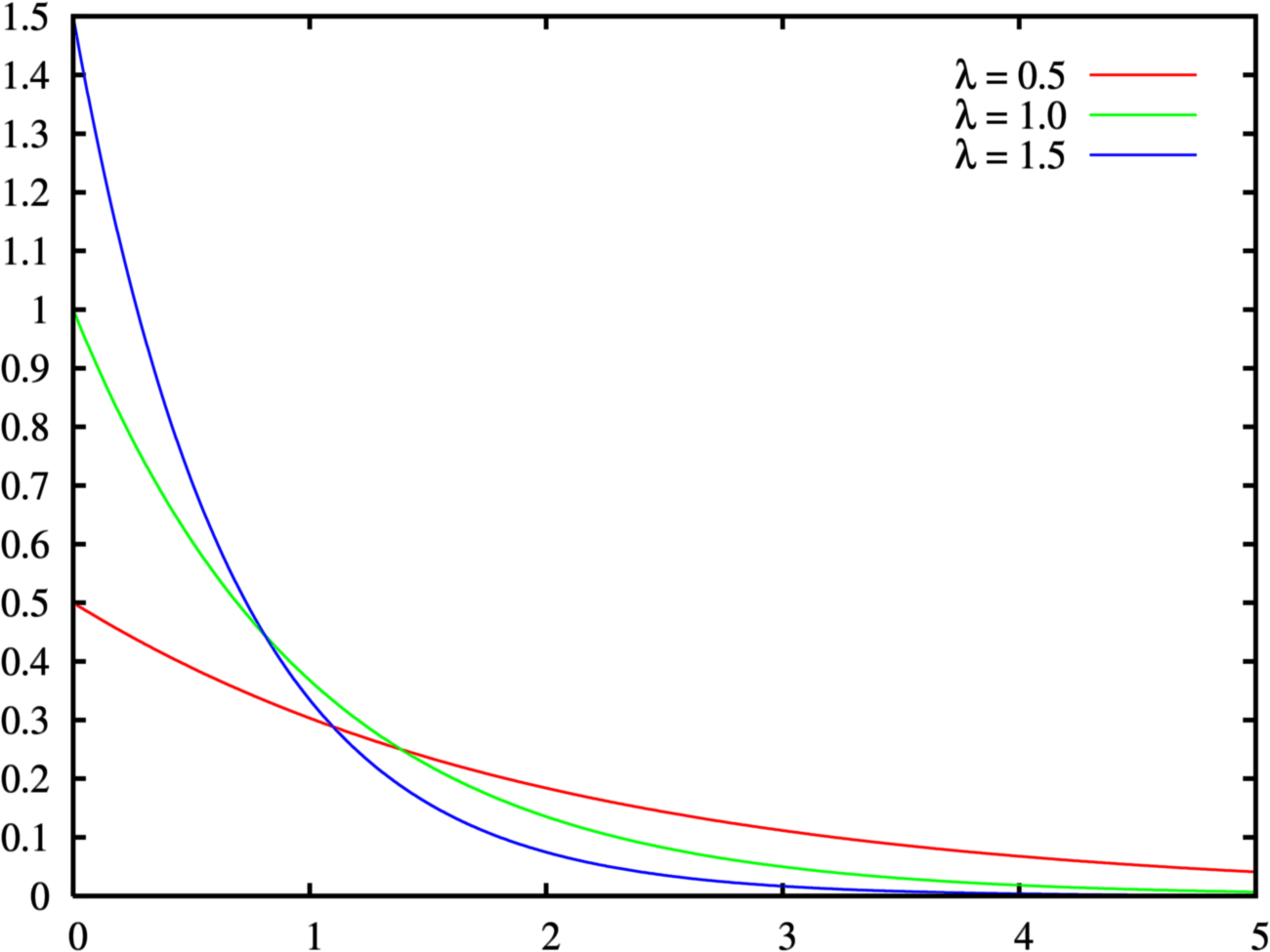
若隨機變數 $X$ 服從母數為 $\lambda$ 或 $\beta$ 的指數分佈，則記作

$X\sim {\text{Exp}}(\lambda )$ 或 $X\sim {\text{Exp}}(\beta )$

兩者意義相同，只是 $\lambda$ 與 $\beta$ 互為倒數關係。指數分佈的概率密度函數為：

\[f(x;{\color {Red}\lambda })=\left\{{\begin{matrix}{\color {Red}\lambda }e^{-{\color {Red}\lambda }x}&x\geq 0,\\0&,\;x<0.\end{matrix}}\right. \]

指數分配概率密度函數曲線如下所示。

3.10，常用函數的有用性質

深度學習中的概率分佈有一些經常出現的函數，比如 logistic sigmoid 函數:

\[\sigma(x) = \frac{1}{1+exp(-x)} \]

logistic sigmoid 函數通常用來產生伯努利分佈的引數 $p$，因為它的範圍是 $(0, 1)$，位於 $p$ 引數值的有效範圍內。下圖 3.3 給出了 sigmoid 函數的圖示。從圖中可以明顯看出，sigmoid 函數在變數取絕對值非常大的正值或負值時會出現飽和(saturate)現象，意味著函數會變得很平，並且對輸入的微小改變會變得不敏感。

sigmoid 函數的一些性質在後續學習 BP 演演算法等內容時會很有用，我們需要牢記：

\[\begin{align} \sigma(x) &= \frac{exp(x)}{exp(x)+exp(0)} \nonumber \\ \frac{d}{dx}\sigma(x) &= \sigma(x)(1 - \sigma(x)) \nonumber \\ 1 - \sigma(x) &= \sigma(-x) \nonumber \\ \end{align} \]

3.11，貝葉斯定理

本小節只是簡單介紹基本概念和公式，更全面和深入的理解建議看《機器學習》書籍。

貝葉斯定理（英語：Bayes' theorem）是概率論中的一個定理，描述在已知一些條件下，某事件的發生概率。比如，如果已知某種健康問題與壽命有關，使用貝葉斯定理則可以通過得知某人年齡，來更加準確地計算出某人有某種健康問題的概率。

通常，事件 A 在事件 B 已發生的條件下發生的概率，與事件 B 在事件 A 已發生的條件下發生的概率是不一樣的。但是，這兩者是有確定的關係的，貝葉斯定理就是這種關係的陳述。貝葉斯公式的一個用途，即透過已知的三個概率而推出第四個概率。貝葉斯定理跟隨機變數的條件概率以及邊際概率分佈有關。

作為一個普遍的原理，貝葉斯定理對於所有概率的解釋是有效的。這一定理的主要應用為貝葉斯推斷，是推論統計學中的一種推斷法。這一定理名稱來自於托馬斯·貝葉斯。

來源中文維基百科-貝葉斯定理

3.11.1，貝葉斯定理公式

貝葉斯定理是關於隨機事件 A 和 B 的條件概率的一則定理。

\[P(A\mid B)={\frac {P(A)P(B\mid A)}{P(B)}} \]

其中 A 以及 B 為隨機事件，且 $P(B)$ 不為零。$P(A\mid B)$ 是指在事件 B 發生的情況下事件 A 發生的概率。

在貝葉斯定理中，每個名詞都有約定俗成的名稱：

$P(A\mid B)$ 是已知 B 發生後，A 的條件概率。也稱作 A 的事後概率。
$P(A)$ 是 A 的先驗概率（或邊緣概率）。其不考慮任何 B 方面的因素。
$P(B\mid A)$ 是已知 A 發生後，B 的條件概率。也可稱為 B 的後驗概率。某些文獻又稱其為在特定 B 時，A 的似然性，因為 $P(B\mid A)=L(A\mid B)$。
$P(B)$是 B 的先驗概率。

3.11.2，貝葉斯理論與概率密度函數

貝葉斯理論亦可用於概率分佈，貝葉斯理論與概率密度的關係是由求極限的方式建立：

\[P(\textrm{x}|\textrm{y}) = \frac{P(\textrm{x})P(\textrm{y}|\textrm{x})}{P(\textrm{y})} \]

注意到 $P(y)$ 出現在上面的公式中，它通常使用 $P(\textrm{y}) = \sum_{x} P(\textrm{y}|x)P(x)$ 來計算所以我們並不需要事先知道 $P(\textrm{y})$ 的資訊。

中文維基百科中貝葉斯理論與概率密度關係定義:

\[f(x|y)={\frac {f(x,y)}{f(y)}}={\frac {f(y|x)\,f(x)}{f(y)}} \]

3.12，連續型變數的技術細節

連續型隨機變數和概率密度函數的深入理解需要用到數學分支測度論(measure theory)的相關內容來擴充套件概率論，測度論超出了本書範疇。

原書中有測度論的簡要介紹，本筆記不做記錄和摘抄，感興趣的可以閱讀原書。

3.13，資訊理論-相對熵和交叉熵

資訊理論是應用數學、電子學和電腦科學的一個分支，早期備用在無線通訊領域。在深度學習中，主要是使用資訊理論的一些關鍵思想來表徵(characterize)概率分佈或者量化概率分佈之間的相似性。

資訊理論的基本想法是一個不太可能的事件居然發生了，要比一個非常可能的事件發生，能提供更多的資訊。

自資訊只處理單個的輸出。我們可以用夏農熵(Shannon entropy)來對整個概率分佈中的不確定性總量進行量化:

\[H(P) = H(\textrm{x}) = E_{x∼P}[I(x)] = −E_{x∼P}[log P(x)] \]

換句話說，一個概率分佈的夏農熵是指遵循這個分佈的事件所產生的期望資訊總量。

如果我們對於同一個隨機變數 $\textrm{x}$ 有兩個單獨的概率分佈 $P(x)$ 和 $Q(x)$，則可以用 KL 散度（ Kullback-Leibler (KL) divergence，也叫相對熵）來衡量這兩個概率分佈的差異：

\[D_{KL}(P\parallel Q) = \mathbb{E}_{\textrm{x}\sim p}\begin{bmatrix} log \frac{P(x)}{Q(x)} \end{bmatrix} = \mathbb{E}_{\textrm{x}\sim p}[log P(x) - log Q(x)]\]

KL 散度有很多有用的性質，最重要的是它是非負的。KL 散度為 0 當且僅當 $P$ 和 $Q$ 在離散型變數的情況下是相同的概率分佈，或者在連續型變數的情況下是「幾乎處處」相同的。

一個和 KL 散度密切聯絡的量是交叉熵(cross-entropy)$H(P, Q) = H(P) + D_{KL}(P||Q)$，其計算公式如下:

\[H(P, Q) = -\mathbb{E}_{\textrm{x}\sim p}log Q(x) \]

和 KL 散度相比，少了左邊一項，即熵 $H(P)$。可以看出，最小化 KL 散度（交叉熵）其實就是在最小化分佈之間的交叉熵（KL 散度）。

上式的寫法是在前面所學內容數學期望的基礎上給出的，還有一個寫法是《機器學習-周志華》書中附錄 C 中給出的公式，更為直觀理解：

\[KL(P\parallel Q) = \int_{-\infty }^{+\infty} p(x)log \frac{p(x)}{q(x)} dx \]
其中 $p(x)$ 和 $q(x)$ 分別為 $P$ 和 $Q$ 的概率密度函數。
這裡假設兩個分佈均為連續型概率分佈，對於離散型概率分佈，只需要將積分替換為對所有離散值遍歷求和。

KL 散度滿足非負性和不滿足對稱性。將上式展開可得：

\[\text{KL 散度} KL(P\parallel Q) = \int_{-\infty }^{+\infty}p(x)logp(x)dx - \int_{-\infty }^{+\infty}p(x) logq(x)dx = -H(P) + H(P,Q) \]
\[\text{交叉熵} H(P,Q) = \mathbb{E}_{\textrm{x}\sim p} log Q(x) = - \int_{-\infty }^{+\infty} p(x) logq(x)dx \]

其中，$H(P)$ 為熵（entropy），$H(P,Q)$ 為交叉熵（cross entropy）。

在資訊理論中，熵 $H(P)$ 表示對來自 $P$ 的隨機遍歷進行編碼所需的最小位元組數，而交叉熵 $H(P,Q)$ 表示使用 $Q$ 的編碼對來自 $P$ 的變數進行編碼所需的位元組數。因此 KL 散度可認為是使用基於 $Q$ 的編碼對來自 $P$ 的變數進行編碼所需的「額外位元組數」；顯然，額外位元組數非負，當且僅當 $P=Q$ 時額外位元組數為 0。

3.14，結構化概率模型

略

參考資料

https://zh.m.wikipedia.org/zh-hans/方差#
《深度學習》
《機器學習》