B-神經網路模型複雜度分析

• 前言
• 一，模型計算量分析
  • 折積層 FLOPs 計算
  • 全連線層的 FLOPs 計算
• 二，模型引數量分析
  • 折積層引數量
  • BN 層引數量
  • 全連線層引數量
• 三，模型記憶體存取代價計算
  • 折積層 MAC 計算
• 四，一些概念
  • 雙精度、單精度和半精度
  • 浮點計算能力
  • 硬體利用率(Utilization)
• 五，參考資料

前言

現階段的輕量級模型 MobileNet/ShuffleNet 系列、CSPNet、RepVGG、VoVNet 等都必須依賴於於具體的計算平臺（如 CPU/GPU/ASIC 等）才能更完美的發揮網路架構。

1，計算平臺主要有兩個指標：算力 $\pi $和 頻寬 $\beta $。

• 算力指的是計算平臺每秒完成的最大浮點運算次數，單位是 FLOPS
• 頻寬指的是計算平臺一次每秒最多能搬運多少資料（每秒能完成的記憶體交換量），單位是 Byte/s。

計算強度上限 \(I_{max}\)，上面兩個指標相除得到計算平臺的計算強度上限。它描述了單位記憶體交換最多用來進行多少次計算，單位是 FLOPs/Byte。

這裡所說的「記憶體」是廣義上的記憶體。對於 CPU 而言指的就是真正的記憶體（RAM）；而對於 GPU 則指的是視訊記憶體。

2，和計算平臺的兩個指標相呼應，模型也有兩個主要的反饋速度的間接指標：計算量 FLOPs 和訪存量 MAC。

• 計算量（FLOPs）：指的是輸入單個樣本（一張影象），模型完成一次前向傳播所發生的浮點運算次數，即模型的時間複雜度，單位是 FLOPs。
• 訪存量（MAC）：指的是輸入單個樣本（一張影象），模型完成一次前向傳播所發生的記憶體交換總量，即模型的空間複雜度，單位是 Byte，因為資料型別通常為 float32，所以需要乘以 4。CNN 網路中每個網路層 MAC 的計算分為讀輸入 feature map 大小、權重大小（DDR 讀）和寫輸出 feature map 大小（DDR 寫）三部分。
• 模型的計算強度 \(I\) ：\(I = \frac{FLOPs}{MAC}\)，即計算量除以訪存量後的值，表示此模型在計算過程中，每 Byte 記憶體交換到底用於進行多少次浮點運算。單位是 FLOPs/Byte。可以看到，模計算強度越大，其記憶體使用效率越高。
• 模型的理論效能 \(P\) ：我們最關心的指標，即模型在計算平臺上所能達到的每秒浮點運算次數（理論值）。單位是 FLOPS or FLOP/s。Roof-line Model 給出的就是計算這個指標的方法。

3，Roofline 模型講的是程式在計算平臺的算力和頻寬這兩個指標限制下，所能達到的理論效能上界，而不是實際達到的效能，因為實際計算過程中還有除算力和頻寬之外的其他重要因素，它們也會影響模型的實際效能，這是 Roofline Model 未考慮到的。例如矩陣乘法，會因為 cache 大小的限制、GEMM 實現的優劣等其他限制，導致你幾乎無法達到 Roofline 模型所定義的邊界（屋頂）。

所謂 「Roof-line」，指的就是由計算平臺的算力和頻寬上限這兩個引數所決定的「屋頂」形態，如下圖所示。

• 算力決定「屋頂」的高度（綠色線段）
• 頻寬決定「房檐」的斜率（紅色線段）

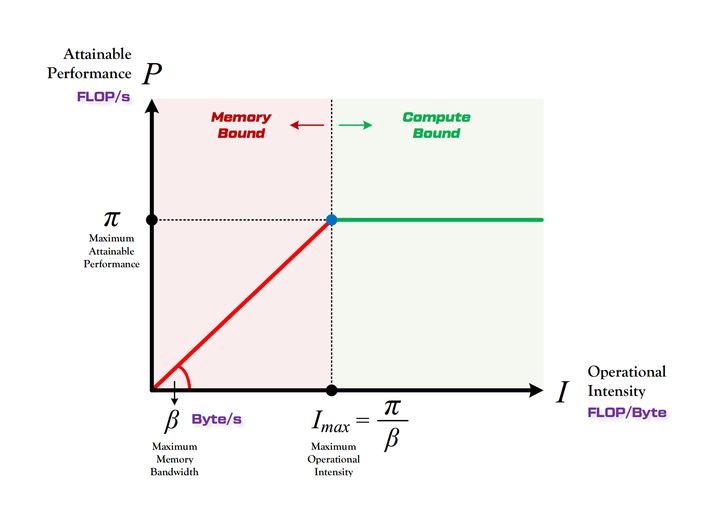
Roof-line 劃分出的兩個瓶頸區域定義如下：

個人感覺如果在給定計算平臺上做模型部署工作，因為晶片的算力已定，工程師能做的主要工作應該是提升頻寬。

一，模型計算量分析

終端裝置上執行深度學習演演算法需要考慮記憶體和算力的需求，因此需要進行模型複雜度分析，涉及到模型計算量（時間/計算複雜度）和模型引數量（空間複雜度）分析。

為了分析模型計算複雜度，一個廣泛採用的度量方式是模型推斷時浮點運算的次數 （FLOPs），即模型理論計算量，但是，它是一個間接的度量，是對我們真正關心的直接度量比如速度或者時延的一種近似估計。

本文的折積核尺寸假設為為一般情況，即正方形，長寬相等都為 K。

• FLOPs：floating point operations 指的是浮點運算次數,理解為計算量，可以用來衡量演演算法/模型時間的複雜度。
• FLOPS：（全部大寫）,Floating-point Operations Per Second，每秒所執行的浮點運算次數，理解為計算速度,是一個衡量硬體效能/模型速度的指標。
• MACCs：multiply-accumulate operations，乘-加操作次數，MACCs 大約是 FLOPs 的一半。將 \(w[0]*x[0] + ...\) 視為一個乘法累加或 1 個 MACC。

注意相同 FLOPs 的兩個模型其執行速度是會相差很多的，因為影響模型執行速度的兩個重要因素只通過 FLOPs 是考慮不到的，比如 MAC（Memory Access Cost）和網路並行度；二是具有相同 FLOPs 的模型在不同的平臺上可能執行速度不一樣。

注意，網上很多文章將 MACCs 與 MACC 概念搞混，我猜測可能是機器翻譯英文文章不準確的緣故，可以參考此連結瞭解更多。需要指出的是，現有很多硬體都將乘加運算作為一個單獨的指令。

折積層 FLOPs 計算

折積操作本質上是個線性運算，假設折積核大小相等且為 \(K\)。這裡給出的公式寫法是為了方便理解，大多數時候為了方便記憶，會寫成比如 \(MACCs = H \times W \times K^2 \times C_i \times C_o\)。

• \(FLOPs=(2\times C_i\times K^2-1)\times H\times W\times C_o\)（不考慮bias）
• \(FLOPs=(2\times C_i\times K^2)\times H\times W\times C_o\)（考慮bias）
• \(MACCs=(C_i\times K^2)\times H\times W\times C_o\)（考慮bias）

\(C_i\) 為輸入特徵圖通道數，\(K\) 為過折積核尺寸，\(H,W,C_o\) 為輸出特徵圖的高，寬和通道數。二維折積過程如下圖所示：

二維折積是一個相當簡單的操作：從折積核開始，這是一個小的權值矩陣。這個折積核在 2 維輸入資料上「滑動」，對當前輸入的部分元素進行矩陣乘法，然後將結果匯為單個輸出畫素。

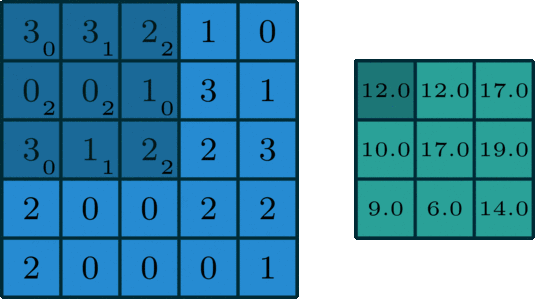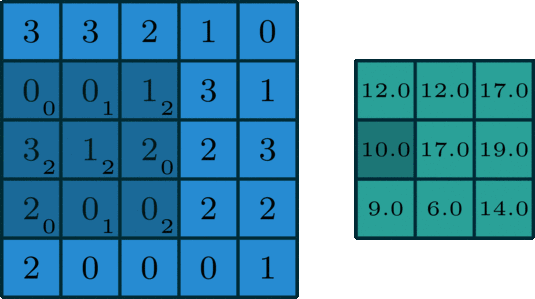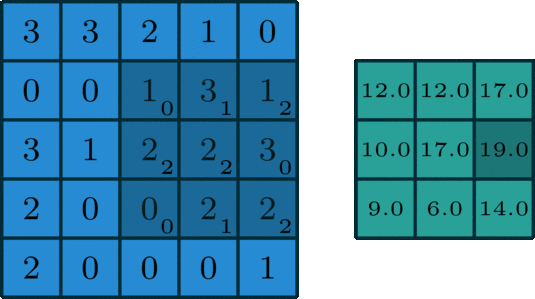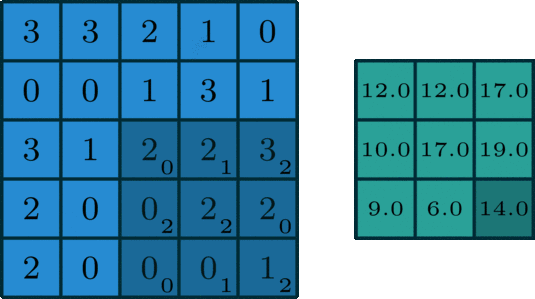
公式解釋，參考這裡，如下：

理解 FLOPs 的計算公式分兩步。括號內是第一步，計算出output feature map 的一個 pixel，然後再乘以 \(H\times W\times C_o\)，從而拓展到整個 output feature map。括號內的部分又可以分為兩步：\((2\times C_i\times K^2-1)=(C_i\times K^2) + (C_i\times K^2-1)\)。第一項是乘法運算次數，第二項是加法運算次數，因為 \(n\) 個數相加，要加 \(n-1\)次，所以不考慮 bias 的情況下，會有一個 -1，如果考慮 bias，剛好中和掉，括號內變為\((2\times C_i\times K^2)\)。

所以折積層的 \(FLOPs=(2\times C_{i}\times K^2-1)\times H\times W\times C_o\) (\(C_i\) 為輸入特徵圖通道數，\(K\) 為過濾器尺寸，\(H, W, C_o\)為輸出特徵圖的高，寬和通道數)。

全連線層的 FLOPs 計算

全連線層的 \(FLOPs = (2I − 1)O\)，\(I\) 是輸入層的維度，\(O\) 是輸出層的維度。

二，模型引數量分析

模型引數數量（params）：指模型含有多少引數，直接決定模型的大小，也影響推斷時對記憶體的佔用量，單位通常為 M，GPU 端通常引數用 float32 表示，所以模型大小是引數數量的 4 倍。這裡考慮的折積核長寬是相同的一般情況，都為 K。

模型引數量的分析是為了瞭解記憶體佔用情況，記憶體頻寬其實比 FLOPs 更重要。目前的計算機結構下，單次記憶體存取比單次運算慢得多的多。對每一層網路，端側裝置需要：

• 從主記憶體中讀取輸入向量 / feature map；
• 從主記憶體中讀取權重並計算點積；
• 將輸出向量或 feature map 寫回主記憶體。

MAes：memory accesse，記憶體存取次數。

折積層引數量

折積層權重引數量 = $ C_i\times K^2\times C_o + C_o$。

\(C_i\) 為輸入特徵圖通道數，\(K\) 為過濾器(折積核)尺寸，\(C_o\) 為輸出的特徵圖的 channel 數(也是 filter 的數量)，算式第二項是偏置項的引數量 。(一般不寫偏置項，偏置項對總引數量的數量級的影響可以忽略不記，這裡為了準確起見，把偏置項的引數量也考慮進來。）

假設輸入層矩陣維度是 96×96×3，第一層折積層使用尺寸為 5×5、深度為 16 的過濾器（折積核尺寸為 5×5、折積核數量為 16），那麼這層折積層的引數個數為 ５×5×3×16+16=1216個。

BN 層引數量

BN 層引數量 = \(2\times C_i\)。

其中 \(C_i\) 為輸入的 channel 數（BN層有兩個需要學習的引數，平移因子和縮放因子）

全連線層引數量

全連線層引數量 = \(T_i\times T_o + T_O\)。

\(T_i\) 為輸入向量的長度， \(T_o\) 為輸出向量的長度，公式的第二項為偏置項引數量。(目前全連線層已經逐漸被 Global Average Pooling 層取代了。) 注意，全連線層的權重引數量（記憶體佔用）遠遠大於折積層。

三，模型記憶體存取代價計算

MAC(memory access cost) 記憶體存取代價也叫記憶體使用量，指的是輸入單個樣本（一張影象），模型/折積層完成一次前向傳播所發生的記憶體交換總量，即模型的空間複雜度，單位是 Byte。

CNN 網路中每個網路層 MAC 的計算分為讀輸入 feature map 大小（DDR 讀）、權重大小（DDR 讀）和寫輸出 feature map 大小（DDR 寫）三部分。

折積層 MAC 計算

以折積層為例計算 MAC，可假設某個折積層輸入 feature map 大小是 (Cin, Hin, Win)，輸出 feature map 大小是 (Hout, Wout, Cout)，折積核是 (Cout, Cin, K, K)，理論 MAC（理論 MAC 一般小於 實際 MAC）計算公式如下：

# 端側推理IN8量化後模型，單位一般為 1 byte
input = Hin x Win x Cin  # 輸入 feature map 大小
output = Hout x Wout x Cout  # 輸出 feature map 大小
weights = K x K x Cin x Cout + bias   # bias 是折積層偏置
ddr_read = input +  weights
ddr_write = output
MAC = ddr_read + ddr_write

feature map 大小一般表示為 （N, C, H, W），MAC 指標一般用在端側模型推理中，端側模型推理模式一般都是單幀影象進行推理，即 N = 1(batch_size = 1)，不同於模型訓練時的 batch_size 大小一般大於 1。

四，一些概念

雙精度、單精度和半精度

CPU/GPU 的浮點計算能力得區分不同精度的浮點數，分為雙精度 FP64、單精度 FP32 和半精度 FP16。因為採用不同位數的浮點數的表達精度不一樣，所以造成的計算誤差也不一樣，對於需要處理的數位範圍大而且需要精確計算的科學計算來說，就要求採用雙精度浮點數，而對於常見的多媒體和圖形處理計算，32 位的單精度浮點計算已經足夠了，對於要求精度更低的機器學習等一些應用來說，半精度 16 位浮點數就可以甚至 8 位浮點數就已經夠用了。
對於浮點計算來說， CPU 可以同時支援不同精度的浮點運算，但在 GPU 裡針對單精度和雙精度就需要各自獨立的計算單元。

浮點計算能力

FLOPS：每秒浮點運算次數，每秒所執行的浮點運算次數，浮點運算包括了所有涉及小數的運算，比整數運算更費時間。下面幾個是表示浮點運算能力的單位。我們一般常用 TFLOPS(Tops) 作為衡量 NPU/GPU 效能/算力的指標，比如海思 3519AV100 晶片的算力為 1.7Tops 神經網路運算效能。

• MFLOPS（megaFLOPS）：等於每秒一佰萬（=10^6）次的浮點運算。
• GFLOPS（gigaFLOPS）：等於每秒拾億（=10^9）次的浮點運算。
• TFLOPS（teraFLOPS）：等於每秒萬億（=10^12）次的浮點運算。
• PFLOPS（petaFLOPS）：等於每秒千萬億（=10^15）次的浮點運算。
• EFLOPS（exaFLOPS）：等於每秒百億億（=10^18）次的浮點運算。

硬體利用率(Utilization)

在這種情況下，利用率（Utilization）是可以有效地用於實際工作負載的晶片的原始計算能力的百分比。深度學習和神經網路使用相對數量較少的計算原語（computational primitives），而這些數量很少的計算原語卻佔用了大部分計算時間。矩陣乘法（MM）和轉置是基本操作。MM 由乘法累加（MAC）操作組成。OPs/s（每秒完成操作的數量）指標通過每秒可以完成多少個 MAC（每次乘法和累加各被認為是 1 個 operation，因此 MAC 實際上是 2 個 OP）得到。所以我們可以將利用率定義為實際使用的運算能力和原始運算能力的比值：

五，參考資料

• PRUNING CONVOLUTIONAL NEURAL NETWORKS FOR RESOURCE EFFICIENT INFERENCE
• 神經網路引數量的計算：以UNet為例
• How fast is my model?
• MobileNetV1 & MobileNetV2 簡介
• 雙精度，單精度和半精度
• AI硬體的Computational Capacity詳解
• Roofline Model與深度學習模型的效能分析