【動手學深度學習】學習筆記
2022-11-26 21:01:29
線性神經網路
影象分類資料集
import torch
import torchvision
from matplotlib import pyplot as plt
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
# 在數位標籤索引以及文字名稱之間轉換
def get_fashion_mnist_labels(labels): #@save
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankel boot']
return [text_labels[int(i)] for i in labels] # 將索引與標籤一一對應
# 視覺化樣本
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5): #@save
figsize = (num_cols * scale, num_rows * scale)
_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
axes = axes.flatten() # 展開，方便索引
for i, (ax, img) in enumerate(zip(axes, imgs)):
if torch.is_tensor(img):
ax.imshow(img.numpy())
else:
ax.imshow(img)
ax.axes.get_xaxis().set_visible(False) # 隱藏座標軸
ax.axes.get_yaxis().set_visible(False)
if titles:
ax.set_title(titles[i])
return axes
"""
d2l.use_svg_display() # 使用svg顯示圖片，清晰度更高
# 讀取資料集
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="dataset/FashionMNIST",
train=True, transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="dataset/FashionMNIST",
train=False, transform=trans,
download=True)
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y))
plt.show()
"""
def get_dataloader_workers(): #@save
return 4 # 使用4個程序來讀取資料
# 定義函數用於獲取和讀取該資料集，返回訓練集和驗證集的迭代器
def load_data_fashion_mnist(batch_size, resize = None): #@save
trans = [transforms.ToTensor()]
if resize: # 如果需要更改尺寸
trans.insert(0,transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="dataset/FashionMNIST",
train=True, transform=trans,
download=False)
mnist_test = torchvision.datasets.FashionMNIST(root="dataset/FashionMNIST",
train=False, transform=trans,
download=False)
return (data.DataLoader(mnist_train,batch_size,shuffle=True,
num_workers=get_dataloader_workers()),
data.DataLoader(mnist_test, batch_size, shuffle=True,
num_workers=get_dataloader_workers()))
softmax迴歸的從零開始實現
import torch
from IPython import display
from d2l import torch as d2l
from matplotlib import pyplot as plt
btach_size = 256
# 呼叫之間的函數獲取兩個迭代器
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size=btach_size)
num_inputs = 784 # 將每個28和28的圖片展開成就是784，輸入大小
num_outputs = 10 # 輸入要預測十個類別
# 使用正態分佈來初始化權重，第三個引數是為了待會要計算梯度
W = torch.normal(0,0.01, size=(num_inputs,num_outputs),requires_grad=True)
b = torch.zeros(num_outputs,requires_grad=True)
def softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1,keepdim = True) # 求和仍然保持維度不變
return X_exp / partition
# 定義模型
def net(X):
return softmax(torch.matmul(X.reshape((-1,W.shape[0])),W)+b)
# 定義損失函數
def cross_entropy(y_hat,y):
return -torch.log(y_hat[range(len(y_hat)),y])
# 計算分類精度
def accuracy(y_hat,y): #@save
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis = 1) # 取出預測概率最大的下標
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
# 定義一個用來計算變數累加的類
class Accumulator: #@save
def __init__(self,n):
self.data = [0.0] * n
def add(self,*args): # 不限制輸入數目
self.data = [ a + float(b) for a,b in zip(self.data,args)]
def reset(self):
self.data = [0.0] * len(self.data) # 重置為0
def __getitem__(self, idx):
return self.data[idx]
# 評估在模型上的精度
def evaluate_accuracy(net,data_iter): #@save
if isinstance(net,torch.nn.Module): # 如果是當前已有的模組
net.eval() # 轉為評估模式，常在計算測試集精度時使用，該模式下不可以計算梯度
metric = Accumulator(2)
with torch.no_grad(): # 不計算精度
for X,y in data_iter:
metric.add(accuracy(net(X),y),y.numel()) # 第二個引數是統計tensor的個數
return metric[0] / metric[1]
# 訓練
def train_epoch_ch3(net,train_iter,loss,updater): #@save
# 將模型設定為訓練模式
if isinstance(net,torch.nn.Module):
net.train()
# 訓練損失總和，訓練精確度總和，樣本數
metric = Accumulator(3)
for X,y in train_iter:
y_hat = net(X) # 計算網路的輸出
l = loss(y_hat,y)
if isinstance(updater,torch.optim.Optimizer):
# 使用內建的優化器和損失函數
updater.zero_grad()
l.mean().backward()
updater.step()
else:
# 使用客製化的優化器和損失函數
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()),accuracy(y_hat,y),y.numel())
return metric[0]/metric[2],metric[1]/metric[2] # 返回訓練損失和訓練準確度
class Animator: #@save
def __init__(self,xlabel=None, ylabel = None, legend=None, xlim = None,ylim=None,xscale='linear',
yscale='linear',fmts=('-','m--','g-','r:'),nrows=1,ncols=1, figsize=(3.5,2.5)):
# 增量地繪製多條線
if legend is None:
legend=[]
d2l.use_svg_display()
self.fig,self.axes = d2l.plt.subplots(nrows,ncols,figsize=figsize) # 建立繪圖視窗
if nrows * ncols == 1:
self.axes = [self.axes,]
# 使用lambda函數捕獲引數
self.config_axes = lambda : d2l.set_axes(self.axes[0],xlabel,ylabel,xlim,ylim,xscale,yscale,legend)
self.X,self.Y,self.fmts = None,None,fmts
def add(self,x,y):
# 向圖表中新增多個資料點
if not hasattr(y,"__len__"): # 判斷範例物件y是否包含某個屬性或方法
y = [y]
n = len(y)
if not hasattr(x,"__len__"):
x = [x] * n
if not self.X:
self.X = [[] for _ in range(n)]
if not self.Y:
self.Y = [[] for _ in range(n)]
for i,(a,b) in enumerate(zip(x,y)):
if a is not None and b is not None:
self.X[i].append(a)
self.Y[i].append(b)
self.axes[0].cla()
for x,y,fmt in zip(self.X,self.Y,self.fmts):
self.axes[0].plot(x,y,fmt)
self.config_axes()
display.display(self.fig)
display.clear_output(wait=True)
# 實現一個訓練函數，它會在訓練資料集上訓練模型，並每輪會在測試集上計算誤差
def train_ch3(net,train_iter, test_iter, loss, num_epochs, updater): #@sace
animator = Animator(xlabel='epoch',xlim=[1,num_epochs],ylim = [0.3,0.9],
legend=['train loss','train acc','test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net,train_iter,loss,updater) # 每一輪的已寫過，返回誤差和精度
test_acc = evaluate_accuracy(net, test_iter) # 計算在測試集上的精度
animator.add(epoch+1, train_metrics+(test_acc,))
train_loss, train_acc = train_metrics # 遍歷了單次資料集當前的誤差和精度
assert train_loss < 0.5, train_loss # 如果不小於0.5就發生異常
assert train_acc <=1 and train_acc > 0.7, train_acc
assert test_acc <=1 and test_acc > 0.7, test_acc
lr = 0.1
def updater(batch_size):
return d2l.sgd([W,b],lr,batch_size)
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater) # 訓練模型
plt.show() # 在pycharm中最終使用這一句才會顯示出影象
# 預測測試集
def predict_ch3(net,test_iter, n=6): #@save
for X,y in test_iter:
break # 這裡只為了展示因此只取出第一份
trues = d2l.get_fashion_mnist_labels(y)
preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
titles = [true + '\n' + pred for true,pred in zip(trues,preds)] # 訓練取出真實和預測標籤
d2l.show_images(X[0:n].reshape((n,28,28)),1,n,titles = titles[0:n])
plt.show()
predict_ch3(net,test_iter)
softmax迴歸的簡潔實現
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 初始化模型引數
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
def init_weight(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01) # 給tensor初始化，一般是給網路中引數weight初始化，初始化引數值符合正態分佈
net.apply(init_weight) # 將初始化權重的操作應用於該父模組和各個子模組
loss = nn.CrossEntropyLoss(reduction='none') # 不對輸出執行均值或者求和的操作
optimer = torch.optim.SGD(net.parameters(),lr = 0.01)
num_epoch = 10
d2l.train_ch3(net,train_iter,test_iter, loss, num_epoch, optimer)
多層感知機
多層感知機的從零開始實現
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 初始化模型引數
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X @ W1 + b1) # @代表矩陣乘法的簡寫
return H @ W2 + b2
loss = nn.CrossEntropyLoss(reduction='none')
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
plt.show()
d2l.predict_ch3(net,test_iter)
plt.show()
多層感知機的簡潔實現
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
batch_size, lr, num_epochs = 256, 0.01, 10
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
optimer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter,test_iter, loss, num_epochs, optimer)
plt.show()
權重衰減
簡潔實現
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
optimer = torch.optim.SGD([ {"params":net[0].weight,'weight_decay':wd},
{"params":net[0].bias}],lr=lr)
上面設定「weight_decay」為wd就是設定其使用權重衰減。
Dropout
一個好的模型需要對輸入資料的擾動魯棒，也就是不能夠受噪聲的影響。那麼如果使用帶有噪聲的資料來學習的話，如果能夠使得其不學習到噪聲的那部分內容，那麼也相當於是正則化。因此丟棄法(Dropout)就是在層之間加入噪音。
那麼從定義方向出發，它就是無偏差的加入噪音，即對原本輸入\(\pmb{x}\)加入噪音得到\(\pmb{x}^{\prime}\)，希望其均值不變，即：
\[E[\pmb{x}^{\prime}]=\pmb{x}
\]
那麼丟棄法具體的做法是對每個元素執行如下擾動：
\[x^{\prime}_i=\begin{cases}
0\quad with~probablity~p\\
\frac{x_i}{1-p}\quad otherwise
\end{cases}
\]
那麼這樣可以保證期望不變：
\[E[x^{\prime}_i]=p\times 0 + (1-p)\times \frac{x_i}{1-p}=x_i
\]
那麼這個丟棄概率就是控制模型複雜度的超引數
具體是通常將丟棄法作用在多層感知機的隱藏層的輸出上，即：
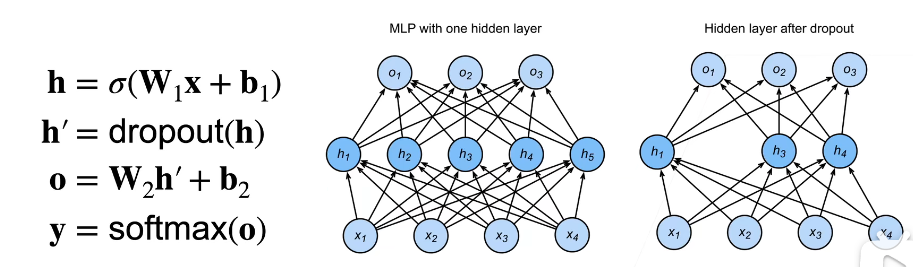
這是在訓練過程中使用，它將會影響模型引數的更新，而在測試的時候並不會進行dorpout操作，這樣能夠保證確定性的輸出。從實驗上來說，它和正則化能夠達到類似的效果。
那麼Dropout放在隱藏層的輸出，會將那些被置為0的神經元的權重在本次不進行更新，那麼就可以認為是每一次Dropout都是從所有的隱藏層神經元中挑選出一部分來進行更新。
具體的實現直接呼叫nn.Dropout()層即可。
數值穩定性
在計算梯度時：
因為向量對向量的求導是矩陣，因此這麼多次矩陣的運算可能會遇見梯度爆炸或者梯度消失的問題。
假設矩陣中的梯度大部分都是比1大一點的數，那麼經過這麼多次梯度計算就可能出現梯度過大而爆炸；那麼梯度如果稍微小於1也就會經過這麼多次迭代之後接近於0。
那麼梯度爆炸就會帶來如下的問題：
- 值超過了數值型別可以表示的範圍
- 對學習率更加敏感
- 當學習率比較大，乘上較大的梯度就更新程度比較大，難以穩定
- 當學習率太小，那麼可能導致在除開梯度爆炸的那些權重外的正常權重無法正常更新
而對於梯度消失，例如採用sigmoid函數：
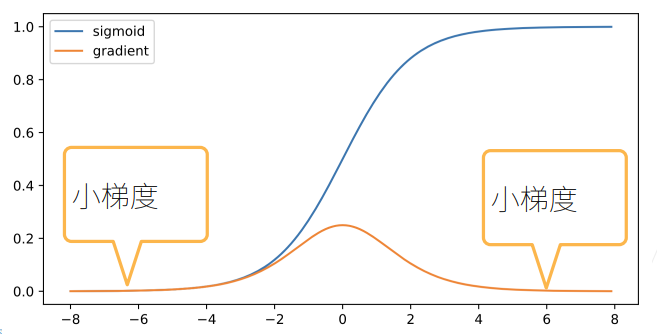
這麼小的梯度在多個疊加之後就可能會出現梯度消失的問題。它的主要問題是：
- 也是超過表示範圍，直接就使大部分梯度值為0，無法更新
- 訓練因為梯度值為0，無法正常更新
- 對於底部層尤為嚴重，因為梯度是從輸出層反向傳播計算得到的，越到底部層，疊加的層數越多，梯度越可能消失，那就使得只有頂部層能夠正常訓練更新
那麼如何使訓練更加穩定的首要目標，就是讓梯度值在合理的範圍內，例如在某些演演算法中它們將梯度的乘法轉換成加法，或者是對梯度進行歸一化、裁剪等。但還有一種重要的方法就是合理的進行權重初始化，以及選擇適合的啟用函數。
具體來說，結論就是在對權重進行初始化的時候，讓權重是從一個均值為0，方差為\(\gamma_t=\frac{2}{n_{t-1}+n_t}\)中取樣得到的。其中\(n_{t-1}、n_{t}\)代表該權重所連線的兩個層的神經元的數目。因此需要根據層的形狀來選擇權重所服從分佈的方差。
而啟用函數經過推導，可以認為tanh(x)和ReLU(x)這兩個啟用函數能夠具有較好的特性，而sigmoid(x)需要調整為\(4\times sigmoid(x)-2\)才能夠達到與前兩個相同的效果。
環境和分佈偏移
1、分佈偏移的型別
主要有以下幾種偏移型別：
- 協變數偏移：指的是資料的分佈\(p(x)\)發生了變化，例如在訓練的時候用到的訓練資料集分佈\(p_1(x)\)和測試的時候用到的測試集分佈\(p_2(x)\)不同，那麼這就很難使得模型在測試資料集上表現好。不過這種變化還有一個架設計就是雖然輸入的分佈可能隨時間發生變化，但是標籤函數(即條件分佈\(P(y\mid x)\))不會改變。例如在訓練的時候我們用真實的貓和狗來讓機器學會分類，但是在測試的時候我們用的是卡通的貓和狗，這就是訓練和測試兩部分的資料集不相同，但是它們的標籤函數是相同的，可以正確地對貓和狗進行標註。
- 標籤偏移：指的是和協變數偏移相反的問題，因為這裡假設標籤邊緣概率\(P(y)\)可以改變，但是類別條件分佈\(P(x\mid y)\)在不同的領域之間保持不變。這裡可以舉一個例子就是預測患者的疾病，症狀就是x，而所患的疾病就是標籤y，那麼疾病的相對流行率，或者說各種疾病之間的比例可能發生變化（即\(P(y)\)）可能發生變化，而對於某種特定疾病所對應的症狀(\(P(x\mid y))\)不會發生變化。
- 概念偏移：指的是標籤的定義出現了變化。舉個例子就是我們對於美貌的定義，可能會隨著時間的變化而發生變化，那麼這個「美貌」的標籤的概念就發生了變化。
2、分佈偏移糾正
首先需要了解什麼是經驗風險與實際風險：在訓練時我們通常是最小化損失函數（不考慮正則化項），即：
\[\min_{f} \frac{1}{Num}\sum_{i=1}^{Num} loss(f(x_i),y_i)
\]
這一項在訓練資料集上的損失稱為經驗風險。那麼經驗風險就是為了來近似真實風險的，也就是資料的真實分佈下的損失。然而在實際中我們無法獲得真實資料的分佈。因此一般認為最小化經驗風險可以近似於最小化真實風險。
協變數偏移糾正
對於目前已有的資料集(x,y)，我們要評估\(P(y\mid x)\)，但是當前的資料\(x_i\)是來源於某些源分佈\(q(x)\)(可以認為是訓練資料集的分佈)，而不是來源於目標分佈\(p(x)\)(可以認為是真實資料的分佈，或者認為是測試資料的分佈)。但存在協變數偏移的假設即\(p(y\mid x)=q(y\mid x)\)。因此：
\[\iint loss(f(x),y)p(x)dxdy~=~ \iint loss(f(x),y)q(y\mid x)q(x)\frac{p(x)}{q(x)}dxdy
\]
因此當前我們需要計算資料來自於目標分佈和來自於源分佈之間的比例，來重新衡量每個樣本的權重，即：
\[\beta_i=\frac{p(x_i)}{q(x_i)}
\]
那麼將該權重代入到每個資料樣本中，就可以使用加權經驗風險最小化來訓練模型：
\[\min_f \frac{1}{Num}\sum_{i=1}^{Num}\beta_i loss(f(x_i),y)
\]
因此接下來的問題就是估計\(\beta\)。具體的方法為：從兩個分佈中抽取樣本來進行分佈估計。即對於目標分佈\(p(x)\)我們就可以通過存取測試資料集來獲取；而對於源分佈\(q(x)\)則直接通過訓練資料集獲取。這裡需要考慮到存取測試資料集是否會導致資料洩露的問題，其實是不會的，因為我們只存取了特徵\(x \sim p(x)\)，並沒有存取其標籤y。在這種方法下，有一種非常有效的辦法來計算\(\beta\)：對數機率迴歸。
我們假設從兩個分佈中抽取相同資料的樣本，對於p抽取的樣本資料標籤為z=1，對於q抽取的樣本資料標籤為z=-1。因此該混合資料集的概率為：
\[P(z=1\mid x)=\frac{p(x)}{p(x)+q(x)}\\
\frac{P(z=1\mid x)}{P(z=-1\mid x)}=\frac{p(x)}{q(x)}
\]
因此如果我們使用對數機率迴歸的方法，即\(P(z=1\mid x)=\frac{1}{1+exp(-h(x))}\)（h是一個引數化函數，設定的），那麼就有：
\[\beta_i = \frac{P(z=1\mid x_i)}{P(z=-1 \mid x_i)}=exp(h(x_i))
\]
因此只要訓練得到\(h(x)\)即可。
但上述演演算法依賴一個重要的假設：需要目標分佈（測試集分佈）中的每個資料樣本在訓練時出現的概率非零，否則將會出現\(p(x_i)>0,q(x_i)=0\)的情況。
標籤偏移糾正
同樣，這裡假設標籤的分佈隨時間變化\(q(y)\neq p(y)\)，但類別條件分佈保持不變\(q(x\mid y)=p(x\mid y)\)。那麼：
\[\iint loss(f(x),y)p(x\mid y)p(y)dxdy=\iint loss(f(x),y)q(x\mid y)q(y)\frac{p(y)}{q(y)}dxdy
\]
因此重要性權重將對應於標籤似然比率：
\[\beta_i=\frac{p(y_i)}{q(y_i)}
\]
因為，為了顧及目標標籤的分佈，我們首先採用效能相當好的現成的分類器（通常基於訓練資料訓練得到），並使用驗證集計算混淆矩陣。那麼混淆矩陣是一個\(k\times k\)的矩陣（k為分類類別數目）。每個單元格的值\(c_{ij}\)是驗證集中真實標籤為j，而模型預測為i的樣本數量所佔的比例。
但是現在我們無法計算目標資料上的混淆矩陣，因為我們不知道真實分佈。那麼我們所能做的就是**將現有的模型在測試時的預測取平均數，得到平均模型輸出\(\mu (\hat{y})\in R^k\)，其中第i個元素為我們的模型預測測試集中第i個類別的總預測分數。
那麼具體來說，如果我們的分類器一開始就相當準確，並且目標資料只包含我們以前見過的類別（訓練集和測試集的擁有的類別是相同的），那麼如果標籤偏移假設成立，就可以通過一個簡單的線性系統來估計測試集的標籤分佈：
\[Cp(y)=\mu(\hat{y})
\]
因此若C可逆，則可得：
\[p(y)=C^{-1}\mu(\hat{y})
\]
概念偏移糾正
這個很難用什麼確切的方法來糾正。不過這種變化通常是很罕見的，或者是特別緩慢的。我們能夠做的一般是訓練時要適應網路的變化，使用新的資料來更新網路。
實戰kaggle比賽：預測房價
import numpy as np
import pandas as pd
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
import hashlib
import os
import tarfile
import zipfile
import requests
DATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'
def download(name, cache_dir=os.path.join("dataset", "data_kaggle")): # @save
assert name in DATA_HUB, f"{name} 不存在於 {DATA_HUB}"
url, shal_hash = DATA_HUB[name]
os.makedirs(cache_dir, exist_ok=True) # 按照第一個引數建立目錄，第二引數代表如果目錄已存在就不發出異常
fname = os.path.join(cache_dir, url.split('/')[-1])
if os.path.exists(fname): # 如果已存在這個資料集
shal = hashlib.sha1()
with open(fname, 'rb') as f:
while True:
data = f.read(1048576) # 這裡進行資料集的讀取，一次能夠讀取的最大行數為1048576
if not data: # 如果讀取到某一次不成功
break
shal.update(data)
if shal.hexdigest() == shal_hash:
return fname # 命中快取
print(f'正在從{url}下載{fname}...')
r = requests.get(url, stream=True, verify=True)
# 向連結傳送請求，第二個引數是不立即下載，當資料迭代器存取的時候再去下載那部分，不然全部載入會爆記憶體，第三個引數為不驗證證書
with open(fname, 'wb') as f:
f.write(r.content)
return fname
# 下載並解壓一個zip或tar檔案
def download_extract(name, folder=None): # @save
fname = download(name)
base_dir = os.path.dirname(fname) # 獲取檔案的路徑，fname是一個相對路徑，那麼就返回從當前檔案到目標檔案的路徑
data_dir, ext = os.path.splitext(fname) # 將這個路徑最後的檔名分割，返回路徑+檔名，和一個檔案的擴充套件名
if ext == '.zip': # 如果為zip檔案
fp = zipfile.ZipFile(fname, 'r')
elif ext in ('.tar', '.gz'):
fp = tarfile.open(fname, 'r')
else:
assert False, "只有zip/tar檔案才可以被解壓縮"
fp.extractall(base_dir) # 解壓壓縮包內的所有檔案到base_dir
return os.path.join(base_dir, folder) if folder else data_dir
def download_all(): # @save
for name in DATA_HUB:
download(name)
# 下載並快取房屋資料集
DATA_HUB['kaggle_house_train'] = ( # @save
DATA_URL + 'kaggle_house_pred_train.csv',
'585e9cc93e70b39160e7921475f9bcd7d31219ce'
)
DATA_HUB['kaggle_house_test'] = ( # @save
DATA_URL + 'kaggle_house_pred_test.csv',
'fa19780a7b011d9b009e8bff8e99922a8ee2eb90'
)
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
# print(train_data.shape)
# print(test_data.shape)
# print(train_data.iloc[0:4,[0,1,2,3,-3,-2,-1]])
# 將序號列去掉,訓練資料也不包含最後一列的價格列，然後將訓練資料集和測試資料集縱向連線在一起
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
# 將數值型的資料統一減去均值和方差
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index # 在panda中object型別代表字串
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()) # 應用匿名函數
)
# 在標準化資料後，所有均值消失，因此我們可以設定缺失值為0
all_features[numeric_features] = all_features[numeric_features].fillna(0)
# 對離散值進行處理
all_features = pd.get_dummies(all_features, dummy_na=True) # 第二個引數代表是否對nan型別進行編碼
# print(all_features.shape)
n_train = train_data.shape[0] # 訓練資料集的個數
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float32) # 取出訓練資料
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float32) # 取出測試資料
train_labels = torch.tensor(train_data.SalePrice.values.reshape(-1, 1), dtype=torch.float32) # 取出訓練資料的價格列
loss = nn.MSELoss()
in_features = train_features.shape[1] # 特徵的個數
# 網路架構
def get_net():
net = nn.Sequential(nn.Linear(in_features, 1))
return net
# 取對數約束輸出的數量級
def log_rmes(net, features, labels):
clipped_preds = torch.clamp(net(features), 1, float('inf'))
# 第一個為要約束的引數，第二個為最小值，第三個為最大值，小於最小值就為1
rmse = torch.sqrt(loss(torch.log(clipped_preds), torch.log(labels)))
return rmse.item()
# 訓練的函數
def train(net, train_features, train_labels, test_features, test_labels, num_epochs, learning_rate,
weight_decay, batch_size):
train_ls, test_ls = [], []
train_iter = d2l.load_array((train_features, train_labels), batch_size) # 獲取資料迭代器
optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate, weight_decay=weight_decay)
# 這是另外一個優化器，它對lr的數值不太敏感，第三個引數代表是否使用正則化
for epoch in range(num_epochs):
for X, y in train_iter:
optimizer.zero_grad() # 梯度先清零
l = loss(net(X), y) # 計算損失
l.backward() # 反向傳播計算梯度
optimizer.step() # 更新引數
train_ls.append(log_rmes(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmes(net, test_features, test_labels))
return train_ls, test_ls
# K折交叉驗證
def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size) # 建立一個切片物件
X_part, y_part = X[idx, :], y[idx] # 將切片物件應用於索引
if j == i: # 取出第i份作為驗證集
X_valid, y_valid = X_part, y_part
elif X_train is None: # 如果當前訓練集沒有資料就初始化
X_train, y_train = X_part, y_part
else:
X_train = torch.cat([X_train, X_part], 0) # 如果是訓練集那麼就進行合併
y_train = torch.cat([y_train, y_part], 0)
return X_train, y_train, X_valid, y_valid
# k次的k折交叉驗證
def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay, batch_size):
train_l_sum, valid_l_sum = 0, 0
for i in range(k):
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net()
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size)
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i == 0:
d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls], xlabel="epoch",
ylabel='ylabel', xlim=[1, num_epochs], legend=["train", 'valid'], yscale='log')
print(f"折{i + 1},訓練log rmse{float(train_ls[-1]):f},"
f"驗證log rmse{float(valid_ls[-1]):f}")
return train_l_sum / k, valid_l_sum / k
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l,valid_l = k_fold(k,train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
print(f"{k}折驗證：平均訓練log rmse:{float(train_l):f}",
f"平均驗證log rmse:{float(valid_l):f}")
plt.show()
下面為我自己偵錯的結果：
def get_net():
net = nn.Sequential(nn.Linear(in_features, 256),
nn.ReLU(),
nn.Linear(256,1))
return net
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
5折驗證：平均訓練log rmse:0.045112 平均驗證log rmse:0.157140
我總感覺256直接到1不太好，因此調整了模型的結構：
def get_net():
net = nn.Sequential(nn.Linear(in_features, 128),
nn.ReLU(),
nn.Linear(128,1))
return net
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 0.03, 1, 64
5折驗證：平均訓練log rmse:0.109637 平均驗證log rmse:0.136201
更復雜的模型總感覺沒辦法再降低誤差了。
深度學習計算
層與塊
自定義Sequential模組：
class MySequential(nn.Module):
def __init__(self, *args):
super().__init__()
for idx, module in enumerate(args):
self._modules[str(idx)] = module
# _modules是一個用來存放模組的地方，它的好處是方便存取，類似於一個字典
def forward(self,X):
for block in self._modules.values():
X = block(X)
return X
如果想要某些引數不更新，那麼可以設定requires_grad=False，即
self.rand_weight = torch.rand((20,20),requires_grad=False)
小結：
一個塊可以由許多層組成，一個塊也可以由許多塊組成
塊內可以包含我們自定義的程式碼
塊負責大量的內部處理，包括引數初始化和反向傳播
層與塊的順序連線由Sequential塊處理
引數管理
引數存取有很多種方式，如下：
net = nn.Sequential(nn.Linear(4,8),nn.ReLU(), nn.Linear(8,1))
net[2].state_dict() # 存取索引為2的模型（第二個Linear）的狀態字典，其中就包含權重和偏置的引數
net[2].bias
net[2].bias.data # 取出值
引數初始化：
def init_normal(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, mean=0, std=0.01) # 呼叫正態分佈初始化，當然也有很多其他分佈方法
nn.init.zeros_(m.bias) # 初始化為0
net.apply(m) # 為nn內部的linear全部初始化引數
引數繫結：
shared = nn.Linear(8,8)
net = nn.Sequential(nn.Linear(4,8),nn.ReLU(), shared, nn.ReLU(), shard, nn.ReLU())
這樣兩個shared層之間的引數就一直保持相同，共用引數。需要是同一個範例化物件才會共用引數的。
自定義層
自定義層和自定義網路很類似：
class MyLinear(nn.Module): # 要整合這個負類
def __init__(self, in_units, units):
super().__init__() # 同樣初始化
self.weight = nn.Parameter(torch.randn(in_units, units)) # 定義引數時要用這個函數
self.bias = nn.Parameter(torch.randn(units,))
def forward(self,X):
linear = torch.matmul(X, self.weight.data)+self.bias.data
return F.relu(linear)
那麼就跟其他層一樣可以正常使用了。
讀寫檔案
對於資料的儲存可採用如下方式：
torch.save(x,"檔名")
y = torch.load("檔名")
也可以多個x,y進行儲存。
而對於模型的儲存：
class MLP(nn.Module):
---------這裡省略了定義
net = MLP()
torch.save(net.state_dict(), "檔名") # 將引數儲存起來
clone = MLP() # 必須先範例化一個物件才可以來接收儲存的引數
clone.load_state_dict(torch.load("檔名"))
GPU
import torch
from torch import nn
print(torch.cuda.device_count()) # 查詢可用的GPU數量
def try_gpu(i=0): # @save
if torch.cuda.device_count() >= i + 1:
return torch.device(f'cuda:{i}') # 返回目標的那個gpu
return torch.device('cpu') # 如果不滿足則返回cpu
def try_all_gpus(): # @save
devices = [torch.device(f'cuda:{i}') for i in range(torch.cuda.device_count())]
return devices if devices else [torch.device('cpu')]
print(try_gpu())
print(try_gpu(10))
print(try_all_gpus())
1
cuda:0
cpu
[device(type='cuda', index=0)]
那麼接下來就是將模型、輸入、loss這三部分挪到GPU上，那麼就可以在GPU上進行計算。
X = torch.ones(2, 3, device=try_gpu())
# 如果有多個gpu，也需要在同一個gpu上運算：Z = X.cuda(1)
net = nn.Sequential(nn.Linear(3,1))
net = net.to(device=try_gpu())
print(net[0].weight.data.device)
需要注意的是，一般來說資料的處理是先在cpu上做，處理完成後再移動到GPU上和網路進行計算。
折積神經網路
從全連線層到折積
小結：
- 影象的平移不變性使得我們以相同的方式處理區域性影象，而不在乎它所在的位置
- 區域性性意味著計算相應的隱藏表示只需要一小部分的區域性影象畫素
- 在影象處理中，折積層通常比全連線層需要更少的引數，但依舊獲得高效用的效能
- 折積神經網路CNN是一類特殊的神經網路，它可以包含多個折積層
- 多個輸入和輸出通道使模型造每個空間位置可以獲得影象的多方面特徵
影象折積
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): # @save
h, w = K.shape # 折積核的大小
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
X = torch.ones((6,8))
X[:,2:6] = 0
K = torch.tensor([[1.0,-1.0]])
Y = corr2d(X,K)
print(Y)
填充和步幅度
噹噹輸入影象的形狀為\(n_h \times n_w\)，折積形狀為\(k_h \times k_w\)時，那麼輸出形狀為\((n_h-k_h+1)\times (n_w -k_w+1)\)。
那麼若填充\(p_h\)行和\(p_w\)列（分別進行上下左右平均分類），那麼最終輸出的形狀為：
\[(n_h -k_h + p_h + 1)\times(n_w-k_w+p_w+1)
\]
若調整垂直步幅為\(s_h\)，水平步幅為\(s_w\)時，輸出形狀為：
\[\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor (n_w-k_w+p_w+s_w)/s_w \rfloor
\]
import torch
from torch import nn
def comp_conv2d(conv2d,x):
x = x.reshape((1,1) + X.shape) # 將維度弄成4個，前兩個為填充和步幅
y = conv2d(x)
return y.reshape(y.shape[2:])
conv2d = nn.Conv2d(1,1,kernel_size=(3,5),padding=(0,1),stride=(3,4))
X = torch.rand(size=(8,8))
print(comp_conv2d(conv2d,X).shape)
小結：
- 填充可以增加輸出的高度和寬度，這常用來使得輸出與輸入具有相同的高和寬
- 步幅可以減小輸出的高和寬，例如輸出的高和寬僅為輸入的高和寬的\(\frac{1}{n}\)
- 填充和步幅可用於有效地調整資料的維度
多輸入多輸出通道
對於多輸入通道來說，一般都有相同通道數的折積核來跟其進行匹配，然後計算的過程就是對每個通道輸入的二維張量和對應通道的折積核的二維張量進行運算，每個通道得到一個計算結果，然後就將各個計算結果相加作為輸出的單通道的那個位置的數值，如下圖：
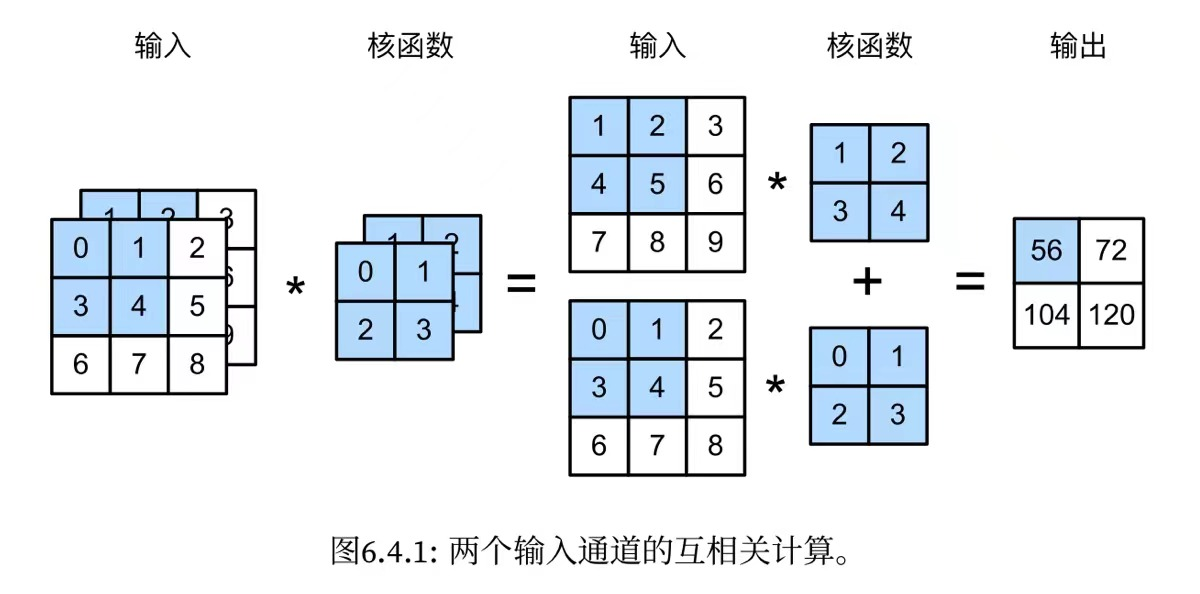
對於多輸出通道來說，可以將每個通道看作是對不同特徵的響應，假設\(c_i、c_o\)分別為輸入和輸出通道的數目，那麼為了得到這多個通道的輸出，我們需要為每個輸出通道建立一個形狀為\(c_i\times k_h \times k_w\)大小的折積核張量，因此總的折積核的形狀為\(c_o\times c_i \times k_h \times k_w\)。
而還有一種特殊的折積層，為\(1\times 1\)折積層。因為高寬只有1，因此它無法造高度和寬度的維度上，識別相鄰元素間相互作用的能力，它唯一的計算髮生在通道上。如下圖：
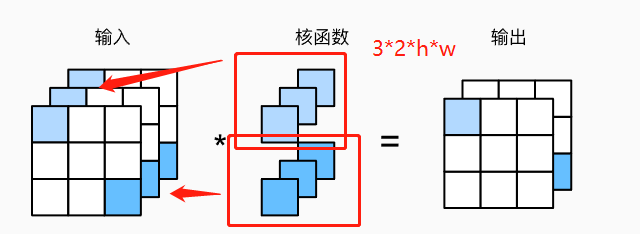
這種折積層會導致輸入和輸出具有相同的高度和寬度，但是通道數發生了變化，輸出中的每個元素都是從輸入影象中同一位置的元素的線性組合，這就說明可以將這個折積層起的作用看成是一個全連線層，輸入的每個通道就是一個輸入結點，然後折積核的每一個通道就是對應的權重。
因此\(1\times 1\)折積層通常用於調整網路層的通 道數量和控制模型的複雜度
池化層（匯聚層）
池化層可以用來處理折積對於畫素位置尤其敏感的問題，例如下面：
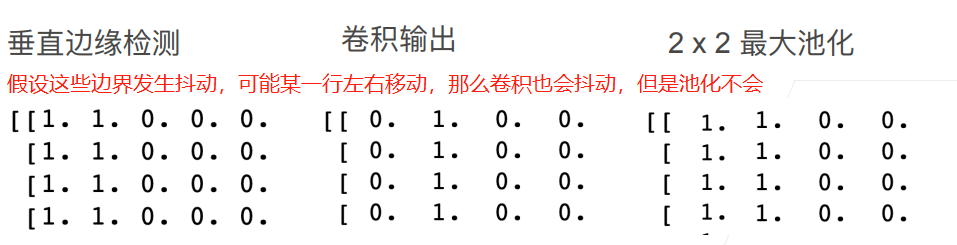
那麼池化有最大池化以及平均池化
具體實現為：
pool2d = nn.MaxPool2d((2,3),padding=(1,1),stride=(2,3))
如果應對多通道的場景，會保持輸入和輸出通道相等。
小結：
- 對於給定輸入元素，最大池化層會輸出該視窗內的最大值，平均池化層會輸出該視窗內的平均值
- 池化層的主要優點之一是減輕折積層對位置的過度敏感
- 可以指定池化層的填充和步幅
- 使用最大池化層以及大於1的步幅，可以減小空間的維度
- 池化層的輸出通道數和輸入通道數相同
折積神經網路(LeNet)
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
class Reshape(torch.nn.Module):
def forward(self, x):
return x.view(-1, 1, 28, 28)
net = nn.Sequential(
Reshape(),
nn.Conv2d(1, 6, kernel_size=5, padding=2),
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5),
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
# 載入資料集
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)
# 修改評估函數，使用GPU來計算
def evaluate_accuracy_gpu(net, data_iter, device=None): # @save
if isinstance(net, torch.nn.Module):
net.eval() # 轉為評估模式
if not device: # 如果不是為None
device = next(iter(net.parameters())).device
metric = d2l.Accumulator(2)
for X,y in data_iter:
if isinstance(X, list):
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
metric.add(d2l.accuracy(net(X),y), y.numel())
return metric[0] / metric[1]
# 對訓練函數做改動，使其能夠在GPU上跑
def train_ch6(net, train_iter, test_iter, num_eopchs, lr, device): #@ save
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print("training on:",device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', xlim=[1,num_eopchs],
legend=["train loss",'train acc', 'test,acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_eopchs):
metric = d2l.Accumulator(3)
net.train() # 開啟訓練模式
for i,(X,y) in enumerate(train_iter):
timer.start() # 開始計時
optimizer.zero_grad() # 清空梯度
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat,y), X.shape[0])
timer.stop() # 停止計時
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i+1) % (num_batches // 5) == 0 or i==num_batches-1:
animator.add(epoch + (i+ 1) / num_batches,
(train_l, train_acc ,None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch+1, (None, None, test_acc))
print(f'loss{ train_l:.3f},train acc{train_acc:.3f},'
f'test acc{test_acc:.3f}')
print(f'{metric[2] * num_eopchs / timer.sum():1f} examples / sec'
f'on{str(device)}')
lr, num_epoch = 0.5,20
train_ch6(net, train_iter, test_iter, num_epoch, lr ,d2l.try_gpu())
plt.show()
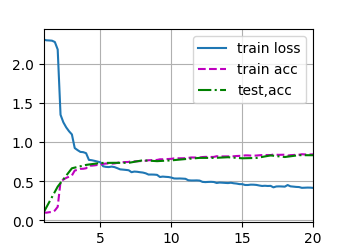
loss0.417,train acc0.847,test acc0.836
36144.960085 examples / seconcuda:0
小結：
- 折積神經網路是一類使用折積層的網路
- 在折積神經網路中，組合使用折積層、非線性啟用函數和池化層
- 為了構造高效能的CNN，我們通常對摺積層進行排序，逐漸降低其表示的空間解析度，同時增加通道數
- 在傳統的折積神經網路中，折積塊編碼得到的表徵在輸出之前需要由一個或多個全連線層進行處理
- LeNet是最早釋出的折積神經網路之一
深度折積神經網路(AlexNet)
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(96, 256, kernel_size=5, padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(256, 384, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
nn.Linear(6400, 4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 10)
)
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
# 讀取資料然後將其高和寬都拉成224
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
跑了好久：
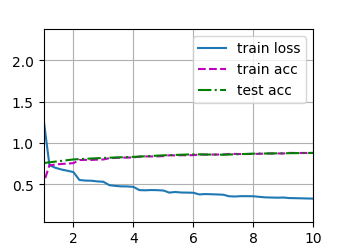
loss 0.328, train acc 0.881, test acc 0.881
666.9 examples/sec on cuda:0
使用塊的網路(VGG)
VGG就是沿用了AlexNet的思想，將多個折積層和一個池化層組成一個塊，然後可以指定每個塊內折積層的數目，以及塊的數目，經過多個塊對影象資訊的提取後再經過全連線層。
VGG塊中包含以下內容：
- 多個帶填充以保持解析度不變的折積層
- 每個折積層後都帶有非線性啟用函數
- 最後一個池化層
具體程式碼如下：
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
def vgg_block(num_convs, in_channels, out_channels):
# 該函數用來建立單個的VGG塊
layers = []
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2, stride=2))
return nn.Sequential(*layers)
def vgg(conv_arch):
conv_blks = []
in_channels = 1
# 構建折積層
for (num_convs, out_channels) in conv_arch:
conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
in_channels = out_channels
return nn.Sequential(
*conv_blks,
nn.Flatten(),
nn.Linear(out_channels * 7 * 7, 4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 10)
)
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))
# 第一個為塊內折積層個數，第二個為輸出通道數
ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
# 除以ratio減少通道數目
net = vgg(small_conv_arch)
lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net,train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
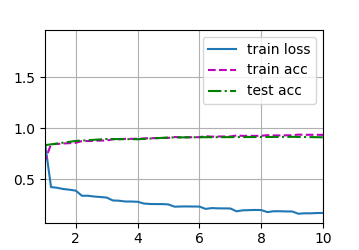
loss 0.170, train acc 0.936, test acc 0.912
378.0 examples/sec on cuda:0
小結：
- VGG-11使用可複用的折積塊來構造網路，不同的VGG模型可通過每個塊中折積層數量和輸出通道數量的差異來定義
- 塊的使用導致網路定義得非常簡潔，使用塊可以有效地設計複雜的網路
- 在研究中發現深層且窄的折積（多層\(3\times 3\)）比淺層且寬（例如少層\(5\times 5\)）的效果更好
網路中的網路（NiN）
之前的網路都有一個共同的特點在於最後都會通過全連線層來對特徵的表示進行處理，這就導致引數數量很大。那麼NiN就是希望能夠很其他的模組來替換掉全連線層，那麼就用到了\(1 \times 1\)的折積層，因此1個NiN塊就是一個正常的折積層和兩個\(1 \times 1\)的折積層，那麼經過多個NiN塊後，將通道數拓展到希望輸出的類別數，然後用一個具有輸出類別數目的通道數的全域性平均池化層來進行處理，也就是對每個通道進行全部平均得到單個標量，那麼有\(out\_channels\)個通道就有相應個數值，再經過softmax就可以作為輸出了。
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
# 在第一個折積層就將其轉換為對應的通道數和大小
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1),
nn.ReLU() # 兩個1*1的折積層都不改變大小和通道
)
net = nn.Sequential(
nin_block(1, 96, kernel_size=11, strides=4, padding=0),
nn.MaxPool2d(3, stride=2), # 使得高寬減半
nin_block(96, 256, kernel_size=5, strides=1, padding=2),
nn.MaxPool2d(3,stride=2),
nin_block(256, 384, kernel_size=3, strides=1, padding=1),
nn.MaxPool2d(3,stride=2),
nn.Dropout(p=0.5),
# 標籤類別數為10，因此最後一個輸出通道數設為10
nin_block(384, 10, kernel_size=3, strides=1, padding=1),
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten() # 將四維度的轉成兩個維度（批次大小，輸出通道數）
)
lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
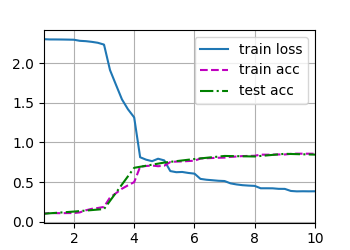
loss 0.383, train acc 0.857, test acc 0.847
513.3 examples/sec on cuda:0
小結：
- NiN使用由一個折積層和多個\(1\times 1\)折積層組成的塊，該塊可以在折積神經網路中使用，以允許更多的畫素非線性
- NiN去除了容易造成過擬合的全連線層，將它們替換成全域性平均池化層，該池化層通道數量為所需的輸出數目
- 移除全連線層可以減少過擬合，同時顯著減少引數量
含並行連線的網路(GoogLeNet)
前面提到的各種網路，其中的問題在於各個折積層的引數可能都是不一樣的，而DNN的解釋性如此之差，我們很難解釋清楚哪一個超引數的折積層才是我們需要的，才是最好的。因此在GoogLeNet網路中，其引入了Inception塊，這種塊引入了平行計算的思想，將常見的多種不同超引數的折積層都放入，希望能夠通過多種提取特徵的方式來得到最理想的特徵提取效果，如下圖：
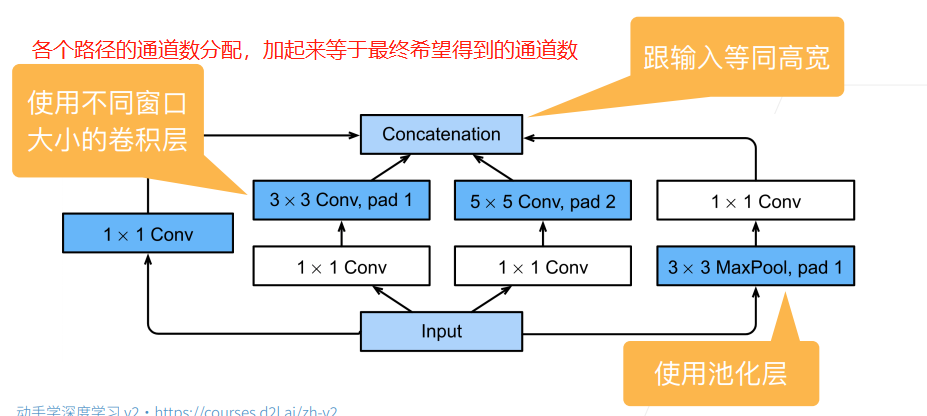
其具體的結構為：
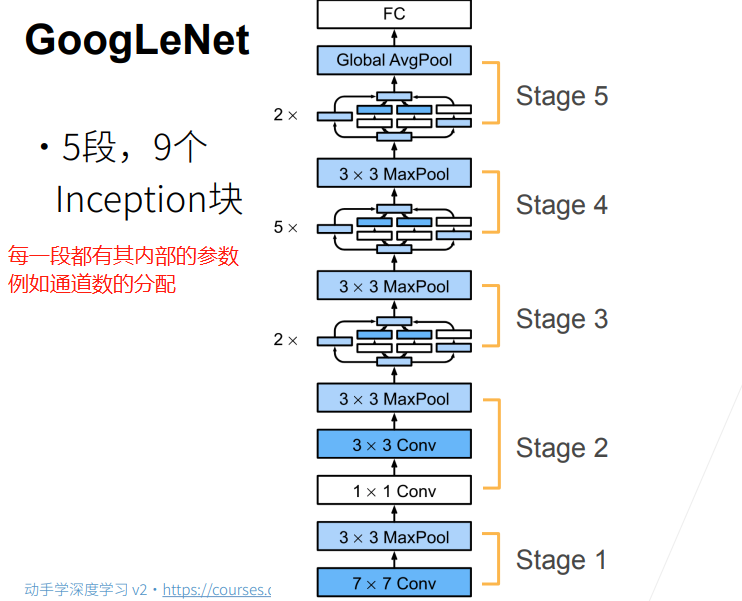
import torch
from matplotlib import pyplot as plt
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Inception(nn.Module):
def __init__(self, in_channels, c1,c2,c3, c4, **kwargs):
super(Inception, self).__init__(**kwargs)
# 線路1，單1*1折積層
self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
# 線路2,1*1折積層後接3*3折積層
self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
self.p2_2 = nn.Conv2d(c2[0],c2[1], kernel_size=3, padding=1)
# 線路3,1*1折積層後接上5*5折積層
self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
# 線路4,3*3最大池化層後接上1*1折積層
self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1,padding=1)
self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)
def forward(self,x):
p1 = F.relu(self.p1_1(x))
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
p4 = F.relu(self.p4_2(self.p4_1(x)))
# 再在通道維度上疊加在一起
return torch.cat((p1,p2,p3,p4),dim=1)
b1 = nn.Sequential(
nn.Conv2d(1,64, kernel_size=7, stride=2, padding=3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
b2 = nn.Sequential(
nn.Conv2d(64, 64, kernel_size=1),
nn.ReLU(),
nn.Conv2d(64, 192, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
b3 = nn.Sequential(
Inception(192,64,(96,128),(16,32),32),
Inception(256,128,(128,192),(32,96),64),
nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)
b4 = nn.Sequential(
Inception(480, 192, (96,208),(16,48), 64),
Inception(512, 160, (112,224),(24,64), 64),
Inception(512,128,(128,256),(24,64),64),
Inception(512,112, (144,288),(32,64), 64),
Inception(528, 256, (160,320),(32,128),128),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
b5 = nn.Sequential(
Inception(832,256, (160,320),(32,128),128),
Inception(832, 384, (192,384), (48,128),128),
nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten()
)
net = nn.Sequential(
b1,b2,b3,b4,b5,nn.Linear(1024,10)
)
lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
"""
x = torch.rand(size=(1,1,96,96))
for layer in net:
x = layer(x)
print(layer.__class__.__name__, 'output shape \t', x.shape)
"""
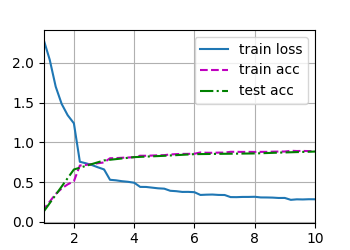
loss 0.284, train acc 0.891, test acc 0.884
731.9 examples/sec on cuda:0
小結：
- Inception塊相當於一個有4條路徑的子網路，它通過不同視窗形狀的折積層和最大池化層來並行抽取資訊，並使用\(1\times 1\)折積層減少每畫素級別上的通道維數從而降低模型複雜度
- GoogLeNet將多個設計精細的Inception塊與其他層（折積層、全連線層）串聯起來，其中Inception塊的通道數分配之比是在ImageNet資料集上通過大量的實驗得到的
- GoogLeNet和它的後繼者們一度是ImageNet上最有效的模型之一：它以較低的計算複雜度提供了類似的測試精度
批次歸一化
在訓練過程中，一般正常情況下，後面的層的梯度會比較大，而前面層的梯度會因為經過多層的傳播一直相乘而變得比較小，而此時學習率如果固定的話，那麼前面的層就會更新得比較慢，後面層會更新得比較快，那麼當後面層更新即將完成時，會因為前面的層發生了變動，那麼後面層就需要重新更新。
那麼批次規範化的思想是：在每一個折積層或線型層後應用，將其輸出規範到某一個分佈之中（不同的層所歸到的分佈是不一樣的，是各自學習的），那麼限制到一個想要的分佈後便可以使得收斂更快。
假設當前批次B得到的樣本為\(\pmb{x}=(x_1,x_2,...,x_n)\)，那麼：
\[\hat{\mu}_B=\frac{1}{\vert B\vert}\sum_{i\in B}x_i\\
\hat{\sigma}^2_B=\frac{1}{\vert B \vert}\sum_{i\in B}(x_i -\hat{\mu}_B)^2+\epsilon~~(\epsilon防止方差為0)\\
BN(x_i)=\gamma \frac{x_i - \hat{\mu}_B}{\hat{\sigma}_B}+\beta
\]
可以認為\(\gamma、\beta\)分別為要規範到的分佈的方差和均值，是兩個待學習的引數。
研究指出，其作用可能就是通過在每個小批次中加入噪音來控制模型的複雜度，因為批次是隨機取得的，因此批次的均值和方差也就不同，相當於對該次批次加入了隨機偏移\(\hat{\mu}_B\)和隨機縮放\(\hat{\sigma}_B\)。需要注意的是它不需要與Dropout一起使用。
它可以作用的全連線層和折積層的輸出上，啟用函數之前，也可以作用到全連線層和折積層的輸入上：
- 對於全連線層來說，其作用在特徵維
- 對於折積層，作用在通道維
而當我們在訓練中採用和批次歸一化，我們就需要記下來每個用到批次歸一化的地方，其整個樣本資料集的均值和方差是多少，這樣才能夠在進行預測的時候也對預測樣本進行規範。
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
if not torch.is_grad_enabled(): # 說明當前在預測
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps) # 防止方差為0
# 這兩個引數就是整個資料集的均值和方差
else:
assert len(X.shape) in (2,4) # 維度數目為2，是全連線層，為4是折積層
if len(X.shape) == 2:
mean = X.mean(dim = 0)
var = ((X - mean) ** 2 ).mean(dim = 0)
else:
mean = X.mean(dim=(0,2,3),keepdim=True)
# 每一個通道是一個不同的特徵，其提取了影象不同的特徵，因此對通道維計算均值方差
var = ((X - mean) ** 2).mean(dim=(0,2,3), keepdim = True)
# 當前在訓練模式
X_hat = (X - mean) / torch.sqrt(var + eps)
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta
return Y, moving_mean.data, moving_var.data
class BatchNorm(nn.Module):
def __init__(self,num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
Y,self.moving_mean, self.moving_var = batch_norm(X,self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5),
BatchNorm(6, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16,kernel_size=5),
BatchNorm(16, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 4 * 4, 120),
BatchNorm(120, num_dims=2),
nn.Sigmoid(),
nn.Linear(120, 84),
BatchNorm(84, num_dims=2),
nn.Sigmoid(),
nn.Linear(84, 10))
lr, num_epochs, batch_size = 1.0, 10 ,256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net,train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
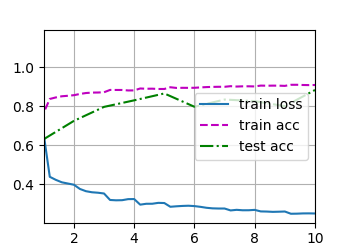
loss 0.251, train acc 0.908, test acc 0.883
17375.8 examples/sec on cuda:0
而nn中也有簡單的實現方法：
net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5),
nn.BatchNorm2d(6),
nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16,kernel_size=5),
nn.BatchNorm2d(16),
nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 4 * 4, 120),
nn.BatchNorm2d(120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.BatchNorm2d(84),
nn.Sigmoid(),
nn.Linear(84, 10))
小結：
- 在模型訓練的過程中，批次歸一化利用小批次的均值和標準差，不斷調整神經網路的中間輸出，使整個神經網路各層的中間輸出更加穩定
- 批次歸一化在全連線層和折積層的使用略有不同，需要注意作用的維度
- 批次歸一化和Dropout一樣，在訓練模式和預測模式下計算不同
- 批次歸一化有許多有益的副作用，主要是正則化
殘差網路(ResNet)
我們需要討論一個問題是：是否加入更多的層就能夠使得精度進一步提高？
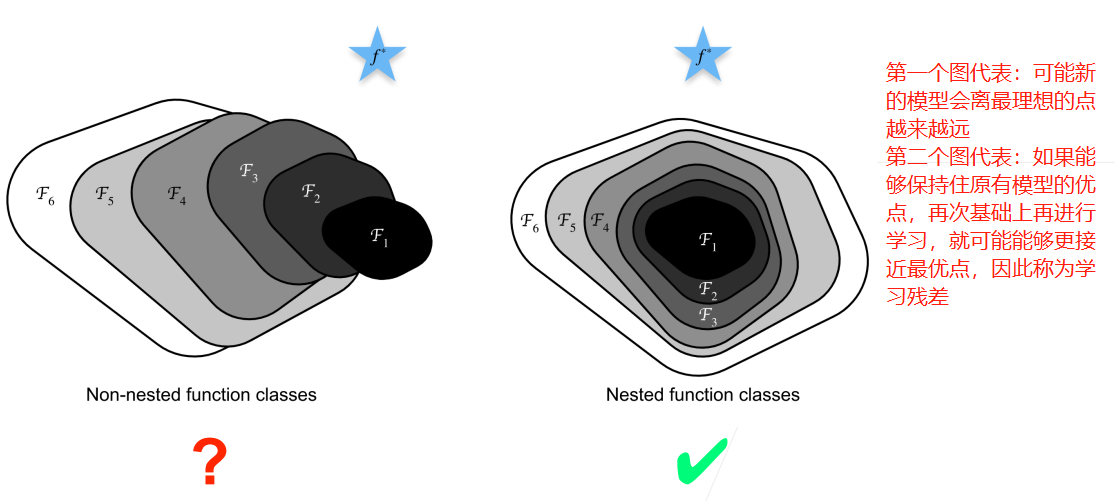
因此ResNet就是這種思想，最具體的表現是：
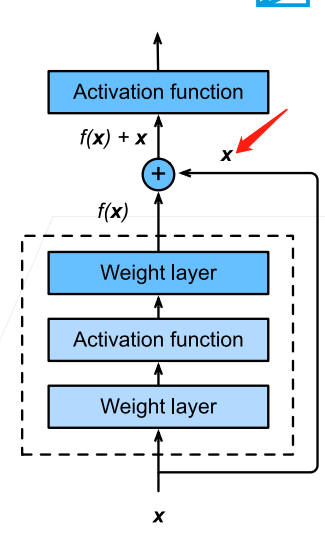
那麼將該塊的輸入連線到輸出，就需要輸入和輸出的維度是相同的，可以直接相加，因此如果塊內部對維度進行了改變，那麼就需要對輸入也進行維度的變化才能夠相加：
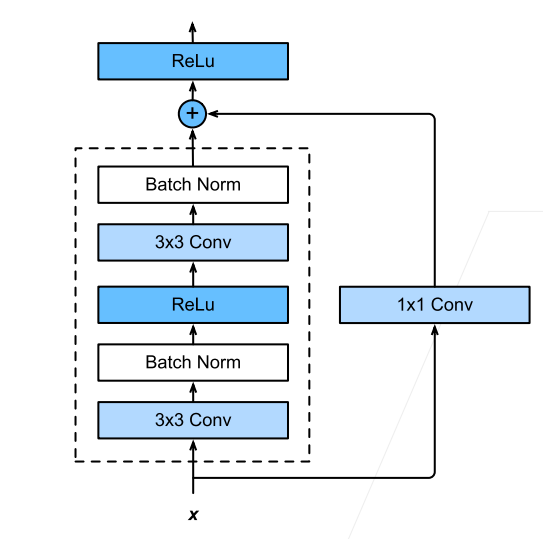
那麼一般來說，是先對輸入進行多個高寬減半的ResNet塊，後面再接多個高寬不變的ResNet塊，可以使得後面提取特徵的時候減少計算量：
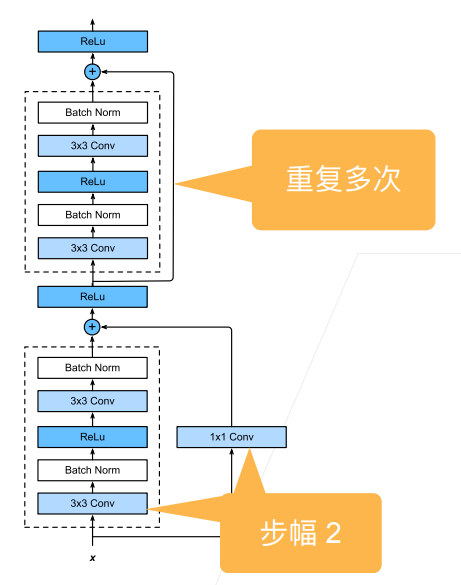
那麼整體的架構就是：
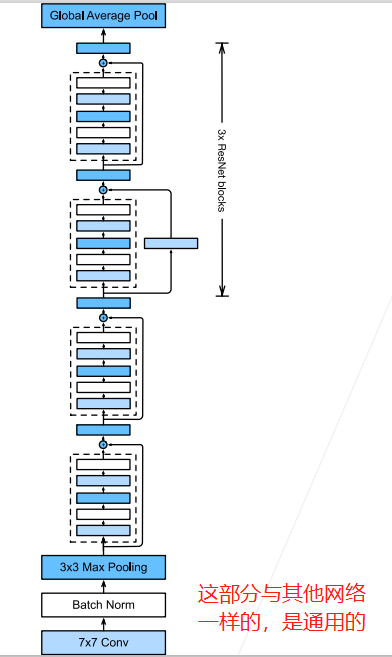
因此，程式碼為：
import torch
from matplotlib import pyplot as plt
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual(nn.Module): #@save
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)
# 第一個模組基本上在折積神經網路中都是一樣的
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(input_channels, num_channels, num_residuals,first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64,64,2,first_block=True))
b3 = nn.Sequential(*resnet_block(64,128,2))
b4 = nn.Sequential(*resnet_block(128,256,2))
b5 = nn.Sequential(*resnet_block(256,512,2))
# *號代表把resnet_block返回的列表展開，可以理解為把元素都拿出來，不是單個列表了
net = nn.Sequential(
b1,b2,b3,b4,b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(512,10)
)
"""
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t', X.shape)
"""
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
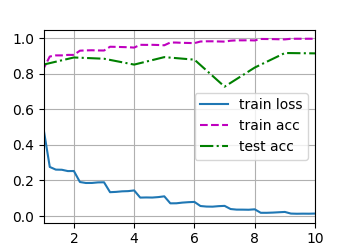
loss 0.014, train acc 0.996, test acc 0.914
883.9 examples/sec on cuda:0
李沐老師後面又補充了一節關於ResNet的梯度計算的內容，具體如下：
\[假設y=f(x)，則更新為~~w=w-\lambda \frac{\partial y}{\partial w}\\
那麼假設後面增加一個模組為y^{\prime}=g(y)=g(f(x))，則此時輸出關於引數的導數為~\frac{\partial y^{\prime}}{\partial w}=\frac{\partial g(y)}{\partial y}\frac{\partial y}{\partial w}\\
那麼如果g是一個學習能力比較強的層（例如全連線層），那麼就會更接近於真實輸出，此時\frac{\partial g(y)}{\partial y}較小\\
從而導致\frac{\partial y^{\prime}}{\partial w}較小，那麼f(x)層的更新就很慢，主要問題就是乘法\\
中間一個比較小就會出現梯度消失的問題\\
而ResNet它採用了殘差的方式，即y^{\prime}=f(x)+g(f(x))，那麼\frac{\partial y^{\prime}}{\partial w}=\frac{\partial y}{\partial w}+\frac{\partial g(y)}{\partial y}\frac{\partial y}{\partial w}\\
就算第二部分較小，仍然有第一部分來提供較大的梯度。\\因此可以解決梯度消失的問題，在靠近資料部分的也能夠進行更新
\]
影象分類競賽
本次我先是採用了李沐老師上課講過的ResNet11去跑，結果達到了0.8多一點，具體的程式碼請見下：
# 首先匯入包
import torch
import torch.nn as nn
import pandas as pd
import numpy as np
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms
from PIL import Image
import os
from d2l import torch as d2l
import matplotlib.pyplot as plt
from LeavesDataset import LeavesDataset # 資料載入器
先是要對標籤類的資料進行處理，將其從字串轉換為對應的類別數位，同時在這兩者之間建立關係方便後續：
label_dataorgin = pd.read_csv("dataset/classify-leaves/train.csv") # 讀取csv檔案
leaves_labels = sorted(list(set(label_dataorgin['label']))) # 取出標籤列然後set去重再列表排序
num_class = len(leaves_labels) # 總共的類別數目
class_to_num = dict(zip(leaves_labels, range(num_class))) # 建立字典，類別名稱對應數位
num_to_class = {i:j for j,i in class_to_num.items()} # 數位對應類別名稱
接下來就是寫我們資料載入器，因為我發現一個問題就是如果把資料載入器和整體的程式碼寫在同樣的檔案中會報錯，會在之後呼叫d2l的訓練函數時說找不到這個資料載入器的定義，那麼我們需要在另外的檔案寫資料載入器的定義然後參照，我在另外的LeavesDataset.py檔案中為其定義：
class LeavesDataset(Dataset):
def __init__(self, csv_path, file_path, mode = 'train', valid_ratio = 0.2,
resize_height = 256, resize_width=256):
self.resize_height = resize_height # 拉伸的高度
self.resize_width = resize_width # 寬度
self.file_path = file_path # 檔案路徑
self.mode = mode # 模式
self.data_csv = pd.read_csv(csv_path, header=None) # 讀取csv檔案去除表頭
self.dataLength = len(self.data_csv.index) - 1 # 資料長度
self.trainLength = int(self.dataLength * (1 - valid_ratio)) # 訓練集的長度
if mode == 'train':
# 訓練模式
self.train_images = np.asarray(self.data_csv.iloc[1:self.trainLength, 0]) # 第0列為影象的名稱
self.train_labels = np.asarray(self.data_csv.iloc[1:self.trainLength, 1]) # 第1列為影象的標籤
self.image_arr = self.train_images
self.label_arr = self.image_arr
elif mode == 'valid':
self.valid_images = np.asarray(self.data_csv.iloc[self.trainLength:, 0])
self.valid_labels = np.asarray(self.data_csv.iloc[self.trainLength:, 1])
self.image_arr = self.valid_images
self.label_arr = self.valid_labels
elif mode == 'test':
self.test_images = np.asarray(self.data_csv.iloc[1:,0]) # 測試集沒有標籤列
self.image_arr = self.test_images
self.realLen_now = len(self.image_arr)
print("{}模式下已完成資料載入，得到{}個資料".format(mode, self.realLen_now))
def __getitem__(self, index):
image_name = self.image_arr[index] # 得到檔名
img = Image.open(os.path.join(self.file_path, image_name)) # 拼接後得到當前存取圖片的完整路徑
transform = transforms.Compose([
transforms.Resize((224,224)), # 更改為224*224
transforms.ToTensor()
])
img = transform(img)
if self.mode == 'test':
return img
else:
label = self.label_arr[index]
number_label = class_to_num[label]
return img, number_label
def __len__(self):
return self.realLen_now
那麼接下來就是載入各個資料集了：
train_path = "dataset/classify-leaves/train.csv" # 根據你的實際情況修改
test_path = "dataset/classify-leaves/test.csv"
img_path = "dataset/classify-leaves/"
train_dataset = LeavesDataset(train_path, img_path, mode = 'train')
valid_dataset = LeavesDataset(train_path, img_path, mode = 'valid')
test_dataset = LeavesDataset(test_path, img_path, mode = 'test')
batch_size = 64 # 這裡如果視訊記憶體不夠可以調小
train_loader = DataLoader(dataset=train_dataset,batch_size=batch_size, shuffle=False,num_workers=5) # 不隨機打亂，程序數為5
valid_loader = DataLoader(dataset=valid_dataset,batch_size=batch_size, shuffle=False,num_workers=5)
test_loader = DataLoader(dataset=test_dataset,batch_size=batch_size, shuffle=False,num_workers=5)
得到資料後接下來就是定義模型了，我先是採用了ResNet11：
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(input_channels, num_channels, num_residuals,first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(d2l.Residual(input_channels, num_channels,use_1x1conv=True, strides=2))
else:
blk.append(d2l.Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64,64,2,first_block=True))
b3 = nn.Sequential(*resnet_block(64,128,2))
b4 = nn.Sequential(*resnet_block(128,256,2))
b5 = nn.Sequential(*resnet_block(256,512,2))
net = nn.Sequential(
b1,b2,b3,b4,b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(512,176)
)
然後因為我希望如果模型能夠達到要求的精度我就將其儲存下來，因此修改了訓練函數：
def train_ch6_save(net, train_iter, test_iter, num_epochs, lr, device, best_acc): #@save
"""Train a model with a GPU (defined in Chapter 6).
Defined in :numref:`sec_lenet`"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# Sum of training loss, sum of training accuracy, no. of examples
metric = d2l.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')
if test_acc > best_acc:
print("模型精度較高，值得儲存！")
torch.save(net.state_dict(), "Now_Best_Module.pth")
else:
print("模型精度不夠，不值得儲存")
lr, num_epochs,best_acc = 0.05, 25, 0.8 # epoch太小訓練不完全
train_ch6_save(net, train_loader, valid_loader, num_epochs, lr, device=d2l.try_gpu(), best_acc=best_acc)
plt.show()
得到結果為：
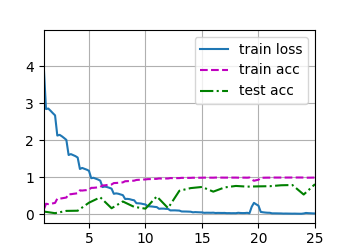
那麼我接下來希望加大ResNet的深度來提高模型複雜度，用了網上的ResNet50模型發現太大了，讀完模型之後再讀資料，就算把batch_size設定小也視訊記憶體爆了，因此只能修改模型小一點：
b2 = nn.Sequential(*resnet_block(64,64,2,first_block=True))
b3 = nn.Sequential(*resnet_block(64,256,2))
b4 = nn.Sequential(*resnet_block(256,512,2))
b5 = nn.Sequential(*resnet_block(512,2048,3))
net = nn.Sequential(
b1,b2,b3,b4,b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(2048,176)
)
跑了五個小時結果過擬合了...
loss 0.014, train acc 0.996, test acc 0.764
31.6 examples/sec on cuda:0
最終偵錯了好幾個模型花費了一整天的時間，還是沒有最開始的ResNet11的效果好，最終決定就用這個了。
因此完整的程式碼為：
# 首先匯入包
import torch
import torch.nn as nn
import pandas as pd
import numpy as np
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms
from PIL import Image
import os
from d2l import torch as d2l
import matplotlib.pyplot as plt
from tqdm import tqdm
from LeavesDataset import LeavesDataset
def resnet_block(input_channels, num_channels, num_residuals, first_block=False): # 這是ResNet定義用到的函數
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(d2l.Residual(input_channels, num_channels, use_1x1conv=True, strides=2))
else:
blk.append(d2l.Residual(num_channels, num_channels))
return blk
def train_ch6_save(net, train_iter, test_iter, num_epochs, lr, device, best_acc): # @save
"""Train a model with a GPU (defined in Chapter 6).
這是因為我需要訓練完儲存因此將老師的訓練函數進行了修改，就放在這裡了
Defined in :numref:`sec_lenet`"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# Sum of training loss, sum of training accuracy, no. of examples
metric = d2l.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
timer.start()
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')
if test_acc > best_acc:
print("模型精度較高，值得儲存！")
torch.save(net.state_dict(), "Now_Best_Module.pth") # 對模型進行儲存
else:
print("模型精度不夠，不值得儲存")
if __name__ == "__main__": # 一定要將執行的程式碼放在這裡！否則會報錯，我目前還不知道原因
label_dataorgin = pd.read_csv("dataset/classify-leaves/train.csv") # 讀取訓練的csv檔案
leaves_labels = sorted(list(set(label_dataorgin['label']))) # 取出標籤列然後去重再排序
num_class = len(leaves_labels) # 類別的個數
class_to_num = dict(zip(leaves_labels, range(num_class))) # 轉換為字典
num_to_class = {i: j for j, i in class_to_num.items()}
train_path = "dataset/classify-leaves/train.csv"
test_path = "dataset/classify-leaves/test.csv"
img_path = "dataset/classify-leaves/"
submission_path = "dataset/classify-leaves/submission.csv" # 最終要提交的檔案的路徑
train_dataset = LeavesDataset(train_path, img_path, mode='train')
valid_dataset = LeavesDataset(train_path, img_path, mode='valid')
test_dataset = LeavesDataset(test_path, img_path, mode='test')
#print("資料載入完成")
batch_size = 64
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=False, num_workers=5)
valid_loader = DataLoader(dataset=valid_dataset, batch_size=batch_size, shuffle=False, num_workers=5)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False, num_workers=5)
#print("資料已變換為loader")
# 定義模型
# 第一個模組基本上在折積神經網路中都是一樣的
b1 = nn.Sequential(nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(
b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(),
nn.Linear(512, 176)
)
lr, num_epochs, best_acc = 0.02, 15, 0.85
device = d2l.try_gpu()
train_ch6_save(net, train_loader, valid_loader, num_epochs, lr, device=device, best_acc=best_acc)
plt.show()
# 開始做預測
net.load_state_dict(torch.load("Now_Best_Module.pth")) # 載入模型
# print("模型載入完成")
net.to(device)
net.eval() # 開啟預測模式
predictions = [] # 用來存放結果類別對應的數位
for i, data in enumerate(test_loader):
imgs = data.to(device)
with torch.no_grad():
logits = net(imgs) # 計算結果是一個176長的向量
predictions.extend(logits.argmax(dim=-1).cpu().numpy().tolist())
# 取出最大的作為結果，並且放回cpu中，再轉換成列表方便插入到predictions中
preds = []
for i in predictions:
preds.append(num_to_class[i]) # 轉換為字串
test_csv = pd.read_csv(test_path)
test_csv['label'] = pd.Series(preds) # 將結果作為一個新的列新增
submission = pd.concat([test_csv['image'], test_csv['label']], axis=1) # 拼接
submission.to_csv(submission_path, index=False) # 寫入檔案
提交的分數為：
自己還是非常開心的！第一次完完整整地完成了一個專案，真正地學到了很多東西！只有自己動手從零開始才真正明白自己哪部分欠缺，因此才能夠有進步！
請繼續努力吧！
稠密連線網路(DenseNet)
與ResNet相比，DenseNet具有更加稠密連線的特點。
之前的ResNet通常是每個層，會與它前面的某一層相連線，按照元素相加的方式結合，如下圖：
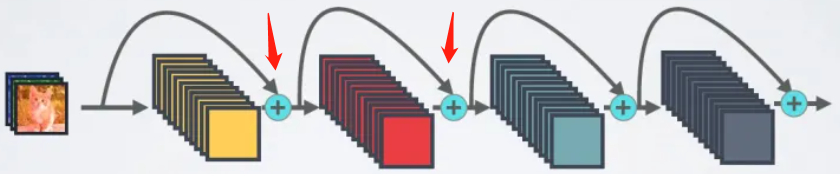
而DenseNet不同，它是每個層都會與前面所有層相連線，而且連線的方式是在通道維度上拼接在一起，這樣對於一個\(L\)層的網路，DenseNet共包含有\(\frac{L(L+1)}{2}\)個連線，因此是一種密集連線型。
如果要數位化來表示這種關係，假設傳統的網路在第\(l\)層的輸出為：
\[x_l=H_l(x_{l-1})
\]
那麼ResNet的輸出為：
\[x_l=H_l(x_{l-1})+x_{l-1}
\]
而DenseNet的輸出為：
\[x_l=H_l([x_0,x_1,...,x_{l-1}])
\]
稠密網路主要由兩部分構成：稠密塊和過渡層。前者定義如何連線輸入和輸出，後者則控制通道數量，使其不會太複雜。
具體程式碼如下：
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
def conv_block(input_channels, num_channels): # 改良版的折積
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1)
)
class DenseBlock(nn.Module):
# 一個稠密塊由多個折積塊組成，每個折積塊使用相同數量的輸出通道
def __init__(self, num_convs, input_channels, num_channels):
super(DenseBlock,self).__init__()
layer = []
for i in range(num_convs):
layer.append(conv_block( num_channels * i + input_channels, num_channels))
# 因此每次都會加上前面輸入的通道數目
self.net = nn.Sequential(*layer)
def forward(self,X):
for blk in self.net:
Y = blk(X)
X = torch.cat((X,Y), dim = 1) # 進行通道維度的連線
return X
def transition_block(input_channels, num_channels):
# 這一層使用1*1的折積層來減小通道數，使用步幅為2的平均池化層來減半高寬，防止模型太複雜
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2)
)
if __name__ == "__main__":
"""
blk = DenseBlock(2,3,10)
X = torch.rand(4,3,8,8)
Y = blk(X)
print(Y.shape)
blk2 = transition_block(23,10)
print(blk2(Y).shape)
"""
b1 = nn.Sequential(
nn.Conv2d(1,64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
num_channels, growth_rate = 64,32 # 第二個引數是指每一個折積層輸出為多少通道
num_convs_in_dense_blocks = [4,4,4,4] # 這個是每一個稠密塊中有多少個折積層
# 每個稠密塊4個折積層，每個折積層輸出為32，因此每個稠密塊增加通道數為4*32=128
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
blks.append(DenseBlock(num_convs, num_channels, growth_rate))
num_channels += num_convs * growth_rate # 每個稠密塊執行完都要修改輸出通道數
if i != len(num_convs_in_dense_blocks) - 1:
# 在稠密塊之間新增轉換層，使其通道數量減半
blks.append(transition_block(num_channels, num_channels//2))
num_channels = num_channels // 2
net = nn.Sequential(
b1,
*blks,
nn.BatchNorm2d(num_channels),
nn.ReLU(),
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(num_channels,10)
)
lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()
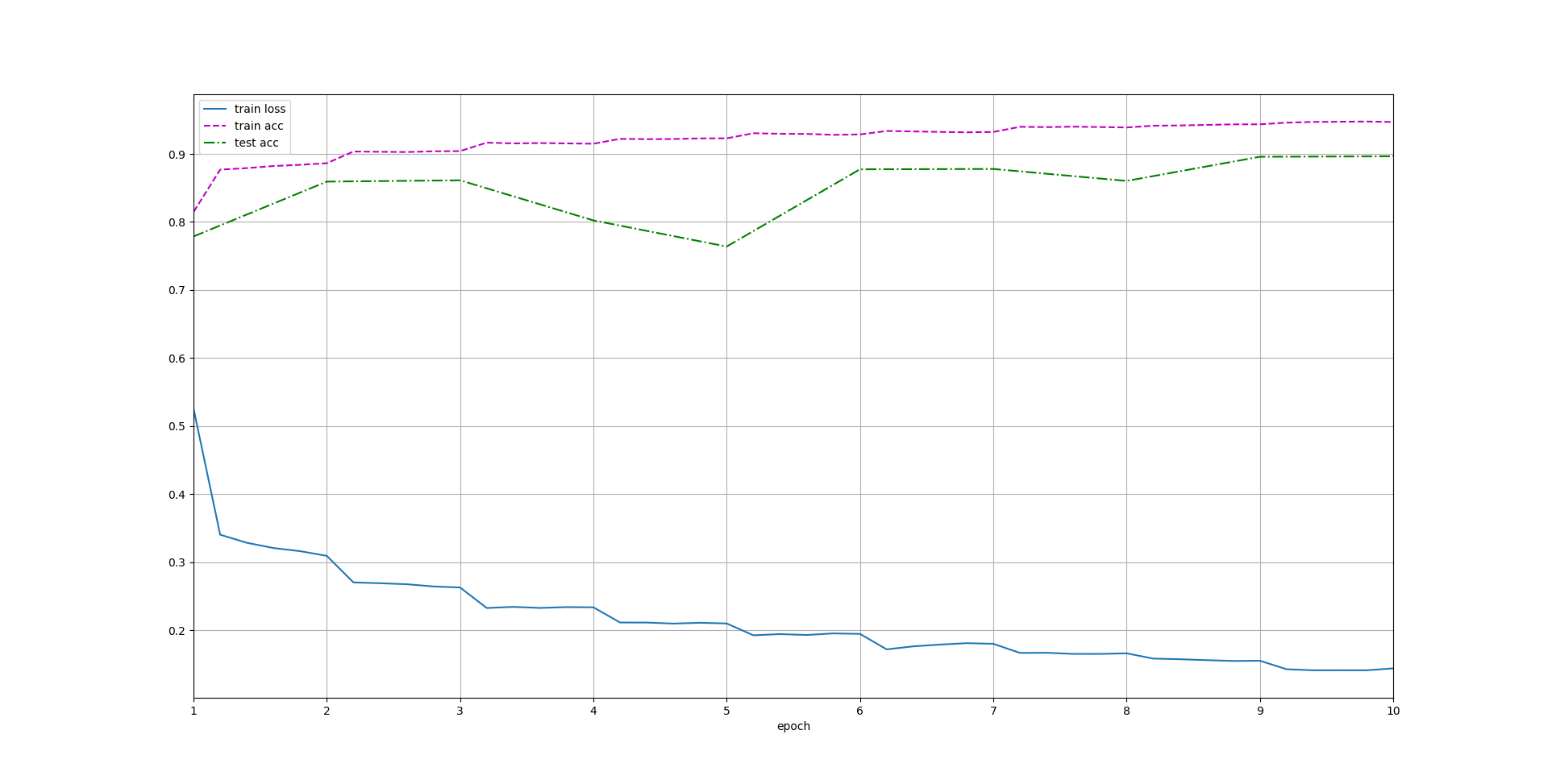
loss 0.144, train acc 0.947, test acc 0.896
1030.5 examples/sec on cuda:0
小結：
- 在跨層連線上，不同於ResNet中將輸入與輸出按元素相加，DenseNet在通道維上連線輸入和輸出
- DenseNet的主要構建模組是稠密塊與過渡層
- 在構建DenseNet時，我們需要通過新增過渡層來控制網路的維數，從而再次減少通道的數量
計算機視覺
影象增廣
影象增廣實際上就是對資料進行增強，使得資料集具有更多的多樣性，常見的增強方法有：
- 切割：從圖片中切割一塊，然後變形到固定形狀
- 顏色：改變色調、飽和度、明亮度等等
具體程式碼如下：
import torch
import torchvision
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
d2l.set_figsize()
img = d2l.Image.open("cat.jpg")
d2l.plt.imshow(img)
plt.show()
定義函數方便應用各種變幻效果：
# 該函數可以將各種變幻直接用aug引數傳入
def apply(img, aug, num_row=2, num_cols=4, scale=1.5):
Y = [aug(img) for _ in range(num_row * num_cols)]
d2l.show_images(Y, num_row, num_cols, scale=scale)
翻轉：
左右翻轉：
apply(img, torchvision.transforms.RandomHorizontalFlip()) # 隨機左右翻轉
plt.show()
上下翻轉：
apply(img, torchvision.transforms.RandomVerticalFlip()) # 隨機上下翻轉
plt.show()
裁剪：
shape_aug = torchvision.transforms.RandomResizedCrop(
(200,200), scale=(0.1,1), ratio=(0.5,2)
) # 隨機裁剪面積為10%到100%，裁剪後縮放到200，寬高比從0.5到2之間取值
apply(img,shape_aug)
plt.show()
改變亮度：
apply(img, torchvision.transforms.ColorJitter(
brightness=0.5, contrast=0, saturation=0, hue=0
)) # 隨機改變亮度為原始的50% 到150%之間
plt.show()
改變色調：
apply(img, torchvision.transforms.ColorJitter(
brightness=0, contrast=0, saturation=0, hue=0.5))
plt.show()
隨機改變亮度、對比度、飽和度、色調：
color_aug = torchvision.transforms.ColorJitter(
brightness=0.5, contrast=0.5, saturation=0.5, hue=0.5)
apply(img, color_aug)
plt.show()
結合多種影象增廣辦法：
augs = torchvision.transforms.Compose([
torchvision.transforms.RandomHorizontalFlip(), color_aug, shape_aug])
apply(img, augs)
plt.show()
利用影象增廣來訓練模型：
batch_size, devices, net = 256, d2l.try_gpu(), d2l.resnet18(10,3)
def load_cifar10(is_train, augs, batch_size):
dataset = torchvision.datasets.CIFAR10(root="dataset", train=is_train,
transform=augs, download=True)
dataloader = DataLoader(dataset, batch_size=batch_size,
shuffle=is_train, num_workers=d2l.get_dataloader_workers())
return dataloader
def train_with_data_aug(train_augs, test_augs, net, lr=0.001):
train_iter = load_cifar10(True, train_augs, batch_size=batch_size)
test_iter = load_cifar10(False, test_augs, batch_size=batch_size)
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.Adam(net.parameters(),lr=lr)
d2l.train_ch6(net, train_iter, test_iter, 10, lr, devices)
train_augs = torchvision.transforms.Compose([
torchvision.transforms.RandomHorizontalFlip(), # 隨機左右翻轉
torchvision.transforms.ToTensor()])
test_augs = torchvision.transforms.Compose([ # 測試集不做增廣，只轉為tensor
torchvision.transforms.ToTensor()])
def init_weights(m):
if type(m) in [nn.Linear, nn.Conv2d]:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
train_with_data_aug(train_augs, test_augs, net)
plt.show()
因為我的電腦只有一個GPU，因此就直接用原來的訓練函數了。
不知道為什麼跑出來的結果就很爛...
loss 0.181, train acc 0.943, test acc 0.655
650.8 examples/sec on cuda:0
小結：
- 影象增廣基於現有的訓練資料生成隨機影象，來提高模型的泛化能力
- 為了在預測過程中得到確切的結果，我們通常只對訓練樣本進行影象增廣，而對於測試樣本不使用帶有隨機操作的影象增廣
- 深度學習框架提供了許多不同的影象增廣辦法，這些方法可以被同時應用
微調
一個神經網路一般可以分成兩個部分，分別是特徵抽取和線性分類器部分，前者將原始畫素變成容易線型分割的特徵，後者用來進行分類。
那麼如果我們擁有一個在龐巨量資料集上已經訓練好的模型，那麼可以認為特徵提取部分學習到了比較通用的提取方法，對我們想要應用的新資料集可能是有用的，而線性部分因為標籤已經發生了變化因此無法重複利用，因此一般是將已經訓練好的模型的特徵提取部分直接copy到新模型中，然後隨機初始化最後的線性分類層，這樣就叫做微調，
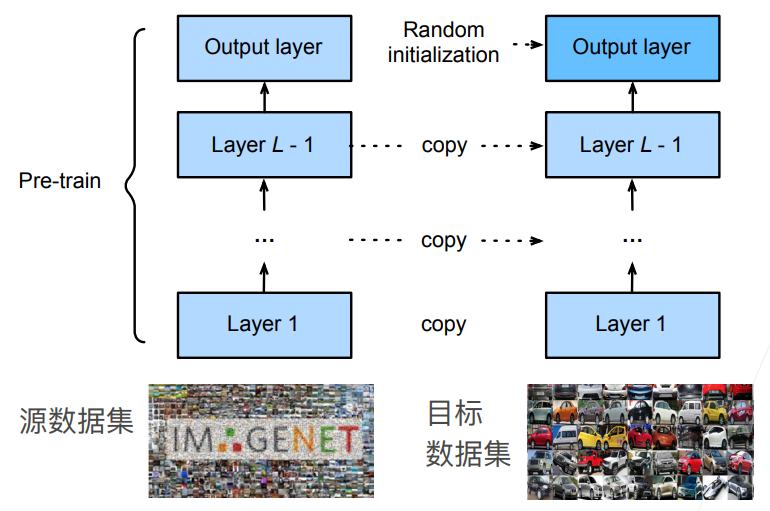
而在訓練的時候通常會採用更強的正則化，即在那些重用的特徵提取層的引數一般使用很小的學習率進行修改，並且學習迭代次數也比較少，而最後的線性分類層是使用較大的學習率來修改，甚至可以固定底部的某些特徵提取層不變（因為底部的才是更加通用的）來減少模型複雜度。
具體程式碼如下：
import os
import torch
import torchvision
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
#@save
from torch.utils.data import DataLoader
#d2l.DATA_HUB['hotdog'] = (d2l.DATA_URL + 'hotdog.zip','fba480ffa8aa7e0febbb511d181409f899b9baa5')
#data_dir = d2l.download_extract('hotdog')
data_dir = "dataset/hotdog/hotdog" # 因為我一直下載不了，就手動下載解壓到這個目錄下了
train_imgs = torchvision.datasets.ImageFolder(os.path.join(data_dir, 'train'))
test_imgs = torchvision.datasets.ImageFolder(os.path.join(data_dir, 'test'))
# 使用RGB通道的均值和標準差，以標準化每個通道
normalize = torchvision.transforms.Normalize(
[0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
# 這個是imageNet中資料的均值方差，因為模型在這上面訓練的時候進行了標準化，因此我們也需要標準化
train_augs = torchvision.transforms.Compose([
torchvision.transforms.RandomResizedCrop(224),
torchvision.transforms.RandomHorizontalFlip(),
torchvision.transforms.ToTensor(),
normalize])
test_augs = torchvision.transforms.Compose([
torchvision.transforms.Resize(256),
torchvision.transforms.CenterCrop(224),
torchvision.transforms.ToTensor(),
normalize])
finetune_net = torchvision.models.resnet18(pretrained=True) # 獲取預先訓練的模型
finetune_net.fc = nn.Linear(finetune_net.fc.in_features, 2) # 調整線性分類層
nn.init.xavier_uniform_(finetune_net.fc.weight) # 隨機初始化線性分類層的權重
# 如果param_group=True，輸出層中的模型引數將使用十倍的學習率
def train_fine_tuning(net, learning_rate, batch_size=128, num_epochs=5,
param_group=True):
train_iter = DataLoader(torchvision.datasets.ImageFolder(
os.path.join(data_dir, 'train'), transform=train_augs),
batch_size=batch_size, shuffle=True)
test_iter = DataLoader(torchvision.datasets.ImageFolder(
os.path.join(data_dir, 'test'), transform=test_augs),
batch_size=batch_size)
devices = d2l.try_all_gpus()
loss = nn.CrossEntropyLoss(reduction="none")
if param_group:
params_1x = [param for name, param in net.named_parameters()
if name not in ["fc.weight", "fc.bias"]]
trainer = torch.optim.SGD([{'params': params_1x},
{'params': net.fc.parameters(),
'lr': learning_rate * 10}],
lr=learning_rate, weight_decay=0.001)
else:
trainer = torch.optim.SGD(net.parameters(), lr=learning_rate,
weight_decay=0.001)
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs,
devices)
train_fine_tuning(finetune_net, 5e-5)
plt.show()
結果為：
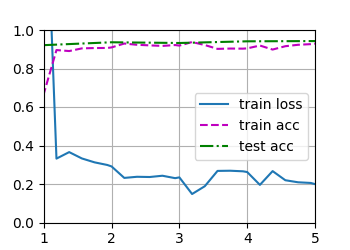
loss 0.200, train acc 0.929, test acc 0.943
188.7 examples/sec on [device(type='cuda', index=0)]
可以看到效果是很好的。
小結：
- 遷移學習將從源資料集中學到的知識「遷移」到目標資料集，微調是遷移學習的常見技巧。
- 除輸出層外，目標模型從源模型中複製所有模型設計及其引數，並根據目標資料集對這些引數進行微調。但是，目標模型的輸出層需要從頭開始訓練。
- 通常，微調引數使用較小的學習率，而從頭開始訓練輸出層可以使用更大的學習率。
實戰Kaggle比賽：影象分類（CIFAR-10)
import collections
import math
import os
import shutil
import pandas as pd
import torch
import torchvision
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
from torch.utils.data import DataLoader
d2l.DATA_HUB['cifar10_tiny'] = (d2l.DATA_URL + 'kaggle_cifar10_tiny.zip',
'2068874e4b9a9f0fb07ebe0ad2b29754449ccacd')
# 如果你使用完整的Kaggle競賽的資料集，設定demo為False
demo = True
if demo:
data_dir = d2l.download_extract('cifar10_tiny')
else:
data_dir = 'dataset/cifar-10/'
# @save
def read_csv_labels(fname):
with open(fname, 'r') as f:
lines = f.readlines()[1:] # 跳過檔案頭一行
tokens = [l.rstrip().split(',') for l in lines]
return dict(((name, label) for name, label in tokens))
#@save
def copyfile(filename, target_dir):
# 將檔案複製到目標路徑，一個類別佔有一個資料夾
os.makedirs(target_dir, exist_ok=True)
shutil.copy(filename, target_dir)
#@save
def reorg_train_valid( data_dir, labels, valid_ratio):
# 該函數將驗證集從原始的訓練集中拆分出來
n = collections.Counter(labels.values()).most_common()[-1][1] # 取出訓練資料集中樣本最少的類別中的樣本數
n_valid_per_label = max(1, math.floor(n * valid_ratio)) # 至少不能小於1
label_count = {}
for train_file in os.listdir(os.path.join(data_dir, 'train')): # 該資料夾下的類別名稱的檔名列表
label = labels[train_file.split(".")[0]]
fname = os.path.join(data_dir, "train", train_file)
copyfile(fname, os.path.join(data_dir, "train_valid_test","train_valid", label))
if label not in label_count or label_count[label] < n_valid_per_label:
copyfile(fname, os.path.join(data_dir, "train_valid_test", "valid", label))
label_count[label] = label_count.get(label,0) + 1
else:
copyfile(fname, os.path.join(data_dir, "train_valid_test", "train", label))
return n_valid_per_label
#@save
def reorg_test(data_dir):
# 在預測期間整理測試集方便讀取
for test_file in os.listdir(os.path.join(data_dir, 'test')):
copyfile(os.path.join(data_dir, 'test', test_file),
os.path.join(data_dir, 'train_valid_test','test','unknown'))
def reorg_cifar10_data(data_dir, valid_ratio):
labels = read_csv_labels(os.path.join(data_dir, 'trainLabels.csv'))
reorg_train_valid( data_dir, labels, valid_ratio)
reorg_test(data_dir)
def get_net():
num_classes = 10
net = d2l.resnet18(num_classes,3)
return net
def train(net, train_iter, valid_iter, num_epochs, lr, wd, devices, lr_period, lr_decay):
# 這裡主要不同是後面兩個引數，就是學習率每經過幾個epoch後就乘以lr_decay來縮小
trainer = torch.optim.SGD(net.parameters(), lr=lr, momentum=0.9, weight_decay=wd)
scheduler = torch.optim.lr_scheduler.StepLR(trainer, lr_period,lr_decay)
# 這個就可以存取trainer中的lr並修改了
num_batches, timer = len(train_iter), d2l.Timer()
legend = ['train loss', 'train acc']
if valid_iter is not None:
legend.append('valid acc')
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],legend=legend)
net = nn.DataParallel(net, device_ids=devices).to(devices[0])
for epoch in range(num_epochs):
net.train()
metric = d2l.Accumulator(3)
for i, (features, labels) in enumerate(train_iter):
timer.start()
l, acc = d2l.train_batch_ch13(net, features, labels,
loss, trainer, devices)
metric.add(l, acc, labels.shape[0])
timer.stop()
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(metric[0] / metric[2], metric[1] / metric[2],
None))
if valid_iter is not None:
valid_acc = d2l.evaluate_accuracy_gpu(net, valid_iter)
animator.add(epoch + 1, (None, None, valid_acc))
scheduler.step() # 更新學習率
print("第{}個epoch已更新完成！".format(epoch+1))
measures = (f'train loss {metric[0] / metric[2]:.3f}, '
f'train acc {metric[1] / metric[2]:.3f}')
if valid_iter is not None:
measures += f', valid acc {valid_acc:.3f}'
print(measures + f'\n{metric[2] * num_epochs / timer.sum():.1f}'
f' examples/sec on {str(devices)}')
if __name__ == '__main__':
labels = read_csv_labels(os.path.join(data_dir, 'trainLabels.csv'))
print("訓練樣本數目為：\t", len(labels))
print("類別數目為：\t", len(set(labels.values())))
batch_size = 32 if demo else 128
valid_ratio = 0.1
reorg_cifar10_data(data_dir, valid_ratio)
# 下面做影象的增廣
transform_train = torchvision.transforms.Compose(
[torchvision.transforms.Resize(40), # 因為原尺寸32，加大到40後再隨機裁剪32的大小
torchvision.transforms.RandomResizedCrop(32, scale=(0.64,1.0), ratio=(1.0,1.0)),
# 裁剪後生成一個面積為原來0.64到1倍大小的正方形（ratio保持不變就是原來的比例）
torchvision.transforms.RandomHorizontalFlip(),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize([0.4914, 0.4822,0.4465],[0.2023,0.1994,0.2010])
# 這是imageNet資料集三個通道的均值和方差
])
transform_test = torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010])
])
train_ds, train_valid_ds = [torchvision.datasets.ImageFolder(
os.path.join(data_dir, "train_valid_test",folder),
transform=transform_train) for folder in ['train','train_valid']]
valid_ds, test_ds = [torchvision.datasets.ImageFolder(
os.path.join(data_dir, "train_valid_test",folder),
transform=transform_test) for folder in ['valid','test']]
train_iter, train_valid_iter = [DataLoader(dataset, batch_size, shuffle=True, drop_last=True)
for dataset in (train_ds, train_valid_ds)] # shuffle隨機打亂
valid_iter = DataLoader(valid_ds, batch_size, shuffle=False, drop_last=True)
test_iter = DataLoader(test_ds, batch_size, shuffle=False, drop_last=False)
loss = nn.CrossEntropyLoss(reduction='none')
devices, num_epochs, lr,wd = d2l.try_all_gpus(), 20, 5e-4, 5e-4
lr_period, lr_decay, net = 4, 0.9, get_net()
train(net, train_iter, valid_iter, num_epochs, lr, wd, devices, lr_period, lr_decay)
plt.show()
# 訓練完，前面是根據驗證集不斷調整引數，調整好了現在要將驗證集加入然後重新按照剛才的引數訓練來預測
net, preds = get_net(), []
train(net, train_valid_iter, None, num_epochs, lr, wd, devices, lr_period, lr_decay)
plt.show()
for X,_ in test_iter:
y_hat = net(X.to(devices[0]))
preds.extend(y_hat.argmax(dim=1).type(torch.int32).cpu().numpy())
sorted_ids = list(range(1,len(test_ds) + 1))
sorted_ids.sort(key=lambda x:str(x))
df = pd.DataFrame({'id':sorted_ids,"label":preds})
df['label'] = df['label'].apply(lambda x : train_valid_ds.classes[x])
df.to_csv("submission_cifar10.csv",index=False)
訓練結果為：
train loss 1.088, train acc 0.609, valid acc 0.391
482.5 examples/sec on [device(type='cuda', index=0)]
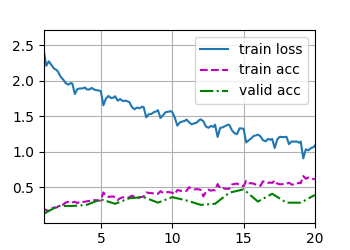
train loss 0.936, train acc 0.653
521.7 examples/sec on [device(type='cuda', index=0)]
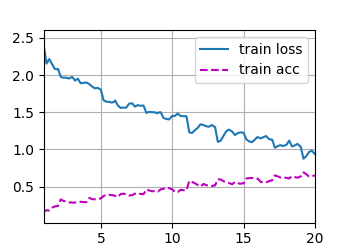
實戰Kaggle比賽：狗的品種識別
import os
import torch
import torchvision
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
# @save
from torch.utils.data import DataLoader
d2l.DATA_HUB['dog_tiny'] = (d2l.DATA_URL + 'kaggle_dog_tiny.zip',
'0cb91d09b814ecdc07b50f31f8dcad3e81d6a86d')
# 如果你使用Kaggle比賽的完整資料集，請將下面的變數更改為False
demo = True
if demo:
data_dir = d2l.download_extract('dog_tiny')
else:
data_dir = os.path.join('dataset', 'dog-breed-identification')
# 這裡同樣是整理資料集，將資料集按照標籤分類到對應的資料夾中
def reorg_dog_data(data_dir, valid_ratio):
labels = d2l.read_csv_labels(os.path.join(data_dir, 'labels.csv'))
d2l.reorg_train_valid(data_dir, labels, valid_ratio) # 這個函數在上個實戰中已經實現過
d2l.reorg_test(data_dir) # 測試集也是一樣
# 載入預訓練好的模型
def get_net(devices):
finetune_net = nn.Sequential() # 一開始是空的
finetune_net.features = torchvision.models.resnet34(pretrained=True) # 新增一個名為特徵的Sequential
# 其內容就是resnet34的整個模型
# 定義一個新的輸出網路，共有120個輸出類別，因為原始的resnet34輸出為1000，因此需要從1000開始
finetune_net.output_new = nn.Sequential(nn.Linear(1000, 256), nn.ReLU(), nn.Linear(256, 120))
# 將模型引數分配給用於計算的CPU或GPU
finetune_net = finetune_net.to(devices[0])
# 特徵提取部分不更新，因為資料集是imageNet的子集
for param in finetune_net.features.parameters():
param.requires_grad = False
return finetune_net
# 用來計算損失
def evaluate_loss(data_iter, net, devices):
l_sum, n = 0.0, 0
for features, labels in data_iter:
features, labels = features.to(devices[0]), labels.to(devices[0])
outputs = net(features)
l = loss(outputs, labels)
l_sum += l.sum()
n += labels.numel()
return (l_sum / n).to('cpu')
# 定義訓練函數
def train(net, train_iter, valid_iter, num_epochs, lr, wd, devices, lr_period,
lr_decay):
# 只訓練小型自定義輸出網路
net = nn.DataParallel(net, device_ids=devices).to(devices[0]) # 多GPU
trainer = torch.optim.SGD((param for param in net.parameters() # 這裡是必須requires_grad為True才訓練
if param.requires_grad), lr=lr, # 也就只有我們剛才新增的MLP
momentum=0.9, weight_decay=wd)
scheduler = torch.optim.lr_scheduler.StepLR(trainer, lr_period, lr_decay)
num_batches, timer = len(train_iter), d2l.Timer()
legend = ['train loss']
if valid_iter is not None:
legend.append('valid loss')
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=legend)
for epoch in range(num_epochs):
metric = d2l.Accumulator(2)
for i, (features, labels) in enumerate(train_iter):
timer.start()
features, labels = features.to(devices[0]), labels.to(devices[0])
trainer.zero_grad()
output = net(features)
l = loss(output, labels).sum()
l.backward()
trainer.step()
metric.add(l, labels.shape[0])
timer.stop()
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(metric[0] / metric[1], None))
measures = f'train loss {metric[0] / metric[1]:.3f}'
if valid_iter is not None:
valid_loss = evaluate_loss(valid_iter, net, devices)
animator.add(epoch + 1, (None, valid_loss.detach().cpu()))
scheduler.step()
if valid_iter is not None:
measures += f', valid loss {valid_loss:.3f}'
print(measures + f'\n{metric[1] * num_epochs / timer.sum():.1f}'
f' examples/sec on {str(devices)}')
if __name__ == '__main__':
batch_size = 32 if demo else 128
valid_ratio = 0.1
reorg_dog_data(data_dir, valid_ratio)
# 進行影象增廣處理
transform_train = torchvision.transforms.Compose([
torchvision.transforms.RandomResizedCrop(224, scale=(0.08, 1.0), ratio=(3.0 / 4.0, 4.0 / 3.0)),
# 隨機裁剪影象，面積為原來的0.08到1之間，並且高寬比控制在3/4到4/3之間，然後縮放到224的大小
torchvision.transforms.RandomHorizontalFlip(),
torchvision.transforms.ColorJitter(brightness=0.4, contrast=0.4, saturation=0.4),
# 隨機改變亮度、對比度和飽和度
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
transform_test = torchvision.transforms.Compose([
torchvision.transforms.Resize(256), # 先縮放的256
# 從影象中心裁切224x224大小的圖片
torchvision.transforms.CenterCrop(224),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
# 讀取資料集
train_ds, train_valid_ds = [torchvision.datasets.ImageFolder(
os.path.join(data_dir, 'train_valid_test', folder),
transform=transform_train) for folder in ['train', 'train_valid']]
valid_ds, test_ds = [torchvision.datasets.ImageFolder(
os.path.join(data_dir, 'train_valid_test', folder),
transform=transform_test) for folder in ['valid', 'test']]
# 建立資料迭代器
train_iter, train_valid_iter = [DataLoader(dataset, batch_size, shuffle=True, drop_last=True)
for dataset in (train_ds, train_valid_ds)]
valid_iter = DataLoader(valid_ds, batch_size, shuffle=False, drop_last=True)
test_iter = DataLoader(test_ds, batch_size, shuffle=False, drop_last=False)
# 損失函數
loss = nn.CrossEntropyLoss(reduction='none')
# 設定引數
devices, num_epochs, lr, wd = d2l.try_all_gpus(), 50, 1e-2, 1e-4
lr_period, lr_decay, net = 10, 0.1, get_net(devices)
train(net, train_iter, valid_iter, num_epochs, lr, wd, devices, lr_period, lr_decay)
plt.show()
# 預測模型
net = get_net(devices)
train(net, train_valid_iter, None, num_epochs, lr, wd, devices, lr_period,
lr_decay)
preds = []
for data, label in test_iter:
output = torch.nn.functional.softmax(net(data.to(devices[0])), dim=0)
# 這裡並不是將最高概率的取出，而是經過softmax將所有概率都放入
preds.extend(output.cpu().detach().numpy())
ids = sorted(os.listdir(os.path.join(data_dir, 'train_valid_test', 'test', 'unknown')))
with open('submission.csv_dog_all', 'w') as f:
f.write('id,' + ','.join(train_valid_ds.classes) + '\n')
for i, output in zip(ids, preds):
f.write(i.split('.')[0] + ',' + ','.join([str(num) for num in output]) + '\n')
目標檢測
目標檢測是對圖片或者視訊中出現的目標物體進行圈出，具體的邊緣框的表達方式有多種，最典型是以下兩種：
- （左上x，左上y，右下x，右下y）
- （左上x，左上y，寬，高）
import torch
from d2l import torch as d2l
from matplotlib import pyplot as plt
d2l.set_figsize()
img = d2l.plt.imread("catdog.jpg")
d2l.plt.imshow(img)
#plt.show()
# @save
def box_corner_to_center(boxes):
# 該函數將框的表示從兩個角轉換為（中間，寬度，高度）的表示方法
x1, y1, x2, y2 = boxes[:, 0], boxes[:, 1], boxes[:, 2], boxes[:, 3]
cx = (x1 + x2) / 2 # 中心
cy = (y1 + y2) / 2
w = x2 - x1 # 寬度
h = y2 - y1 # 高度
boxes = torch.stack((cx, cy, w, h), axis=-1) # 沿著一個新的維度對張量進行拼接，需要張量都是相同的形狀
return boxes
#@save
def box_center_to_corner(boxes):
"""從（中間，寬度，高度）轉換到（左上，右下）"""
cx, cy, w, h = boxes[:, 0], boxes[:, 1], boxes[:, 2], boxes[:, 3]
x1 = cx - 0.5 * w
y1 = cy - 0.5 * h
x2 = cx + 0.5 * w
y2 = cy + 0.5 * h
boxes = torch.stack((x1, y1, x2, y2), axis=-1)
return boxes
dog_bbox, cat_bbox = [60.0, 45.0, 378.0, 516.0], [400.0, 112.0, 655.0, 493.0]
boxes = torch.tensor((dog_bbox, cat_bbox))
print(box_center_to_corner(box_corner_to_center(boxes)) == boxes)
#@save
def bbox_to_rect(bbox, color):
# 將邊界框(左上x,左上y,右下x,右下y)格式轉換成matplotlib格式：
# ((左上x,左上y),寬,高)
return d2l.plt.Rectangle(xy=(bbox[0], bbox[1]), width=bbox[2]-bbox[0], height=bbox[3]-bbox[1],
fill=False, edgecolor=color, linewidth=2)
fig = d2l.plt.imshow(img)
fig.axes.add_patch(bbox_to_rect(dog_bbox,'blue'))
fig.axes.add_patch(bbox_to_rect(cat_bbox,'red'))
plt.show()
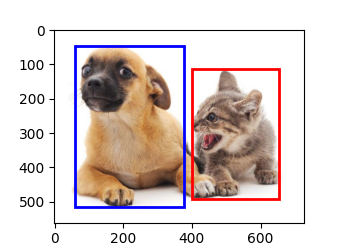
小結：
- 目標檢測不僅可以識別影象中所有感興趣的物體，還能夠識別它們的位置，該位置通常由矩形邊界框表示
- 常用表示方法為(中間，寬度，高度)和(左上，右下)
目標檢測資料集
import os
import pandas as pd
import torch
import torchvision
from d2l import torch as d2l
#@save
from matplotlib import pyplot as plt
from torch.utils.data import DataLoader
d2l.DATA_HUB['banana-detection'] = (
d2l.DATA_URL + 'banana-detection.zip',
'5de26c8fce5ccdea9f91267273464dc968d20d72')
#@save
def read_data_bananas(is_train=True):
# 讀取香蕉檢測資料集中的影象和標籤
data_dir = d2l.download_extract('banana-detection')
csv_fname = os.path.join(data_dir, 'bananas_train' if is_train else 'bananas_val','label.csv')
csv_data = pd.read_csv(csv_fname)
print(csv_data[1:5])
csv_data = csv_data.set_index('img_name') # 將這一列作為索引標籤號
print(csv_data[1:5])
images, targets = [],[]
for img_name ,target in csv_data.iterrows():
images.append(torchvision.io.read_image(os.path.join(data_dir,'bananas_train' if is_train else
'bananas_val','images',f'{img_name}')))
# 這裡的target包含（類別，左上角x，左上角y，右下角x，右下角y），
# 其中所有影象都具有相同的香蕉類（索引為0）
targets.append(list(target))
return images, torch.tensor(targets).unsqueeze(1) / 256
#@save
class BananasDataset(torch.utils.data.Dataset):
"""一個用於載入香蕉檢測資料集的自定義資料集"""
def __init__(self, is_train):
self.features, self.labels = read_data_bananas(is_train)
print('read ' + str(len(self.features)) + (f' training examples' if
is_train else f' validation examples'))
def __getitem__(self, idx):
return self.features[idx].float(), self.labels[idx]
def __len__(self):
return len(self.features)
#@save
def load_data_bananas(batch_size):
"""載入香蕉檢測資料集"""
train_iter = DataLoader(BananasDataset(is_train=True),
batch_size, shuffle=True)
val_iter = DataLoader(BananasDataset(is_train=False),
batch_size)
return train_iter, val_iter
batch_size, edge_size = 32, 256
train_iter, _ = load_data_bananas(batch_size)
batch = next(iter(train_iter))
# 是一個列表，兩個元素都是一個tensor，然後第一個tensor記錄圖片的資訊（批次，通道數目，高，寬）
# 第二個是記錄對應圖片中那些矩形框的位置，（批次，矩形框數目，記錄位置的維度），第三個是一個長度為5的陣列
# 該陣列的第一個元素如果為-1，就代表這個矩形框是非法的，因為我們必須保持矩形框數目相同，而有的圖片中矩形框資料不一樣
# 因此以-1來填充保持大小一樣，後面四個元素就記錄這個矩形框的位置了
print("batch[0].size:\t",batch[0].shape)
print("batch[1].size:\t",batch[1].shape)
imgs = (batch[0][0:10].permute(0,2,3,1)) / 255 # 將維度轉換為（批次，高，寬，通道數目）
axes = d2l.show_images(imgs, 2,5,scale = 2)
for ax, label in zip(axes, batch[1][0:10]):
d2l.show_bboxes(ax, [label[0][1:5] * edge_size], colors=['w'])
plt.show()
其中我對部分地方進行了輸出，方便理解讀入的資料的形式：
img_name label xmin ymin xmax ymax
1 1.png 0 68 175 118 223
2 2.png 0 163 173 218 239
3 3.png 0 48 157 84 201
4 4.png 0 32 34 90 86
label xmin ymin xmax ymax
img_name
1.png 0 68 175 118 223
2.png 0 163 173 218 239
3.png 0 48 157 84 201
4.png 0 32 34 90 86
錨框
目標檢測演演算法通常會在輸入影象中取樣大量的區域，然後判斷這些區域中是否包含我們感興趣的目標，並調整目標邊界從而更準確地預測目標的真實邊框界。
具體的流程為：
- 提出多個被稱為錨框的區域（邊緣框）
- 預測每個錨框裡面是否含有關注的物體
- 如果是，預測從這個錨框到真實邊緣框的偏移
那麼上述過程就存在許多可以進行細究的點。
首先是如何生成多個錨框。
假設輸入影象的高度為h，寬度為w。我們以影象的每個畫素為中心生成不同形狀的錨框：縮放比為\(s\in (0,1]\)，寬高比為\(r>0\)，那麼錨框的寬度和高度分別是\(ws\sqrt{r}、hs/\sqrt{r}\)表達。
那麼如果考慮每個畫素點都隨機應用所有\(s_1,...,s_n\)和\(r_1,...,r_m\)的組合，這樣複雜度為\(whnm\)太高了。因為只考慮：
\[(s_1,r_1),...,(s_1,r_m),(s_2,r_1),..,(s_n,r_1)
\]
因此複雜度為\(wh(n+m-1)\)。
接下來是計算錨框與真實邊緣框的差距。
使用IoU交併比來計算兩個框之間的相似度：
\[IoU=\frac{兩個框相交面積}{兩個相併面積}
\]
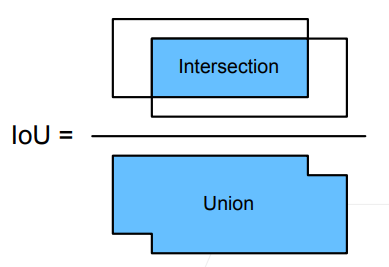
接下來是在訓練資料中標註出錨框。
因為在訓練集中，目標檢測任務和圖片分類任務不同，可以認為每個錨框是一個訓練樣本。而為了訓練這個模型，我們需要知道每個錨框的類別和偏移量標籤，前者是這個錨框是框住了哪一個物件，後者是該錨框相對於該物件的真實邊緣框的偏移量。
那麼我們生成了很多的錨框，可能這會導致每個都去計算的話計算量太大。那麼將真實邊界框進行分配，減少計算量的演演算法為：
- 給定影象，假設真實邊框為\(B_1,...,B_{n_b}\)，生成的錨框為\(A_1,...,A_{n_a}\)，其中\(n_b\leq n_a\)。定義一個矩陣為\(\pmb{X}\in R^{n_a\times n_b}\)，其中第i行第j列的元素為錨框\(A_i\)和真實邊框\(B_j\)之間的IoU。
- 不斷在矩陣中尋找最大值，找到後就將其對應的列和行刪除，得到縮小的矩陣。直到所有的列均刪除，也就是每個真實邊緣框都有對應的最大IoU的錨框匹配。最後剩下\(n_a-n_b\)個錨框。
- 對於剩下的錨框，對於\(A_i\)，找到它和所有真實邊緣框的IoU中最大的那個值，如果值大於閾值，就可以將該真實邊緣框分配給\(A_i\)。完成
標記類別和偏移量。
假設錨框A和其分配到的真實邊緣框B，中心座標分別為\((x_a,y_a)、(x_b,y_b)\)，寬度分別為\(w_a、w_b\)，高度分別為\(h_a、h_b\)，那麼將A的偏移量標記為：
\[(\frac{\frac{x_b-x_a}{w_a} - \mu_x}{\sigma_x},\frac{\frac{y_b-y_a}{h_a} - \mu_y}{\sigma_y},\frac{\log\frac{w_b}{w_a}-\mu_w}{\sigma_w},\frac{\log\frac{h_b}{h_a}-\mu_h}{\sigma_h})
\]
其中\(\mu和\sigma\)取常用值。
使用非極大值抑制(NMS)輸出
經過上述處理，我們剩下的錨框中仍然可能是一個真實邊緣框對應多個錨框，那麼可能這些錨框是很相似的。NMS的處理就是將這些對應同一個真實邊緣框的多個錨框，它們分別對自己框內的物體做預測，得到預測為真實邊緣框內物體的置信度，然後選擇最大的置信度對應的錨框\(A_i\)，然後將其他與\(A_i\)的IoU值大於閾值的錨框刪除掉。重複上述過程指導所有錨框要麼被選中，要麼被去掉。
區域折積神經網路（R-CNN）系列
首先是最原始的R-CNN。
簡而言之，R-CNN首先從輸入影象中選取若干提議區域（錨框就是一種，可理解為選取錨框），並標註它們的類別和邊界框（如與真實框的偏移量），然後用折積神經網路對每個提議區域進行前向傳播以抽取其特徵，然後用每個提議區域的特徵來預測類別和邊界框。
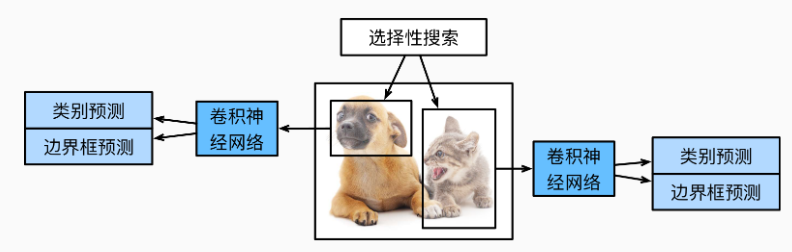
具體的步驟為：
- 對輸入影象使用選擇性搜尋來選取多個高質量的提議區域（錨框）。這些錨框通常是在多個尺度下選取的，具有不同的大小和形狀。每個提議區域都將被標註類別和真實邊界框。
- 選擇一個預訓練的折積神經網路，並將其在輸出層之前截斷。將每個提議區域變形為網路需要的輸入尺寸，並通過前向傳播輸出抽取的提議區域特徵。
- 將每個提議區域的特徵連同其標註的類別作為一個樣本。訓練多個支援向量機對目標分類，其中每個支援向量機用來判斷樣本是否屬於某一個類別。
- 將每個提議區域的特徵連同其標註的邊界框作為一個樣本，訓練線性迴歸模型來預測真實邊界框。
R-CNN模型通過預訓練的折積神經網路有效地抽取了影象特徵，但是速度很慢，原因在於對每個提議區域都進行了折積的前向傳播。
Fast R-CNN
R-CNN的主要效能瓶頸在於，對每個提議區域，折積神經網路的前向傳播是獨立的，而沒有共用計算。 由於這些區域通常有重疊，獨立的特徵抽取會導致重複的計算。 Fast R-CNN對R-CNN的主要改進之一，是僅在整張圖象上執行折積神經網路的前向傳播。
具體步驟為：
- 對整張影象進行折積神經網路的特徵提取，並且該網路也會參與訓練。設CNN的輸出為\(1\times c \times h_1 \times w_1\)
- 假設選擇性搜尋生成了\(n\)個提議區域，那麼這些區域就按照在原始影象中位置的比例，去CNN輸出的特徵影象中相同位置的比例，標出形狀各異的興趣區域。
- 然後這些形狀各異的興趣區域需要經過興趣區域池化層RoI，它可以對每個區域的輸出形狀直接指定。其將折積神經網路的輸出和提議區域作為輸入，輸出連結後的各個提議區域抽取的特徵，形狀為\(n \times c \times h_2 \times w_2\)
- 通過全連線層將輸出形狀變換為\(n\times d\)，d取決於模型設計
- 預測這n個提議區域中每個區域的類別和邊界框。在預測時將全連線層的輸出分類轉換為形狀為\(n\times q\)(q為類別數目)的輸出和形狀為\(n \times 4\)的輸出（真實標記框需要用4個數位表達）的輸出
RoI的特點在於可以自己指定輸出的形狀。例如指定輸出為\(h_2、w_2\)，對於任何形狀為\(h \times w\)的興趣區域視窗，該視窗會被劃分為\(h_2 \times w_2\)個子視窗網路，其中每個子視窗大小約為\((h/h_2)\times (w/w_2)\)。
Faster R-CNN
為了較精確地檢測目標結果，Fast R-CNN模型通常需要在選擇性搜尋中生成大量的提議區域。而Faster R-CNN提出用區域提議網路（神經網路）來代替選擇性搜尋，從而減少提議區域的生成數量。
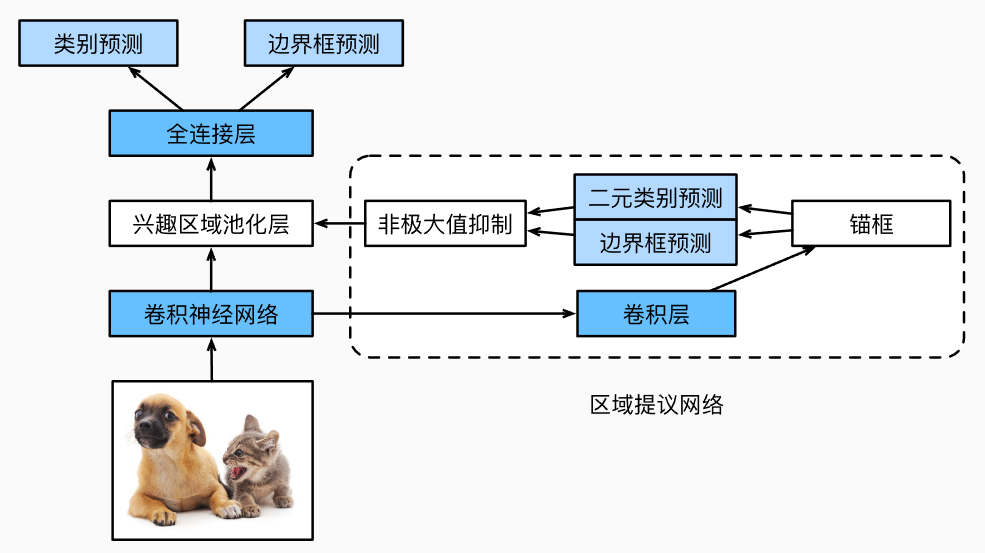
除了區域提議網路外，其他都與Fast R-CNN相同，因此這裡只介紹區域提議網路流程：
- 使用padding=1的\(3\times 3\) 的折積層將折積神經網路的輸出進行處理，設輸出通道為c。因此折積神經網路為影象抽取的特徵圖中的每個單元均得到一個長度為c的新特徵（因為該折積層不會改變高寬，因此相當於每個特徵圖中的畫素點都得到一個長度為c的新特徵）
- 以特徵圖的每個畫素為中心，生成多個不同大小和高寬比的錨框並標註
- 使用錨框中心畫素的長度為c的特徵，分別去預測該錨框的二元類別（是目標還是背景）和邊界框
- 使用非極大值抑制，從預測類別為目標的預測邊界框中移除相似的結果。最終輸出的預測邊界框即是興趣區域匯聚層所需的提議區域。
值得注意的是，區域提議網路也是跟模型一起訓練的。
Mask R-CNN
如果在訓練集中還標註了每個目標在影象上的畫素級位置，那麼Mask R-CNN能夠有效地利用這些詳盡的標註資訊進一步提升目標檢測的精度。
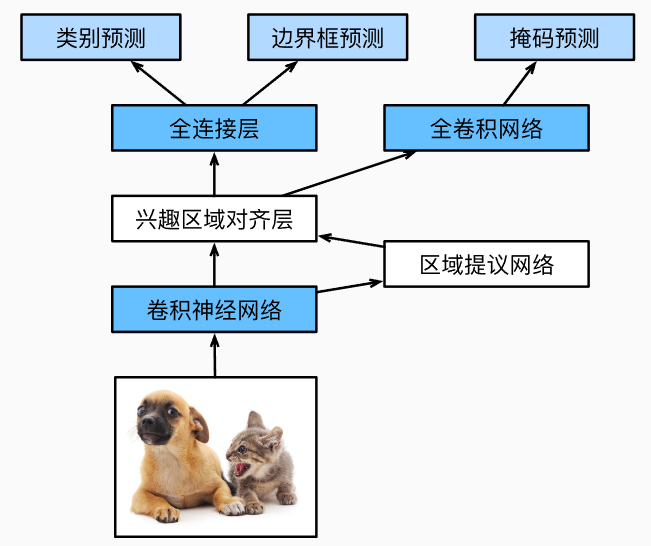
它首先是將RoI層轉換為興趣區域對齊層，因為之間劃分的時候畫素會取整，這樣會導致偏移，這在以畫素為單元的Mask R-CNN中行不通，因此相當於它將不能夠平分的畫素，進行細化，例如\(3\times 3\)要輸出\(2\times 2\)，那麼最中間的畫素點就需要繼續劃分成4個小畫素點，可以採用各種方法去分配取值。另外一個部分是掩碼預測將在後續補充。
小結：
- R-CNN對影象選取若干提議區域，使用折積神經網路對每個提議區域執行前向傳播以抽取其特徵，然後再用這些特徵來預測提議區域的類別和邊界框。
- Fast R-CNN對R-CNN的一個主要改進：只對整個影象做折積神經網路的前向傳播。它還引入了興趣區域匯聚層，從而為具有不同形狀的興趣區域抽取相同形狀的特徵。
- Faster R-CNN將Fast R-CNN中使用的選擇性搜尋替換為參與訓練的區域提議網路，這樣後者可以在減少提議區域數量的情況下仍保證目標檢測的精度。
- Mask R-CNN在Faster R-CNN的基礎上引入了一個全折積網路，從而藉助目標的畫素級位置進一步提升目標檢測的精度。
單發多框檢測（SSD）
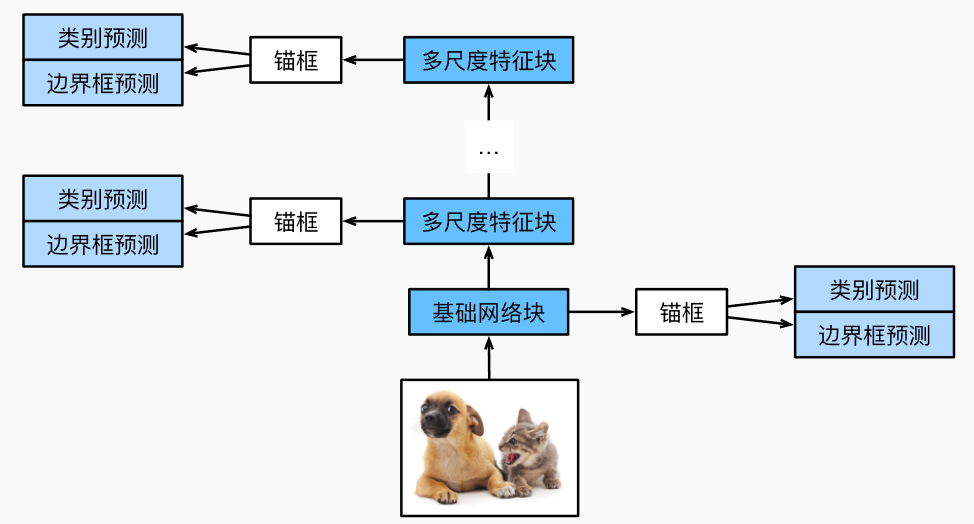
如上圖所示，SSD主要由基礎網路塊，以及幾個多尺度特徵塊構成。
基礎網路塊的主要作用是從輸入影象中提取特徵，並且通常讓其輸出的高和寬比較大，這樣它的輸出用於去生成錨框時，就可以用來標註一些原圖中尺寸比較小的物體。然後多尺度特徵塊將上一層提供的特徵圖的高和寬減小（如減半）這樣相同的錨框大小，就具有更大的感受野，因此後面的錨框將多用於檢測原圖中較大的物體。
這裡稍微補充一下YOLO(you only look ones你只看一次)的思想，因為SSD中錨框大量重疊，因此浪費了很多計算。那麼YOLO將圖片均勻分成\(S\times S\)個錨框，每個錨框就需要預測圖片中已知的B個邊緣框，這樣可以減小錨框數量。
小結：
- 單發多框檢測是一種多尺度目標檢測模型。基於基礎網路塊和各個多尺度特徵塊，單發多框檢測生成不同數量和不同大小的錨框，並通過預測這些錨框的類別和偏移量檢測不同大小的目標。
- 在訓練單發多框檢測模型時，損失函數是根據錨框的類別和偏移量的預測及標註值計算得出的。
迴圈神經網路
序列模型
在現實生活中很多資料都是有時序結構的，那麼對於時序結構的研究也是必要的。
一般對於時序結構而言，在第t個時間點的觀察值\(x_t\)是與前面t-1個時刻的觀察值有關的，但反過來在現實中不一定可行，即：
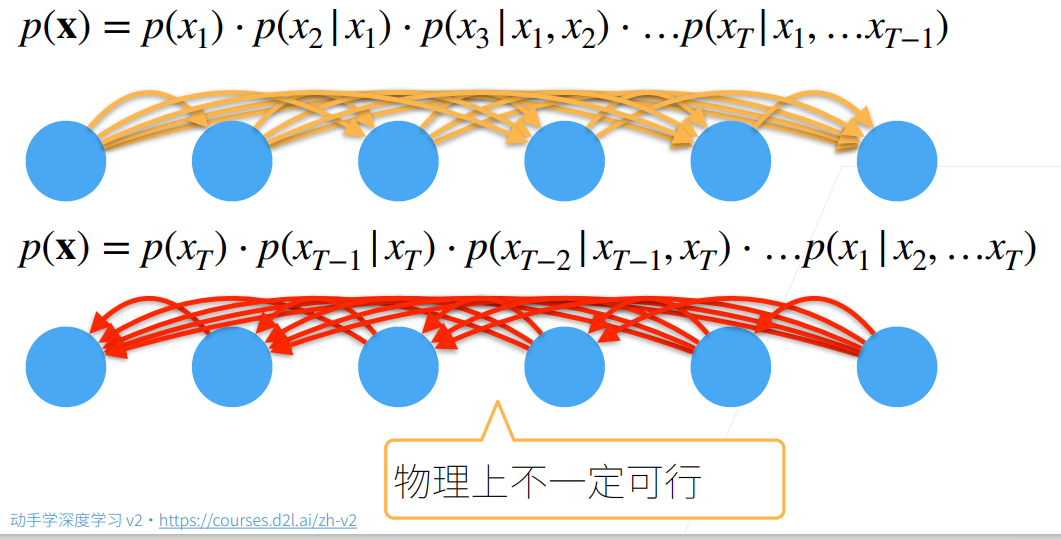
那麼我們對條件概率進行建模，即：
那麼如果能夠學習到模型f，及概率計算方法p，就可以進行預測了。
那麼針對這個問題，有兩種比較常見的研究方法：
馬爾科夫假設：
因為前面我們的敘述是當前時刻的觀察值跟前面所有時刻的觀察值相關，那麼馬爾科夫假設就是假定當前資料只和過去\(\tau\)個資料點相關，這樣函數f的輸入就從不定長轉換為了定長，因此就方便很多：
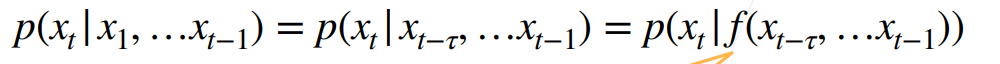
那麼就可以用一個簡單的MLP來實現。
潛變數模型：
即引入潛變數\(h_t\)來表示過去資訊\(h_t=f(x_1,...,x_{t-1})\)，那麼\(x_t=p(x_t \mid h_t)\)：
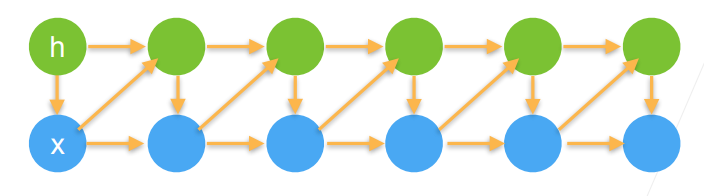
具體老師通過了一個小例子來為我們展示了訓練以及預測：
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
T = 1000 # 總共產生1000個點
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,)) # 加上噪音
# d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
tau = 4
features = torch.zeros((T - tau, tau)) # 因為前tau個之間沒有tau個可以作為輸入
for i in range(tau):
features[:, i] = x[i: T - tau + i] # 例如第0列就是每個資料的前面第4個
labels = x[tau:].reshape((-1, 1)) # 從第4個往後都是前面tau個造成的輸出了
batch_size, n_train = 16, 600
# 用前600個樣本來訓練，然後後面400個完成預測任務
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)
# 初始化網路權重的函數
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
# 一個簡單的多層感知機
def get_net():
net = nn.Sequential(nn.Linear(4, 10),
nn.ReLU(),
nn.Linear(10, 1))
net.apply(init_weights)
return net
loss = nn.MSELoss(reduction='none')
def train(net, train_iter, loss, epochs, lr):
trainer = torch.optim.Adam(net.parameters(), lr)
for epoch in range(epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.sum().backward()
trainer.step()
print(f'epoch {epoch + 1}, '
f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net, train_iter, loss, 5, 0.01)
onestep_preds = net(features)
# 單步預測，就是每次都給定4個真實值來讓你預測下一個
# 注意這裡採用detach是將本來含有梯度的變數，複製一個不含有梯度，不過都是指向同一個數值
# 不含有梯度是因為畫圖不需要計算梯度，防止在畫圖中發生計算過程而改變梯度
d2l.plot([time, time[tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
'x', legend=['data', '1-step preds'], xlim=[1, 1000],figsize=(6, 3))
plt.show()
# 多步預測，只知道600個，然後可以結合真實資料預測到604個，那麼後面都是靠預測值來預測
multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
multistep_preds[i] = net(multistep_preds[i - tau:i].reshape((1, -1)))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy(),
multistep_preds[n_train + tau:].detach().numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))
plt.show()
max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i（i<tau）是來自x的觀測，其時間步從（i）到（i+T-tau-max_steps+1）
for i in range(tau):
features[:, i] = x[i: i + T - tau - max_steps + 1]
# 列i（i>=tau）是來自（i-tau+1）步的預測，其時間步從（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):
features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
figsize=(6, 3))
plt.show()
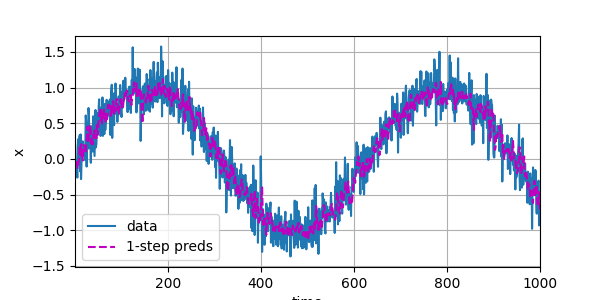
可以看到單步預測的結果還是很精確的。
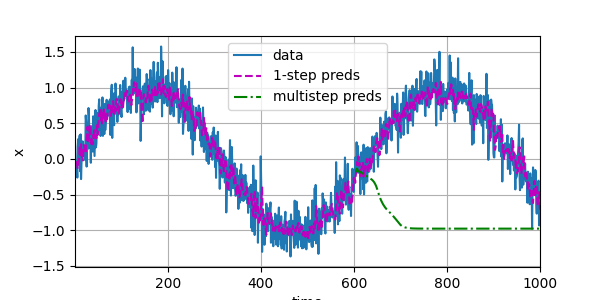
但是在多步預測時，我們如果只給前面600個資料點，然後讓其預測後面400個，就結果差的很離譜
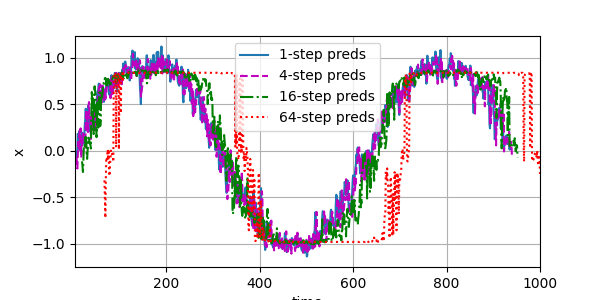
可以看到，多步預測為1，4,16的結果都還算可以，但是增加到64時就出現了明顯的差異。
小結：
- 時序模型中，當前資料跟之前觀察到的資料相關
- 自迴歸模型使用自身過去資料來預測未來
- 馬爾科夫模型假設當前只跟最近少數資料相關，從而簡化模型
- 潛變數模型使用潛變數來概括歷史資訊
文字預處理
該章節主要是介紹了對於一個簡單文字檔案的處理，生成可以用來使用的資料集
import collections
import re
from d2l import torch as d2l
# @save
d2l.DATA_HUB['time_machine'] = (d2l.DATA_URL + 'timemachine.txt',
'090b5e7e70c295757f55df93cb0a180b9691891a')
# 下載資料集
def read_time_machine():
with open(d2l.download('time_machine'), 'r') as f:
lines = f.readlines()
return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]
# 就是將除了A-Z和a-z，還有空格，其他的符號都去掉，再去掉回車，再轉成小寫
lines = read_time_machine()
print(f'# 文字總行數: {len(lines)}')
print(lines[0])
print(lines[10])
def tokenize(lines, token='word'): # @save
if token == 'word':
return [line.split() for line in lines]
elif token == 'char':
return [list(line) for line in lines]
else:
print('錯誤：未知詞元型別：' + token)
tokens = tokenize(lines)
for i in range(11):
print(tokens[i])
def count_corpus(tokens): # @save
"""統計詞元的頻率"""
# 這裡的tokens是1D列表或2D列表
if len(tokens) == 0 or isinstance(tokens[0], list):
# 所有單詞都展開成一個列表
tokens = [token for line in tokens for token in line]
return collections.Counter(tokens)
class Vocab:
def __init__(self, tokens=None, min_freq=0, reserved_tokens=None):
if tokens is None:
tokens = []
if reserved_tokens is None:
reserved_tokens = []
# 按照出現的頻率來進行排序
counter = count_corpus(tokens)
self._token_freqs = sorted(counter.items(), key=lambda x: x[1],
reverse=True)
# 按照出現頻率從大到小排序
# 未知詞元索引在0，包括出現頻率太少，還有句子起始和結尾的標誌
self.idx_to_token = ['<unk>'] + reserved_tokens
self.token_to_idx = {token: idx for idx, token in enumerate(self.idx_to_token)}
for token, freq in self._token_freqs:
if freq < min_freq:
break
if token not in self.token_to_idx:
self.idx_to_token.append(token)
self.token_to_idx[token] = len(self.idx_to_token) - 1
# 不斷新增進去詞彙並建立和位置之間的索引關係
def __len__(self):
return len(self.idx_to_token)
@property
def unk(self): # 未知詞元的索引為0，裝飾器，可以直接self.unk，不用加括號
return 0
def __getitem__(self, tokens):
if not isinstance(tokens, (list, tuple)): # 如果是單個
return self.token_to_idx.get(tokens, self.unk)
return [self.__getitem__(token) for token in tokens] # 如果是多個
def to_tokens(self, indices):
if not isinstance(indices, (list, tuple)):
return self.idx_to_token[indices] # 從索引到單詞
return [self.idx_to_token[index] for index in indices]
@property
def token_freqs(self):
return self._token_freqs
vocab = Vocab(tokens)
print(list(vocab.token_to_idx.items())[:10])
def load_corpus_time_machine(max_tokens=-1): # @save
"""返回時光機器資料集的詞元索引列表和詞表"""
lines = read_time_machine()
tokens = tokenize(lines, 'char')
vocab = Vocab(tokens)
# 因為時光機器資料集中的每個文字行不一定是一個句子或一個段落，
# 所以將所有文字行展平到一個列表中
corpus = [vocab[token] for line in tokens for token in line]
if max_tokens > 0:
corpus = corpus[:max_tokens]
return corpus, vocab
corpus, vocab = load_corpus_time_machine()
len(corpus), len(vocab)
語言模型和資料集
語言模型是指，給定文字序列\(x_1,...,x_T\)，其目標是估計聯合概率\(p(x_1,...,x_T)\)，也就是該文字序列出現的概率。
那麼假設序列長度為2，那我們可以使用計數的方法，簡單計算為：
\[p(x,x^{\prime})=p(x)p(x^{\prime}\mid x)=\frac{n(x)}{n_{all}}\frac{n(x,x^{\prime})}{n(x)}
\]
那麼繼續拓展序列長度也可以採用類似的計數方法。
但是如果序列長度太長，如果文字量不夠大的情況下可能會出現\(n(x_1,...,x_T)\leq 1\)的情況，那麼就可以用馬爾科夫假設來緩解這個問題：
- 一元語法：\(p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2)p(x_3)p(x_4)\)
- 二元語法：\(p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2\mid x_1)p(x_3\mid x_2)p(x_4\mid x_3)\)
- 三元語法：\(p(x_1,x_2,x_3,x_4)=p(x_1)p(x_2\mid x_1)p(x_3\mid x_1,x_2)p(x_4\mid x_2,x_3)\)
程式碼為：
import random
import torch
from d2l import torch as d2l
from matplotlib import pyplot as plt
tokens = d2l.tokenize(d2l.read_time_machine())
# 因為每個文字行不一定是一個句子或一個段落，因此我們把所有文字行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus) # 計算頻率得到的詞彙列表
freqs = [freq for token, freq in vocab.token_freqs] # 將頻率變化畫出來
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)', xscale='log', yscale='log')
plt.show() # 以上這是單個單詞的情況
# 我們來看看連續的兩個單詞和三個單詞的情況，即二元語法和三元語法
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
trigram_tokens = [triple for triple in zip(corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
ylabel='frequency: n(x)', xscale='log', yscale='log',
legend=['unigram', 'bigram', 'trigram'])
plt.show() # 畫出來對比
# 下面我們對一個很長的文字序列，隨機在上面取樣得到我們指定長度的子序列，方便我們輸入到模型中
def seq_data_iter_random(corpus, batch_size, num_steps): # @save
"""使用隨機抽樣生成一個小批次子序列"""
# 從隨機偏移量開始對序列進行分割區，隨機範圍包括num_steps-1
corpus = corpus[random.randint(0, num_steps - 1):]
# 因為長度為num_steps是肯定的，那我們如果每次都從0開始，那麼例如2-7這種就得不到
# 因此每次都隨機的初始點開始就可以保證我們能夠取樣得到不同的資料
# 減去1，是因為我們需要考慮標籤
num_subseqs = (len(corpus) - 1) // num_steps
# 長度為num_steps的子序列的起始索引
initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
# 在隨機抽樣的迭代過程中，
# 來自兩個相鄰的、隨機的、小批次中的子序列不一定在原始序列上相鄰
random.shuffle(initial_indices)
def data(pos):
# 返回從pos位置開始的長度為num_steps的序列
return corpus[pos: pos + num_steps]
num_batches = num_subseqs // batch_size
for i in range(0, batch_size * num_batches, batch_size):
# 在這裡，initial_indices包含子序列的隨機起始索引
initial_indices_per_batch = initial_indices[i: i + batch_size]
X = [data(j) for j in initial_indices_per_batch]
Y = [data(j + 1) for j in initial_indices_per_batch]
# 這裡解釋一下，一開始我認為應該輸入序列x之後我們要輸出x之後的下一個單詞，因此認為y應該為長度為1
# 但是實際上在訓練時我們並不是5個丟進去，然後生成1個出來
# 我們是丟進去第一個，然後生成第二個，然後結合1,2的真實標籤，去預測第三個，以此類推
# 直到後面結合5個去預測第6個
yield torch.tensor(X), torch.tensor(Y)
# 這個函數是讓相鄰兩個小批次中的子序列在原始序列上是相鄰的
def seq_data_iter_sequential(corpus, batch_size, num_steps): # @save
"""使用順序分割區生成一個小批次子序列"""
# 從隨機偏移量開始劃分序列
offset = random.randint(0, num_steps)
num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
Xs = torch.tensor(corpus[offset: offset + num_tokens])
Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
num_batches = Xs.shape[1] // num_steps
for i in range(0, num_steps * num_batches, num_steps):
X = Xs[:, i: i + num_steps]
Y = Ys[:, i: i + num_steps]
yield X, Y
class SeqDataLoader: # @save
"""載入序列資料的迭代器"""
def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
if use_random_iter:
self.data_iter_fn = d2l.seq_data_iter_random
else:
self.data_iter_fn = d2l.seq_data_iter_sequential
self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
self.batch_size, self.num_steps = batch_size, num_steps
def __iter__(self):
return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)
# 封裝，同時返回資料迭代器和詞彙表
def load_data_time_machine(batch_size, num_steps, #@save
use_random_iter=False, max_tokens=10000):
"""返回時光機器資料集的迭代器和詞表"""
data_iter = SeqDataLoader(
batch_size, num_steps, use_random_iter, max_tokens)
return data_iter, data_iter.vocab
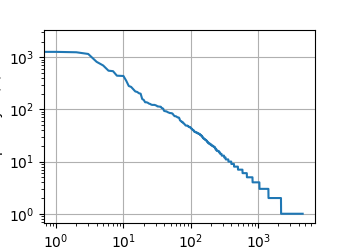
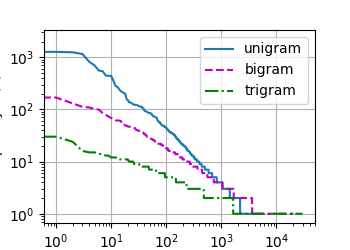
迴圈神經網路
其模型可以用下圖來表示：
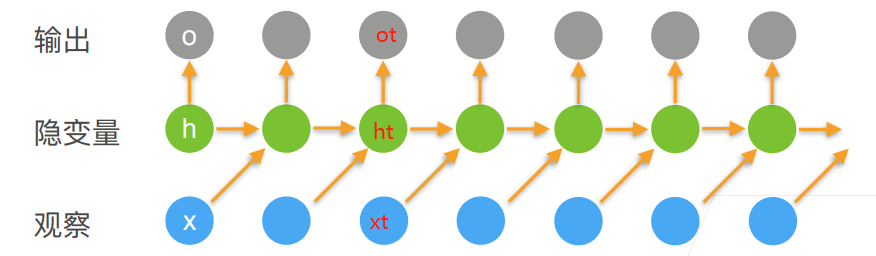
即中間的隱變數，是用來捕獲並保留數序列直到其當前時間步的歷史資訊，其內部原理為：
- 更新隱藏狀態：\(\pmb{h}_t=\phi(\pmb{W}_{hh}\pmb{h}_{t-1}+\pmb{W}_{hx}\pmb{x}_{t-1}+\pmb{b}_h)\)
- 輸出：\(\pmb{o}_t=(\pmb{W}_{ho}\pmb{h}_t+\pmb{b}_o)\)
例如在\(t_1\)時刻輸入\(x_1=\)"你"，那麼我們希望它能夠能夠計算得到\(h_1\)並得到輸出\(o_1\)="好"，然後接下來輸入為\(x_2\)="好"，我們希望\(o_2\)="世"等等。
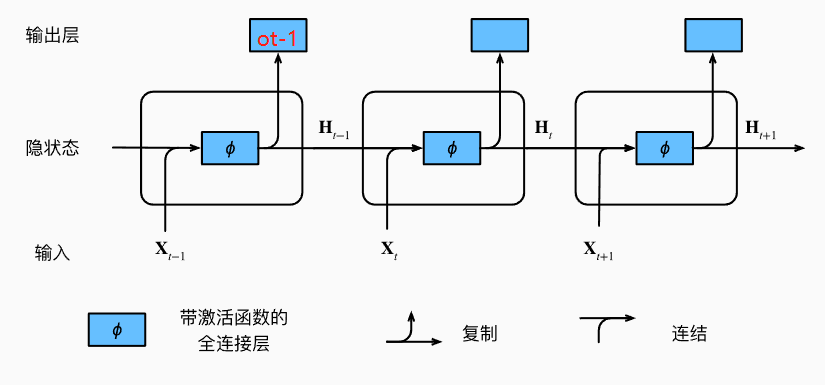
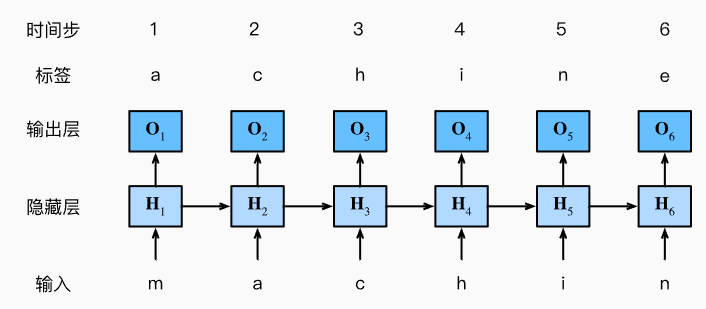
而衡量一個句子的質量，使用的是困惑度，其內部使用平均交叉熵來實現：
\[\pi=\frac{1}{n}\sum_{i=1}^n-\log p(x_t\mid x_{t-1},...,x_1)
\]
注意這裡指的是根據現有已知的\(x_{1},...,x_{t-1}\)的情況（都是真實標籤），我們能夠預測出正確結果\(x_t\)的概率，那麼如果每次都能夠正確預測，就是p=1，那麼log=0。而常見的是用\(\exp(\pi)\)來表達，因此1代表完美，無窮大為最差情況。
下一個知識點是梯度裁剪。
為了防止在迭代過程中計算T個時間步上的梯度時由於不斷疊加而產生的數值不穩定的情況，而引入梯度裁剪：將所有層的梯度拼成一個向量g，那麼如果該向量的L2範數超過了設定值\(\theta\)就將其進行修正，修正為\(\theta\)值，即：
\[\pmb{g}\leftarrow \min (1,\frac{\theta}{\Vert \pmb{g} \Vert})\pmb{g}
\]
RNN有非常多的應用場景：
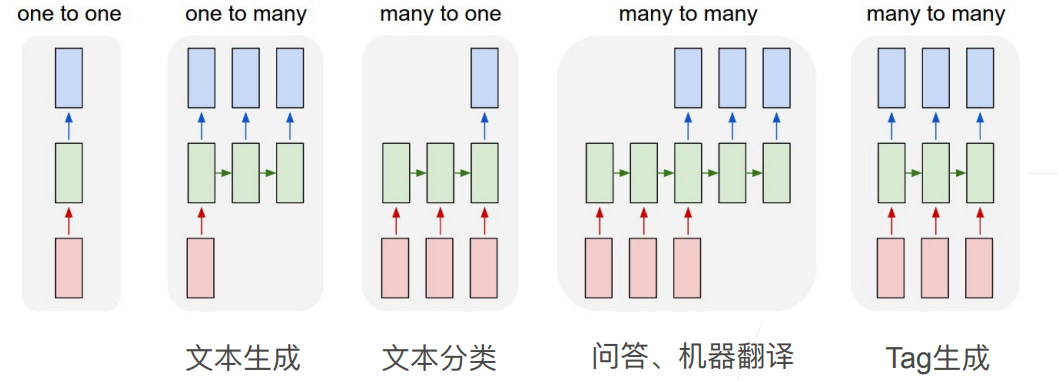
小結：
- RNN的輸出取決於當前輸入和前一時刻的隱變數
- 應用到語言模型中時，RNN根據當前詞預測下一次時刻詞
- 通常使用困惑度來衡量語言模型的好壞
RNN的從零開始實現
完成程式碼如下，需要注意的地方和講解的地方都在註釋中了。
import math
import torch
from matplotlib import pyplot as plt
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 接下來引入獨熱編碼的使用
# print(F.one_hot(torch.tensor([0, 2]), len(vocab)))
# 第一個引數0和2，代表我有兩個編碼，第一個編碼在0的位置取1，第二個在2的位置取1，而長度就是第二個引數
# 而我們每次取樣得到都是批次大小*時間步數，將每個取值（標量）轉換為獨熱編碼就是三維
# 批次大小*時間步數*獨熱編碼，那為了方便，我們將維度轉換為時間步數*批次大小再去變成獨熱編碼
# 這樣每個時刻的數值就連在一起了方便使用，如下：
X = torch.arange(10).reshape((2, 5)) # 批次為2，時間步長為5
# print(F.one_hot(X.T, 28).shape) # 輸出為5,2,28
# 初始化模型引數
def get_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
# 因為輸入是一個字元，就是1個獨特編碼，輸出是預測的下一個字元也是獨熱編碼，因此長度都是獨特編碼的長度
def normal(shape):
return torch.randn(size=shape, device=device) * 0.01
# 隱藏層引數
W_xh = normal((num_inputs, num_hiddens))
W_hh = normal((num_hiddens, num_hiddens))
b_h = torch.zeros(num_hiddens, device=device)
# 輸出層引數
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True) # 我們後面要計算梯度
return params
# 下面是對RNN模型的定義
# 定義初始隱藏層的狀態
def init_rnn_state(batch_size, num_hiddens, device):
# 這裡用元組的原因是為了和後面LSTM統一
return (torch.zeros((batch_size, num_hiddens), device=device), )
def rnn(inputs, state, params):
# inputs的形狀：(時間步數量，批次大小，詞表大小)
W_xh, W_hh, b_h, W_hq, b_q = params
H, = state # 注意state是元組，第二個引數我們暫時不要，所有不用接受，但是要有逗號，否則H是元組
outputs = []
# X的形狀：(批次大小，詞表大小)，這就是我們前面轉置的原因，方便對同一時間步的輸入做預測
for X in inputs:
H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h) # 更新H
Y = torch.mm(H, W_hq) + b_q # 對Y做出預測
outputs.append(Y) # 這裡outputs是陣列，長度為時間步數量，每個元素都是批次大小*詞表大小
# 那個下面對output進行堆疊，就是將時間步維度去掉，行數為（時間步*批次大小），列為詞表大小
return torch.cat(outputs, dim=0), (H,)
# 用類來封裝這些函數
class RNNModelScratch: #@save
"""從零開始實現的迴圈神經網路模型"""
def __init__(self, vocab_size, num_hiddens, device,get_params, init_state, forward_fn):
self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
self.params = get_params(vocab_size, num_hiddens, device)
# 下面這兩個其實是函數，第一個就是剛才初始化隱狀態的函數，第二個就是rnn函數進行前向計算
self.init_state, self.forward_fn = init_state, forward_fn
def __call__(self, X, state):
X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
return self.forward_fn(X, state, self.params) # 進行前向計算後返回
def begin_state(self, batch_size, device):
return self.init_state(batch_size, self.num_hiddens, device)
# 檢查輸出是否具有正確的形狀
num_hiddens = 512
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
init_rnn_state, rnn)
state = net.begin_state(X.shape[0], d2l.try_gpu())
Y, new_state = net(X.to(d2l.try_gpu()), state)
print(Y.shape, "\n",len(new_state),"\n", new_state[0].shape)
# 定義預測函數
def predict_ch8(prefix, num_preds, net, vocab, device): #@save
"""在prefix後面生成新字元"""
# prefix是使用者提供的一個包含多個字元的字串
state = net.begin_state(batch_size=1, device=device)
outputs = [vocab[prefix[0]]] # 將其第一個字元轉換為數位放入其中
get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
# 上是一個匿名函數，可以在每次outputs更新後都呼叫outputs的最後一個元素
for y in prefix[1:]: # 預熱期，此時不做預測，我們用這些字元不斷來更新state
_, state = net(get_input(), state)
outputs.append(vocab[y]) # 將下一個待作為輸入的轉換為數位進入
for _ in range(num_preds): # 預測num_preds步
y, state = net(get_input(), state) # 預測並更新state
outputs.append(int(y.argmax(dim=1).reshape(1))) # 這就是將預測的放入，並作為下一次的輸入
return ''.join([vocab.idx_to_token[i] for i in outputs]) # 拼接成字元
print(predict_ch8('time traveller ', 10, net, vocab, d2l.try_gpu())) # 看看效果
# 梯度裁剪
def grad_clipping(net, theta): #@save
"""裁剪梯度"""
if isinstance(net, nn.Module):
params = [p for p in net.parameters() if p.requires_grad]
# 取出那些需要更新的梯度
else:
params = net.params
norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
if norm > theta:
for param in params:
param.grad[:] *= theta / norm # 對梯度進行修剪
# 訓練模型
#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
"""訓練網路一個迭代週期（定義見第8章）"""
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # 訓練損失之和,詞元數量
for X, Y in train_iter:
if state is None or use_random_iter:
# 如果用的是打亂的，那麼後一個小批次和前一個小批次的樣本之間並不是連線在一起的
# 那麼它們的隱變數不存在關係，所以必須初始化
# 在第一次迭代或使用隨機抽樣時初始化state
state = net.begin_state(batch_size=X.shape[0], device=device)
else: # 否則的話，我們就可以沿用上次計算完的隱變數，只不過detach是斷掉鏈式求導，我們現在隱變數是數值了，跟之前的沒有關係了
if isinstance(net, nn.Module) and not isinstance(state, tuple):
# state對於nn.GRU是個張量，這部分可以認為我們將state變換為常數
# 那麼梯度更新時就不會再和前面批次的梯度進行相乘，這裡就直接斷掉梯度的鏈式法則了
state.detach_()
else:
# state對於nn.LSTM或對於我們從零開始實現的模型是個張量，這部分在後面有用
for s in state:
s.detach_()
y = Y.T.reshape(-1)
X, y = X.to(device), y.to(device)
y_hat, state = net(X, state)
l = loss(y_hat, y.long()).mean()
if isinstance(updater, torch.optim.Optimizer):
updater.zero_grad() # 清空梯度
l.backward()
grad_clipping(net, 1)
updater.step() # 更新引數
else:
l.backward()
grad_clipping(net, 1)
# 因為已經呼叫了mean函數
updater(batch_size=1)
metric.add(l * y.numel(), y.numel())
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()
#@save
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,use_random_iter=False):
"""訓練模型（定義見第8章）"""
loss = nn.CrossEntropyLoss()
animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
legend=['train'], xlim=[10, num_epochs])
# 初始化
if isinstance(net, nn.Module):
updater = torch.optim.SGD(net.parameters(), lr)
else:
updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device) # 預測函數
# 訓練和預測
for epoch in range(num_epochs):
ppl, speed = train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter)
if (epoch + 1) % 10 == 0:
print(predict('time traveller'))
animator.add(epoch + 1, [ppl])
print(f'困惑度 {ppl:.1f}, {speed:.1f} 詞元/秒 {str(device)}')
print(predict('time traveller'))
print(predict('traveller'))
# 順序取樣
num_epochs, lr = 500, 1
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())
plt.show()
# 隨機採用
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,init_rnn_state, rnn)
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),use_random_iter=True)
plt.show()
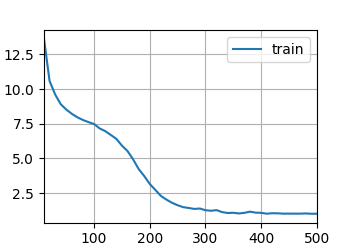
困惑度 1.0, 50189.8 詞元/秒 cuda:0
time traveller for so it will be convenient to speak of himwas e
traveller with a slight accession ofcheerfulness really thi
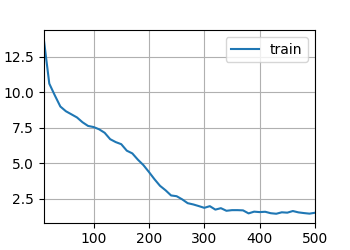
困惑度 1.5, 47149.4 詞元/秒 cuda:0
time traveller proceeded anyreal body must have extension in fou
traveller held in his hand was a glitteringmetallic furmime
小結：
- 我們可以訓練一個基於迴圈神經網路的字元級語言模型，根據使用者提供的文字的字首 生成後續文字
- 一個簡單的迴圈神經網路語言模型包括輸入編碼、迴圈神經網路模型和輸出生成
- 迴圈神經網路模型在訓練以前需要初始化狀態，不過隨機抽樣和順序劃分使用初始化方法不同
- 當使用順序劃分時，我們需要分離梯度以減少計算量（detach）
- 在進行任何預測之前，模型通過預熱期進行自我更新（獲得比初始值更好的隱狀態，訓練只是修改引數，並沒有改狀態）
- 梯度裁剪可以防止梯度爆炸，但不能應對梯度消失
RNN的簡潔實現
import torch
from matplotlib import pyplot as plt
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 定義模型
num_hiddens = 256
rnn_layer = nn.RNN(len(vocab), num_hiddens) # 直接呼叫模型
# 初始化隱狀態
state = torch.zeros((1, batch_size, num_hiddens))
X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state)
# 這裡要注意的是rnn_layer的輸出Y並不是我們想要的預測變數！而是隱狀態！裡面只進行了隱狀態的計算而已
# 完成的RNN模型
#@save
class RNNModel(nn.Module):
"""迴圈神經網路模型"""
def __init__(self, rnn_layer, vocab_size, **kwargs):
super(RNNModel, self).__init__(**kwargs)
self.rnn = rnn_layer # 計算隱狀態
self.vocab_size = vocab_size
self.num_hiddens = self.rnn.hidden_size
# 如果RNN是雙向的（之後將介紹），num_directions應該是2，否則應該是1
if not self.rnn.bidirectional:
self.num_directions = 1
self.linear = nn.Linear(self.num_hiddens, self.vocab_size) # 輸出層計算Y
else:
self.num_directions = 2
self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)
def forward(self, inputs, state):
X = F.one_hot(inputs.T.long(), self.vocab_size)
X = X.to(torch.float32)
Y, state = self.rnn(X, state)
# 全連線層首先將Y的形狀改為(時間步數*批次大小,隱藏單元數)
# 它的輸出形狀是(時間步數*批次大小,詞表大小)。
output = self.linear(Y.reshape((-1, Y.shape[-1])))
return output, state
def begin_state(self, device, batch_size=1):
if not isinstance(self.rnn, nn.LSTM):
# nn.GRU以張量作為隱狀態
return torch.zeros((self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens),device=device)
else:
# nn.LSTM以元組作為隱狀態
return (torch.zeros((
self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device),
torch.zeros((self.num_directions * self.rnn.num_layers,
batch_size, self.num_hiddens), device=device))
# 訓練與預測
device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)
num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)
plt.show()
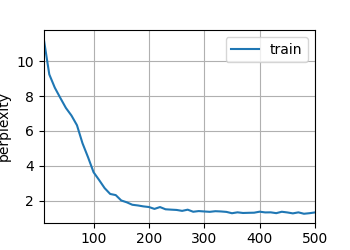
perplexity 1.3, 390784.5 tokens/sec on cuda:0
time travellerit s against reatou dimensions of space generally
traveller pus he iryed it apredinnen it a mamul redoun abs
小結：
- 深度學習框架的高階API提供了RNN層的實現
- 高階API的RNN層返回一個輸出和一個更新後的隱狀態，我們還需要另外一個線型層來計算整個模型的輸出
- 相比從零開始實現的RNN，使用高階API實現可以加速訓練
通過時間反向傳播
在RNN中，前向傳播的計算相對簡單，但是其通過時間反向傳播實際上要求我們將RNN每次對一個時間步進行展開，以獲得模型變數和引數之間的依賴關係，然後基於鏈式法則去應用放反向傳播計算和儲存梯度，這就導致當時間長度T較大時，可能依賴關係會相當長。
假設RNN可表示為：
\[h_t=f(x_t, h_{t-1},w_h)\\
o_t=g(h_t,w_o)\\
損失函數為：L(x_1,..,x_T,y_1,...,y_T,w_h,w_o)=\frac{1}{T}\sum_{t=1}^Tl(y_t,o_t)
\]
那麼在計算梯度時：
\[\frac{\partial L}{\partial w_h}=\frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t,o_t)}{\partial w_h}\\
=\frac{1}{T}\sum_{t=1}^T\frac{\partial l(y_t,o_t)}{\partial o_t}\frac{\partial g(h_t,w_o)}{\partial h_t}\frac{\partial h_t}{\partial w_h}
\]
上述計算中最麻煩的是第三個，因為\(h_t\)不僅依賴於\(w_h\)，還依賴於\(h_{t-1}\)，而\(h_{t-1}\)也依賴於\(w_h\)，這樣就會不停計算下去，即：
\[\frac{\partial h_t}{\partial w_h}=\frac{\partial f(x_t,h_{t-1},w_h)}{\partial w_h}+\sum_{i=1}^{t-1}(\prod_{j=i+1}^t \frac{\partial f(x_j,h_{j-1},w_h)}{\partial h_{j-1}})\frac{\partial f(x_i,h_{i-1},w_h)}{\partial w_h}
\]
那麼如果採用上述完成的鏈式計算，當t很大時這個鏈就會變得很長，難以計算。具體有以下幾種辦法。
完全計算
顯然最簡單的思想當然是直接計算，但是這樣非常緩慢，並且很可能會發生梯度爆炸，因為初始條件的額微小變化就可能因為連乘而帶給結果巨大的影響，就類似於蝴蝶效應，這是不可取的。
截斷時間步
可以在\(\tau\)步後截斷上述的求和運算，即將鏈式法則終止於\(\frac{\partial h_{t-\tau}}{\partial w_h}\)，這樣通常被稱為截斷的通過時間反向傳播。這麼做會導致模型主要側重於短期影響，而不是長期影響，它會將估計值偏向更簡單和更穩定的模型。
隨機截斷
引入一個隨機變數來代替\(\frac{\partial h_t}{\partial w_h}\)，即定義\(P(\xi_t=0)=1-\pi_t,P(\xi_t=\pi_t^{-1})=\pi_t\)，那麼\(E[\xi_t]=1\)，令：
\[z_t=\frac{\partial f(x_t,h_{t-1},w_h)}{\partial w_h}+\xi_t \frac{\partial f(x_t,h_{t-1},w_h)}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial w_h}
\]
那麼可以推匯出\(E[z_t]=\frac{\partial h_t}{\partial w_h}\)，這就導致了不同長度的截斷，
門控迴圈單元GRU
這個機制是引入了重置門和更新門來更好地控制時序資訊的傳遞，具體如下：
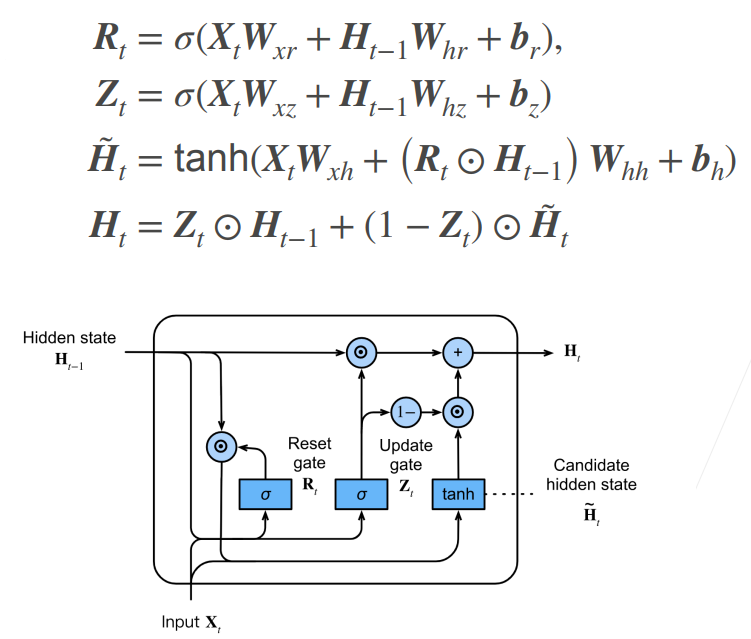
可以看到其中\(R_t、Z_t\)分別稱為重置門和更新門，那麼當\(Z_t=1\)時，\(H_t=H_{t-1}\)，相當於資訊完全不更新直接傳遞過去；而當\(Z_t=0,R_t=0\)時，相當於此時不關注\(H_{t-1}\)的資訊，截斷時序的傳遞，那就相當於初始化了。
注意這裡\(R_t和H_{t-1}\)之間的計算是按照元素相乘。
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 初始化模型引數，這部分和RNN不同
def get_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size # 輸入輸出都是這個長度的向量
def normal(shape):
return torch.randn(size=shape, device=device) * 0.01
def three(): # 用這個函數可以減少重複寫
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xz, W_hz, b_z = three() # 更新門引數
W_xr, W_hr, b_r = three() # 重置門引數
W_xh, W_hh, b_h = three() # 候選隱狀態引數
# 輸出層引數
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
# 初始化隱狀態
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),)
# 定義模型
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params # 獲取引數
H, = state # 隱狀態
outputs = []
for X in inputs:
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z) # 計算更新門，@是矩陣乘法
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h) # 注意這裡R*H是按元素
H = Z * H + (1 - Z) * H_tilda # 這裡也是按元素
Y = H @ W_hq + b_q # 輸出
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,) # 同樣是疊在一起
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
plt.show()
perplexity 1.1, 16015.2 tokens/sec on cuda:0
time traveller for so it will be convenient to speak of himwas e
traveller for so it will be convenient to speak of himwas e
那麼GRU的簡潔實現也很簡單：
num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab)) # 封裝成model的同時會加上線型層
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
plt.show()
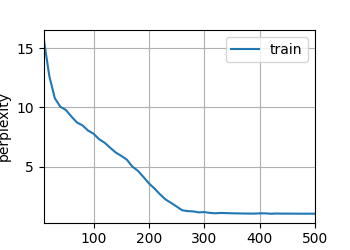
perplexity 1.0, 256679.5 tokens/sec on cuda:0
time traveller for so it will be convenient to speak of himwas e
travelleryou can show black is white by argument said filby
可以看到我們呼叫高階API比從零實現快很多。
小結：
- 門控迴圈神經網路可以更好地捕獲時間步距離很長的序列上的依賴關係
- 重置門有助於捕獲系列中的短期依賴關係
- 更新門有助於捕獲序列中的長期依賴關係
- 重置門開啟時，門控迴圈單元包含基本回圈神經網路；更新門被開啟時，門控迴圈單元可以跳過子序列
長短期記憶網路（LSTM）
這一部分老師講得比較簡單，更關注於實現方面，那麼關於LSTM的比較全面的介紹內容可以觀看李宏毅老師的課程中相關章節，或者閱讀我這篇部落格[點此跳轉]([機器學習]李宏毅——Recurrent Neural Network(迴圈神經網路)_FavoriteStar的部落格-CSDN部落格)。
LSTM的結構具體如下：
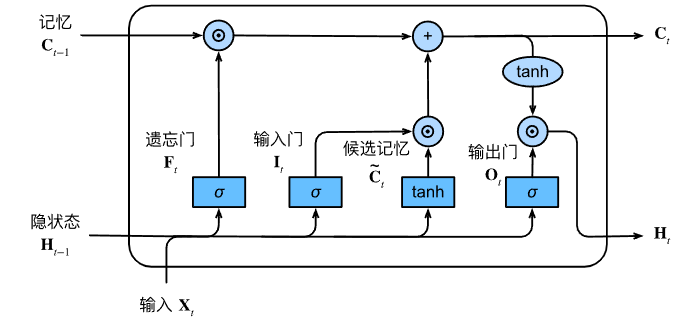
它最主要的特點就是引入了三個門控以及另外一個狀態\(C_t\)來更好地儲存和控制資訊，三個門控分別為：
- 輸入門：決定是否忽略輸入資料
- 忘記門：將數值朝零減少
- 輸出門：決定是否使用隱狀態
\[I_t=\sigma(X_tW_{xi}+H_{t-1}W_{hi}+b_i)\\
F_t=\sigma(X_tW_{xf}+H_{t-1}W_{hf}+b_f)\\
O_t=\sigma(X_tW_{xo}+H_{t-1}W_{ho}+b_o)\\
\tilde{C}_t=\tanh(X_tW_{xc}+H_{t-1}W_{hc}+b_c)\\
C_t=F_t\odot C_{t-1}+I_t\odot \tilde{C}_t\\
H_t=O_t\odot \tanh(C_t)
\]
具體講解可以看我上述提到的那篇部落格。
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 初始化模型引數
def get_lstm_params(vocab_size, num_hiddens, device):
num_inputs = num_outputs = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device)*0.01
def three():
return (normal((num_inputs, num_hiddens)),
normal((num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xi, W_hi, b_i = three() # 輸入門引數
W_xf, W_hf, b_f = three() # 遺忘門引數
W_xo, W_ho, b_o = three() # 輸出門引數
W_xc, W_hc, b_c = three() # 候選記憶元引數
# 輸出層引數
W_hq = normal((num_hiddens, num_outputs))
b_q = torch.zeros(num_outputs, device=device)
# 附加梯度
params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
b_c, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
# 初始化隱狀態，這部分就是兩個了
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
# 定義模型
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
W_hq, b_q] = params # 獲取引數
(H, C) = state # 獲取隱狀態
outputs = []
for X in inputs:
I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
C = F * C + I * C_tilda
H = O * torch.tanh(C)
Y = (H @ W_hq) + b_q # 計算輸出
outputs.append(Y)
return torch.cat(outputs, dim=0), (H, C)
vocab_size, num_hiddens, device = len(vocab), 512, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
init_lstm_state, lstm)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
plt.show()
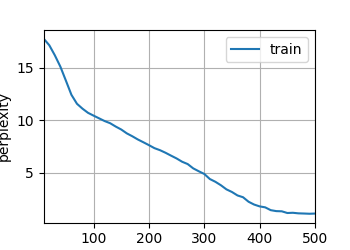
perplexity 1.1, 13369.1 tokens/sec on cuda:0
time traveller well the wild the urais diff me time srivelly are
travelleryou can show black is white by argument said filby
下面是簡潔實現：
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab)) # 同樣會補上輸出的線型層實現
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
plt.show()
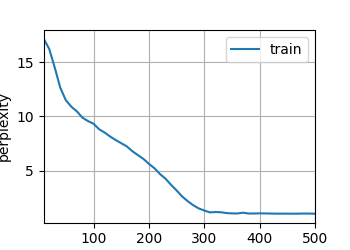
perplexity 1.0, 147043.6 tokens/sec on cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
呼叫高階API的速度是從零實現是十倍往上。
小結：
- LSTM有三種型別的門：輸入門、遺忘門和輸出門
- LSTM隱藏層輸出包括隱狀態和記憶元，只有隱狀態會傳遞到輸出層，而記憶元完全屬於內部資訊
- LSTM可以緩解梯度消失和梯度爆炸的問題，因此多次使用到tanh將輸出對映到[-1,1]之間，具體可以看我那篇部落格最後。
深度迴圈神經網路
為了能夠獲得更多的非線性以及更強的表示能力，我們可以在深度上拓展迴圈神經網路：
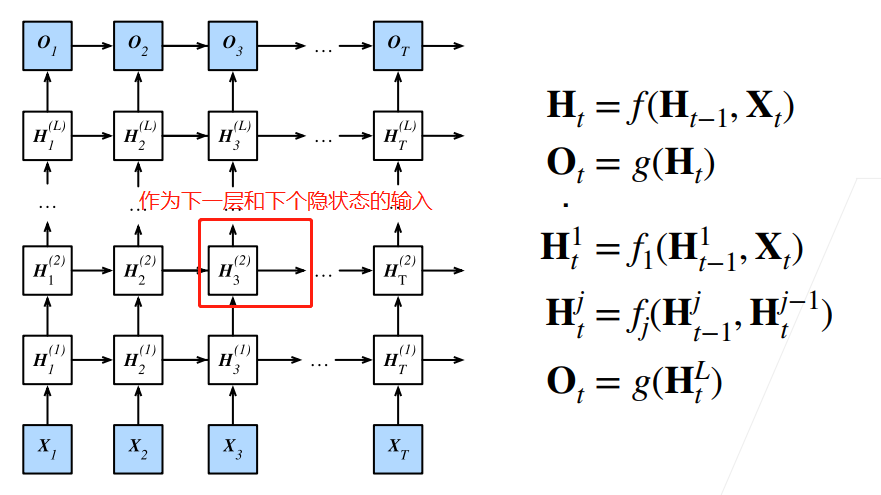
這部分還是很簡單很好理解的，對於GRU和LSTM同樣可以採用。
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2 # 指定隱藏層的層數
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers) # 第三個引數指定隱藏層數目
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
num_epochs, lr = 500, 2
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
plt.show()
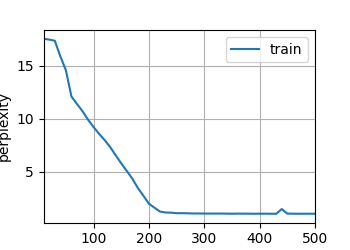
perplexity 1.0, 128068.2 tokens/sec on cuda:0
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby
小結：
- 在深度迴圈神經網路中，隱狀態的資訊被傳遞到當前層的下一時間步和下一層的當前時間步
- 有許多不同風格的深度迴圈神經網路，如LSTM、GRU、RNN等，這些模型都可以用深度學習框架的高階API實現
- 總體而言，深度迴圈神經網路需要大量的調參（如學習率和修剪） 來確保合適的收斂，模型的初始化也需要謹慎。
雙向迴圈神經網路
之前的模型都是觀察歷史的資料來預測未來的資料，但是如果是在一些填空之類的任務中，未來的資訊對這個空也是至關重要的：
因此雙向迴圈神經網路就是可以觀察未來的資訊，它擁有一個前向RNN隱層和一個反向RNN隱層，然後輸出層的輸入是這兩個層隱狀態的合併，如下：
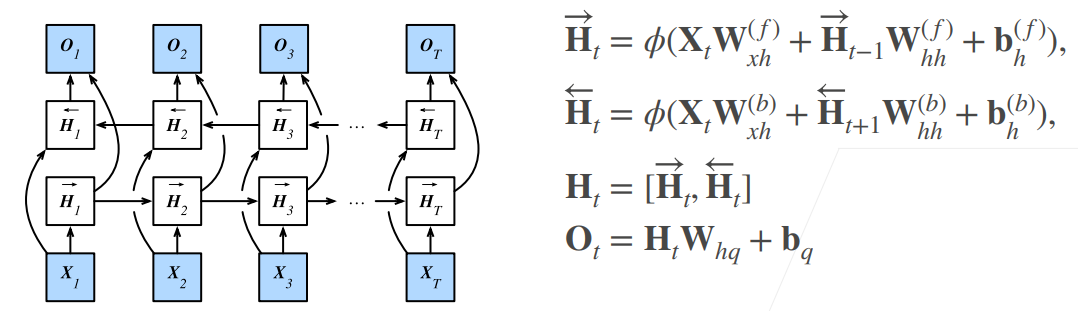
雖然這在訓練的時候是沒問題的，但是這種模型不能用於做預測任務，因此它無法得知未來的資訊，這會造成很糟糕的結果。它最主要的用處是用來對序列進行特徵抽取，因為它能夠觀察到未來的資訊，因此特徵抽取會更加全面。
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
# 載入資料
batch_size, num_steps, device = 32, 35, d2l.try_gpu()
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
# 通過設定「bidirective=True」來定義雙向LSTM模型
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers, bidirectional=True)
model = d2l.RNNModel(lstm_layer, len(vocab)) # 裡面已經設定了當為雙向時線性層會不同
model = model.to(device)
# 訓練模型
num_epochs, lr = 500, 1
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)
plt.show()
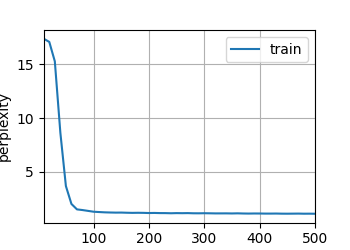
perplexity 1.1, 76187.7 tokens/sec on cuda:0
time travellerererererererererererererererererererererererererer
travellerererererererererererererererererererererererererer
可以看到預測的效果是極差的。
小結：
- 在雙向迴圈神經網路中，每個時間步的隱狀態由當前時間步的前後資料同時決定。
- 雙向迴圈神經網路與概率圖模型中的「前向-後向」演演算法具有相似性。
- 雙向迴圈神經網路主要用於序列編碼和給定雙向上下文的觀測估計。
- 由於梯度鏈更長，因此雙向迴圈神經網路的訓練代價非常高。
機器翻譯與資料集
import os
import torch
from d2l import torch as d2l
#@save
from matplotlib import pyplot as plt
d2l.DATA_HUB['fra-eng'] = (d2l.DATA_URL + 'fra-eng.zip',
'94646ad1522d915e7b0f9296181140edcf86a4f5')
#@save
def read_data_nmt():
"""載入「英語－法語」資料集"""
data_dir = d2l.download_extract('fra-eng')
with open(os.path.join(data_dir, 'fra.txt'), 'r',encoding='utf-8') as f:
return f.read()
raw_text = read_data_nmt()
print(raw_text[:75])
#@save
def preprocess_nmt(text):
"""預處理「英語－法語」資料集"""
def no_space(char, prev_char):
return char in set(',.!?') and prev_char != ' '
# 使用空格替換不間斷空格
# 使用小寫字母替換大寫字母
text = text.replace('\u202f', ' ').replace('\xa0', ' ').lower() # 將utf-8中半形全形空格都換成空格
# 在單詞和標點符號之間插入空格
out = [' ' + char if i > 0 and no_space(char, text[i - 1]) else char
for i, char in enumerate(text)]
return ''.join(out)
text = preprocess_nmt(raw_text)
print(text[:80])
#@save
def tokenize_nmt(text, num_examples=None):
"""詞元化「英語－法語」資料資料集"""
source, target = [], []
for i, line in enumerate(text.split('\n')):
if num_examples and i > num_examples:
break
parts = line.split('\t') # 按照製表符將英文和法文分開
if len(parts) == 2: # 說明前面是英文，後面是法文
source.append(parts[0].split(' ')) # 按照我們前面插入的空格來劃分
target.append(parts[1].split(' '))
return source, target
source, target = tokenize_nmt(text)
print(source[:6], target[:6])
def show_list_len_pair_hist(legend, xlabel, ylabel, xlist, ylist):
"""繪製列表長度對的直方圖"""
d2l.set_figsize()
_, _, patches = d2l.plt.hist(
[[len(l) for l in xlist], [len(l) for l in ylist]])
d2l.plt.xlabel(xlabel)
d2l.plt.ylabel(ylabel)
for patch in patches[1].patches:
patch.set_hatch('/')
d2l.plt.legend(legend)
show_list_len_pair_hist(['source', 'target'], '# tokens per sequence',
'count', source, target)
plt.show()
src_vocab = d2l.Vocab(source, min_freq=2,reserved_tokens=['<pad>', '<bos>', '<eos>'])
# 轉換成詞表，然後加入一些特殊的詞，分別是填充、開始、結尾
print(len(src_vocab))
#@save
def truncate_pad(line, num_steps, padding_token): # 這是為了保證我們的輸入都是等長的
"""截斷或填充文字序列"""
if len(line) > num_steps: # 如果這個句子的長度大於設定長度，我們就截斷
return line[:num_steps] # 截斷
return line + [padding_token] * (num_steps - len(line)) # 如果小於就進行填充
print(truncate_pad(src_vocab[source[0]], 10, src_vocab['<pad>']))
#@save
def build_array_nmt(lines, vocab, num_steps):
"""將機器翻譯的文字序列轉換成小批次"""
lines = [vocab[l] for l in lines] # 將文字轉換為向量
lines = [l + [vocab['<eos>']] for l in lines] # 每一個都要加上結尾符
array = torch.tensor([truncate_pad(l, num_steps, vocab['<pad>']) for l in lines])
# 進行填充或截斷
valid_len = (array != vocab['<pad>']).type(torch.int32).sum(1)
# 這是把每個句子除填充外的有效長度都標註出來，之後計算會用到
return array, valid_len
#@save
def load_data_nmt(batch_size, num_steps, num_examples=600):
"""返回翻譯資料集的迭代器和詞表"""
text = preprocess_nmt(read_data_nmt()) # 預處理
source, target = tokenize_nmt(text, num_examples) # 生成英文和法文兩部分
# 轉成詞典
src_vocab = d2l.Vocab(source, min_freq=2,reserved_tokens=['<pad>', '<bos>', '<eos>'])
tgt_vocab = d2l.Vocab(target, min_freq=2,reserved_tokens=['<pad>', '<bos>', '<eos>'])
src_array, src_valid_len = build_array_nmt(source, src_vocab, num_steps)
tgt_array, tgt_valid_len = build_array_nmt(target, tgt_vocab, num_steps)
data_arrays = (src_array, src_valid_len, tgt_array, tgt_valid_len)
data_iter = d2l.load_array(data_arrays, batch_size) # 一次迭代含有4個變數
return data_iter, src_vocab, tgt_vocab
train_iter, src_vocab, tgt_vocab = load_data_nmt(batch_size=2, num_steps=8)
for X, X_valid_len, Y, Y_valid_len in train_iter:
print('X:', X.type(torch.int32))
print('X的有效長度:', X_valid_len)
print('Y:', Y.type(torch.int32))
print('Y的有效長度:', Y_valid_len)
break
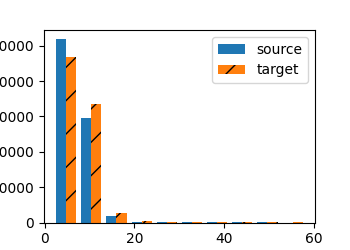
Go. Va !
Hi. Salut !
Run! Cours !
Run! Courez !
Who? Qui ?
Wow! Ça alors !
go . va !
hi . salut !
run ! cours !
run ! courez !
who ? qui ?
wow ! ça alors !
[['go', '.'], ['hi', '.'], ['run', '!'], ['run', '!'], ['who', '?'], ['wow', '!']] [['va', '!'], ['salut', '!'], ['cours', '!'], ['courez', '!'], ['qui', '?'], ['ça', 'alors', '!']]
10012
[47, 4, 1, 1, 1, 1, 1, 1, 1, 1]
X: tensor([[ 7, 0, 4, 3, 1, 1, 1, 1],
[118, 55, 4, 3, 1, 1, 1, 1]], dtype=torch.int32)
X的有效長度: tensor([4, 4])
Y: tensor([[6, 7, 0, 4, 3, 1, 1, 1],
[0, 4, 3, 1, 1, 1, 1, 1]], dtype=torch.int32)
Y的有效長度: tensor([5, 3])
小結：
- 機器翻譯指的是將文字序列從一種語言自動翻譯成另一種語言。
- 使用單詞級詞元化時的詞表大小，將明顯大於使用字元級詞元化時的詞表大小。為了緩解這一問題，我們可以將低頻詞元視為相同的未知詞元。
- 通過截斷和填充文字序列，可以保證所有的文字序列都具有相同的長度，以便以小批次的方式載入。
編碼器-解碼器架構
這是一個很重要的模型。因為機器翻譯是序列轉換模型中的一個核心問題，其輸入和輸出都是長度可變的序列。那麼為了處理這種型別的結構，我們便使用到了編碼器-解碼器架構。
首先是編碼器，它接受一個長度可變的序列作為輸入，然後將其轉換為具有固定形狀的編碼狀態；然後是解碼器，它將固定形狀的編碼狀態對映到長度可變的序列，如下：
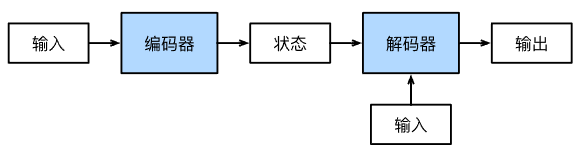
對於AE自編碼器的介紹可以看我這篇部落格，講得比較仔細，有助於理解這種結構。
from torch import nn
#@save
class Encoder(nn.Module):
"""編碼器-解碼器架構的基本編碼器介面"""
def __init__(self, **kwargs):
super(Encoder, self).__init__(**kwargs)
def forward(self, X, *args):
raise NotImplementedError
#@save
class Decoder(nn.Module):
"""編碼器-解碼器架構的基本解碼器介面"""
def __init__(self, **kwargs):
super(Decoder, self).__init__(**kwargs)
def init_state(self, enc_outputs, *args): # 這部分就是編碼後的狀態
raise NotImplementedError
def forward(self, X, state):
raise NotImplementedError
#@save
class EncoderDecoder(nn.Module):
"""編碼器-解碼器架構的基礎類別"""
def __init__(self, encoder, decoder, **kwargs):
super(EncoderDecoder, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X, *args):
enc_outputs = self.encoder(enc_X, *args) # 計算編碼後的值
dec_state = self.decoder.init_state(enc_outputs, *args)
return self.decoder(dec_X, dec_state) # 解碼
小結：
- 編碼器－解碼器架構可以將長度可變的序列作為輸入和輸出，因此適用於機器翻譯等序列轉換問題。
- 編碼器將長度可變的序列作為輸入，並將其轉換為具有固定形狀的編碼狀態。
- 解碼器將具有固定形狀的編碼狀態對映為長度可變的序列。
序列到序列學習（Seq2Seq)
這種任務就是給定一個序列，我們希望將其變換為另一個序列，最典型的應用就是機器翻譯，它給定一個源語言的句子並將其翻譯為目標語言。那麼這就要求給定句子的長度是可變的，而且翻譯後的句子可以有不同的長度。
那麼這個任務最開始用的是編碼器-解碼器架構來做的：
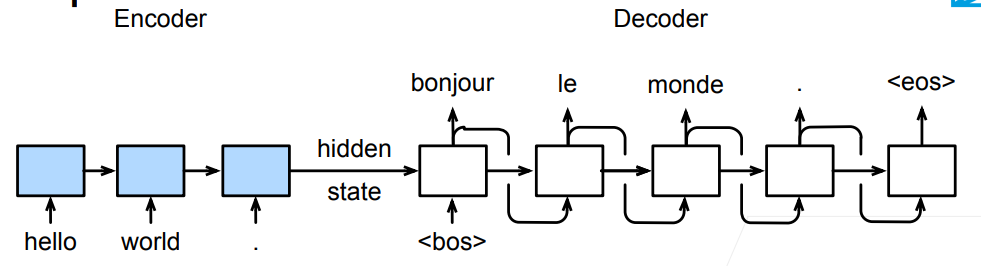
且編碼器和解碼器用的都是RNN的模型。
編碼器中RNN使用長度可變的序列作為輸入，將其轉換為固定形狀的隱狀態，此時輸入序列的資訊都被編碼到隱狀態中；然後將該編碼器的最後一個隱狀態作為解碼器的初始隱狀態，解碼器的RNN根據該初始隱狀態和自己的輸入，開始進行預測。
那麼這種架構在訓練和預測的時候有所不同，在訓練時解碼器的輸入一直都是正確的預測結果，而在預測的時候解碼器的輸入就是本身預測的上一個結果，不一定正確。
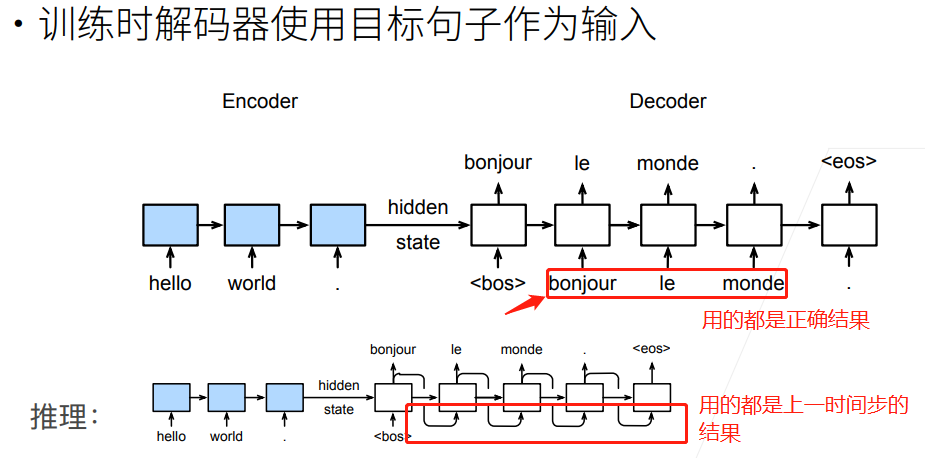
而因為現在我們不僅僅是預測字母，我們是預測整個句子，因此需要一個新的衡量指標來量化預測句子的好壞。常用的是BLEU，其具體如下：
設\(p_n\)是預測中所有n-gram的精度，例如真實序列ABCDEF和預測序列ABBCD，那麼\(p_1\)就是預測序列中單個單元（A,B,B,C,D）在真實序列中是否出現，可以看到總共有4個出現了（B只出現1次）因此\(p_1=\frac{4}{5}\)，同理\(p_2=\frac{3}{4}\)，\(p_3=\frac{1}{3}\)，\(p_4=0\)。
而BLEU的定義如下：
\[ { }
\exp \bigg( \min \Big( 0,~~1-\frac{len_{label}}{len_{pred}} \Big) \bigg)\prod_{n=1}^k p_n^{\frac{1}{2^n}}
\]
其中指數項是為了懲罰過短的預測，因此如果我只預測單個單元，那麼只要其出現了我所有的\(p_n\)(也就是\(p_1\))就是1了，但這是不行的。第二項因為p都是小於1的，因此較長的匹配其指數(\(\frac{1}{2^n}\))會較小，因此可以認為其具有更大的權重。
import collections
import math
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
# @save
class Seq2SeqEncoder(d2l.Encoder):
"""用於序列到序列學習的迴圈神經網路編碼器"""
def __init__(self, vocab_size, embed_size, num_hiddens,
num_layers, dropout=0, **kwargs):
super(Seq2SeqEncoder, self).__init__(**kwargs)
# 嵌入層
self.embedding = nn.Embedding(vocab_size, embed_size)
# 詞嵌入，將文字自動轉換成詞向量
self.rnn = nn.GRU(embed_size, num_hiddens, num_layers, dropout=dropout)
# 因為已經轉換為詞向量，因此輸入為詞向量的長度
def forward(self, X, *args):
# 輸出'X'的形狀：(batch_size,num_steps,embed_size)
X = self.embedding(X) # 先轉換為詞向量
# 在迴圈神經網路模型中，第一個軸對應於時間步
X = X.permute(1, 0, 2) # 轉換為時間步*批次大小*長度
# 如果未提及狀態，則預設為0
output, state = self.rnn(X)
# output的形狀:(num_steps,batch_size,num_hiddens)，
# 因為有多層，它可以認為是最後一層的所有時間步的隱狀態輸出
# state的形狀:(num_layers,batch_size,num_hiddens)
# 它是所有層的最後一個時間步的隱狀態輸出
return output, state
class Seq2SeqDecoder(d2l.Decoder):
"""用於序列到序列學習的迴圈神經網路解碼器"""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqDecoder, self).__init__(**kwargs)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,
dropout=dropout)
# 因為下面做了拼接處理，因此這裡輸入的維度為embed_size+num_hiddens
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, *args):
return enc_outputs[1] # 裡面有output,state，【1】就是把state拿出來
def forward(self, X, state):
# 輸出'X'的形狀：(batch_size,num_steps,embed_size)
X = self.embedding(X).permute(1, 0, 2)
# 廣播context，使其具有與X相同的num_steps state[-1]是前面最後一層的最後一個隱狀態
context = state[-1].repeat(X.shape[0], 1, 1)
# context的維度為num_steps，1，num_hiddens
X_and_context = torch.cat((X, context), 2)
# 將它們拼在一起，即輸入embed_size+num_hiddens
# 這裡可以認為是：我覺得單純的隱狀態的傳遞不夠，我再將最後一層的最後一個隱狀態
# 和我的第一個輸入拼在一起，我覺得它濃縮了很多資訊，也一起來作為輸入
output, state = self.rnn(X_and_context, state)
output = self.dense(output).permute(1, 0, 2)
# output的形狀:(batch_size,num_steps,vocab_size)
# state的形狀:(num_layers,batch_size,num_hiddens)
return output, state
# @save
def sequence_mask(X, valid_len, value=0): # 該函數生成mask並進行遮擋
"""在序列中遮蔽不相關的項"""
maxlen = X.size(1) # 取出X中的第一維度的數量
mask = torch.arange((maxlen), dtype=torch.float32,
device=X.device)[None, :] < valid_len[:, None]
# arange生成一個一維的tensor，[None,:]是將其變成二維的，1*maxlen的tensor
# 而valid_len是長度為max_len的向量，[:,None]就變成了max_len*1的tensor
# 然後小於就會觸發廣播機制，例如max_len=4,那麼arange生成的[[1,2,3,4]]就會廣播
# 變成4行，每一行都是[1,2,3,4]，那麼將每一列和valid_len這個列比較
# 因為valid_len中的元素就是多少個有效的，那麼假設2，就是前兩個為true，後兩個為false
# 這樣就可以將其提取出來了
X[~mask] = value
return X
# @save
class MaskedSoftmaxCELoss(nn.CrossEntropyLoss):
"""帶遮蔽的softmax交叉熵損失函數"""
# pred的形狀：(batch_size,num_steps,vocab_size)
# label的形狀：(batch_size,num_steps)
# valid_len的形狀：(batch_size,)
def forward(self, pred, label, valid_len):
weights = torch.ones_like(label)
weights = sequence_mask(weights, valid_len)
self.reduction = 'none' # 不對求出來的損失求和、平均等操作
unweighted_loss = super(MaskedSoftmaxCELoss, self).forward(
pred.permute(0, 2, 1), label) # 這裡維度轉換為torch本身的要求
weighted_loss = (unweighted_loss * weights).mean(dim=1) # 按元素相乘
return weighted_loss
# @save
def train_seq2seq(net, data_iter, lr, num_epochs, tgt_vocab, device):
"""訓練序列到序列模型"""
def xavier_init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
if type(m) == nn.GRU:
for param in m._flat_weights_names:
if "weight" in param:
nn.init.xavier_uniform_(m._parameters[param])
net.apply(xavier_init_weights)
net.to(device)
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
loss = MaskedSoftmaxCELoss()
net.train() # 開啟訓練模式
animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[10, num_epochs])
for epoch in range(num_epochs):
timer = d2l.Timer()
metric = d2l.Accumulator(2) # 訓練損失總和，詞元數量
for batch in data_iter:
optimizer.zero_grad() # 清空梯度
X, X_valid_len, Y, Y_valid_len = [x.to(device) for x in batch]
# 英文、英文有效長度、法文、法文有效長度
bos = torch.tensor([tgt_vocab['<bos>']] * Y.shape[0], device=device).reshape(-1, 1) # 轉換為相同緯度
# Y是法文，在訓練時是作為解碼器的輸入的，然後我們需要一個開始標註
# 因此我們將Y的最後一個單詞去掉，再在第一個前面加上一個開始標誌bos
# 這樣我們強制讓它學習bos去預測第一個詞，而最後一個詞它不會用來做預測，因此在預測時它去掉沒關係
# 那之後在真正預測的時候，我們就只需要給解碼器第一個為bos，後面它自己生成的拿來做輸入就可以
dec_input = torch.cat([bos, Y[:, :-1]], 1) # 強制教學
Y_hat, _ = net(X, dec_input, X_valid_len) # 這個模型的第一個引數的編碼器輸入，第二個是解碼器輸入
# 第三個是編碼器輸入的有效長度
l = loss(Y_hat, Y, Y_valid_len) # 這裡就是用原來的Y去和預測的做損失
l.sum().backward() # 損失函數的標量進行「反向傳播」
d2l.grad_clipping(net, 1) # 梯度裁剪
num_tokens = Y_valid_len.sum()
optimizer.step()
with torch.no_grad():
metric.add(l.sum(), num_tokens)
if (epoch + 1) % 10 == 0:
animator.add(epoch + 1, (metric[0] / metric[1],))
print(f'loss {metric[0] / metric[1]:.3f}, {metric[1] / timer.stop():.1f} '
f'tokens/sec on {str(device)}')
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10 # 10是句子最長為10，超過裁剪，不足就補充
lr, num_epochs, device = 0.005, 300, d2l.try_gpu()
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = Seq2SeqEncoder(len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqDecoder(len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
plt.show()
# @save
def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps, device,
save_attention_weights=False):
"""序列到序列模型的預測"""
# 在預測時將net設定為評估模式
net.eval()
# 將輸入的句子變成小寫再按空格分隔再加上結尾符,並且都經過src_vocab這個類轉換成向量了
src_tokens = src_vocab[src_sentence.lower().split(' ')] + [src_vocab['<eos>']]
# 該句子的有效長度
enc_valid_len = torch.tensor([len(src_tokens)], device=device)
# 對該句子檢查長度進行填充或者裁剪
src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
# 新增批次軸，將src_tokens新增上批次這個維度，因此變成批次*時間步*vocabsize
enc_X = torch.unsqueeze(torch.tensor(src_tokens, dtype=torch.long, device=device),
dim=0)
# 計算encoder的輸出
enc_outputs = net.encoder(enc_X, enc_valid_len)
# 計算decoder應該接受的初始狀態
dec_state = net.decoder.init_state(enc_outputs, enc_valid_len)
# 新增批次軸,因為現在是預測因此decoer的輸入只有一個<bos>，那麼為它新增一個批次軸
dec_X = torch.unsqueeze(torch.tensor(
[tgt_vocab['<bos>']], dtype=torch.long, device=device), dim=0) # 增加一個維度
output_seq, attention_weight_seq = [], []
for _ in range(num_steps):
Y, dec_state = net.decoder(dec_X, dec_state) # 輸出和隱狀態
# 我們使用具有預測最高可能性的詞元，作為解碼器在下一時間步的輸入
dec_X = Y.argmax(dim=2) # 更新輸入
pred = dec_X.squeeze(dim=0).type(torch.int32).item() # 去除批次這個維度
# 儲存注意力權重（稍後討論）
if save_attention_weights:
attention_weight_seq.append(net.decoder.attention_weights)
# 一旦序列結束詞元被預測，輸出序列的生成就完成了
if pred == tgt_vocab['<eos>']:
break
output_seq.append(pred)
return ' '.join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq
def bleu(pred_seq, label_seq, k): #@save
"""計算BLEU"""
pred_tokens, label_tokens = pred_seq.split(' '), label_seq.split(' ')
len_pred, len_label = len(pred_tokens), len(label_tokens)
score = math.exp(min(0, 1 - len_label / len_pred))
for n in range(1, k + 1):
num_matches, label_subs = 0, collections.defaultdict(int)
for i in range(len_label - n + 1):
# 這個迴圈是將真實序列中的各種長度的連續詞彙都變成詞典計數
label_subs[' '.join(label_tokens[i: i + n])] += 1
for i in range(len_pred - n + 1):
if label_subs[' '.join(pred_tokens[i: i + n])] > 0:
num_matches += 1 # 這裡判斷出來預測序列中有對應的n-gram
label_subs[' '.join(pred_tokens[i: i + n])] -= 1 # 要減一
score *= math.pow(num_matches / (len_pred - n + 1), math.pow(0.5, n))
return score
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, attention_weight_seq = predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device)
print(f'{eng} => {translation}, bleu {bleu(translation, fra, k=2):.3f}')
loss 0.019, 12068.0 tokens/sec on cuda:0
go . => va !, bleu 1.000
i lost . => j'ai perdu ., bleu 1.000
he's calm . => il est riche ., bleu 0.658
i'm home . => je suis chez moi chez moi chez moi juste ., bleu 0.537
小結：
- 根據「編碼器-解碼器」架構的設計， 我們可以使用兩個迴圈神經網路來設計一個序列到序列學習的模型。
- 在實現編碼器和解碼器時，我們可以使用多層迴圈神經網路。
- 我們可以使用遮蔽來過濾不相關的計算，例如在計算損失時。
- 在「編碼器－解碼器」訓練中，強制教學方法將原始輸出序列（而非預測結果）輸入解碼器。
- BLEU是一種常用的評估方法，它通過測量預測序列和標籤序列之間的n元語法的匹配度來評估預測。
束搜尋
在前面的預測之中，我們採用的策略是貪心策略，也就是每一次預測的時候都是選擇當前概率最大的來作為結果。那麼貪心策略的最終結果通常不是最優的，然後窮舉搜尋計算複雜度太大了，因此有另一種方法為束搜尋來進行改進。
束搜尋有一種關鍵的引數為束寬\(k\)。在時間步1，也就是根據<bos>做第一次預測時，我們不止是選取概率最大的那個來進行輸出，而是選擇具有最高概率的\(k\)個詞元，例如下圖中我們在第一個時間步選擇到了A和C。那麼在之後的時間步中，就會基於上一個時間步所選擇的\(k\)個候選序列，來從\(k\vert Y\vert\)個可能中挑選出具有最高條件概率的\(k\)個候選輸出序列：
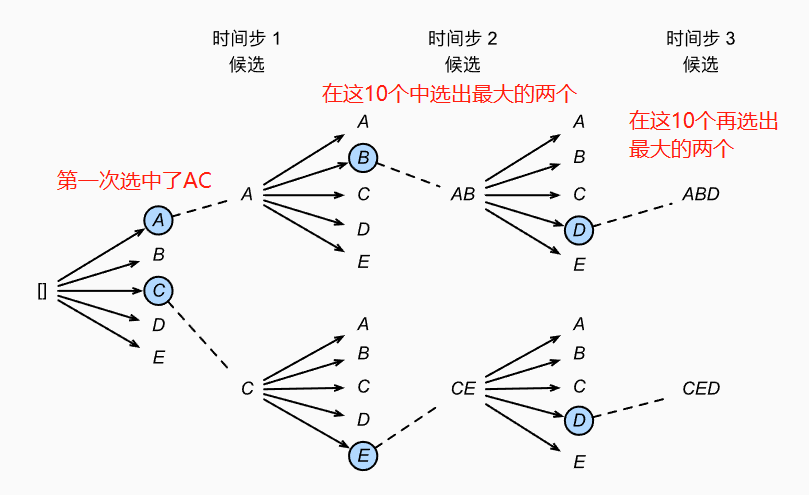
並且，我們不止是考慮最終得到的長序列，而是考慮在選擇過程中選擇到的各個序列，即A,C,AB,CE,ABD,CED這兩個序列。對它們的評估我們採用以下公式進行計算：
\[\frac{1}{L^{\alpha}}\log P(y_1,...,y_L)=\frac{1}{L^{\alpha}}\sum_{t^{\prime}=1}^L \log P(y_{t^{\prime}}\mid y_1,...,y_{t^{\prime}-1})
\]
其中L為序列的長度，\(\alpha\)常取0.75，這部分是為了中和長短序列的差距，因為短序列乘的概率少總是會大一點，因此用這部分來進行中和，相當於給選擇短序列加入了一定的懲罰。
束搜尋的時間複雜度為\(O(k\vert Y\vert T)\)
小結：
- 序列搜尋策略包括貪心搜尋、窮舉搜尋和束搜尋。
- 貪心搜尋所選取序列的計算量最小，但精度相對較低。
- 窮舉搜尋所選取序列的精度最高，但計算量最大。
- 束搜尋通過靈活選擇束寬，在正確率和計算代價之間進行權衡。
注意力機制
注意力機制與注意力分數
第一節課注意力機制的時候我聽完老師的講解一直沒能理解，什麼是注意力機制，但我聽了第二節的注意力分數後才感覺到豁然開朗，因此我就按照自己的方式來進行記錄。
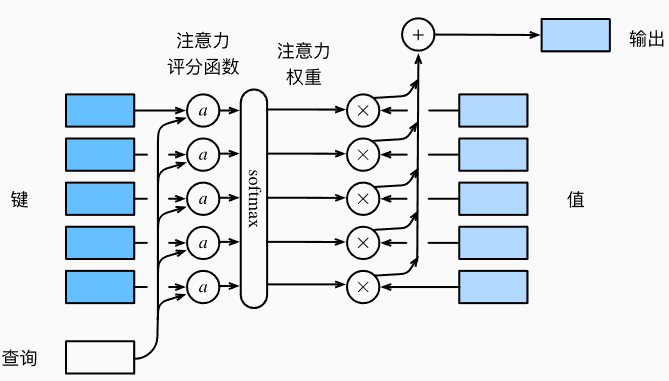
注意力機制完全可以用上圖很好地表示，其中需要注意的幾個點為：
- 鍵：可以認為是已有的樣本\(x_i\)
- 值：可以認為是每個樣本對應的函數值\(y_i=f(x_i)\)
- 查詢：可以認為是我們新得到的輸入\(\hat{x}\)
而我們的目的是希望能夠通過鍵和值來計算未知的\(f(\hat{x})\)
那麼注意力機制的方法就是通過注意力評分函數來計算\(\hat{x}\)與每一個已知樣本\(x_i\)之間的得分，再轉換成權重，再對每一個\(y_i\)進行加權和即可。
那麼對於最簡單的情形，當然是權重都一致，因此相當於取平均：
\[f(\hat{x})=\frac{1}{n}\sum_{i=1}^ny_i
\]
而這樣的效果通常是較差的，因此通常是根據各種方式來計算評分與權重：
\[f(\hat{x})=\sum_{i=1}^n \alpha(\hat{x},x_i)y_i=\sum_{i=1}^nsoftmax(a(\hat{x},x_i))y_i
\]
即用函數a計算評分，再經過softmax轉換為權重\(\alpha\)。
對於標量來說，比較直觀的思想當然是計算兩個標量之間的距離，即：
\[a(\hat{x},x_i)=-\frac{1}{2}(\hat{x}-x_i)^2
\]
而拓展到向量的情況，假設查詢為\(\pmb{q}\in R^q\)，具有m個鍵值對\((\pmb{k}_1,\pmb{v}_1),...,(\pmb{k}_m,\pmb{v}_m)\)，其中\(\pmb{k}_i\in R^k,\pmb{v}_i\in R^v\)，注意力匯聚則可寫成：
\[f(\pmb{q})=\sum_{i=1}^m\alpha(\pmb{q},\pmb{k}_i)\pmb{v}_i \in R^v
\]
因此現在就需要對查詢與鍵之間的評分進行衡量，此處介紹兩種方法。
1、Additive Attention
其需要進行引數的學習，可學習的引數為：\(\pmb{W}_k\in R^{h\times k},\pmb{W}_q\in R^{h\times q},\pmb{v}\in R^h\)
\[a(\pmb{k},\pmb{q})=\pmb{v}^T\tanh (\pmb{W}_k\pmb{k}+\pmb{W}_q\pmb{q})
\]
等價於將查詢和鍵進行拼接，成為長度為\((q+k)\)的向量，再經過一個隱藏大小為\(h\)、輸出大小為1的單隱藏層MLP。那麼這種方法就不要求查詢和鍵的長度是一樣的，是很適用的方法。
2、Scaled Dot-Product Attention
這部分不需要進行引數的學習，但它要求查詢和鍵向量長度是相同的，設長度為d，那麼：
\[a(\pmb{q},\pmb{k}_i)=\frac{<\pmb{q},\pmb{k}_i>}{\sqrt{d}}
\]
這裡將兩個向量做內積，然後除以\(\sqrt{d}\)，這是因為長度較長的向量內積會比較大，那麼這部分可以消除長度的影響。
上述演演算法的批次化版本為：
\[\pmb{Q}\in R^{n\times d},\pmb{K}\in R^{m\times d},\pmb{V}\in R^{m\times v}\\
注意力分數：a(\pmb{Q},\pmb{K})=\frac{\pmb{Q}\pmb{K}^T}{\sqrt{d}}\in R^{n\times m}\\
注意力匯聚：f=softmax\big(a(\pmb{Q},\pmb{K}) \big)\pmb{K}\in R^{n\times v}
\]
import math
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
# 先定義遮擋的softmax操作，因為我們有時候並不是要利用所有的鍵值對
def masked_softmax(X, vaild_lens):
if vaild_lens is None:
return nn.functional.softmax(X, dim=-1)
# 如果不進行遮擋，那麼就直接進行softmax就好
else:
shape = X.shape # X的維度是（批次數，批次內樣本數目，樣本長度）
if vaild_lens.dim() == 1: # 說明是一個向量，不是矩陣
vaild_lens = torch.repeat_interleave(vaild_lens, shape[1])
# 例如vaild_lens[1,2],內部元素的意義是對於兩個批次
# 第一個批次內所有樣本只需要看第一個鍵值對，第二個批次內所有樣本只看前兩個鍵值對
# 而在批次內樣本數目的維度進行復制，例如樣本數目為3，那麼就會變成
# [1,1,1,2,2,2]，這樣就是針對每一個樣本的有效長度了
else:
vaild_lens = vaild_lens.reshape(-1)
# 因為已經是矩陣了，就已經是我們針對每一個樣本的有效長度了
# 例如上面的[1,1,1,2,2,2]只不過維度是[[1,1,1],[2,2,2]]
# 那麼我們將其展開成一維的[1,1,1,2,2,2]就可以了
X = d2l.sequence_mask(X.reshape(-1, shape[-1]), vaild_lens, value=-1e6)
# 將X展開，然後那些無效的就設成負數使其指數接近於0
return nn.functional.softmax(X.reshape(shape), dim=-1)
# 加性注意力實現
# @save
class AdditiveAttention(nn.Module):
def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
self.w_v = nn.Linear(num_hiddens, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
# 兩者先經過線性模型的處理
# 此時queries形狀為（批次數目，單個批次的查詢個數，num_hidden）
# keys形狀為（批次數目，單個批次的鍵個數，num_hidden）
# 這樣是不能直接相加的，我們的目的是每一個q都跟每個k加一次
# 因此拓展維度
# 在維度擴充套件後，
# queries的形狀：(batch_size，查詢的個數，1，num_hidden)
# key的形狀：(batch_size，1，「鍵－值」對的個數，num_hiddens)
# 使用廣播方式進行求和，我們想要讓每個查詢，都和每個key加一次，
# 因此出來時(batch_size,查詢個數，鍵個數，num_hidden)
features = queries.unsqueeze(2) + keys.unsqueeze(1)
features = torch.tanh(features)
scores = self.w_v(features).squeeze(-1) # 最後一個維度是1，因為是標量
# 去掉最後一個維度就變成(batch_size,查詢個數，鍵個數)
self.attention_weights = masked_softmax(scores, valid_lens)
# 獲取權重，其中將無效的轉換為0了
return torch.bmm(self.dropout(self.attention_weights), values)
# 進行dropout丟棄掉其中一部分權重，但dropout是保證加起來為1的，然後再最進行遮擋的相乘bmm
# 實現縮放點積注意力
class DotProductAttention(nn.Module):
def __init__(self, dropout, **kwargs):
super(DotProductAttention, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens=None):
# queries的形狀：(batch_size，查詢的個數，d)
# keys的形狀：(batch_size，「鍵－值」對的個數，d)
# values的形狀：(batch_size，「鍵－值」對的個數，值的維度)
# valid_lens的形狀:(batch_size，)或者(batch_size，查詢的個數)
d = queries.shape[-1]
scores = torch.bmm(queries, keys.transpose(1,2))/math.sqrt(d)
# 將k最後面的兩個維度進行交換，也就相當於轉置了,然後用batch方式的相乘
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
if __name__ == "__main__":
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批次，兩個值矩陣是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(
2, 1, 1)
valid_lens = torch.tensor([2, 6])
attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
dropout=0.1)
attention.eval()
print(attention(queries, keys, values, valid_lens))
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')
plt.show()
queries = torch.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.eval()
print(attention(queries, keys, values, valid_lens))
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')
plt.show()
tensor([[[ 2.0000, 3.0000, 4.0000, 5.0000]],
[[10.0000, 11.0000, 12.0000, 13.0000]]], grad_fn=<BmmBackward0>)
tensor([[[ 2.0000, 3.0000, 4.0000, 5.0000]],
[[10.0000, 11.0000, 12.0000, 13.0000]]])
小結：
- 注意力分數是查詢和鍵的相似度，注意力權重是分數的softmax結果
- 兩種常見的分數計算為：
- 將查詢和鍵合併起來進入一個單輸出單隱藏層的MLP
- 直接將查詢和鍵做內積
自注意力機制用於Seq2Seq
例如前面英文翻譯成法文的句子，在Decoder中，我們是將Encoder的最後時間步的最後隱藏層的輸出的隱狀態，來和輸入拼接，再輸入到Decoder中。但這就存在問題就是例如hello world進行翻譯，第一個翻譯出來的法語應該是和hello這個單詞對應的隱狀態輸出息息相關的，然後後面的法語應該是和world對應的息息相關的，如下圖：
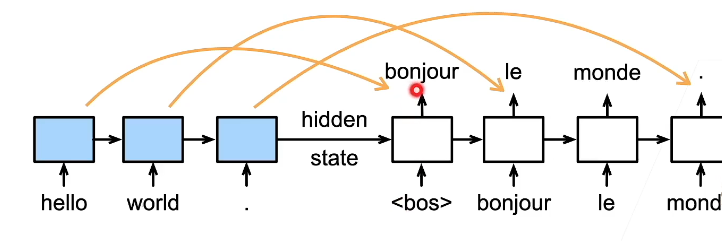
但是我們的機制並不能夠注意到這一點，而是直接將濃縮到最後的隱狀態拿來使用。
那麼我們引入注意力機制來實現這個目的，具體的做法就是：
- 將原先我們用於和輸入進行拼接的隱狀態作為查詢\(q\)，將Encoder的最後一層的所有時間步的隱狀態輸出作為鍵值\(k、v\)(注意兩者是一模一樣的)
- 然後用\(q、k、v\)輸入到注意力機制當中，也就是說將本來的q，去Encoder中變換成和它比較接近的，有接近意義的v。
- 然後再將新得到的隱狀態和輸入拼接進行輸入
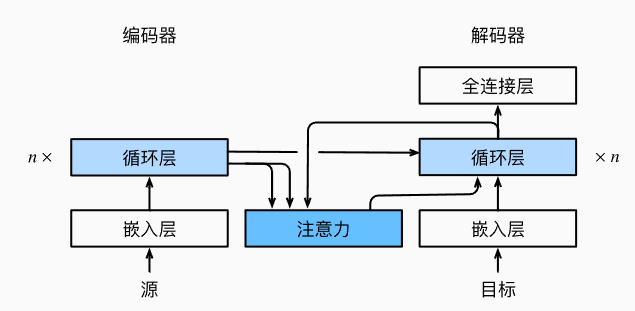
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
# 定義帶有注意力機制解碼器的基本介面，這部分我也不太理解其意義所在
#@save
class AttentionDecoder(d2l.Decoder):
"""帶有注意力機制解碼器的基本介面"""
def __init__(self, **kwargs):
super(AttentionDecoder, self).__init__(**kwargs)
@property
def attention_weights(self):
raise NotImplementedError
# 實現帶有注意力機制的迴圈神經網路解碼器，因為編碼器和之前是一模一樣的
class Seq2SeqAttentionDecoder(AttentionDecoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqAttentionDecoder,self).__init__(**kwargs)
self.attention = d2l.AdditiveAttention(num_hiddens,num_hiddens, num_hiddens,
dropout)
# 這裡注意力機制的q,k,v，三者都是同樣的形狀，q就可以認為是當前解碼器時間步的輸入
# 而k和v就固定為編碼器所有時間步的最後一層隱藏層的輸出，k和v是一樣的東西，q,v,k三者是相同空間
# 因為我是根據q去查詢，編碼器輸出空間的隱狀態，根據相似程度，輸出最終也需要是q這種形狀的
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size+num_hiddens, num_hiddens, num_layers, dropout=dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
outputs, hidden_state = enc_outputs
# outputs是所有時間步的最後一層的隱狀態輸出
# hidden_state是最後一個時間步的所有層的隱狀態輸出
return (outputs.permute(1,0,2), hidden_state, enc_valid_lens)
def forward(self, X, state):
enc_outputs, hidden_state, enc_valid_lens = state
# 第一個形狀為（批次數，時間步， num_hiddens）
# 第二個形狀為（隱層數，批次數，num_hiddens）
X = self.embedding(X).permute(1,0,2)
outputs, self._attention_weights = [],[]
for x in X:
query = torch.unsqueeze(hidden_state[-1], dim=1)
# 第一次就是取出最後一層的最後一個時間步的隱狀態，然後加入一個維度(batch_size,1,num_hiddens)
# 第二次就是更新得到的隱狀態去查詢了
context = self.attention(query, enc_outputs, enc_outputs, enc_valid_lens)
# 這步就是用這個隱狀態去編碼器的所有隱狀態輸出中查詢，然後轉換計算分數、權重等
# value還是隱狀態，因為我們希望得到的還是一個隱狀態的輸出
x = torch.cat((context, torch.unsqueeze(x,dim=1)), dim=-1)
# 將得到的新的隱狀態和輸入拼接在一起
out, hidden_state = self.rnn(x.permute(1,0,2), hidden_state)
# 這一步就計算輸出並更新隱狀態
outputs.append(out)
self._attention_weights.append(self.attention.attention_weights)
# 此時outputs形狀為batch_size, num_steps, num_hiddens
outputs = self.dense(torch.cat(outputs, dim=0))
# 此時outputs形狀為num_steps, batch_size, vocab_size
return outputs.permute(1,0,2),[enc_outputs, hidden_state, enc_valid_lens]
@property
def attention_weights(self):
return self._attention_weights
if __name__ == "__main__":
encoder = d2l.Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16,
num_layers=2)
encoder.eval()
decoder = Seq2SeqAttentionDecoder(vocab_size=10, embed_size=8, num_hiddens=16,
num_layers=2)
decoder.eval()
X = torch.zeros((4, 7), dtype=torch.long) # (batch_size,num_steps)
state = decoder.init_state(encoder(X), None)
output, state = decoder(X, state)
print("output.shape=\t",output.shape)
print("len(state)=\t",len(state))
print("state[0].shape=\t",state[0].shape)
print("len(state[1]), state[1][0].shape = \t",len(state[1]), state[1][0].shape)
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 250, d2l.try_gpu()
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = d2l.Seq2SeqEncoder(
len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(
len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
plt.show()
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, dec_attention_weight_seq = d2l.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
print(f'{eng} => {translation}, ',
f'bleu {d2l.bleu(translation, fra, k=2):.3f}')
attention_weights = torch.cat([step[0][0][0] for step in dec_attention_weight_seq], 0).reshape((
1, 1, -1, num_steps))
# 加上一個包含序列結束詞元
d2l.show_heatmaps(
attention_weights[:, :, :, :len(engs[-1].split()) + 1].cpu(),
xlabel='Key positions', ylabel='Query positions')
plt.show()
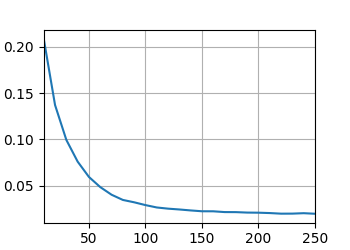
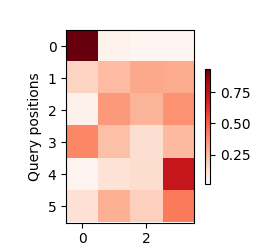
output.shape= torch.Size([4, 7, 10])
len(state)= 3
state[0].shape= torch.Size([4, 7, 16])
len(state[1]), state[1][0].shape = 2 torch.Size([4, 16])
loss 0.020, 4975.5 tokens/sec on cuda:0
go . => va !, bleu 1.000
i lost . => j'ai perdu ., bleu 1.000
he's calm . => il est suis ., bleu 0.658
i'm home . => je suis chez moi ., bleu 1.000
可見效果有所提升。
小結：
- 在預測詞元時，如果不是所有輸入詞元都是相關的，那麼具有Bahdanau注意力的迴圈神經網路編碼器-解碼器會有選擇地統計輸入序列的不同部分。這是通過將上下文變數視為加性注意力池化的輸出來實現的。
- 在迴圈神經網路編碼器-解碼器中，Bahdanau注意力將上一時間步的解碼器隱狀態視為查詢，在所有時間步的編碼器隱狀態同時視為鍵和值。
自注意力與位置編碼
首先關注什麼是自注意力機制
自注意力機制指的是：給定一個序列\(x_1,...,x_n(x_i\in R^d)\)，那麼自注意力池化層將\(x_i\)當成key、value、query來對序列抽取特徵得到\(y_1,...,y_n\)，即：
\[y_i=f(x_i,(x_1,x_1),...,(x_n,x_n))\in R^d
\]
也就是它不需要像前述的Encoder和Decoder結構，只需要輸入序列即可。
那麼比較一下能夠提取序列資訊的幾種結果：CNN、RNN、自注意力
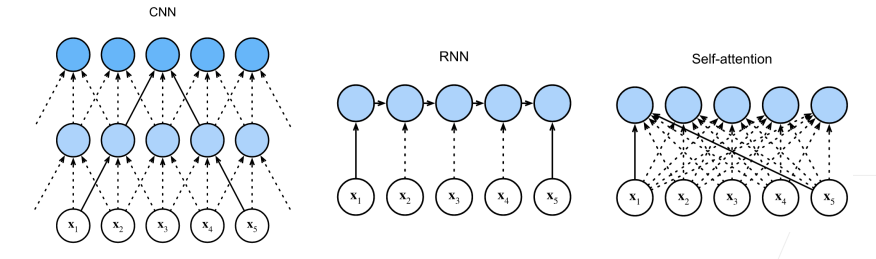
| CNN | RNN | 自注意力 | |
|---|---|---|---|
| 計算複雜度 | O(knd^2) | O(nd^2) | O(n^2d) |
| 並行度 | O(n) | O(1) | O(n) |
| 最長路徑 | O(n/k) | O(n) | O(1) |
可以看到因為自注意力機制是每個輸入\(x_i\)都要和全部序列進行計算，因此它的時間複雜度是\(n^2\)級別的，因此是相當高的，但是因為它的計算沒有像RNN一樣的先後順序，因此其並行度同樣也比較高。而最長路徑指的是序列的第一個樣本要經過多少次計算才能夠將資訊與最後一個樣本結果，那麼因為自注意力一開始就全部進行了計算，因此其最長路徑為1。
而有一個非常重要的特徵，就是自注意力其實並沒有記錄位置資訊，因為假設把輸入序列中的幾個樣本調換位置，那麼它們所產生的輸出也只是調換了位置而已，內容並不會發生變化，因此需要將位置的資訊加入到其中。
而為了保持自注意力機制的長序列讀取能力、並行能力，決定用位置編碼將位置資訊注入到輸入中，即假設長度為n的序列\(\pmb{X}\in R^{n\times d}\)，位置編碼矩陣為\(\pmb{P}\in R^{n\times d}\)，將\(\pmb{X+P}\)作為自注意力機制的輸入。因此我們只需要選擇如何計算位置編碼矩陣即可，通常其計算為：
\[p_{i,2j}=\sin(\frac{i}{10000^{\frac{2j}{d}}}),p_{i,2j+1}=\cos(\frac{i}{10000^{\frac{2j}{d}}})
\]
使用這種編碼存在的好處為位於\(i+\delta\)處的位置編碼可以線性投影到位置\(i\)處的位置編碼，它們之間存在關係可以相關表示為：
\[\left[
\begin{matrix}
\cos(\delta w_j)\quad \sin(\delta w_j)\\
-\sin(\delta w_j)\quad \cos(\delta w_j)
\end{matrix}
\right]
\left[
\begin{matrix}
p_{i,2j}\\
p_{i,2j+1}
\end{matrix}
\right]
=
\left[
\begin{matrix}
p_{i+\delta,2j}\\
p_{i+\delta,2j+1}
\end{matrix}
\right]\\
w_j=\frac{1}{10000^{\frac{2j}{d}}}
\]
即假設兩個樣本想個\(\delta\)，那麼不管它們在序列中的什麼位置，只要保持住相隔的大小，那麼它們之間的相互資訊可以認為是不變的。
多頭注意力
在實際中，我們希望當給定相同的查詢、鍵和值的集合時，模型可以基於同樣的注意力機制學習到不同的行為或特徵，再將這些不同的行為特徵當成知識組合起來，捕獲序列中各種範圍的依賴關係（例如同時捕獲到長距離依賴和短距離依賴）。那麼要實現這個效果，就需要注意力機制組合使用查詢、鍵和值的不同子空間表示來進行學習。
那麼具體的實現方法是用獨立學習得到的h組不同的線性投影來對查詢、鍵和值進行變化(用全連線層對映到較低的維度)，再將h組變換後的查詢、鍵和值並行地送入到注意力匯聚之中，最後將這h個注意局匯聚得到的輸出進行拼接，再經過另外一個可學習的線性投影進行變換，產生最終輸出，這種結構稱為多頭注意力。如下圖：
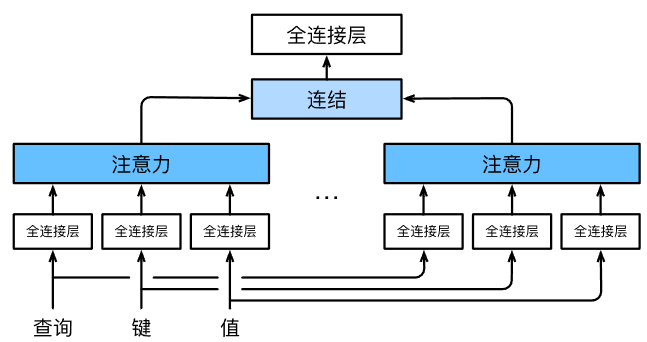
那麼其數學語言為：
給定\(q\in R^{d_q}、k\in R^{d_k}、v\in R^{d_v}\)，每個注意力頭\(h_i(i=1,...,h)\)計算方法為：
\[h_i=f(W_i^{(q)}q,W^{(k)}_ik,W^{(v)}_iv)\in R^{p_v} \]再經過另外一個線性變換\(W_o\in R^{p_o\times h p_v}\)得到最終的輸出：
\[W_o\left[ \begin{matrix} h_1\\ ...\\ h_h \end{matrix} \right] \in R^{p_o} \]
import math
import torch
from torch import nn
from d2l import torch as d2l
#@save
def transpose_qkv(X, num_heads):
"""為了多注意力頭的平行計算而變換形狀"""
# 輸入X的形狀:(batch_size，查詢或者「鍵－值」對的個數，num_hiddens)
# 輸出X的形狀:(batch_size，查詢或者「鍵－值」對的個數，num_heads，
# num_hiddens/num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 輸出X的形狀:(batch_size，num_heads，查詢或者「鍵－值」對的個數,
# num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 最終輸出的形狀:(batch_size*num_heads,查詢或者「鍵－值」對的個數,
# num_hiddens/num_heads)
# 這是為了方便在多個頭中進行平行計算而設定的
return X.reshape(-1, X.shape[2], X.shape[3])
#@save
def transpose_output(X, num_heads):
"""逆轉transpose_qkv函數的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
# 我們最後要把多個頭的堆疊在一起的，跟單個一樣的形式的
return X.reshape(X.shape[0], X.shape[1], -1)
#@save
class MultiHeadAttention(nn.Module):
"""多頭注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
# 這裡為什麼沒有分成num_heads份，是因為我平行計算的
# 可以認為原來100個nun_hiddens，5個num_heads
# 那麼我輸入就通過線性變換，每個頭的輸入都變成特徵為20
# 處理完之後每個也是特徵為20，那麼再5個在特徵維度疊加起來
# 然後直接輸入進行變換即可
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# queries，keys，values的形狀:
# (batch_size，查詢或者「鍵－值」對的個數，num_hiddens)
# valid_lens 的形狀:
# (batch_size，)或(batch_size，查詢的個數)
# 經過變換後，輸出的queries，keys，values 的形狀:
# (batch_size*num_heads，查詢或者「鍵－值」對的個數，
# num_hiddens/num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# 在軸0，將第一項（標量或者向量）複製num_heads次，
# 然後如此複製第二項，然後諸如此類。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output的形狀:(batch_size*num_heads，查詢的個數，
# num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat的形狀:(batch_size，查詢的個數，num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
# 位置編碼的實現
#@save
class PositionalEncoding(nn.Module):
"""位置編碼"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 建立一個足夠長的P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
# 就是三角函數裡面那個數值
self.P[:, :, 0::2] = torch.sin(X) # 從1到最後，間隔為1
self.P[:, :, 1::2] = torch.cos(X) # 從0到最後，間隔為2
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
# 這部分是P固定長度，X不固定，每次在P中擷取X的長度即可
return self.dropout(X)
Transformer
這一節學習的是重要的Transformer架構，因為我覺得李沐老師講得可能不夠通俗易懂，因此我將結合李宏毅老師的課程來進行講解。
總體的結構圖如下：
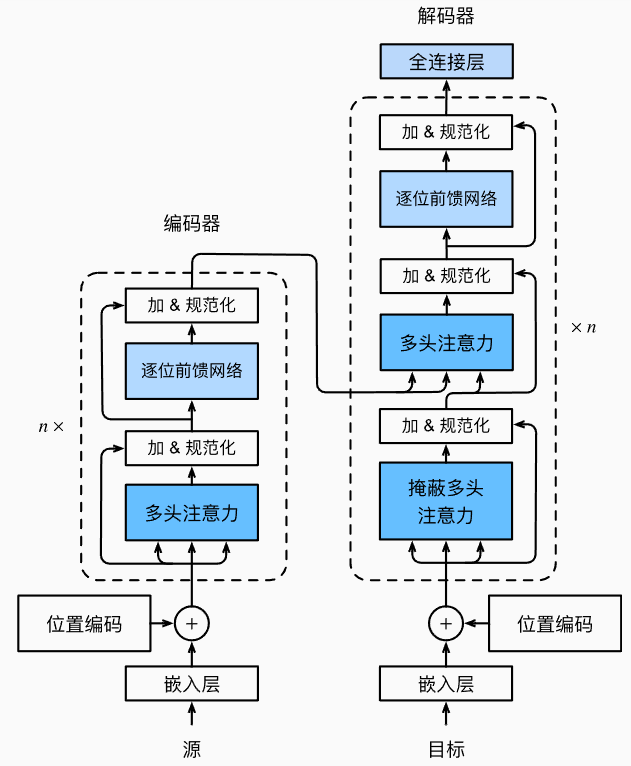
Transformer類似於seq2seq模型，也是一個Encoder和一個Decoder，將輸入的向量給Encoder進行處理，處理後的結果交給Decoder，由Decoder來決定應該輸出一個什麼樣的向量。
那麼接下來我們對其中的模組一一講解。
多頭注意力
這部分我在上一節講過，請觀看上一節的內容。
掩碼多頭注意力
這部分是因為在進行預測時，我們只能夠知道當前時刻以及之前時刻的各種資訊，我們並不能夠知道未來時刻的輸入資訊，這個Encoder中是不一樣的，因此在做attention時，在這裡我們需要根據當前的時刻，為後面時刻的內容加上掩碼，防止我們提前用到了未來的資訊，具體可以看下面這兩張圖的區別：
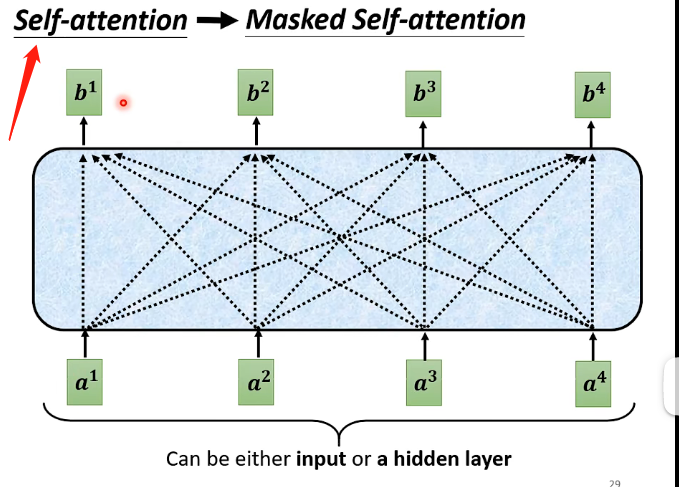
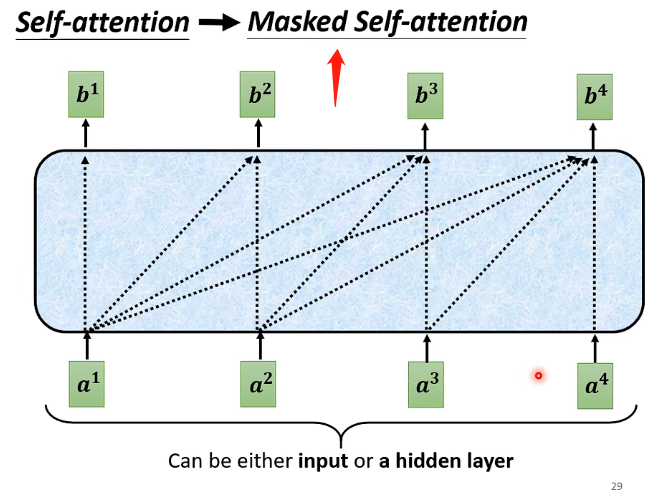
我覺得李宏毅老師的這兩張圖片形容非常恰當，很容易理解。
加&規範化
首先加就是利用了殘差連線網路的思想，即每個樣本輸入到attention後得到的向量需要加上輸入，才能夠構成輸出。
那麼規範化值得深究，常見的規範化例如批次歸一化和層歸一化，下面來探討它們在此處應用的區別：
- 批次歸一化：就可以認為我對當前這個批次（句子），它裡面含有len個樣本（len個詞語），每個詞語的維度為d，那麼我是對每一個維度進行歸一化，這是我們常見的做法，對每個維度都歸一化到均值為0方差為1。但這裡存在的問題是每個句子長度會變（len會變），那麼不同長度的句子它們自己進行歸一化，可能會使得效果不好。
- 層歸一化：它這裡跟我們之前普遍的認識不同，它是對單個樣本進行歸一化，即對單個樣本的d個維度計算均值方差然後歸一化，雖然我們認為這不同維度之間可能存在不同的數量級關係等等問題，但是在這種場合下，這種方法確實能夠克服len不同所帶來的差異，並且效果較好。
因此此處的規範化採用的是層歸一化。
基於位置的前饋網路
這部分實際上就是一個全連線層。經過前面的規範化後得到的輸入形狀為\((batch\_size, num\_len, dimention)\)，那麼要放入全連線層通常要求維度是2維，在以前我們的處理是將轉換為\((batch\_size,num\_len*dimention)\)，但是在這裡的問題是因為\(num\_len\)會變，如果這樣處理就意味著全連線層的輸入維度會發生變化，這是不行的，因此這裡的做法是轉換為\((batch\_size*num\_len，dimention)\)，保證輸入維度不發生變化， 是個數發生變化，再經過一個全連線層+ReLU+全連線層後再換回來\((batch\_size, num\_len, dimention^{\prime})\)。
資訊傳遞——Decoder中的多頭注意力
可以看到在Decoder中的多頭注意力其輸入箭頭兩個來自於Encoder的輸出，一個來自於自己的輸出。那麼其具體做法為將Encoder的輸出（最後一層）\(y_1,...,y_n\)作為這個attention的鍵和值，而查詢就來自於Decoder的目標序列經過掩碼多頭注意力的輸出（經過規範化），同時這也意味著Encoder和Decoder中輸出維度是一致的。
老師這裡指出它們的塊的個數是一致的，可能是認為是將每一個塊的編碼器的輸出作為解碼器對應塊的該attention的鍵和值，那麼在李宏毅老師的講解中它強調雖然這部分有爭議，但是大部分還是隻用編碼器最後一塊的輸出，來作為解碼器每一塊的鍵和值。
預測注意要點
在預測時，我們是將詞一個一個的輸入，也就是當輸入到第\(t\)個樣本時，由於時序的特徵，我們在進行attention時，是將前\(t-1\)個樣本作為鍵和值，而第\(t\)個樣本作為鍵和值還有查詢，然後得到第\(t\)個樣本對應的輸出的。
import math
import pandas as pd
import torch
from matplotlib import pyplot as plt
from torch import nn
from d2l import torch as d2l
# 基於位置的前饋網路的實現
class PositionWiseFFN(nn.Module):
def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,**kwargs):
super(PositionWiseFFN, self).__init__(**kwargs)
self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
# 輸入是三個維度，但是pytorch預設將前兩個合併，就達到我們的目的了
self.relu = nn.ReLU()
self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)
def forward(self,X):
return self.dense2(self.relu(self.dense1(X)))
# 殘差連線與層規範化
class AddNorm(nn.Module):
def __init__(self, normalized_shape, dropout, **kwargs):
super(AddNorm, self).__init__(**kwargs)
self.dropout = nn.Dropout(dropout)
self.ln = nn.LayerNorm(normalized_shape)
def forward(self, X, Y):
return self.ln(self.dropout(Y)+X)
# 實現編碼器的塊
class EncoderBlock(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, use_bias=False, **kwargs):
super(EncoderBlock, self).__init__(**kwargs)
self.attention = d2l.MultiHeadAttention(key_size, query_size,
value_size, num_hiddens, num_heads,
dropout, use_bias)
self.addnorm1 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens, num_hiddens)
self.addnorm2 = AddNorm(norm_shape, dropout)
def forward(self, X, valid_len):
Y = self.addnorm1(X, self.attention(X,X,X,valid_len))
return self.addnorm2(Y,self.ffn(Y))
# 實現編碼器
class TransformerEncoder(d2l.Encoder):
def __init__(self, vocab_size, key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
num_heads, num_layers, dropout, use_bias=False, **kwargs):
super(TransformerEncoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
# 詞嵌入第一個引數為我們有多少個需要表示的詞，第二個為我們要用多少個維度來表示一個單詞
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module("block"+str(i),
EncoderBlock(key_size, query_size, value_size,
num_hiddens,norm_shape,ffn_num_input,
ffn_num_hiddens,num_heads,dropout,
use_bias))
def forward(self, X, valid_len, *args):
# 因為位置編碼值在-1和1之間，而embedding通常會將d維度變成範數為1，那麼就可能d大的時候元素大小很小
# 因此嵌入值乘以嵌入維度的平方根進行縮放，使得差不多跟位置編碼大小
# 然後再與位置編碼相加。
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self.attention_weights = [None] * len(self.blks)
for i, blk in enumerate(self.blks):
X = blk(X, valid_len) # 計算該塊的輸出並作為下一層的輸入
self.attention_weights[i] = blk.attention.attention.attention_weights
return X
# 實現解碼器塊
class DecoderBlock(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
dropout, i, **kwargs):
super(DecoderBlock, self).__init__(**kwargs)
self.i = i
self.attention1 = d2l.MultiHeadAttention(key_size, query_size, value_size,
num_hiddens, num_heads, dropout)
self.addnorm1 = AddNorm(norm_shape,dropout)
self.attention2 = d2l.MultiHeadAttention(key_size, query_size, value_size,
num_hiddens, num_heads, dropout)
self.addnorm2 = AddNorm(norm_shape, dropout)
self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens, num_hiddens)
self.addnorm3 = AddNorm(norm_shape, dropout)
def forward(self, X, state):
# 前兩個分別為編碼器的輸出和有效長度
enc_outputs, enc_valid_lens = state[0],state[1]
# 訓練階段，輸出序列的所有詞元都在同一時間處理，
# 因此state[2][self.i]初始化為None。
# 預測階段，輸出序列是通過詞元一個接著一個解碼的，
# 因此state[2][self.i]包含著直到當前時間步第i個塊解碼的輸出表示
if state[2][self.i] is None:
key_values = X
else:
key_values = torch.cat((state[2][self.i], X), axis=1)
# 在預測時儲存著當前時間步包括之前的x，來作為key和value
state[2][self.i] = key_values # 更新
if self.training:
batch_size, num_steps, _ = X.shape
# dec_valid_lens的開頭:(batch_size,num_steps),用來做掩碼attention
# 其中每一行是[1,2,...,num_steps]
dec_valid_lens = torch.arange(1, num_steps+1, device=X.device).repeat(batch_size,1)
else:
dec_valid_lens = None # 在預測的時候不關心這個，因為是一個一個進來的
X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
Y = self.addnorm1(X,X2)
Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
Z = self.addnorm2(Y,Y2)
return self.addnorm3(Z,self.ffn(Z)), state
# 完成的transformer解碼器
class TransformerDecoder(d2l.AttentionDecoder):
def __init__(self,vocab_size, key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, num_layers,
dropout, **kwargs):
super(TransformerDecoder, self).__init__(**kwargs)
self.num_hiddens = num_hiddens
self.num_layers = num_layers
self.embedding = nn.Embedding(vocab_size, num_hiddens)
self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
self.blks = nn.Sequential()
for i in range(num_layers):
self.blks.add_module("block"+str(i), DecoderBlock(key_size, query_size, value_size,
num_hiddens, norm_shape, ffn_num_input,
ffn_num_hiddens, num_heads, dropout, i))
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, enc_valid_lens, *args):
return [enc_outputs, enc_valid_lens, [None]*self.num_layers]
def forward(self, X, state):
X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
self._attention_weights = [[None] * len(self.blks) for _ in range(2)]
for i, blk in enumerate(self.blks):
X, state = blk(X, state)
self._attention_weights[0][
i] = blk.attention1.attention.attention_weights
# 「編碼器－解碼器」自注意力權重
self._attention_weights[1][
i] = blk.attention2.attention.attention_weights
return self.dense(X), state
@property
def attention_weights(self):
return self._attention_weights
if __name__ == "__main__":
num_hiddens, num_layers, dropout, batch_size, num_steps = 32, 2, 0.1, 64, 10
lr, num_epochs, device = 0.005, 200, d2l.try_gpu()
ffn_num_input, ffn_num_hiddens, num_heads = 32, 64, 4
key_size, query_size, value_size = 32, 32, 32
norm_shape = [32]
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = TransformerEncoder(len(src_vocab), key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,num_layers, dropout)
decoder = TransformerDecoder(len(tgt_vocab), key_size, query_size, value_size, num_hiddens,
norm_shape, ffn_num_input, ffn_num_hiddens, num_heads, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
plt.show()
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, dec_attention_weight_seq = d2l.predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps, device, True)
print(f'{eng} => {translation}, ',
f'bleu {d2l.bleu(translation, fra, k=2):.3f}')
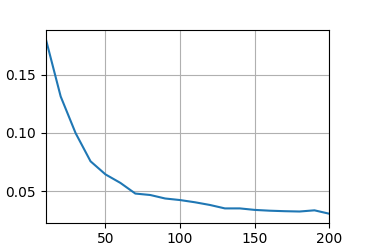
loss 0.031, 4096.8 tokens/sec on cuda:0
go . => va !, bleu 1.000
i lost . => je perdu ., bleu 0.687
he's calm . => il est calme ., bleu 1.000
i'm home . => je suis chez moi ., bleu 1.000
很多次預測的BELU都達到了1.0。
小結：
- transformer是編碼器－解碼器架構的一個實踐，儘管在實際情況中編碼器或解碼器可以單獨使用。
- 在transformer中，多頭自注意力用於表示輸入序列和輸出序列，不過解碼器必須通過掩蔽機制來保留自迴歸屬性。
- transformer中的殘差連線和層規範化是訓練非常深度模型的重要工具。
- transformer模型中基於位置的前饋網路使用同一個多層感知機，作用是對所有序列位置的表示進行轉換。
自然語言處理：預訓練
要理解文字，我們應該先學習它如何進行表示。利用來自大型語料庫的現有文字序列，我們可以通過自監督學習來預訓練文字表示，例如通過使用周圍文字的其他部分來預測文字的隱藏部分，這樣模型可以在海量資料中學習資訊， 而不需要昂貴的標籤標註。
詞嵌入（Word2vec）
將單詞對映到實向量的技術稱為詞嵌入。
在之前我們用過one-hot編碼來進行表示，但雖然one-hot編碼很容易構建，但它們並不是一個很好的選擇，因為獨特向量不能夠準確表達不同詞之間的相似度，例如計算相似度的「餘弦相似度」，對於兩個向量，它們之間的相似度就是它們角度的餘弦：
\[\frac{X^TY}{\Vert X\Vert \Vert Y \Vert}\in [-1,1]
\]
但是獨熱編碼任意兩個不同的詞向量之間計算餘弦相似度都為0，因此它不能夠編碼詞之間的相關性。
由於上述問題，因此誕生了word2vec工具，它將每個詞對映到一個固定長度的向量，這些向量可以更好地表示不同次之間的相似性和類比關係。其包含兩個模型，即跳元模型和連續詞袋，都屬於自監督模型。下面將進行簡要介紹。
跳元模型（Skip-Gram）
該模型假設一個詞可以用來在文字序列中生成其周圍的單詞，例如文字序列"the man loves his son"，假設中心詞選擇"love"，其上下視窗設定為2，那麼跳元模型考慮生成其上下文詞的條件概率為：
\[P(the,man,his,son\mid loves)
\]
而若再假設上下文詞都是給定中心詞的情況下獨立生成的，可寫成：
\[P(the \mid loves)·P(man \mid loves)·P(his \mid loves)·P(son \mid loves)·
\]
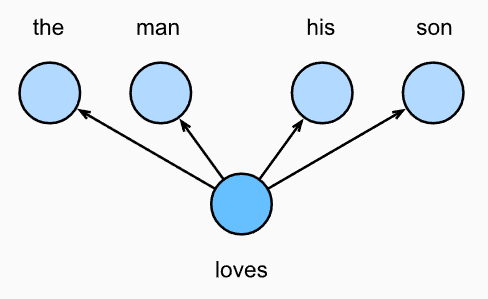
在跳元模型中，每個詞都有兩個d維向量來表示，對於詞典中索引為i的任何詞，分別用$v_i\in R^d、u_i\in R^d \(來表示其用作中心詞和上下文詞時的兩個向量。那麼假設給定中心詞\)w_c\(，生成其上下文詞\)w_o$，條件概率計算為：
\[P(w_o\mid w_c)=\frac{\exp(u_o^Tv_c)}{\sum_{i\in V}\exp(u_i^T v_c)}
\]
其中V是所有詞典的意思。那麼前面我們也提到上下文視窗的意義，因此給定長度為T的文字序列，假設上下文詞是在給定任何中心詞的情況下獨立生成的，那麼對於上下文視窗m，跳元模型的似然函數就是在給定任何中心詞的情況下生成所有上下文詞的概率：
\[\prod_{t=1}^T \prod_{-m \leq j \leq m~j\neq 0}P(w^{(t+j)}\mid w^{(t)})
\]
在訓練時也是通過最大化似然函數來學習模型引數。
連續詞袋（CBOW）
它與跳元模型最主要的區別在於其假設中心詞是基於其在文字序列中的周圍上下文詞所生成的，即：
\[P(love\mid the,man,his,son)
\]
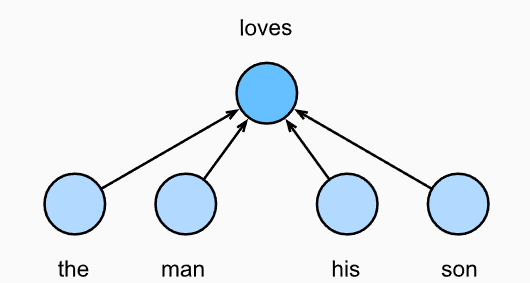
而由於對單個詞的生成存在多個上下文詞，因此需要取平均。對於字典中索引為i的任意詞，用$v_i\in R^d、u_i\in R^d $來表示其用作上下文和中心詞時的兩個向量（與跳元模型相反），那麼：
\[P(w_c\mid w_{o1},...,w_{o2m})=\frac{\exp(\frac{1}{2m}u_c^T(v_{o1}+...+v_{o2m}))}{\sum_{i\in V}\exp(\frac{1}{2m}u_i^T(v_{o1}+...+v_{o2m}))}
\]
同樣，給定長度為T的文字序列，其似然函數為：
\[\prod _{t=1}^T P(w^{(t)}\mid w^{(t-m)},...,w^{(t-1)},w^{(t+1)},...,w^{(t+m)})
\]
小結：
- 詞向量是用於表示單詞意義的向量，也可以看作是詞的特徵向量。將詞對映到實向量的技術稱為詞嵌入。
- word2vec工具包含跳元模型和連續詞袋模型。
- 跳元模型假設一個單詞可用於在文字序列中，生成其周圍的單詞；而連續詞袋模型假設基於上下文詞來生成中心單詞。
近似訓練
在上一節的討論中，我們可以發現兩種模型的似然函數都含有對完整詞典的求和項，這在實際中計算的開銷太大，因此需要進行優化。為了降低上述計算的複雜度，下面介紹兩種近似訓練方法：負取樣和分層softmax（以跳元模型為例子）
負取樣
負取樣首先修改了原目標函數。給定中心詞\(w_c\)的上下文視窗，任意上下文詞\(w_o\)屬於該視窗的被認為是如下事件的概率：
\[P(D=1\mid w_c,w_o)=\sigma (u_o^Tv_c)=\frac{1}{1+\exp(u_o^Tv_c)}
\]
同樣似然函數為：
\[\prod_{t=1}^T\prod_{-m\leq j\leq m ~j\neq0}P(D=1\mid w^{(t)},w^{(t+j)})
\]
但是這樣第一個連乘符號只考慮了位於視窗內的上下文詞，可以認為我們在訓練時沒有考慮負樣本，只考慮了正樣本，因此我們需要增加負樣本來進行學習。
用S來表示上下文詞\(w_o\)來自於中心詞\(w_c\)的上下文視窗的事件。然後從預定義分佈\(P(w)\)中取樣K個不是來自於這個上下文視窗的噪聲詞\(w_k(k=1,2,...,K)\)。用\(N_k\)表示\(w_k\)不是來自於該上下文視窗的事件。因此重寫為：
\[\prod_{t=1}^T \prod_{-m \leq j \leq m~j\neq 0}P(w^{(t+j)}\mid w^{(t)})\\
P(w^{(t+j)}\mid w^{(t)})=P(D=1\mid w^{(t)},w^{(t+j)})·\prod_{k=1,w_k\in P(w)}^K P(D=0\mid w^{(t)},w_k)
\]
訓練以上的似然函數最大化即可。
層序softmax
這一部分比較抽象，簡單理解應該就是將計算複雜度降為詞表大小的對數級別。
小結：
- 負取樣通過考慮相互獨立的事件來構造損失函數，這些事件同時涉及正例和負例。訓練的計算量與每一步的噪聲詞數成線性關係。
- 分層softmax使用二元樹中從根節點到葉節點的路徑構造損失函數。訓練的計算成本取決於詞表大小的對數。
本筆記可能存在未記錄的章節，我也是捨棄一部分內容的學習，後續有時間會補上的。