萬字 HashMap 詳解，基礎（優雅）永不過時

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

前言

大家好，我是小彭。

在上一篇文章裡，我們聊到了雜湊表的整體設計思想，在後續幾篇文章裡，我們將以 Java 語言為例，分析標準庫中實現的雜湊表實現，包括 HashMap、ThreadLocalMap、LinkedHashMap 和 ConcurrentHashMap。
今天，我們來討論 Java 標準庫中非常典型的雜湊表結構，也是「面試八股文」的標準題庫之一 —— HashMap。

本文原始碼基於 Java 8 HashMap，並關聯分析部分 Java 7 HashMap。

小彭的 Android 交流群 02 群已經建立啦，掃描文末二維條碼進入~

思維導圖：

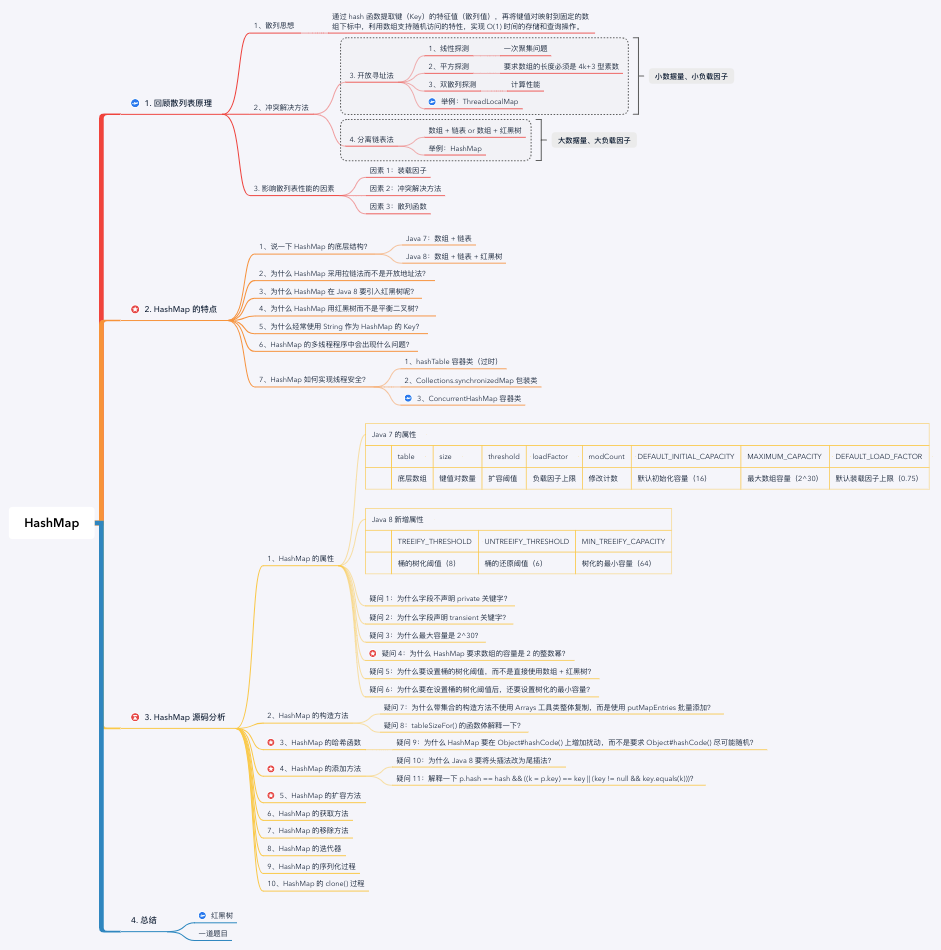
1. 回顧雜湊表工作原理

在分析 HashMap 的實現原理之前，我們先來回顧雜湊表的工作原理。

雜湊表是基於雜湊思想實現的 Map 資料結構，將雜湊思想應用到雜湊表資料結構時，就是通過 hash 函數提取鍵（Key）的特徵值（雜湊值），再將鍵值對對映到固定的陣列下標中，利用陣列支援隨機存取的特性，實現 O(1) 時間的儲存和查詢操作。

雜湊表示意圖

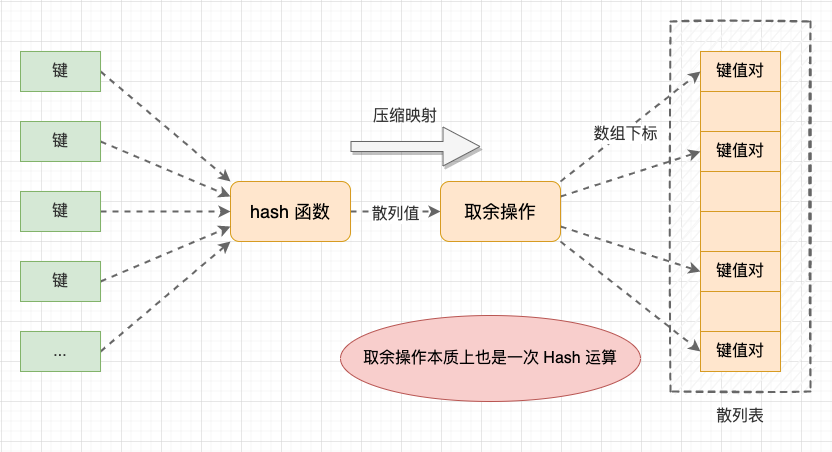
在從鍵值對對映到陣列下標的過程中，雜湊表會存在 2 次雜湊衝突：

第 1 次 - hash 函數的雜湊衝突： 這是一般意義上的雜湊衝突；
第 2 次 - 雜湊值取餘轉陣列下標： 本質上，將雜湊值轉陣列下標也是一次 Hash 演演算法，也會存在雜湊衝突。同時，這也說明 HashMap 中同一個桶中節點的雜湊值不一定是相同的。

事實上，由於雜湊表是壓縮對映，所以我們無法避免雜湊衝突，只能保證雜湊表不會因為雜湊衝突而失去正確性。常用的雜湊衝突解決方法有 2 類：

開放定址法： 例如 ThreadLocalMap；
分離連結串列法： 例如今天要分析的 HashMap 雜湊表。

分離連結串列法（Separate Chaining）的核心思想是： 在出現雜湊衝突時，將衝突的元素新增到同一個桶（Bucket / Slot）中，桶中的元素會組成一個連結串列，或者跳錶、紅黑樹等動態資料結構。相比於開放定址法，連結串列法是更常用且更穩定的衝突解決方法。

分離連結串列法示意圖

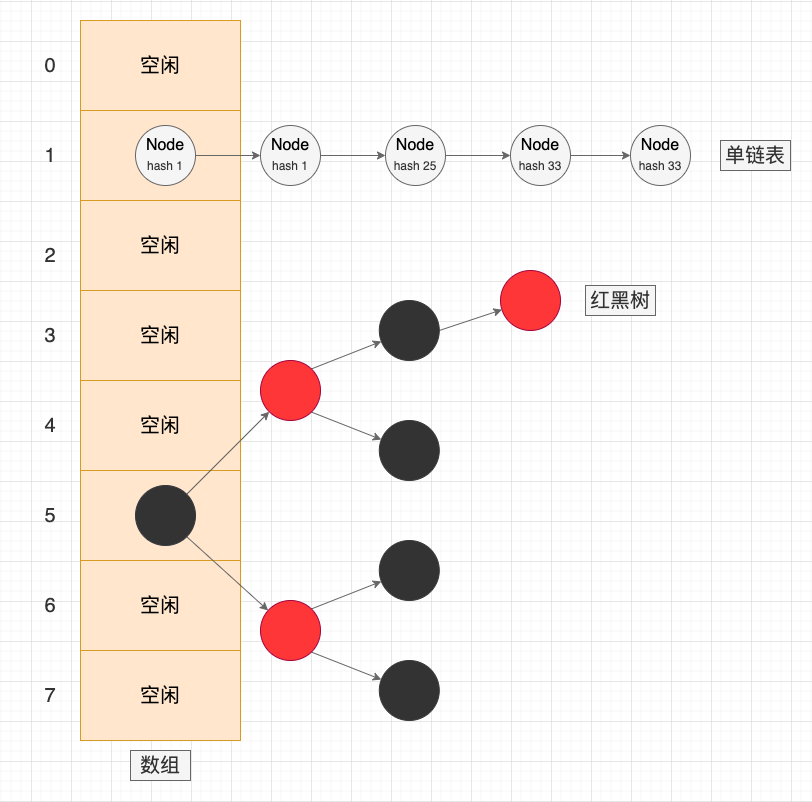
影響雜湊表效能的關鍵在於「雜湊衝突的發生概率」，衝突概率越低，時間複雜度越接近於 O(1)。那麼，哪些因素會影響衝突概率呢？主要有 3 個：

因素 1 - 裝載因子： 裝載因子 (Load Factor) = 雜湊表中鍵值對數目 / 雜湊表的長度。隨著雜湊表中元素越來越多，空閒位置越來越少，就會導致雜湊衝突的發生概率越來越大，使得雜湊表操作的平均時間會越來越大；
因素 2 - 採用的衝突解決方法： 開放定址法的衝突概率天然比分離連結串列法高，適合於小資料量且裝載因子較小的場景；分離連結串列法對裝載因子的容忍度更高，適合於巨量資料量且大物件（相對於一個指標）的場景；
因素 3 - 雜湊函數設計： 雜湊演演算法隨機性和高效性也會影響雜湊表的效能。如果雜湊值不夠隨機，即使雜湊表整體的裝載因子不高，也會使得資料聚集在某一個區域或桶內，依然會影響雜湊表的效能。

2. 認識 HashMap 雜湊表

2.1 說一下 HashMap 的底層結構？

HashMap 是基於分離連結串列法解決雜湊衝突的動態雜湊表：

在 Java 7 中使用的是「陣列 + 連結串列」，發生雜湊衝突的鍵值對會用頭插法新增到單連結串列中；
在 Java 8 中使用的是「陣列 + 連結串列 + 紅黑樹」，發生雜湊衝突的鍵值對會用尾插法新增到單連結串列中。如果連結串列的長度大於 8 時且雜湊表容量大於 64，會將連結串列樹化為紅黑樹。在擴容再雜湊時，如果紅黑樹的長度低於 6 則會還原為連結串列；
HashMap 的陣列長度保證是 2 的整數冪，預設的陣列容量是 16，預設裝載因子上限是 0.75，擴容閾值是 12（16*0.75）；
在建立 HashMap 物件時，並不會建立底層陣列，這是一種懶初始化機制，直到第一次 put 操作才會通過 resize() 擴容操作初始化陣列;
HashMap 的 Key 和 Value 都支援 null，Key 為 null 的鍵值對會對映到陣列下標為 0 的桶中。

2.2 為什麼 HashMap 採用拉鍊法而不是開放地址法？

我認為 Java 給予 HashMap 的定位是一個相對「通用」的雜湊表容器，它應該在面對各種輸入場景中都表現穩定。

開放地址法的雜湊衝突發生概率天然比分離連結串列法更高，所以基於開放地址法的雜湊表不能把裝載因子的上限設定得很高。在儲存相同的資料量時，開放地址法需要預先申請更大的陣列空間，記憶體利用率也不會高。因此，開放地址法只適合小資料量且裝載因子較小的場景。

而分離連結串列法對於裝載因子的容忍度更高，能夠適合巨量資料量且更高的裝載因子上限，記憶體利用率更高。雖然連結串列節點會多消耗一個指標記憶體，但在一般的業務場景中可以忽略不計。

我們可以舉個反例，在 Java 原生的資料結構中，也存在使用開放地址法的雜湊表 —— 就是 ThreadlLocal。因為專案中不會大量使用 ThreadLocal 執行緒區域性儲存，所以它是一個小規模資料場景，這裡使用開放地址法是沒問題的。

2.3 為什麼 HashMap 在 Java 8 要引入紅黑樹呢？

因為當雜湊衝突加劇的時候，在連結串列中尋找對應元素的時間複雜度是 O(K)，K 是連結串列長度。在極端情況下，當所有資料都對映到相同連結串列時，時間複雜度會「退化」到 O(n)。

而使用紅黑樹（近似平衡的二元搜尋樹）的話，樹形結構的時間複雜度與樹的高度有關， 查詢複雜度是 O(lgK)，最壞情況下時間複雜度是 O(lgn)，時間複雜度更低。

2.4 為什麼 HashMap 使用紅黑樹而不是平衡二元樹？

這是在查詢效能和維護成本上的權衡，紅黑樹和平衡二元樹的區別在於它們的平衡程度的強弱不同：

平衡二元樹追求的是一種 「完全平衡」 狀態：任何結點的左右子樹的高度差不會超過 1。優勢是樹的結點是很平均分配的；

紅黑樹不追求這種完全平衡狀態，而是追求一種 「弱平衡」 狀態：整個樹最長路徑不會超過最短路徑的 2 倍。優勢是雖然犧牲了一部分查詢的效能效率，但是能夠換取一部分維持樹平衡狀態的成本。

2.5 為什麼經常使用 String 作為 HashMap 的 Key？

1、不可變類 String 可以避免修改後無法定位鍵值對： 假設 String 是可變類，當我們在 HashMap 中構建起一個以 String 為 Key 的鍵值對時，此時對 String 進行修改，那麼通過修改後的 String 是無法匹配到剛才構建過的鍵值對的，因為修改後的 hashCode 可能會變化，而不可變類可以規避這個問題；
2、String 能夠滿足 Java 對於 hashCode() 和 equals() 的通用約定： 既兩個物件 equals() 相同，則 hashCode() 相同，如果 hashCode() 相同，則 equals() 不一定相同。這個約定是為了避免兩個 equals() 相同的 Key 在 HashMap 中儲存兩個獨立的鍵值對，引起矛盾。

2.6 HashMap 的多執行緒程式中會出現什麼問題？

資料覆蓋問題：如果兩個執行緒並行執行 put 操作，並且兩個資料的 hash 值衝突，就可能出現資料覆蓋（執行緒 A 判斷 hash 值位置為 null，還未寫入資料時掛起，此時執行緒 B 正常插入資料。接著執行緒 A 獲得時間片，由於執行緒 A 不會重新判斷該位置是否為空，就會把剛才執行緒 B 寫入的資料覆蓋掉）。事實上，這個未同步資料在任意多執行緒環境中都會存在這個問題；
環形連結串列問題： 在 HashMap 觸發擴容時，並且正好兩個執行緒同時在操作同一個連結串列時，就可能引起指標混亂，形成環型鏈條（因為 Java 7 版本採用頭插法，在擴容時會翻轉連結串列的順序，而 Java 8 採用尾插法，再擴容時會保持連結串列原本的順序）。

2.7 HashMap 如何實現執行緒安全？

有 3 種方式：

方式 1 - 使用 hashTable 容器類（過時）： hashTable 是執行緒安全版本的雜湊表，它會在所有方法上增加 synchronized 關鍵字，且不支援 null 作為 Key。
方法 2 - 使用 Collections.synchronizedMap 包裝類： 原理也是在所有方法上增加 synchronized 關鍵字；
方法 3 - 使用 ConcurrentHashMap 容器類： 基於 CAS 無鎖 + 分段實現的執行緒安全雜湊表；

3. HashMap 的屬性

在分析 HashMap 的執行流程之前，我們先用一個表格整理 HashMap 的屬性：

版本	資料結構	節點實現類	屬性
Java 7	陣列 + 連結串列	Entry（單連結串列）	1、table（陣列） 2、size（尺寸） 3、threshold（擴容閾值） 4、loadFactor（裝載因子上限） 5、modCount（修改計數） 6、預設陣列容量 16 7、最大陣列容量 2^30 8、預設負載因子 0.75
Java 8	陣列 + 連結串列 + 紅黑樹	1、Node（單連結串列） 2、TreeNode（紅黑樹）	9、桶的樹化閾值 8 10、桶的還原閾值 6 11、最小樹化容量閾值 64

HashMap.java

public class HashMap<K,V> extends AbstractMap<K,V>
    implements Map<K,V>, Cloneable, Serializable {

    // 預設陣列容量
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

    // 疑問 3：為什麼最大容量是 2^30 次冪？
    // 疑問 4：為什麼 HashMap 要求陣列的容量是 2 的整數冪？
    // 陣列最大容量：2^30（高位 0100，低位都是 0）
    static final int MAXIMUM_CAPACITY = 1 << 30;

    // 預設負載因子：0.75
    static final float DEFAULT_LOAD_FACTOR = 0.75f;

    // 疑問 5：為什麼要設定桶的樹化閾值，而不是直接使用陣列 + 紅黑樹？
    // （Java 8 新增）桶的樹化閾值：8
    static final int TREEIFY_THRESHOLD = 8;

    // （Java 8 新增）桶的還原閾值：6（在擴容時，當原有的紅黑樹內數量 <= 6時，則將紅黑樹還原成連結串列）
    static final int UNTREEIFY_THRESHOLD = 6;

    // 疑問 6：為什麼要在設定桶的樹化閾值後，還要設定樹化的最小容量？
    // （Java 8 新增）樹化的最小容量：64（只有整個雜湊表的長度滿足最小容量要求時才允許連結串列樹化，否則會直接擴容，而不是樹化）
    static final int MIN_TREEIFY_CAPACITY = 64;

    // 底層陣列（每個元素是一個單連結串列或紅黑樹）
    transient Node<K,V>[] table;

    // entrySet() 返回值快取
    transient Set<Map.Entry<K,V>> entrySet;

    // 有效鍵值對數量
    transient int size;

    // 擴容閾值（容量 * 裝載因子）
    int threshold;		

    // 裝載因子上限
    final float loadFactor;

    // 修改計數
    transient int modCount;

    // 連結串列節點（一個 Node 等於一個鍵值對）
    static class Node<K,V> implements Map.Entry<K,V> {
        // 雜湊值（相同連結串列上 Key 的雜湊值可能相同）
        final int hash;
        // Key（一個雜湊表上 Key 的 equals() 一定不同）
        final K key;
        // Value（Value 不影響節點位置）
        V value;
        Node<K,V> next;

        Node(int hash, K key, V value, Node<K,V> next) {
            this.hash = hash;
            this.key = key;
            this.value = value;
            this.next = next;
        }

        // Node 的 hashCode 取 Key 和 Value 的 hashCode
        public final int hashCode() {
            return Objects.hashCode(key) ^ Objects.hashCode(value);
        }

        // 兩個 Node 的 Key 和 Value 都相等，才認為相等
        public final boolean equals(Object o) {
            if (o == this)
                return true;
            if (o instanceof Map.Entry) {
                Map.Entry<?,?> e = (Map.Entry<?,?>)o;
                if (Objects.equals(key, e.getKey()) &&
                    Objects.equals(value, e.getValue()))
                    return true;
            }
            return false;
        }
    }
		
    // （Java 8 新增）紅黑樹節點
    static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
        // 父節點
        TreeNode<K,V> parent;
        // 左子節點
        TreeNode<K,V> left;
        // 右子節點
        TreeNode<K,V> right;
        // 刪除輔助節點
        TreeNode<K,V> prev;
        // 顏色
        boolean red;

        TreeNode(int hash, K key, V val, Node<K,V> next) {
            super(hash, key, val, next);
        }

        // 返回樹的根節點
        final TreeNode<K,V> root() {
            for (TreeNode<K,V> r = this, p;;) {
                if ((p = r.parent) == null)
                    return r;
                r = p;
            }
        }
    }
}

LinkedHashMap.java

static class Entry<K,V> extends HashMap.Node<K,V> {
    Entry<K,V> before, after;
    Entry(int hash, K key, V value, Node<K,V> next) {
        super(hash, key, value, next);
    }
}

相比於線性表，HashMap 的屬性可算是上難度了，HashMap 真卷。不出意外的話又有小朋友出來舉手提問了