博迪投資學·資本市場：第9、14、16章的模型總結

第九章：資本資產定價模型

資本資產定價模型(CPM)是現代金融經濟學的莫基石。該模型對資產風險與其期望收益之間的關係給出了精準的預測。

資本資產定價模型的一個關鍵觀點是：因為市場組合是所有風險組合的加總，市場組合內的資產比例也是投資者的持有比例。所以，如果所有投資者選擇相同的風險資產組合，這個組合一定是市場組合，即可投資集中所有資產以市值加權平均得到的組合。因而，基於每個投資者最優風險資產組合之上的資產設定線實際上就是圖9-1b所顯示的資本市場線。這個應用讓我們能夠就風險回報權衡做更多的發揮。

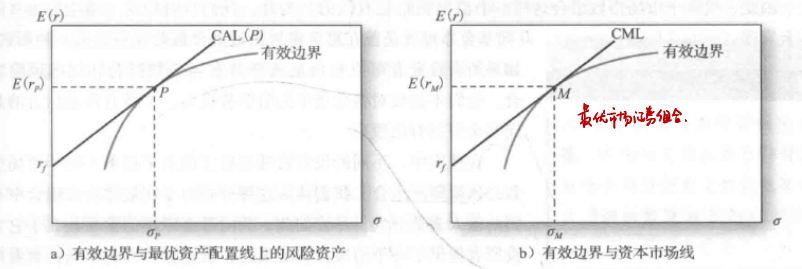
我們將整個市場看作是一個風險資產組合，所以能夠得到【9-1】

\[y=\frac{E\left(r_{M}\right)-r_{f}}{A \sigma_{M}^{2}} \]

那麼市場組合的風險溢價（期望超額收益）：

\[E\left(R_{M}\right)=E\left(r_{M}\right)-r_{f} \]

另外市場投資組合的風險溢價與其方差和平均風險厭惡水平有關。【9-2】

\[E\left(R_{M}\right)=\bar{A} \sigma_{M}^{2} \]

根據公式【7-16】我們可以計算出某隻股票對於市場組合方差的貢獻：【9-3】

\[w_{\mathrm{GE}}\left[w_{1} \operatorname{Cov}\left(R_{1}, R_{\mathrm{GE}}\right)+w_{2} \operatorname{Cov}\left(R_{2}, R_{\mathrm{GE}}\right)+\cdots+w_{\mathrm{GE}} \operatorname{Cov}\left(R_{\mathrm{GE}}, R_{\mathrm{GE}}\right)+\cdots+w_{n} \operatorname{Cov}\left(R_{n}, R_{\mathrm{GE}}\right)\right] \]

我們注意到【9-4】

\[\sum_{i=1}^{n} w_{i} \operatorname{Cov}\left(R_{i}, R_{\mathrm{GE}}\right)=\sum_{i=1}^{n} \operatorname{Cov}\left(w_{i} R_{i}, R_{G E}\right)=\operatorname{Cov}\left(\sum_{i=1}^{n} w_{i} R_{i}, R_{\mathrm{GE}}\right) \]

又有

\[\sum_{i=1}^{n} w_{i} R_{i}=R_M \]

所以

\[\sum_{i=1}^{n} w_{i} \operatorname{Cov}\left(R_{i}, R_{\mathrm{GE}}\right)=\operatorname{Cov}\left(R_{M}, R_{\mathrm{GE}}\right) \]

所以最終我們可以得到

通用公司股票對市場投資組合方差的貢獻程度

\[w_{GE}\operatorname{Cov}\left(R_{GE}, R_{\mathrm{M}}\right) \]

同時也可以看到，我們持有通用電氣公司股票對整個市場投資組合的風險溢價的貢獻為

\[w_{GE}E(R_{GE}) \]

投資通用電氣公司股票的回報一風險比率可以表達為：$\frac{E\left(R_{\mathrm{GE}}\right)}{\operatorname{Cov}\left(R_{\mathrm{GE}}, R_{M}\right)}$

模型【9-5】：投資於市場投資組合的回報一風險比:

\[ \frac{\text { 市場風險溢價 }}{\text { 市場方差 }}=\frac{E\left(R_{M}\right)}{\sigma_{M}^{2}} \]

公式(9-5)中的比率通常也叫作風險的市場價格(market price of risk),

市場會讓投資某一股票的風險回報率和投資市場整體的投資回報率相等，所以有【9-6】

\[\frac{E\left(R_{\mathrm{GE}}\right)}{\operatorname{Cov}\left(R_{\mathrm{GE}}, R_{M}\right)}=\frac{E\left(R_{\mathrm{M}}\right)}{\sigma_{M}^{2}} \]

對9-6進行變換得到

模型【9-7】：測算一隻股票的合理風險溢價

\[E\left(R_{\mathrm{CE}}\right)=\frac{\operatorname{Cov}\left(R_{\mathrm{CE}}, R_{M}\right)}{\sigma_{M}^{2}}\left[E\left(R_{M}\right)\right] \]

這裡$\text{Cov}(r_{GE},r_M)/σ_M^2$，這一比率衡量了通用電氣公司股票對市場投資組合方差的貢獻程度，是
市場投資組合方差的組成部分。這一比率也叫作貝塔，用$\beta$表示。這樣，式(9-7)可以表示為：

模型【9-8】：期望收益-貝塔關係(expected return-beta relationship)

\[E\left(r_{\mathrm{GE}}\right)=r_{f}+\beta_{\mathrm{GE}}\left[E\left(r_{M}\right)-r_{f}\right] \]

這個期望收益-貝塔關係(expected return-beta relationship)就是資本資產定價模型最為普通的種表達方式。

將上式每一行進行加總即得出所有資產組合的資本資產定價模型，因為這裡$E\left(r_{p}\right)=\sum_{k} w_{k} E\left(r_{k}\right)$是資產組合的期望收益，$\beta_{P}=\sum_{k} w_{k} \beta_{k}$是資產組合的貝塔值。另外，這一結果對市場組合本身也是有效的：

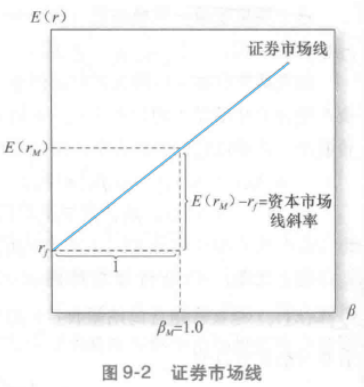
期望收益-貝塔關係就是證券市場線(security marketline,SML),如圖9-2所示。因為市場的貝塔值為1，其斜率就是市場投資組合的風險溢價，橫軸為B值，縱軸為期望收益，當橫軸的B=1時，這一點就是市場投資組合的期望收益率。

相比較而言，證券市場線刻畫的是單個風險資產的風險溢價，它是該資產風險的一個函數。作為高度分散化資產組合一部分的單項資產的風險測度並不是資產的標準差或方差，而是該資產對資產組合方差的貢獻程度，我們用貝塔值來測度這一貢獻程度。證券市場線對有效資產組合和單項資產均適用。

在給定貝塔值的情況下，其期望收益高於根據資本資產定價模型所得出的收益值。被高估的股票的期望收益低於證券市場線上所給出的正常收益值。

股票的實際期望收益與正常期望收益之間的差，我們稱為股票的阿爾法(alpha),記作a。

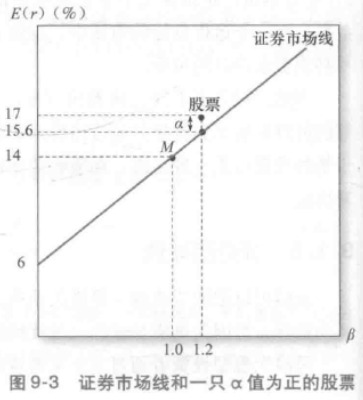
由式(8-11)可知任意一隻股票的超額收益，所以我們從這個等式出發。

模型【9-9】：一隻股票的超額收益

\[R_{i}=\alpha_{i}+\beta_{i} R_{M}+e_{i} \]

$e_{i}$ 是對每個公司特異性的、以 0 為均值的殘差項, 並與股票和市場因素 $R_{M}$ 無關。殘差代表分散化的、非系統性的, 或者特異的風險。一個股票的總風險由系統性影響 $\beta_{i} R_{M} $ 的方差和 $e_{i}$ 的方差衡量。總而言之, 風險溢價 (平均超額收益) 和方差為:

模型【9-10】：一隻股票的風險溢價和方差由市場β計算

\[\begin{aligned} E\left(R_{i}\right) &=\alpha_{i}+\beta_{i} E\left(R_{M}\right) \\ \alpha_{i}^{2} &=\beta_{i}^{2} \sigma_{M}^{2}+\sigma^{2}\left(e_{i}\right) \end{aligned} \]

模型【9-11】：對於N只股票的組合的收益率

\[R_{Q}=\sum_{k=1}^{N} w_{k} \alpha_{k}+\sum_{k=1}^{N} w_{k} \beta_{k} R_{M}+\sum_{k=1}^{N} w_{k} e_{k}=\alpha_{Q}+\beta_{Q} R_{M}+e_{Q} \]

模型【9-12】：資本資產定價模型式

\[E\left(r_{i}\right)-E\left(r_{z}\right)=\left[E\left(R_{M}\right)-E\left(R_{z}\right)\right] \frac{\operatorname{Cov}\left(r_{i}, r_{M}\right)}{\sigma_{M}^{2}}=\beta_{i}\left[E\left(r_{M}\right)-E\left(r_{z}\right)\right] \]

第十一章：有效市場假說

弱式有效市場假說(weak-form EMH)認為，股價已經反映了全部能從市場交易資料中獲得的信
息，這些資訊包括歷史股價、交易量、未平倉量等。【歷史資訊】

半強式有效市場假說(semistrong-form EMH)認為，與公司前景有關的全部公開的已知資訊一
定已經在股價中反映出來了。【公開資訊】

最後，強式有效市場假說(strong-form EMH)認為，股價反映了全部與市場相關的資訊，甚至
包括僅公司內部人員知道的資訊。【完全所有資訊】

基本面分析(fundamental analysis)是利用公司的盈利、股利前景、未來利率的預期以及公司的風險評估來決定適當的股票價格。最終，它表達了一種股東將獲得的每股收益的貼現值的意圖。如果該價值超過了股價，基本面分析師將推薦購買該股票。

第十四章：債權的價格與收益

債券(debt securities)是對特定時期收入流的索取權。債券通常被稱為固定收益證券，因為債饋券代表了固定的或者是根據特定公式計算的收益流入的承諾。由於支付方式已預先約定，這類證券相對而言更容易被理解。只要發行人的信譽有保障，債券的風險就是最小的。這些特徵使得債券成為我們分析全部可能投資工具的便捷起點。

債券(bod)是關於借貸安排的協定。借款人為一定數量的現金向出借人發行債券，債券即是借款人的「借據」。這種約定使發行人有義務在既定日期向債券持有者支付指定數額款項。典型的附息債券的發行人在債券存續期內有義務每半年向債券持有者支付一次利息。在計算機出現之前，大多數的債券都有息票，投資者剪下息票並拿到發行人處索取利息收益，故被稱為息票支付。當債券到期時，發行人會支付債券的面值(par value,or face value)來清償債務。債券的票面利率(couponrte)決定了所需支付的利息：年支付額等於債券的票面利率乘以債券面值。票面利率、到期日以及債券面值均是債券契約(bond indenture)的組成部分，債券契約則是發行人與債權人之間的合約。

零息票債權不給利息，而是採用低於票面價值發售來讓購買者賺取面值之差。

模型【14-1】：債權價值

\[P_B=\frac{c}{1+r} +\frac{c}{(1+r)^2}+\dots +\frac{c+p}{(1+r)^n} \]

或

\[P_B=\sum_{t=1}^{T}\frac{c}{(1+r)^t} +\frac{c+p}{(1+r)^T} \]

根據等比數列的計算方法

模型【14-2】：債權價值

\[P=\frac{c}{r}[1-\frac{1}{(1+r)^T}]+\frac{FV}{(1+r)^T} \]

作為還沒被售賣的債權，發行方往往會根據債權的價值來決定債權的價格，於是

我們可以來探究債權價格與收益率的關係

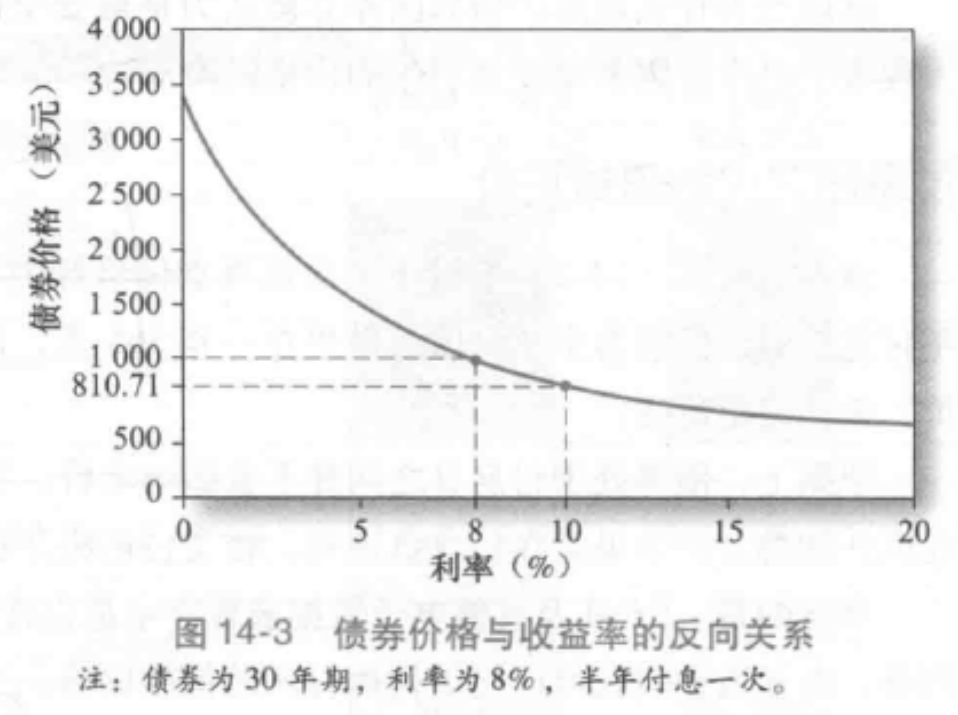
從圖14-3中曲線的形狀可以觀察到利率的上升導致的價格下跌的幅度要小於相同程度的利率下降導致的價格上升的幅度。債券價格的這一特性被稱為凸性(convexity)。

債券發行之後，債權人將在二級市場買賣債券。在各類市場中，債券價格與市場利率呈反向變動。

對溢價債券(premium bond)而言（債券以高於面值的價格出售），票面利率高於當期收益率，當期收益率高於到期收益率；對摺價債券(discount bond)而言（債券以低於面值的價格出售)，上述概念正好相反。

第十六章：債券資產組合管理

因為利率風險對積極策略和消極策略的選擇至關重要，所以我們首先討論債券價格對利率波動的敏感性。敏感性是由債券久期來測度的，我們對債券久期的決定因素將給予特別關注。

(1)債券價格與收益成反比：當收益升高時，債券價格下跌；當收益下降時，債券價格上升。
(2)債券的到期收益率升高導致其價格變化的幅度小於同等規模的收益下降導致其價格變化的幅度。

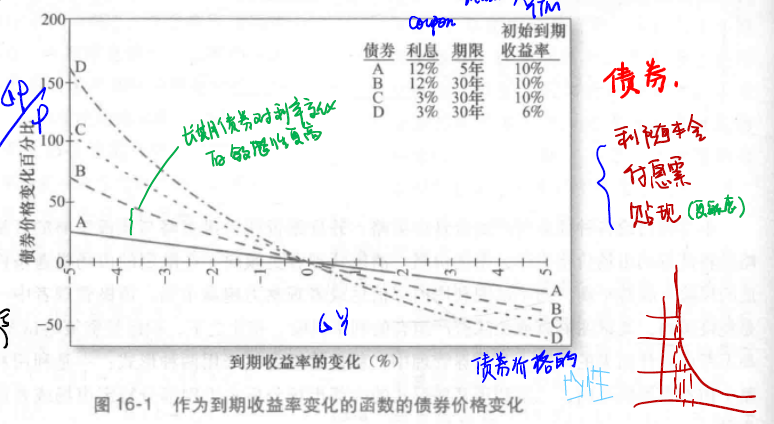
(3)長期債券價格對利率變化的敏感性比短期債券更高。

(4)當債券期限增加時，債券價格對收益率變化的敏感性增加，但增速遞減。換句話說，利率風險變動小於債券期限變動。

(5)利率風險與債券票面利率成反比。低票面利率債券的價格比高票面利率債券的價格對利率變化更敏感。

(6)債券價格對其收益變化的敏感性與當期出售債券的到期收益率成反比。

原創作者：孤飛-部落格園
原文連結：https://www.cnblogs.com/ranxi169/p/16927883.html
本文禁止任何形式的轉載！