基於Sklearn機器學習程式碼實戰
LinearRegression
線性迴歸入門
資料生成
為了直觀地看到演演算法的思路,我們先生成一些二維資料來直觀展現
import numpy as np
import matplotlib.pyplot as plt
def true_fun(X): # 這是我們設定的真實函數,即ground truth的模型
return 1.5*X + 0.2
np.random.seed(0) # 設定隨機種子
n_samples = 30 # 設定取樣資料點的個數
'''生成亂資料作為訓練集,並且加一些噪聲'''
X_train = np.sort(np.random.rand(n_samples))
y_train = (true_fun(X_train) + np.random.randn(n_samples) * 0.05).reshape(n_samples,1)
# 訓練資料是加上一定的隨機噪聲的
定義模型
我們可以直接點用sklearn中的LinearRegression即可:
from sklearn.linear_model import LinearRegression
model = LinearRegression() # 這就是我們的模型
model.fit(X_train[:, np.newaxis], y_train) # 訓練模型
print("輸出引數w:",model.coef_)
print("輸出引數b:",model.intercept_)
輸出引數w: [[1.4474774]]
輸出引數b: [0.22557542]
注意上面程式碼中的np.newaxis,因為X_train是一個一維的向量,那麼其作用就是將X_train變成一個N*1的二維矩陣而已。其實寫成X_train[:,None]是相同的效果。
至於為什麼要這麼做,你可以不這麼做試一下,會報錯為:
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
可以簡單理解為這是sklearn的庫對訓練資料的要求,不能夠是一個一維的向量。
模型測試與比較
可以看到我們輸出為1.44和0.22,還是很接近真實答案的,那麼我們選取一批測試集來看看精度:
X_test = np.linspace(0,1,100) # 0和1之間,產生100個等間距的
plt.plot(X_test, model.predict(X_test[:, np.newaxis]), label = "Model") # 將擬合出來的散點畫出
plt.plot(X_test, true_fun(X_test), label = "True function") # 真實結果
plt.scatter(X_train, y_train) # 畫出訓練集的點
plt.legend(loc="best") # 將標籤放在最合適的位置
plt.show()

上述情況是最簡單的,但當出現更高維度時,我們就需要進行多項式迴歸才能夠滿足需求了。
多項式迴歸
具體實現
對於多項式迴歸,一般是利用線性迴歸求解\(y=\sum_{i=1}^m b_i \times x^i\),因此演演算法如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures # 匯入能夠計算多項式特徵的類
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score # 交叉驗證
def true_fun(X): # 真實函數
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
X = np.sort(np.random.rand(n_samples)) # 隨機取樣後排序
y = true_fun(X) + np.random.randn(n_samples) * 0.1
degrees = [1, 4, 15] # 多項式最高次,我們分別用1次,4次和15次的多項式來嘗試擬合
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i+1) # 總共三個圖,獲取第i+1個圖的影象柄
plt.setp(ax, xticks = (), yticks = ()) # 這是 設定ax圖中的屬性
polynomial_features = PolynomialFeatures(degree=degrees[i],include_bias=False)
# 建立多項式迴歸的類,第一個引數就是多項式的最高次數,第二個是是否包含偏置
linear_regression = LinearRegression() # 線性迴歸
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)]) # 使用pipline串聯模型
pipeline.fit(X[:, np.newaxis], y)
scores = cross_val_score(pipeline, X[:, np.newaxis], y, scoring="neg_mean_squared_error", cv=10)
# 使用交叉驗證,第一個引數為模型,第二個為輸入,第三個為標籤,第四個為誤差計算方式,第五個為多少折
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="True function")
plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc="best")
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(degrees[i], -scores.mean(), scores.std()))
plt.show()

這裡解釋兩個地方:
- PolynomialFeatures:這個類實際上是一個構造特徵的類,因為我們原始的X是一個一維的向量,它多項式的次數為1,那我們希望構成一個多項式就需要拿X去計算\(X^1,X^2,...,X^m\)(這是一個變數的情況,如果是多個變數就會計算交叉乘),那麼這個類就是實現這樣的操作,構造成m個特徵
- pipeline:這是方便我們的管道,它將各種模組加在一起讓我們不用一步步去計算每一個模組,這裡就是將PolynomialFeatures和線性迴歸模組加在一起,那我們將X傳進去之後,就經過特徵構造後就進行線性迴歸,因此擬合管道即可。
在其中我們還用到了交叉驗證的思路,這部分很常見就不多做解釋了。
LogisticRegression
演演算法思想簡述
對於邏輯迴歸大部分是面對二分類問題,給定資料\(X=\{x_1,x_2,...,\},Y=\{y_1,y_2,...,\}\)
考慮二分類任務,那麼其假設函數就是:
來表示為類別1或者類別0的概率。
那麼其損失函數一般是採用極大似然估計法來定義:
這裡假設\(y_1=1,y_2=0\)。那麼就是該函數最大化,化簡可得:
再利用梯度下降即可。
演演算法實現
# 下面為sklearn版本
import numpy as np
from sklearn.datasets import fetch_openml
mnist = fetch_openml("mnist_784") # 資料
X, y = mnist['data'], mnist['target']
X_train = np.array(X[:60000], dtype = float)
y_train = np.array(y[:60000], dtype = float)
X_test = np.array(X[60000:], dtype = float)
y_test = np.array(y[60000:], dtype = float) # 構造訓練集和資料集
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
(60000, 784)
(60000,)
(10000, 784)
(10000,)
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(penalty='l1', solver='saga', tol=0.1)
# 第一個引數為懲罰項選擇l1還是l2,tol是停止求解的條件,solver可以認為是求解器
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print("Test score with L1 penalty: %.4f" % score)
Test score with L1 penalty: 0.9245
這裡我好奇的是邏輯迴歸面對的是二分類問題,可是這裡我們直接給他多分類問題的資料集為何能夠直接求解,查了一遍發現是類內部的優化幫你實現了這一過程。
# 以下為pytorch版本
from torch.utils.data import DataLoader
from torchvision import datasets
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
import numpy as np
train_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = True,transform = transforms.ToTensor(), download = False)
test_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = False, transform = transforms.ToTensor(), download = False)
#載入資料集
batch_size = len(train_dataset)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True)
# 資料載入器
X_train,y_train = next(iter(train_loader))
X_test,y_test = next(iter(test_loader))
# 列印前100張圖片
images, labels= X_train[:100], y_train[:100]
# 使用images生成寬度為10張圖的網格大小
img = torchvision.utils.make_grid(images, nrow=10)
# cv2.imshow()的格式是(size1,size1,channels),而img的格式是(channels,size1,size1),
# 所以需要使用.transpose()轉換,將顏色通道數放至第三維
img = img.numpy().transpose(1,2,0)
print(images.shape)
print(labels.reshape(10,10))
print(img.shape)
plt.imshow(img)
plt.show()
torch.Size([100, 1, 28, 28])
tensor([[4, 7, 0, 9, 3, 6, 1, 7, 7, 8],
[8, 3, 2, 7, 2, 4, 4, 3, 8, 0],
[5, 6, 4, 9, 0, 6, 1, 2, 3, 3],
[6, 0, 4, 3, 7, 0, 7, 6, 5, 1],
[4, 3, 4, 8, 5, 3, 1, 5, 2, 4],
[5, 4, 8, 5, 5, 1, 1, 6, 0, 4],
[5, 4, 5, 1, 4, 4, 8, 2, 7, 3],
[8, 1, 8, 6, 3, 7, 7, 9, 5, 9],
[8, 4, 7, 0, 3, 6, 6, 2, 5, 3],
[2, 0, 6, 5, 1, 7, 2, 7, 1, 2]])
(302, 302, 3)

X_train,y_train = X_train.cpu().numpy(),y_train.cpu().numpy() # tensor轉為array形式)
X_test,y_test = X_test.cpu().numpy(),y_test.cpu().numpy() # tensor轉為array形式)
X_train = X_train.reshape(X_train.shape[0],784) # 展開成1維度的向量的形式,長度為28*28等於784
X_test = X_test.reshape(X_test.shape[0],784)
model = LogisticRegression(solver='lbfgs', max_iter = 400)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(classification_report(y_test, y_pred)) # 列印報告
precision recall f1-score support
0 0.50 0.75 0.60 4
1 0.71 1.00 0.83 10
2 0.79 0.85 0.81 13
3 0.79 0.69 0.73 16
4 0.83 0.91 0.87 11
5 0.60 0.23 0.33 13
6 1.00 1.00 1.00 5
7 0.88 1.00 0.93 7
8 0.67 0.83 0.74 12
9 0.71 0.56 0.63 9
accuracy 0.75 100
macro avg 0.75 0.78 0.75 100
weighted avg 0.74 0.75 0.73 100
Decision Tree
首先介紹一個資料集,鳶尾花(iris)資料集,資料集內包含 3 類共 150 條記錄,每類各 50 個資料,每條記錄都有 4 項特徵:花萼長度、花萼寬度、花瓣長度、花瓣寬度,可以通過這4個特徵預測鳶尾花卉屬於(iris-setosa, iris-versicolour, iris-virginica)中的哪一品種。
import seaborn as sns
from pandas import plotting
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import tree
# 載入資料集
data = load_iris()
# 轉換成DataFrame的格式
df = pd.DataFrame(data.data, columns=data.feature_names)
df['Species'] = data.target # 新增品種列
# 檢視資料集資訊
print(f"資料集資訊:\n{df.info()}")
# 檢視前5條資料
print(f"前5條資料:\n{df.head()}")
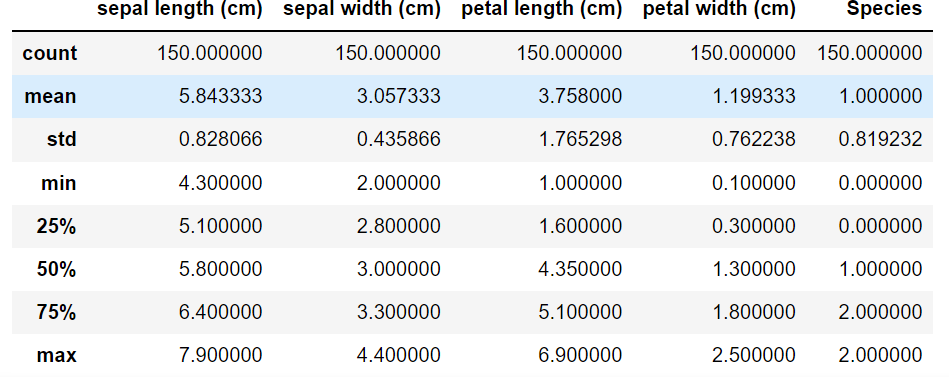
df.describe()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal length (cm) 150 non-null float64
1 sepal width (cm) 150 non-null float64
2 petal length (cm) 150 non-null float64
3 petal width (cm) 150 non-null float64
4 Species 150 non-null int32
dtypes: float64(4), int32(1)
memory usage: 5.4 KB
資料集資訊:
None
前5條資料:
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
Species
0 0
1 0
2 0
3 0
4 0
上述是對資料的初步觀察,下面來看具體的演演算法實現:
# 用數值代替品類名稱
target = np.unique(data.target) # 去重
print(target)
target_names = np.unique(data.target_names)
print(target_names)
targets = dict(zip(target, target_names))
print(targets)
df['Species'] = df['Species'].replace(targets)
# 提取資料和標籤
X =df.drop(columns = 'Species') # 把標籤列丟掉就是特徵
y = df['Species']
feature_names = X.columns
labels = y.unique()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state=42)
# 劃分訓練集與測試集,測試集比例為0.4,隨機種子為42
model = DecisionTreeClassifier(max_depth = 3, random_state = 42) # 決策樹的最大深度為3
model.fit(X_train, y_train)
# 以文字的形式輸出樹
text_representation = tree.export_text(model)
print(text_representation)
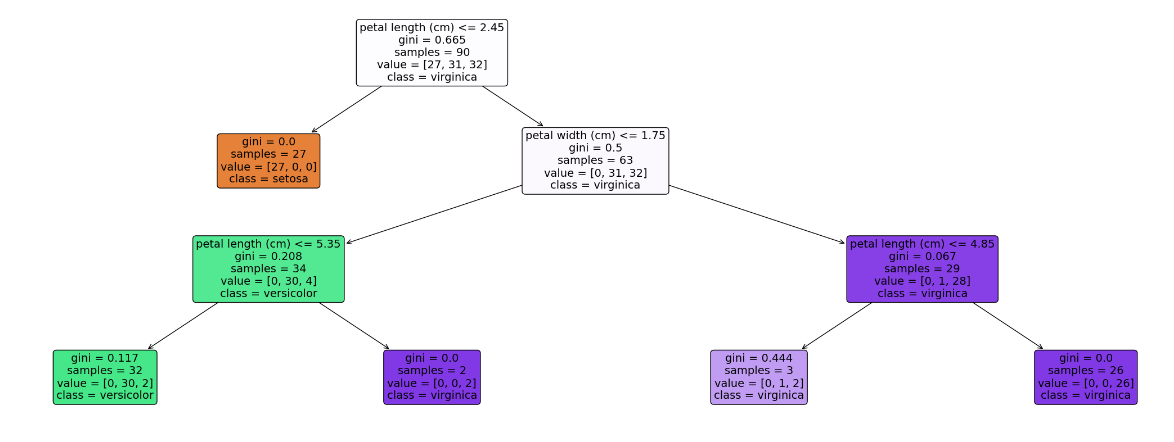
# 以圖片的形式畫出
plt.figure(figsize=(30, 10), facecolor='w')
a = tree.plot_tree(model,
feature_names = feature_names,
class_names = labels,
rounded = True,
filled = True,
fontsize = 14)
plt.show()
[0 1 2]
['setosa' 'versicolor' 'virginica']
{0: 'setosa', 1: 'versicolor', 2: 'virginica'}
|--- feature_2 <= 2.45
| |--- class: setosa
|--- feature_2 > 2.45
| |--- feature_3 <= 1.75
| | |--- feature_2 <= 5.35
| | | |--- class: versicolor
| | |--- feature_2 > 5.35
| | | |--- class: virginica
| |--- feature_3 > 1.75
| | |--- feature_2 <= 4.85
| | | |--- class: virginica
| | |--- feature_2 > 4.85
| | | |--- class: virginica
MLP
多層感知機的介紹可以看我這篇講神經網路的部落格
下面我們關注演演算法實現
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import fetch_openml
import numpy as np
mnist = fetch_openml("mnist_784") # 載入資料集
X, y = mnist['data'], mnist['target']
X_train = np.array(X[:60000], dtype=float)
y_train = np.array(y[:60000], dtype=float)
X_test = np.array(X[60000:], dtype=float)
y_test = np.array(y[60000:], dtype=float)
clf = MLPClassifier(alpha = 1e-5, hidden_layer_sizes = (15,15), random_state=1)
# alpha為正則項的懲罰係數,第二個為每一層隱藏節點的個數,這裡就是2層,每層15個
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
score
0.9124
那麼還有一些值得注意的引數為:
- activation:選擇啟用函數,可選有{'identity','logistic','tanh','relu'},預設為relu
- solver:權重優化器,可選有{'lbfgs','sgd','adam'},預設為adam
- learning_rate_init:初始學習率,僅在sgd或者adam時使用
SVM
我們還是專注於SVM演演算法的實現。
選擇不同的核主要是在svm.SVC中指定引數kernel
線性SVM
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
data = np.array([
[0.1, 0.7],
[0.3, 0.6],
[0.4, 0.1],
[0.5, 0.4],
[0.8, 0.04],
[0.42, 0.6],
[0.9, 0.4],
[0.6, 0.5],
[0.7, 0.2],
[0.7, 0.67],
[0.27, 0.8],
[0.5, 0.72]
])# 建立資料集
label = [1] * 6 + [0] * 6 # 前6個資料的label為1,後6個為0
x_min, x_max = data[:,0].min() - 0.2, data[:,0].max() + 0.2
y_min, y_max = data[:,1].min() - 0.2, data[:,0].max() + 0.2
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.002),
np.arange(y_min, y_max, 0.002)) # 生成網格網路
model_linear = svm.SVC(kernel = 'linear', C = 0.001) # 線性SVM模型
model_linear.fit(data, label)
Z = model_linear.predict(np.c_[xx.ravel(), yy.ravel()])
# 是先將xx(size*size)和yy(size*size)拉成一維,然後讓它們相連,成為一個兩列的矩陣,然後作為X進去預測
Z = Z.reshape(xx.shape)
plt.contourf(xx,yy, Z, cmap=plt.cm.ocean, alpha=0.6)
# 可以理解為繪製等高線,xx為橫座標,yy為軸座標,Z為確切座標點的取值,cmap為配色方案
plt.scatter(data[:6,0],data[:6,1], marker='o', color='r', s=100, lw=3)
plt.scatter(data[6:,0],data[6:,1], marker='x', color='k', s=100, lw=3)
plt.title("Linear SVM")
plt.show()

多項式核
plt.figure(figsize=(16,15))
# 畫出多個多項式等級來對比
for i, degree in enumerate([1,3,5,7,9,12]):
model_poly = svm.SVC(C=0.001, kernel='poly', degree = degree) # 多項式核
model_poly.fit(data, label)
Z = model_poly.predict(np.c_[xx.ravel(), yy.ravel()])#預測
Z = Z.reshape(xx.shape)
plt.subplot(3,2, i+1)
plt.subplots_adjust(wspace=0.2, hspace=0.2) # 調整子圖的間距
plt.contourf(xx,yy, Z, cmap=plt.cm.ocean, alpha=0.6)
plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
plt.title('Poly SVM with $\degree=$' + str(degree))
plt.show()

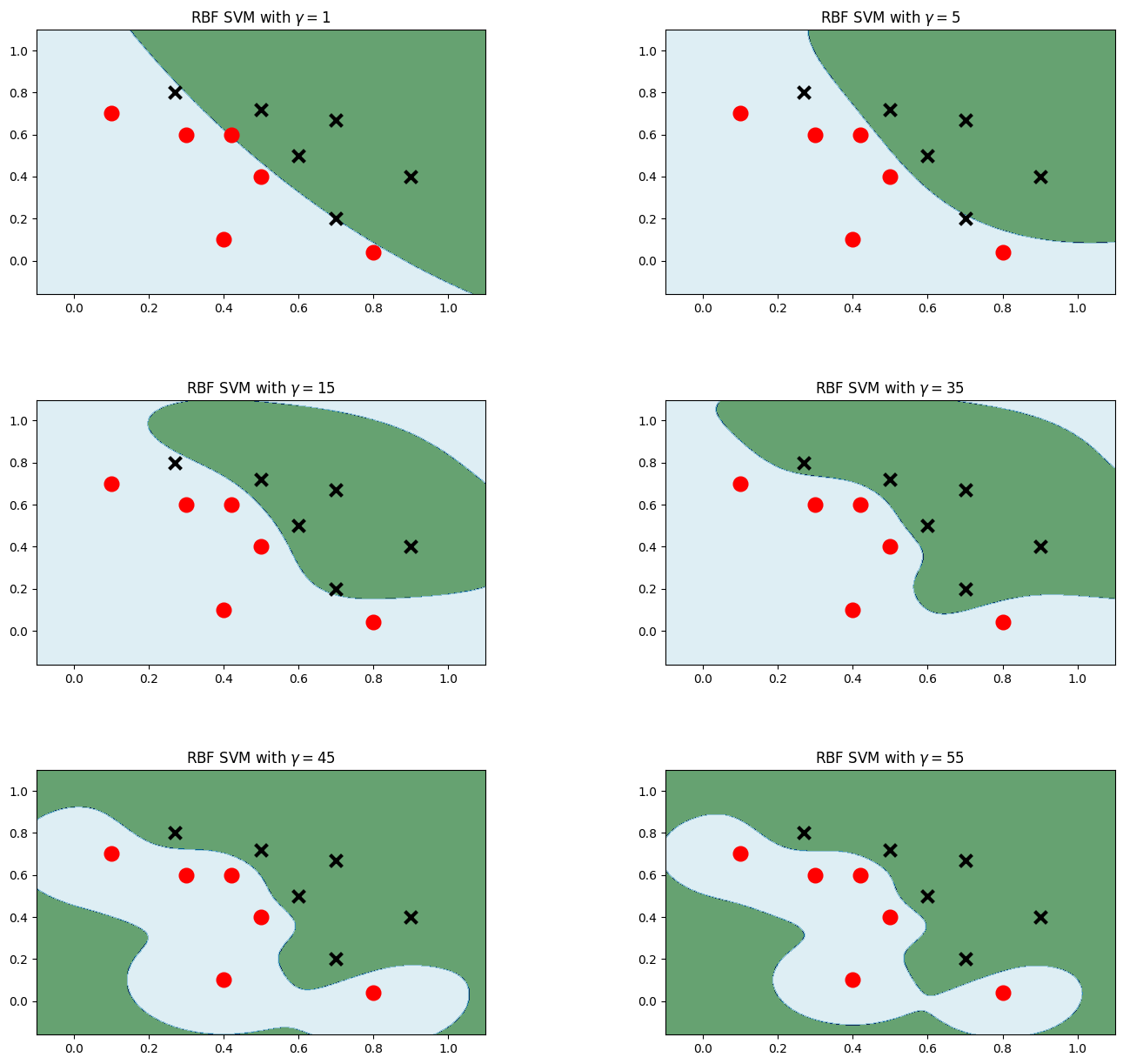
高斯核
plt.figure(figsize=(16,15))
for i, gamma in enumerate([1,5,15,35,45,55]):
model_rbf = svm.SVC(kernel='rbf', gamma=gamma, C = 0.001) # 選擇高斯核模型
model_rbf.fit(data, label)
Z = model_rbf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.subplot(3, 2, i + 1)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)
# 畫出訓練點
plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
plt.title('RBF SVM with $\gamma=$' + str(gamma))
plt.show()
對比不同核在Mnist上的效果
讀取資料
from sklearn import svm
import numpy as np
from time import time
from sklearn.metrics import accuracy_score
from struct import unpack
from sklearn.model_selection import GridSearchCV
def readimage(path):
with open(path, 'rb') as f:
magic, num, rows, cols = unpack('>4I', f.read(16))
img = np.fromfile(f, dtype=np.uint8).reshape(num, 784)
return img
def readlabel(path):
with open(path, 'rb') as f:
magic, num = unpack('>2I', f.read(8))
lab = np.fromfile(f, dtype=np.uint8)
return lab
train_data = readimage("../../datasets/MNIST/raw/train-images-idx3-ubyte")#讀取資料
train_label = readlabel("../../datasets/MNIST/raw/train-labels-idx1-ubyte")
test_data = readimage("../../datasets/MNIST/raw/t10k-images-idx3-ubyte")
test_label = readlabel("../../datasets/MNIST/raw/t10k-labels-idx1-ubyte")
print(train_data.shape)
print(train_label.shape)
(60000, 784)
(60000,)
高斯核
#資料集中資料太多,為了節約時間,我們只使用前4000張進行訓練
train_data=train_data[:4000]
train_label=train_label[:4000]
test_data=test_data[:400]
test_label=test_label[:400]
svc=svm.SVC()
parameters = {"kernel":['rbf'], "C":[1]}
print("Train....")
clf = GridSearchCV(svc, parameters, n_jobs=-1) # 網格搜尋來決定引數
start = time()
clf.fit(train_data, train_label)
end = time()
t = end - start
print("訓練時間:%dmin%.3fsec" % (t//60, t-60 * (t//60)))
prediction = clf.predict(test_data)
print("accuracy:",accuracy_score(prediction, test_label))
accurate = [0] * 10
sumall = [0] * 10
i = 0
j = 0
while i < len(test_label):
sumall[test_label[i]] += 1
if prediction[i] == test_label[i]:
j += 1
i += 1
print("測試集準確率:", j/400)
Train....
訓練時間:0min7.548sec
accuracy: 0.955
測試集準確率: 0.955
多項式核
parameters = {'kernel':['poly'], 'C':[1]}#使用了多項式核
print("Train...")
clf=GridSearchCV(svc,parameters,n_jobs=-1)
start = time()
clf.fit(train_data, train_label)
end = time()
t = end - start
print('Train:%dmin%.3fsec' % (t//60, t - 60 * (t//60)))
prediction = clf.predict(test_data)
print("accuracy: ", accuracy_score(prediction, test_label))
accurate=[0]*10
sumall=[0]*10
i=0
j=0
while i<len(test_label):#計算測試集的準確率
sumall[test_label[i]]+=1
if prediction[i]==test_label[i]:
j+=1
i+=1
print("測試集準確率:",j/400)
Train...
Train:0min6.438sec
accuracy: 0.93
測試集準確率: 0.93
線性核
parameters = {'kernel':['linear'], 'C':[1]}#使用了線性核
print("Train...")
clf=GridSearchCV(svc,parameters,n_jobs=-1)
start = time()
clf.fit(train_data, train_label)
end = time()
t = end - start
print('Train:%dmin%.3fsec' % (t//60, t - 60 * (t//60)))
prediction = clf.predict(test_data)
print("accuracy: ", accuracy_score(prediction, test_label))
accurate=[0]*10
sumall=[0]*10
i=0
j=0
while i<len(test_label):#計算測試集的準確率
sumall[test_label[i]]+=1
if prediction[i]==test_label[i]:
j+=1
i+=1
print("測試集準確率:",j/400)
Train...
Train:0min3.712sec
accuracy: 0.9175
測試集準確率: 0.9175
NBayes
這部分演演算法的呼叫相對簡單:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
from sklearn.datasets import make_blobs
# make_blobs:為聚類產生資料集
# n_samples:樣本點數,n_features:資料的維度,centers:產生資料的中心點,預設值3
# cluster_std:資料集的標準差,浮點數或者浮點數序列,預設值1.0,random_state:隨機種子
X, y = make_blobs(n_samples = 100, n_features = 2, centers = 2, random_state = 2, cluster_std = 1.5)
plt.scatter(X[:,0], X[:,1], c = y, s = 50, cmap = 'RdBu')
plt.show()
先畫出訓練集的散點圖:
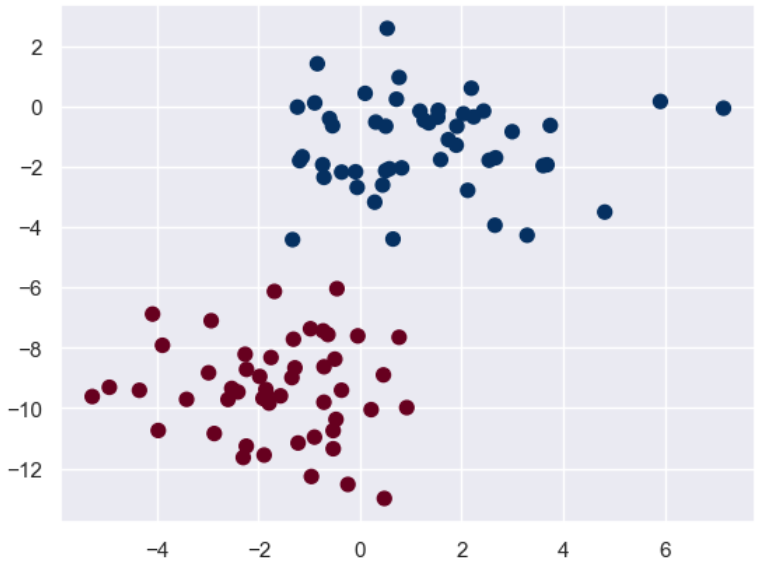
接下來我們再構建自己的測試集來看看效果:
from sklearn.naive_bayes import GaussianNB
model = GaussianNB() # 樸素貝葉斯
model.fit(X, y)
rng = np.random.RandomState(0)
X_test = [-6, -14] + [14,18] * rng.rand(5000,2) # 生成測試集
y_pred = model.predict(X_test)
# 將訓練集和測試集的資料用影象表示出來,顏色深直徑大的為訓練集,顏色淺直徑小的為測試集
plt.scatter(X[:,0],X[:,1], c = y, s = 50, cmap = 'RdBu')
lim = plt.axis() # 獲取當前的座標軸限制引數
plt.scatter(X_test[:,0], X_test[:,1], c = y_pred, s = 20, cmap='RdBu', alpha = 0.1)
plt.axis(lim)
plt.show()

可以看到基本上兩個分類的邊界還是很明顯的。
我們也可以看看預測出來的概率大概是什麼樣子:
yprob = model.predict_proba(X_test)
yprob[:20].round(2)
Out[25]:
array([[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[1. , 0. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0. , 1. ],
[0.94, 0.06],
[0. , 1. ],
[0. , 1. ],
[0.01, 0.99],
[0. , 1. ],
[0. , 1. ]])
bagging與隨機森林
關於這方面的介紹可以看我這篇部落格。
下面我們繼續關注演演算法的實現:
首先是資料集的載入:
import pandas as pd
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
wine = load_wine() # 使用葡萄酒資料集
print(f"所有特徵:{wine.feature_names}")
X = pd.DataFrame(wine.data, columns = wine.feature_names)
y = pd.Series(wine.target)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 1)
所有特徵:['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
接下來我們簡單看看如果用單個的決策樹將會有什麼樣的結果:
# 構造並訓練決策樹分類器
base_model = DecisionTreeClassifier(max_depth = 1, criterion='gini', random_state = 1)
# 使用基尼指數作為選擇標準
base_model.fit(X_train, y_train)
y_pred = base_model.predict(X_test)
print(f"決策樹的準確率為:{accuracy_score(y_test, y_pred):.3f}")
決策樹的準確率為:0.694
可以看到,對於簡單的決策樹來說其精確度並不夠。
那麼我們嘗試一下以該決策樹作為基分類器的bagging整合,看看能有多大的提升:
from sklearn.ensemble import BaggingClassifier
# 這裡的基分類器選擇是上面構建的決策樹模型,前面雖然已經fit了一次,但是不影響,應該也是重新fit的
model = BaggingClassifier(base_estimator = base_model,
n_estimators = 50, # 最大的弱學習器的個數為50
random_state = 1)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)# 預測
print(f"BaggingClassifier的準確率:{accuracy_score(y_test,y_pred):.3f}")
BaggingClassifier的準確率:0.917
可以看到提升還是很明顯的!接下來我們關注一下重要引數——基分類器的個數對結果的影響:
# 下面來測試基分類器個數的影響
x = list(range(2,102,2)) # 從2到102之間的偶數
y = []
for i in x:
model = BaggingClassifier(base_estimator = base_model,
n_estimators = i,
random_state = 1)
model.fit(X_train, y_train)
model_test_sc = accuracy_score(y_test, model.predict(X_test))
y.append(model_test_sc) # 將得分進行儲存
plt.style.use('ggplot') # 設定繪圖背景樣式
plt.title("Effect of n_estimators", pad = 20)
plt.xlabel("Number of base estimators")
plt.ylabel("Test accuracy of BaggingClassifier")
plt.plot(x,y)
plt.show()

可以看到基分類器的數量並不是越多越好的!這是因為太多可能會出現冗餘,導致分類結果不好。
接下來來觀察改進演演算法——隨機森林的實現:
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier( n_estimators = 50,
random_state = 1)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"RandomForestClassifier的準確率:{accuracy_score(y_test,y_pred):.3f}")
RandomForestClassifier的準確率:0.972
可以看到隨機森林因為加入了特徵隨機性,因此其基分類器的多樣性得到提升,進而分類精度也就得到進一步的提升。
我們也來觀察基分類器個數對結果的影響:
x = list(range(2, 102, 2))# 估計器個數即n_estimators,在這裡我們取[2,102]的偶數
y = []
for i in x:
model = RandomForestClassifier(
n_estimators=i,
random_state=1)
model.fit(X_train, y_train)
model_test_sc = accuracy_score(y_test, model.predict(X_test))
y.append(model_test_sc)
plt.style.use('ggplot')
plt.title("Effect of n_estimators", pad=20)
plt.xlabel("Number of base estimators")
plt.ylabel("Test accuracy of RandomForestClassifier")
plt.plot(x, y)
plt.show()

可以看對對於隨機森林來說,我覺得是因為它加入了特徵的隨機性,因此對於數量就不那麼敏感。
AdaBoost
關於AdaBoost的介紹也可以看我這篇部落格。
下面我們仍然關注演演算法的實現:
同樣先匯入資料,然後看看在單個決策樹上的模型好壞:
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn import metrics
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
wine = load_wine()#使用葡萄酒資料集
print(f"所有特徵:{wine.feature_names}")
X = pd.DataFrame(wine.data, columns=wine.feature_names)
y = pd.Series(wine.target)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=1)
base_model = DecisionTreeClassifier(max_depth = 1, criterion='gini', random_state = 1)
base_model.fit(X_train, y_train)
y_pred = base_model.predict(X_test)
print(f"決策樹的準確率:{accuracy_score(y_test,y_pred):.3f}")
決策樹的準確率:0.694
跟之前的結果是一樣的。
那麼接下來我們嘗試應用AdaBoost演演算法來擬合:
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import GridSearchCV
model = AdaBoostClassifier(base_estimator=base_model, n_estimators=50, learning_rate = 0.8)
# n_estimators和learning_rate是要調的引數,lr是弱學習器的權重衰減係數
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
acc = metrics.accuracy_score(y_test, y_pred) # 準確率
print(f"準確率:{acc:.2}")
準確率:0.97
可以看到其效果提升很多!但是這個引數是我們隨機初始化的,我們嘗試用網格搜尋來搜尋在訓練集上表現最佳的引數:
hyperparameter_space = {"n_estimators":list(range(2,102,2)),
"learning_rate":[0,1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1]}
gs = GridSearchCV(AdaBoostClassifier(algorithm='SAMME.R', random_state = 1),
param_grid = hyperparameter_space,
scoring = 'accuracy', n_jobs = -1, cv = 5)
gs.fit(X_train, y_train)
print("最佳引數為:",gs.best_params_)
print("最佳得分為:",gs.best_score_)
最佳引數為: {'learning_rate': 0.8, 'n_estimators': 42}
最佳得分為:0.9857142857142858
再看看它在測試集上的分數:
model = AdaBoostClassifier(base_estimator=base_model, n_estimators=42, learning_rate = 0.8)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
acc = metrics.accuracy_score(y_test, y_pred) # 準確率
print(f"準確率:{acc:.2}")
準確率:0.94
可以看到居然還不如我們之前的引數。這裡要注意在進行網格搜尋的時候就進行了K折交叉驗證的。我一開始是以為網格搜尋是在訓練集上尋找擬合效果最好的引數,這點需要注意。
k-means演演算法
關於聚類演演算法的詳細介紹可以看我這篇部落格。
下面我們繼續關注演演算法實現。
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
from sklearn import datasets
%matplotlib inline
# 聚類前
X = np.random.rand(1000,2)
plt.scatter(X[:,0], X[:,1], marker='o')

# 初始化質心,從原有資料中挑選k個作為質心
def IiniCentroids(X, k):
index = np.random.randint(0, len(X)-1, k)
return X[index]
# 聚類後
kmeans = KMeans(n_clusters = 4) # 分成2類
kmeans.fit(X)
label_pred = kmeans.labels_
plt.scatter(X[:,0], X[:,1], c= label_pred)
plt.show()

他給的程式碼比較少,因此我去搜尋了該函數的其他引數:
- n_clusters:int型別,生成的聚類數,預設為8
- max_iter:int型別,執行最大迭代次數,預設為300
- n_init:選擇多份不同的聚類中心,同樣執行結果最終選取一個
- init:有三個可選值
- k-means++:預設,用特殊方法選定初始質心並加速收斂
- random:隨機從訓練資料中選取質心
- 傳遞一個ndarray:自己指定質心
- n_jobs
- random_state
它的主要屬性有:
- cluster_centers_:最後的聚類中心
- labels:每個樣本對應的簇
- inertia_:用來評估簇的個數是否合適,距離越小說明分得越好,用來選擇簇最佳個數
print("聚類中心為:",kmeans.cluster_centers_)
print("評估:",kmeans.inertia_)
聚類中心為: [[0.79862048 0.71591318]
[0.22582347 0.26005466]
[0.73845863 0.23886344]
[0.29972473 0.76998545]]
評估: 41.37635968102986
KNN
這個演演算法的介紹可以看我這篇部落格,裡面講解了演演算法以及詳細的python實現過程。
下面我們專注於利用sklearn的實現過程。
sklearn 庫的 neighbors 模組實現了KNN 相關演演算法,其中:
- KNeighborsClassifier類用於實現分類問題
- KNeighborsRegressor類用於實現迴歸問題(迴歸問題簡單理解就是附近點在特徵上的平均值賦給目標點)
這兩個類的構造方法基本一致,這裡我們主要介紹 KNeighborsClassifier 類,原型如下:
KNeighborsClassifier(
n_neighbors=5,
weights='uniform',
algorithm='auto',
leaf_size=30,
p=2,
metric='minkowski',
metric_params=None,
n_jobs=None,
**kwargs)
主要關注這幾個引數:
- n_neighbors:即 KNN 中的 K 值,一般使用預設值 5。
- weights:用於確定鄰居的權重,有三種方式:
- weights=uniform,表示所有鄰居的權重相同
- weights=distance,表示權重是距離的倒數,即與距離成反比
- 自定義函數,可以自定義不同距離所對應的權重,一般不需要自己定義函數
- algorithm:用於設定計算鄰居的演演算法,它有四種方式:
- algorithm=auto,根據資料的情況自動選擇適合的演演算法
- algorithm=kd_tree,使用 KD 樹演演算法
- KD 樹適用於維度較少的情況,一般維數不超過 20,如果維數大於 20 之後,效率會下降
- algorithm=ball_tree,使用球樹演演算法
- 球樹更適用於維度較大的情況
- algorithm=brute,稱為暴力搜尋
- 它和 KD 樹相比,採用的是線性掃描,而不是通過構造樹結構進行快速檢索
- 缺點是,當訓練集較大的時候,效率很低
- leaf_size:表示構造 KD 樹或球樹時的葉子節點數,預設是 30
下面來進入程式碼實戰:
from sklearn.datasets import load_digits
import pandas as pd
digits = load_digits()
data = digits.data # 特徵集
target = digits.target # 目標集
data_pd = pd.DataFrame(data)
data_pd
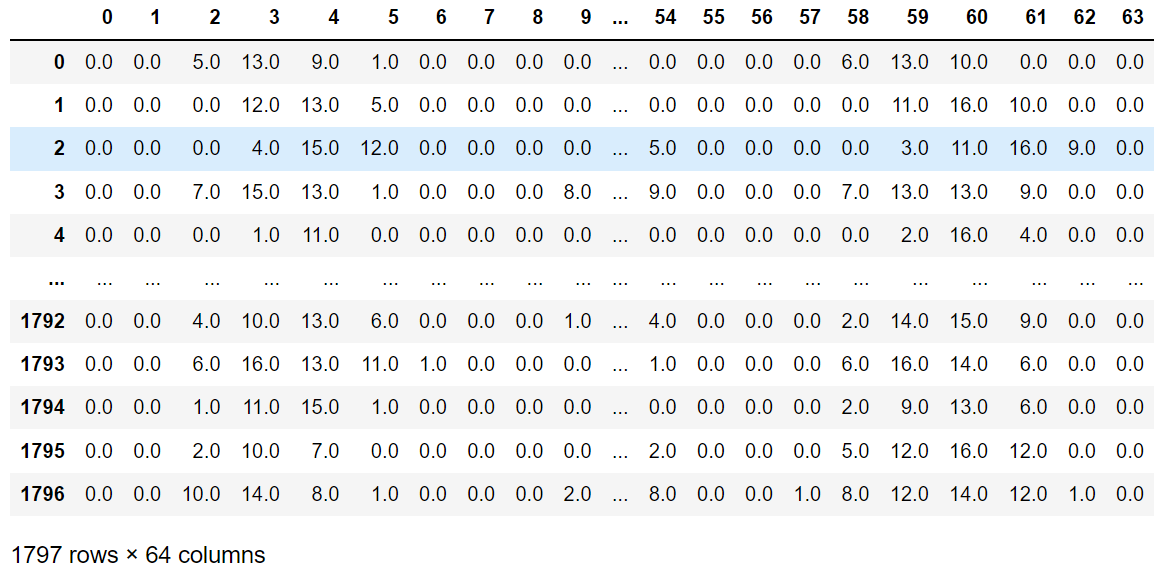
可以看到是64個維度,相當於是一個64維空間下的一個散點。
from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(
data, target, test_size=0.25, random_state=33)
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(train_x, train_y)
predict_y = knn.predict(test_x)
from sklearn.metrics import accuracy_score
score = accuracy_score(test_y, predict_y)
score
0.9844444444444445
PCA
關於PCA演演算法的詳細解釋可以看我這篇部落格,講解了PCA演演算法以及Numpy實現PCA的過程。
下面我們繼續關注演演算法的實現過程:
#首先我們生成亂資料並視覺化
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
from sklearn.datasets import make_blobs
# X為樣本特徵,Y為樣本簇類別, 共1000個樣本,每個樣本3個特徵,共4個簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]],
cluster_std=[0.2, 0.1, 0.2, 0.2], random_state =9)
fig = plt.figure()
ax = Axes3D(fig, rect=[0,0,1,1], elev = 20, azim = 10)
# rect是左,底部,寬度,高度,用來確定範圍,elev是上下觀察視角,azim是左右觀察視角
plt.scatter(X[:,0],X[:,1], X[:,2], marker='o')

因為PCA降維的時候需要重點關注保留的方差,因此我們先不進行降維,只對資料進行投影,看看投影后的三個維度的方差分佈:
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(X)
print(pca.explained_variance_ratio_) # 各個特徵保留的方差百分比
print(pca.explained_variance_) # 各個特徵的方差原始數值
[0.98318212 0.00850037 0.00831751]
[3.78521638 0.03272613 0.03202212]
可以看到第一個維度的方差佔據了98%。
那麼接下來嘗試降到2維度:
pca = PCA(n_components=2)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
[0.98318212 0.00850037]
[3.78521638 0.03272613]
可以看到如果保留兩個維度的話,它選擇了前兩個方差佔據比較大的特徵,捨棄了第三個特徵。
我們將降維後的圖畫出來:
X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o')
plt.show()

我們剛才的降維是指定保留維度數,那我們也可以指定保留的方差比例大小:
pca = PCA(n_components=0.95)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)
[0.98318212]
[3.78521638]
1
可以看到因為第一個就佔據了98%,所以保留95%就直接保留第一個維度就可以了。
我們還可以讓MLE演演算法自己選擇降維的結果:
pca = PCA(n_components='mle')
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)
[0.98318212]
[3.78521638]
1
可以看到MLE演演算法就只保留了第一個特徵。
我們這裡補充一下該類的具體引數:
- n_components:就是指定降維後的特殊數目或者指定保留的方差比例,還可以通過設為MLE來自動選擇
- copy:布林值,是否需要將原始訓練資料複製
- whliten:布林值,是否白化,使得每個特徵都具有相同的方差
該類的屬性有:
- n_components_:返回所保留的特徵個數
- explained_variance_ratio_:返回所保留的各個特徵的方差百分比
- explained_variance_:返回所保留的各個特徵的方差大小
常用方法為:
- fit_transform(X):訓練並返回降維後的資料
- inverse_transform(newData) :將降維得到的資料newData轉換回原始資料,可能會有一點不同
- transform(X):將X轉換為降維後的資料
嘗試一下復原降維的資料:
new_Data = pca.transform(X)
X_regan = pca.inverse_transform(new_Data)
X-X_regan
array([[ 0.14364008, -0.1352249 , -0.00781994],
[ 0.05135552, -0.01316744, -0.03802959],
[-0.03610653, 0.07254754, -0.03665018],
...,
[ 0.18537785, -0.0907325 , -0.09400653],
[-0.2618617 , 0.20035984, 0.06048799],
[-0.02015389, 0.12283753, -0.10292754]])
還是有很大差距的。
HMM
對於HMM的原理介紹強烈推薦看這個視訊,真的講得很好!
我們繼續關注程式的實現。
hmmlearn實現了三種HMM模型類,按照觀測狀態是連續狀態還是離散狀態,可以分為兩類。GaussianHMM和GMMHMM是連續觀測狀態的HMM模型,而MultinomialHMM是離散觀測狀態的模型。那我們來嘗試使用一下:
#pip install hmmlearn
import numpy as np
import matplotlib.pyplot as plt
from hmmlearn import hmm
# Prepare parameters for a 4-components HMM
# Initial population probability
startprob = np.array([0.6, 0.3, 0.1, 0.0])
# The transition matrix, note that there are no transitions possible
# between component 1 and 3
transmat = np.array([[0.7, 0.2, 0.0, 0.1],
[0.3, 0.5, 0.2, 0.0],
[0.0, 0.3, 0.5, 0.2],
[0.2, 0.0, 0.2, 0.6]])
# The means of each component
means = np.array([[0.0, 0.0],
[0.0, 11.0],
[9.0, 10.0],
[11.0, -1.0]])
# The covariance of each component
covars = .5 * np.tile(np.identity(2), (4, 1, 1))
# Build an HMM instance and set parameters
gen_model = hmm.GaussianHMM(n_components=4, covariance_type="full")
# Instead of fitting it from the data, we directly set the estimated
# parameters, the means and covariance of the components
gen_model.startprob_ = startprob
gen_model.transmat_ = transmat
gen_model.means_ = means
gen_model.covars_ = covars
# Generate samples
X, Z = gen_model.sample(500)
# Plot the sampled data
fig, ax = plt.subplots()
ax.plot(X[:, 0], X[:, 1], ".-", label="observations", ms=6,
mfc="orange", alpha=0.7)
# Indicate the component numbers
for i, m in enumerate(means):
ax.text(m[0], m[1], 'Component %i' % (i + 1),
size=17, horizontalalignment='center',
bbox=dict(alpha=.7, facecolor='w'))
ax.legend(loc='best')
fig.show()

scores = list()
models = list()
for n_components in (3, 4, 5):
# define our hidden Markov model
model = hmm.GaussianHMM(n_components=n_components,
covariance_type='full', n_iter=10)
model.fit(X[:X.shape[0] // 2]) # 50/50 train/validate
models.append(model)
scores.append(model.score(X[X.shape[0] // 2:]))
print(f'Converged: {model.monitor_.converged}'
f'\tScore: {scores[-1]}')
# get the best model
model = models[np.argmax(scores)]
n_states = model.n_components
print(f'The best model had a score of {max(scores)} and {n_states} '
'states')
# use the Viterbi algorithm to predict the most likely sequence of states
# given the model
states = model.predict(X)
Converged: True Score: -1065.5259488089373
Converged: True Score: -904.2908933008515
Converged: True Score: -905.5449538166446
The best model had a score of -904.2908933008515 and 4 states
#讓我們將我們的狀態與生成的狀態和我們的轉換矩陣進行比較,來看我們的模型
# plot model states over time
fig, ax = plt.subplots()
ax.plot(Z, states)
ax.set_title('States compared to generated')
ax.set_xlabel('Generated State')
ax.set_ylabel('Recovered State')
fig.show()
# plot the transition matrix
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 5))
ax1.imshow(gen_model.transmat_, aspect='auto', cmap='spring')
ax1.set_title('Generated Transition Matrix')
ax2.imshow(model.transmat_, aspect='auto', cmap='spring')
ax2.set_title('Recovered Transition Matrix')
for ax in (ax1, ax2):
ax.set_xlabel('State To')
ax.set_ylabel('State From')
fig.tight_layout()
fig.show()


visualizetion_report
該章節主要是講解機器學習的相關視覺化部分,使用Scikit-Plot來實現,主要包括以下幾個部分:
- estimators:用於繪製各種演演算法
- metrics:用於繪製機器學習的onfusion matrix, ROC AUC curves, precision-recall curves等曲線
- cluster:主要用於繪製聚類
- decomposition:主要用於繪製PCA降維
先載入需要的模組:
# 載入需要用到的模組
import scikitplot as skplt
import sklearn
from sklearn.datasets import load_digits, load_boston, load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor, GradientBoostingClassifier, ExtraTreesClassifier
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import sys
print("Scikit Plot Version : ", skplt.__version__)
print("Scikit Learn Version : ", sklearn.__version__)
print("Python Version : ", sys.version)
如果沒有安裝skplt庫的話可以直接:
pip install scikit-plot
載入資料集
手寫資料集
digits = load_digits()
X_digits, Y_digits = digits.data, digits.target
print("Digits Dataset Size : ", X_digits.shape, Y_digits.shape)
X_digits_train, X_digits_test, Y_digits_train, Y_digits_test = train_test_split(X_digits, Y_digits,
train_size=0.8,
stratify=Y_digits,
random_state=1)
print("Digits Train/Test Sizes : ",X_digits_train.shape, X_digits_test.shape, Y_digits_train.shape, Y_digits_test.shape)
Digits Dataset Size : (1797, 64) (1797,)
Digits Train/Test Sizes : (1437, 64) (360, 64) (1437,) (360,)
腫瘤資料集
cancer = load_breast_cancer()
X_cancer, Y_cancer = cancer.data, cancer.target
print("Feautre Names : ", cancer.feature_names)
print("Cancer Dataset Size : ", X_cancer.shape, Y_cancer.shape)
X_cancer_train, X_cancer_test, Y_cancer_train, Y_cancer_test = train_test_split(X_cancer, Y_cancer,
train_size=0.8,
stratify=Y_cancer,
random_state=1)
print("Cancer Train/Test Sizes : ",X_cancer_train.shape, X_cancer_test.shape, Y_cancer_train.shape, Y_cancer_test.shape)
Feautre Names : ['mean radius' 'mean texture' 'mean perimeter' 'mean area'
'mean smoothness' 'mean compactness' 'mean concavity'
'mean concave points' 'mean symmetry' 'mean fractal dimension'
'radius error' 'texture error' 'perimeter error' 'area error'
'smoothness error' 'compactness error' 'concavity error'
'concave points error' 'symmetry error' 'fractal dimension error'
'worst radius' 'worst texture' 'worst perimeter' 'worst area'
'worst smoothness' 'worst compactness' 'worst concavity'
'worst concave points' 'worst symmetry' 'worst fractal dimension']
Cancer Dataset Size : (569, 30) (569,)
Cancer Train/Test Sizes : (455, 30) (114, 30) (455,) (114,)
波士頓房價資料集
boston = load_boston()
X_boston, Y_boston = boston.data, boston.target
print("Boston Dataset Size : ", X_boston.shape, Y_boston.shape)
print("Boston Dataset Features : ", boston.feature_names)
X_boston_train, X_boston_test, Y_boston_train, Y_boston_test = train_test_split(X_boston, Y_boston,
train_size=0.8,
random_state=1)
print("Boston Train/Test Sizes : ",X_boston_train.shape, X_boston_test.shape, Y_boston_train.shape, Y_boston_test.shape)
Boston Dataset Size : (506, 13) (506,)
Boston Dataset Features : ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
Boston Train/Test Sizes : (404, 13) (102, 13) (404,) (102,)
效能視覺化
交叉驗證繪製
我們繪製出邏輯迴歸的交叉驗證學習曲線:
skplt.estimators.plot_learning_curve(LogisticRegression(), X_digits, Y_digits,
cv=7, shuffle=True, scoring="accuracy",
n_jobs=-1, figsize=(6,4), title_fontsize="large", text_fontsize="large",
title="Digits Classification Learning Curve")
plt.show()
skplt.estimators.plot_learning_curve(LinearRegression(), X_boston, Y_boston,
cv=7, shuffle=True, scoring="r2", n_jobs=-1,
figsize=(6,4), title_fontsize="large", text_fontsize="large",
title="Boston Regression Learning Curve ");
plt.show()


需要注意的是因為第二個資料集上的評估指標採用了r2,因此其分數跟第一個有些許不同。
重要性特徵繪製
好的特徵具有的特點為:
- 有區分性,不會跟其他特徵產生冗餘
- 特徵之間相互獨立
- 簡單易於理解
因此重要性特徵繪製就是讓我們能夠直觀看到哪些特徵被函數認為是更加優秀、重要的特徵。
rf_reg = RandomForestRegressor() # 隨機森林
rf_reg.fit(X_boston_train, Y_boston_train)
print(rf_reg.score(X_boston_test, Y_boston_test))
gb_classif = GradientBoostingClassifier() # 梯度提升
gb_classif.fit(X_cancer_train, Y_cancer_train)
print(gb_classif.score(X_cancer_test, Y_cancer_test))
fig = plt.figure(figsize=(15,6))
ax1 = fig.add_subplot(121) # 兩張圖,現在ax1是可以在第一張圖上畫
skplt.estimators.plot_feature_importances(rf_reg, feature_names=boston.feature_names,
title = "Random Forest Regressor Feature Importance",
x_tick_rotation = 90, order="ascending", ax=ax1)
# x_tick_rotation是將x軸的文字旋轉90°
ax2 = fig.add_subplot(122)
skplt.estimators.plot_feature_importances(gb_classif, feature_names=cancer.feature_names,
title="Gradient Boosting Classifier Feature Importance",
x_tick_rotation=90,
ax=ax2);
plt.tight_layout() # 會自動調整子圖引數,使之填充整個影象區域
plt.show()

機器學習度量
混淆矩陣
對於二分類來說,混淆矩陣簡單理解就是下圖:
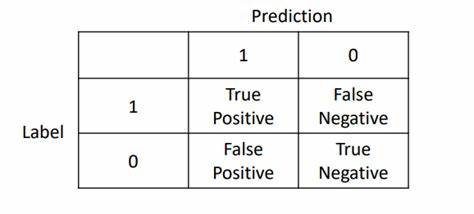
那我們就經常用於計算精準率與召回率,同時計算F1分數。而對於多分類來說相當於是將方陣的維度擴大而已。
log_reg = LogisticRegression()
log_reg.fit(X_digits_train, Y_digits_train)
log_reg.score(X_digits_test, Y_digits_test)
Y_test_pred = log_reg.predict(X_digits_test)
fig = plt.figure(figsize=(15,6))
ax1 = fig.add_subplot(1,2,1)
skplt.metrics.plot_confusion_matrix(Y_digits_test, Y_test_pred, title="Confusion Matrix", cmap="Oranges", ax=ax1)
ax2 = fig.add_subplot(1,2,2)
skplt.metrics.plot_confusion_matrix(Y_digits_test, Y_test_pred,
normalize=True, # 相當於約束到分數
title="Confusion Matrix",
cmap="Purples",
ax=ax2);
plt.show()

第二張圖加了normalize=True,就相當於壓縮到1之間的比例。
ROC、AUC曲線
要了解ROC曲線,我們要從混淆矩陣入手:

其中:
- TP:預測為1,真實為1,真陽率
- FP:預測為1,真實為0,假陽率
- TN:預測為0,真實為0,真陰率
- FN:預測為0,真實為1,假陰率
那麼樣本中真正的正例總數為TP+FN,那麼預測正確的正類佔所有正類的比例為:
同理,真正的反例為FP+TN,那麼預測錯誤的反例佔所有反例的比例為:
另外一個概念是截斷點t,其代表著當模型對於樣本的預測概率大於t時,那麼就歸類為正類,否則歸類為負類。
那麼ROC曲線就是對於資料集,當截斷點t取不同的數值時,TPR和FPR的結果畫出來的二維曲線。
而AUC曲線就是ROC曲線的面積。
Y_test_probs = log_reg.predict_proba(X_digits_test)
skplt.metrics.plot_roc_curve(Y_digits_test, Y_test_probs, title="Digits ROC Curve", figsize=(12,6))
plt.show()
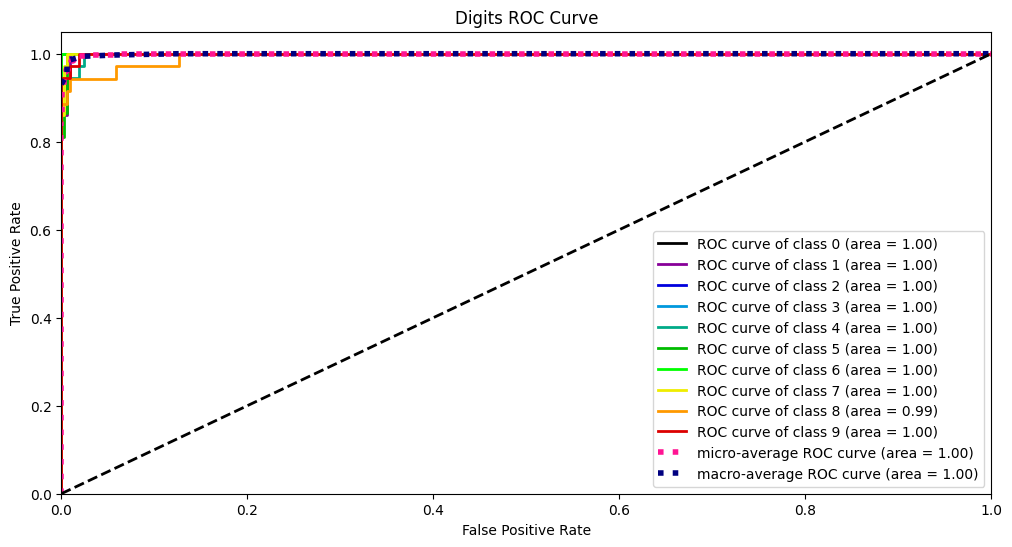
PR曲線
PR曲線的繪製方法跟ROC曲線同理,其選取的兩個指標為精準率和召回率:
然後同樣是選擇不同的截斷點畫出數值。
skplt.metrics.plot_precision_recall_curve(Y_digits_test, Y_test_probs, title="Digits Precision-Recall Curve", figsize=(12,6))
plt.show()

輪廓分析
簡單理解輪廓分析就是用來評判聚類效果的好壞。
kmeans = KMeans(n_clusters=10, random_state=1)
kmeans.fit(X_digits_train, Y_digits_train)
cluster_labels = kmeans.predict(X_digits_test)
skplt.metrics.plot_silhouette(X_digits_test, cluster_labels,figsize=(8,6))
plt.show()

可靠性曲線
檢驗概率模型的可靠性。
lr_probas = LogisticRegression().fit(X_cancer_train, Y_cancer_train).predict_proba(X_cancer_test)
rf_probas = RandomForestClassifier().fit(X_cancer_train, Y_cancer_train).predict_proba(X_cancer_test)
gb_probas = GradientBoostingClassifier().fit(X_cancer_train, Y_cancer_train).predict_proba(X_cancer_test)
et_scores = ExtraTreesClassifier().fit(X_cancer_train, Y_cancer_train).predict_proba(X_cancer_test)
probas_list = [lr_probas, rf_probas, gb_probas, et_scores]
clf_names = ['Logistic Regression', 'Random Forest', 'Gradient Boosting', 'Extra Trees Classifier']
skplt.metrics.plot_calibration_curve(Y_cancer_test,
probas_list,
clf_names, n_bins=15,
figsize=(12,6)
)
plt.show()

KS檢驗
KS檢驗是用來檢驗兩樣本是否服從相同分佈的。
rf = RandomForestClassifier()
rf.fit(X_cancer_train, Y_cancer_train)
Y_cancer_probas = rf.predict_proba(X_cancer_test)
skplt.metrics.plot_ks_statistic(Y_cancer_test, Y_cancer_probas, figsize=(10,6))
plt.show()

累計收益曲線
skplt.metrics.plot_cumulative_gain(Y_cancer_test, Y_cancer_probas, figsize=(10,6))
plt.show()
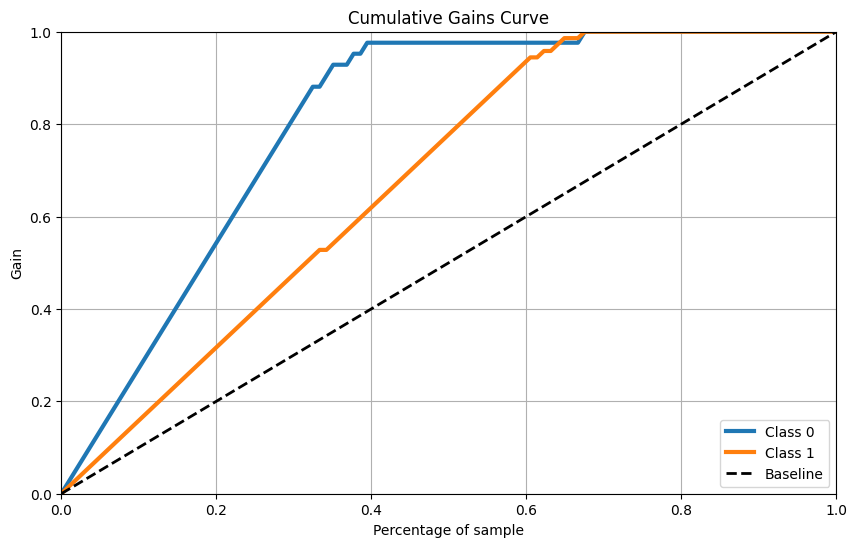
Lift曲線
skplt.metrics.plot_lift_curve(Y_cancer_test, Y_cancer_probas, figsize=(10,6))
plt.show()

聚類方法
手肘法
用來選擇聚類應該選擇的簇數目
skplt.cluster.plot_elbow_curve(KMeans(random_state=1),
X_digits,
cluster_ranges=range(2, 20),
figsize=(8,6))
plt.show()

降維方法
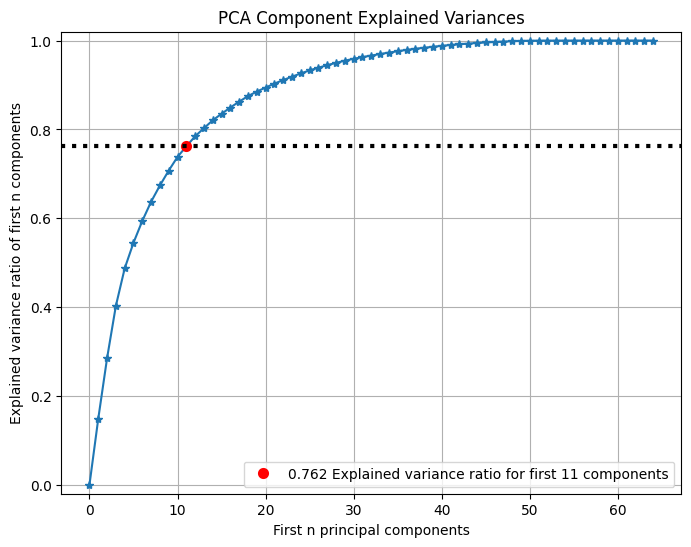
PCA
可以檢視PCA前n個主成分所佔方差比例:
pca = PCA(random_state=1)
pca.fit(X_digits)
skplt.decomposition.plot_pca_component_variance(pca, figsize=(8,6))
plt.show()
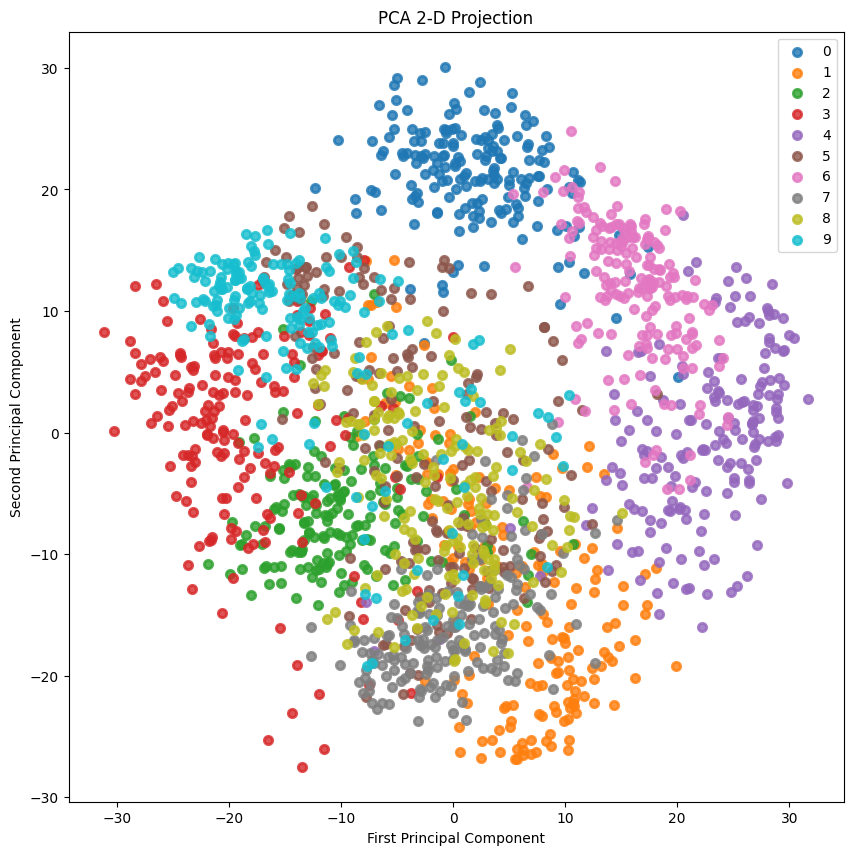
2-D Projection
2D投影:
skplt.decomposition.plot_pca_2d_projection(pca, X_digits, Y_digits,
figsize=(10,10),
cmap="tab10")
plt.show()