說一下 ArrayDeque 和 LinkedList 的區別?

大家好，我是小彭。

在上一篇文章裡，我們聊到了基於連結串列的 Queue 和 Stack 實現 —— LinkedList。那麼 Java 中有沒有基於陣列的 Queue 和 Stack 實現呢？今天我們就來聊聊這個話題。

小彭的 Android 交流群 02 群已經建立啦，掃描文末二維條碼進入~

思維導圖：

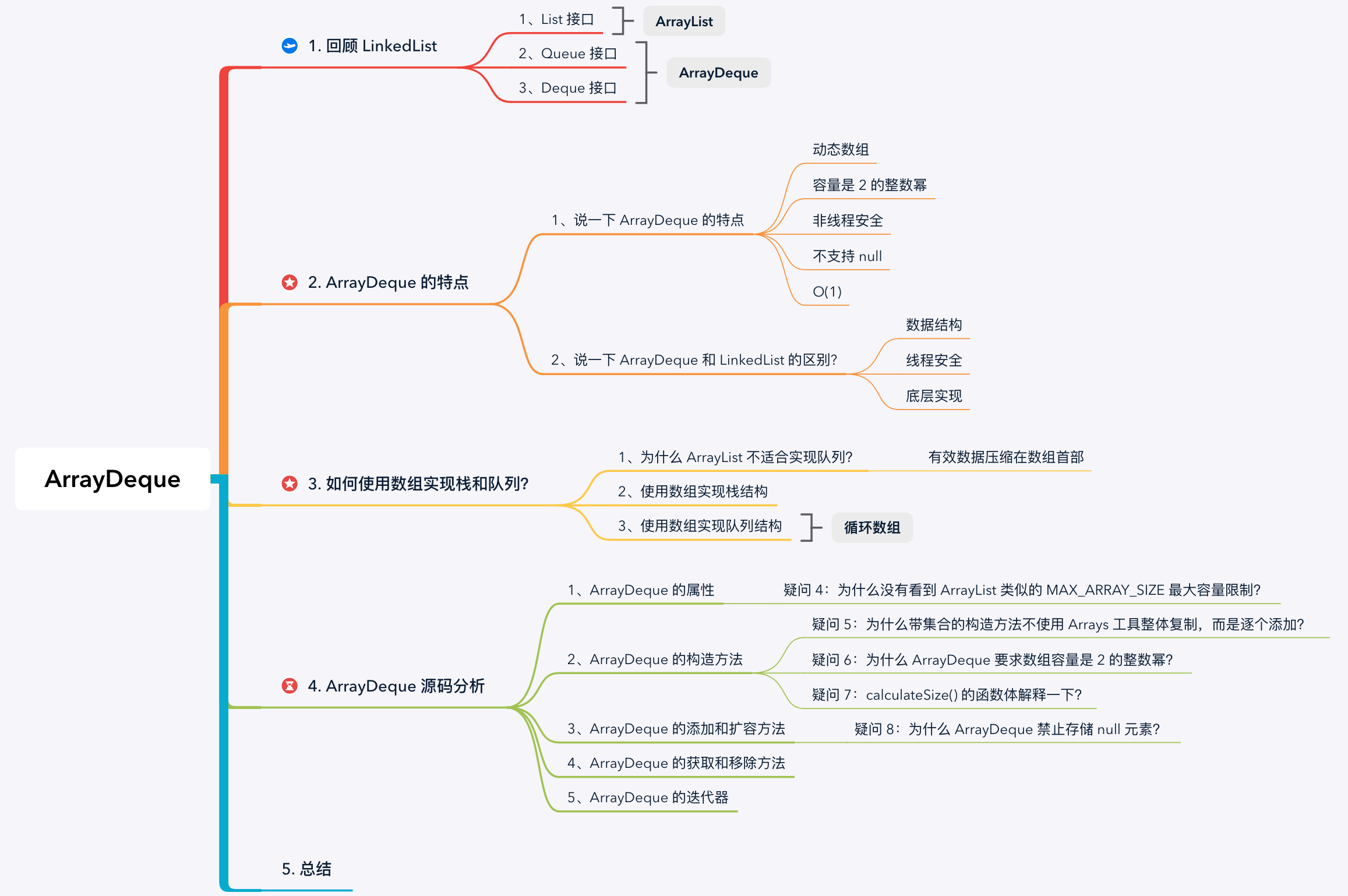
1. 回顧 LinkedList

在資料結構上，LinkedList 不僅實現了與 ArrayList 相同的 List 介面，還實現了 Deque 介面，而我們今天要講的 ArrayDeque 就是實現於 Deque 介面的動態陣列。

Deque 介面表示一個雙端佇列（Double Ended Queue），允許在佇列的首尾兩端操作，所以既能實現佇列行為，也能實現棧行為。

1.1 Queue 介面

Queue 的 API 可以分為 2 類，區別在於方法的拒絕策略上：

拋異常：
- 向空佇列取資料，會丟擲 NoSuchElementException 異常；
- 向容量滿的佇列加資料，會丟擲 IllegalStateException 異常。
返回特殊值：
- 向空佇列取資料，會返回 null；
- 向容量滿的佇列加資料，會返回 false。

拒絕策略	拋異常	返回特殊值
入隊（隊尾）	add(e)	offer(e)
出隊（隊頭）	remove()	poll()
觀察（隊頭）	element()	peek()

1.2 Deque 介面（繼承於 Queue 介面）

Java 沒有提供標準的棧介面（很好奇為什麼不提供），而是放在 Deque 介面中：

拒絕策略	拋異常	等價於
入棧	push(e)	addFirst(e)
出棧	pop()	removeFirst()
觀察（棧頂）	peek()	peekFirst()

除了標準的佇列和棧行為，Deque 介面還提供了 12 個在兩端操作的方法：

拒絕策略	拋異常	返回值
增加	addFirst(e)/ addLast(e)	offerFirst(e)/ offerLast(e)
刪除	removeFirst()/ removeLast()	pollFirst()/ pollLast()
觀察	getFirst()/ getLast()	peekFirst()/ peekLast()

2. ArrayDeque 的特點

2.1 說一下 ArrayDeque 的特點

1、ArrayDeque 是基於動態陣列實現的 Deque 雙端佇列，內部封裝了擴容和資料搬運的邏輯；
2、ArrayDeque 的陣列容量保證是 2 的整數冪；
3、ArrayDeque 不是執行緒安全的；
4、ArrayDeque 不支援 null 元素；
5、ArrayDeque 雖然入棧和入隊有可能會觸發擴容，但從均攤分析上看依然是 O(1) 時間複雜度；

2.2 說一下 ArrayDeque 和 LinkedList 的區別?

1、資料結構： 在資料結構上，ArrayDeque 和 LinkedList 都實現了 Java Deque 雙端佇列介面。但 ArrayDeque 沒有實現了 Java List 列表介面，所以不具備根據索引位置操作的行為；
2、執行緒安全： ArrayDeque 和 LinkedList 都不考慮執行緒同步，不保證執行緒安全；
3、底層實現： 在底層實現上，ArrayDeque 是基於動態陣列的，而 LinkedList 是基於雙向連結串列的。
- 在遍歷速度上： ArrayDeque 是一塊連續記憶體空間，基於區域性性原理能夠更好地命中 CPU 快取行，而 LinkedList 是離散的記憶體空間對快取行不友好；
- 在操作速度上： ArrayDeque 和 LinkedList 的棧和佇列行為都是 O(1) 時間複雜度，ArrayDeque 的入棧和入隊有可能會觸發擴容，但從均攤分析上看依然是 O(1) 時間複雜度；
- 額外記憶體消耗上： ArrayDeque 在陣列的頭指標和尾指標外部有閒置空間，而 LinkedList 在節點上增加了前驅和後繼指標。

3. 如何使用陣列實現棧和佇列？

我們知道棧和佇列都是「操作受限」的線性表：棧是 LIFO，限制在表的一端入棧和出棧。而佇列是 FIFO，限制在表的一端入隊，在另一端出隊。棧和佇列既可以用陣列實現，也可以用連結串列實現：

陣列：用陣列實現時叫作順序棧和順序佇列；
連結串列：用連結串列實現時叫作鏈式棧和鏈式佇列。

3.1 為什麼 ArrayList 不適合實現佇列？

在上一篇文章裡，我們提到了 LinkedList 的多面人生，它即作為 List 的鏈式表，又作為 Queue 的鏈式佇列，又作為「Stack」的鏈式棧，功能很全面。相較之下，ArrayList 卻只作為實現了 List 的順序表，為什麼呢？

這是因為在陣列上同時實現 List 和 Queue 時，無法平衡這兩個行為的效能矛盾。具體來說：ArrayList 不允許底層資料有空洞，所有的有效資料都會 「壓縮」 到底層陣列的首部。所以，使用 ArrayList 開發棧的結構或許合適，可以在陣列的尾部運算元據。但使用 ArrayList 開發佇列就不合適，因為在陣列的首部入隊或出隊需要搬運資料。

3.2 使用陣列實現棧結構

使用陣列實現棧相對容易，因為棧結構的操作被限制在陣列的一端，所以我們可以選擇陣列的尾部作為棧頂，並且使用一個 top 指標記錄棧頂位置：

棧空： top == 0；
棧滿： top == n；
入棧： 將資料新增到棧頂位置，均攤時間複雜度是 O(1)；
出棧： 將棧頂位置移除，時間複雜度是 O(1)；

對於出棧而言，時間複雜度總是 O(1)，但是對於入棧而言，卻不一定。因為當陣列的空間不足（top == n）時，就需要擴容和搬運資料來容納新的資料。此時，時間複雜度就從 O(1) 退化到 O(n)。

對於這種大部分操作時間複雜度很低，只有個別情況下時間複雜度會退化，而且這些操作之間存在很強烈的順序關係的情況，就很適合用 「均攤時間複雜度分析」 了：

假設我們的擴容策略是將陣列擴大到舊陣列的 2 倍，用均攤分析法：

1、對於一個大小為 K 的空陣列，在前 K - 1 次入棧操作中，時間複雜度都是 O(1)；
2、在第 K 次入棧中，由於陣列容量不足，所以我們將陣列擴大為 2K，並且搬運 K 個資料，時間複雜度退化為 O(K)；
3、對於一個大小為 2K 的陣列，在接下來的 K - 1 次入棧操作中，時間複雜度都是 O(1)；
4、在第 2K 次入棧中，由於陣列容量不足，所以我們將陣列擴大為 4K，並且搬運 2K 個資料，時間複雜度再次退化為 O(K)；
5、依此類推。

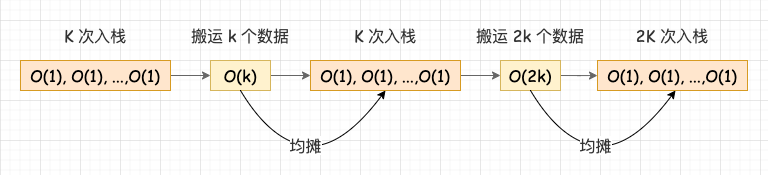
可以看到，在每次搬運 K 個次數後，隨後的 K - 1 次入棧操作就只是簡單的 O(1) 操作，K 次入棧操作涉及到 K 個資料搬運和 K 次賦值操作。那我們從整體看，如果把複雜度較高的 1 次入棧操作的耗時，均攤到其他複雜度較低的操作上，就等於說 1 次入棧操作只需要搬運 1 個資料和 1 次賦值操作，所以入棧的均攤時間複雜度就是 O(1)。

入棧的均攤時間複雜度分析

3.3 使用陣列實現佇列結構

使用陣列實現佇列相對複雜，我們需要一個隊頭指標和一個隊尾指標：

隊空： head == tail；
隊滿： tail == n（並不是真的滿，只是無法填充新資料）；
入隊： 將資料新增到隊尾位置，均攤時間複雜度是 O(1)；
出隊： 將隊頭位置移除，時間複雜度是 O(1)。

對於出隊而言，時間複雜度總是 O(1)。對於入隊而言，當 tail == n 時，就需要擴容和搬運資料來容納新的資料，我們用均攤分析法得出均攤時間複雜度依然是 O(1)，就不重複了。

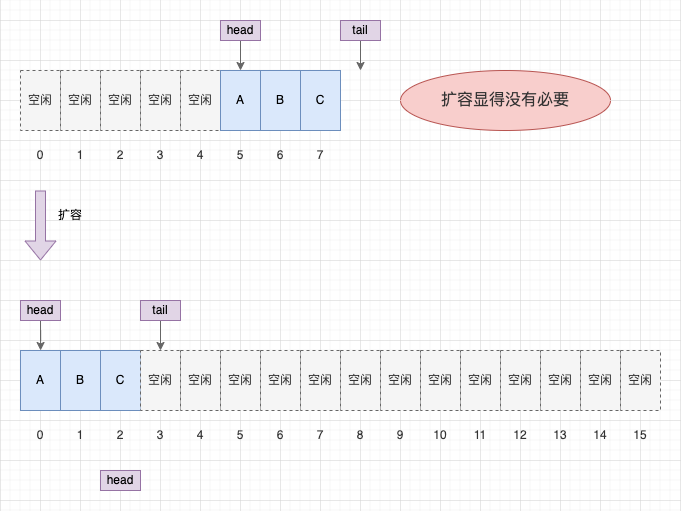
但是我們發現，棧的 top == n 表示棧空間不足，擴容沒有問題，而佇列的 tail == n 卻不一定表示佇列空間不足。因為入隊和出隊發生在不同方向，有可能出現 tail == n 但隊頭依然有非常多剩餘空間的情況。此時，擴容顯得沒有必要。

擴容顯得沒有必要

那麼，怎麼避免沒有必要的擴容和資料搬移呢？—— 迴圈陣列。

我們在邏輯上將陣列的首尾相連，當 tail == n 時，如果陣列頭部還有空閒位置，我們就把 tail 指標調整到陣列頭部，在陣列頭部新增資料。我們下面要分析的 ArrayDeque 資料結構，就是採用了迴圈陣列的實現。

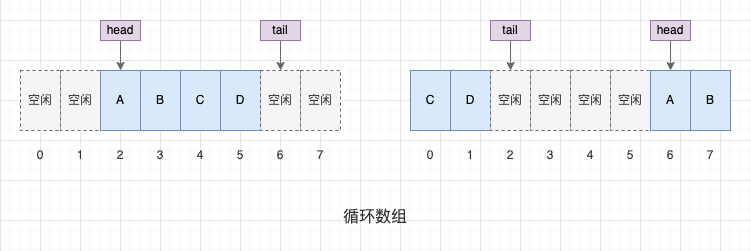
使用迴圈陣列後，佇列空和佇列滿的判斷條件會發生變化：

佇列空： head == tail；
佇列滿： (tail + 1)%size == head，如果 size 是 2 的整數冪，還可以用位運算判斷：(tail + 1) & (size - 1) == head。

理解了使用陣列實現棧和佇列的思路後，下面再來分析 ArrayDeque 的實現原理，就顯得遊刃有餘了。

4. ArrayDeque 原始碼分析

這一節，我們來分析 ArrayDeque 中主要流程的原始碼。

4.1 ArrayDeque 的屬性

ArrayDeque 底層是一個 Object 陣列；
ArrayDeque 用 head 和 tail 指標指向陣列的「隊頭位置」和「隊尾位置」，需要注意 tail 隊尾指標實際上是指向隊尾最後一個有效元素的下一位。

ArrayDeque 的屬性很好理解的，不出意外的話又有小朋友出來舉手提問了：