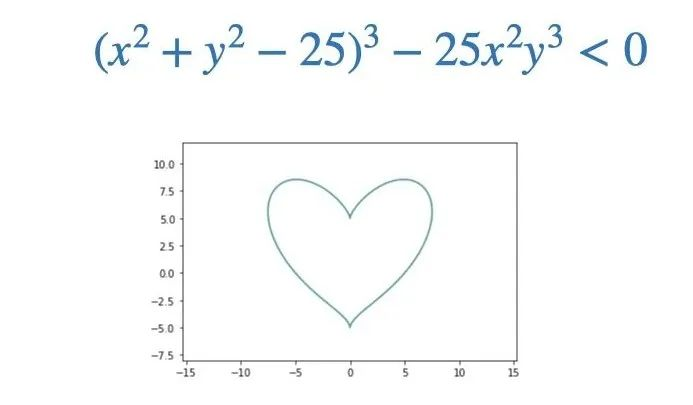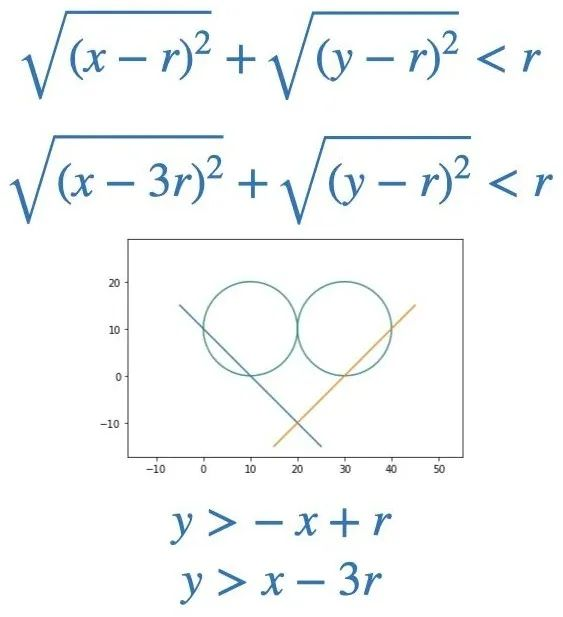電視劇裡的程式碼真能執行嗎?
大家好,歡迎來到 Crossin的程式設計教室 !
前幾天,後臺老有小夥伴留言「愛心程式碼」。這不是Crossin很早之前發過的內容嘛,怎麼最近突然又被人翻出來了?後來才知道,原來是一部有關程式設計師的青春偶像劇《點燃我,溫暖你》在熱播,而劇中有一段關於期中考試要用程式畫一個愛心的橋段。
於是出於好奇,Crossin就去看了這一集(第5集,不用謝)。這一看不要緊,差點把剛吃的雞腿給噴出來--槽點實在太多了!
忍不住做了個歡樂吐槽向的程式碼解讀視訊,在某平臺上被頂到了20個w的瀏覽,也算蹭了一波人家電視劇的熱度吧…
https://www.bilibili.com/video/BV1GY411o72m/
下面是圖文版,給大家分析下劇中出現的「愛心」程式碼,並且來複刻一下最後男主完成的酷炫跳動愛心。
劇中程式碼賞析
- 首先是路人同學的程式碼:
雖然劇中說是「C語言期中考試」,但這位同學的程式碼名叫 draw2.py,一個典型的 Python 檔案,再結合截圖中的 pen.forward、pen.setpos 等方法來看,應該是用 turtle 海龜作相簿來畫愛心。那效果通常是這樣的:
import turtle as t
t.color('red')
t.setheading(50)
t.begin_fill()
t.circle(-100, 170)
t.circle(-300, 40)
t.right(38)
t.circle(-300, 40)
t.circle(-100, 170)
t.end_fill()
t.done()
而不是劇中那個命令列下用1組成的不規則的圖形。
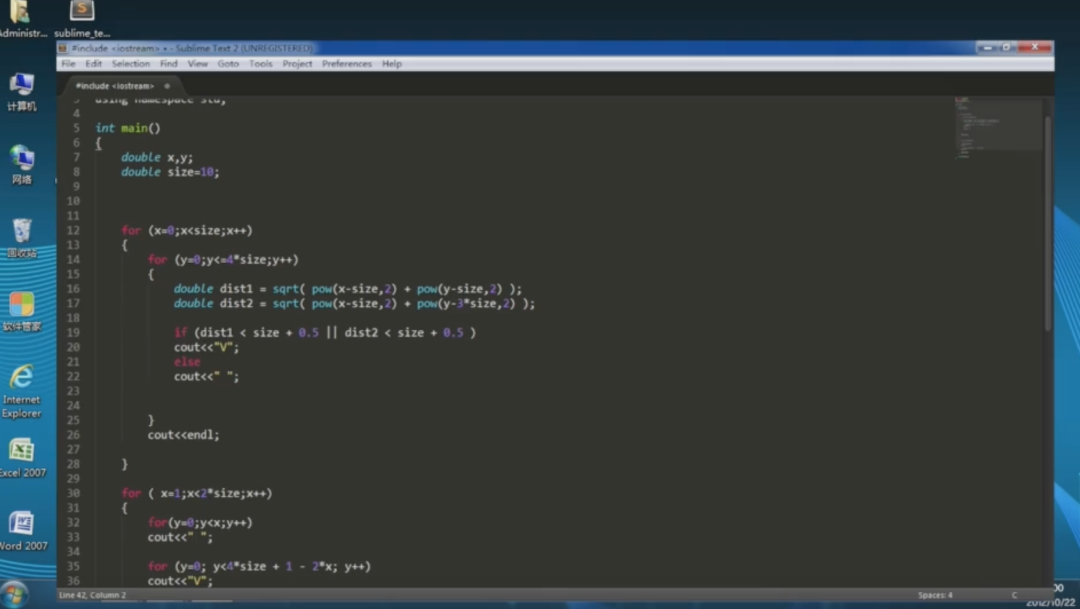
- 然後是課代表向路人同學展示的優秀程式碼:
及所謂的效果:
這確實是C語言程式碼了,但檔案依然是以 .py 為字尾,並且 include 前面沒有加上 #,這顯然是沒法執行的。
裡面的內容是可以畫出愛心的,用是這個愛心曲線公式:
然後遍歷一個1517的方陣,計算每個座標是在曲線內還是曲線外,在內部就輸出#或,外部就是-
用python改寫一下是這樣的:
for y in range(9, -6, -1):
for x in range(-8, 9):
print('*##*'[(x+10)%4] if (x*x+y*y-25)**3 < 25*x*x*y*y*y else '-', end=' ')
print()
效果:
稍微改一下輸出,還能做出前面那個全是1的效果:
for y in range(9, -6, -1):
for x in range(-8, 9):
print('1' if (x*x+y*y-25)**3 < 25*x*x*y*y*y else ' ', end=' ')
print()
但跟劇中所謂的效果相去甚遠。
- 最後是主角狂拽酷炫D炸天的跳動愛心:
程式碼有兩個片段:
但這兩個片段也不C語言,而是C++,且兩段並不是同一個程式,用的方法也完全不一樣。
第一段程式碼跟前面一種思路差不多,只不過沒有直接用一條曲線,而是上半部用兩個圓形,下半部用兩條直線,圍出一個愛心。
改寫成 Python 程式碼:
size = 10
for x in range(size):
for y in range(4*size+1):
dist1 = ((x-size)**2 + (y-size)**2) ** 0.5
dist2 = ((x-size)**2 + (y-3*size)**2) ** 0.5
if dist1 < size + 0.5 or dist2 < size + 0.5:
print('V', end=' ')
else:
print(' ', end=' ')
print()
for x in range(1, 2*size):
for y in range(x):
print(' ', end=' ')
for y in range(4*size+1-2*x):
print('V', end=' ')
print()
執行效果:
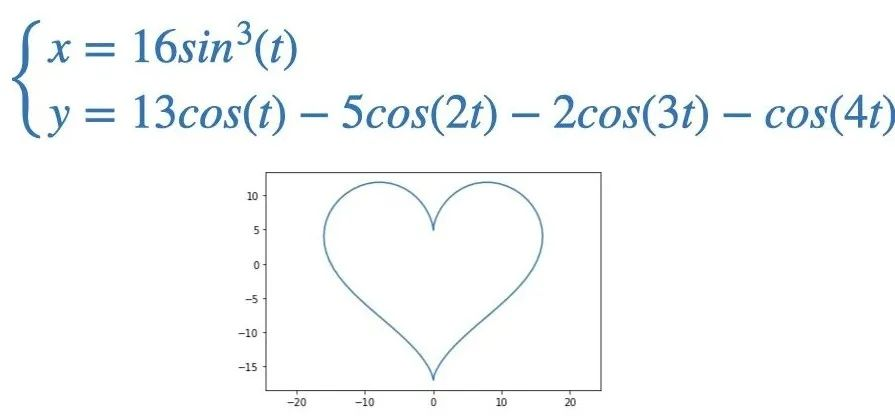
第二段程式碼用的是基於極座標的愛心曲線,是遍歷角度來計算點的位置。公式是:
計算出不同角度對應的點座標,然後把它們連起來,就是一個愛心。
from math import pi, sin, cos
import matplotlib.pyplot as plt
no_pieces = 100
dt = 2*pi/no_pieces
t = 0
vx = []
vy = []
while t <= 2*pi:
vx.append(16*sin(t)**3)
vy.append(13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t))
t += dt
plt.plot(vx, vy)
plt.show()
效果:
程式碼中迴圈時用到的2π是為了保證曲線長度足夠繞一個圈,但其實長一點也無所謂,即使 π=100 也不影響顯示效果,只是相當於同一條曲線畫了很多遍。所以劇中程式碼裡寫下35位小數的π,還被女主用紙筆一字不落地抄寫下來,實在是讓程式設計師無法理解的迷惑行為。
但不管寫再多位的π,上述兩段程式碼都和最終那個跳動的效果差了五百隻羊了個羊。
跳動愛心實現
作為一個總是在寫一些沒什麼亂用的程式碼的程式設計博主,Crossin當然也不會放過這個機會,下面就來挑戰一下用 Python 實現最終的那個效果。
- 想要繪製動態的效果,必定要藉助一些庫的幫助,不然程式碼量肯定會讓你感動得想哭。這裡我們將使用之前 羊了個羊遊戲 裡用過的 pgzero 庫。然後結合最後那個極座標愛心曲執行緒式碼,先繪製出曲線上離散的點。
import pgzrun
from math import pi, sin, cos
no_p = 100
dt = 2*3/no_p
t = 0
x = []
y = []
while t <= 2*3:
x.append(16*sin(t)**3)
y.append(13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t))
t += dt
def draw():
screen.clear()
for i in range(len(x)):
screen.draw.filled_rect(Rect((x[i]*10+400, -y[i]*10+300), (4, 4)), 'pink')
pgzrun.go()
- 把點的數量增加,同時沿著原點到每個點的徑向加一個亂數,並且這個亂數是按照正態分佈來的(半個正態分佈),大概率分佈在曲線上,向曲線內部遞減。這樣,就得到這樣一個隨機分佈的愛心效果。
...
no_p = 20000
...
while t <= 2*pi:
l = 10 - abs(random.gauss(10, 2) - 10)
x.append(l*16*sin(t)**3)
y.append(l*(13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t)))
t += dt
...
- 下面就是讓點動起來,這步是關鍵,也有一點點複雜。為了方便對於每個點進行控制,這裡將每個點自定義成了一個Particle類的範例。
從原理上來說,就是給每個點加一個縮放係數,這個係數是根據時間變化的正弦函數,看起來就會像呼吸的節律一樣。
class Particle():
def __init__(self, pos, size, f):
self.pos = pos
self.pos0 = pos
self.size = size
self.f = f
def draw(self):
screen.draw.filled_rect(Rect((10*self.f*self.pos[0] + 400, -10*self.f*self.pos[1] + 300), self.size), 'hot pink')
def update(self, t):
df = 1 + (2 - 1.5) * sin(t * 3) / 8
self.pos = self.pos0[0] * df, self.pos0[1] * df
...
t = 0
def draw():
screen.clear()
for p in particles:
p.draw()
def update(dt):
global t
t += dt
for p in particles:
p.update(t)
- 劇中愛心跳動時,靠中間的點波動的幅度更大,有一種擴張的效果。所以再根據每個點距離原點的遠近,再加上一個係數,離得越近,係數越大。
class Particle():
...
def update(self, t):
df = 1 + (2 - 1.5 * self.f) * sin(t * 3) / 8
self.pos = self.pos0[0] * df, self.pos0[1] * df
- 最後再用同樣的方法畫一個更大一點的愛心,這個愛心不需要跳動,只要每一幀隨機繪製就可以了。
def draw():
...
t = 0
while t < 2*pi:
f = random.gauss(1.1, 0.1)
x = 16*sin(t)**3
y = 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t)
size = (random.uniform(0.5,2.5), random.uniform(0.5,2.5))
screen.draw.filled_rect(Rect((10*f*x + 400, -10*f*y + 300), size), 'hot pink')
t += dt * 3
合在一起,搞定!
總結一下,就是在原本的基礎愛心曲線上加上一個正態分佈的隨機量、一個隨時間變化的正弦函數和一個跟距離成反比的係數,外面再套一層更大的隨機愛心,就得到類似劇中的跳動愛心效果。
但話說回來,真有人會在考場上這麼幹嗎?
除非真的是超級大學霸,不然就是食堂伙食太好--
吃太飽撐的……
程式碼已開源:python666.cn/c/9
如二創釋出請註明程式碼來源:Crossin的程式設計教室