JDK原始碼分析實戰系列-PriorityQueue
完全二元樹
一棵深度為k的有n個結點的二元樹,對樹中的結點按從上至下、從左到右的順序進行編號,如果編號為i(1≤i≤n)的結點與滿二元樹中編號為i的結點在二元樹中的位置相同,則這棵二元樹稱為完全二元樹。
特殊之處是這個型別可以通過陣列來實現,一個節點的兩個子節點的只需要計算下標獲得,分別是[2*n+1]和[2*(n+1)],想象一下一個陣列緊湊儲存節點的效果,陣列沒有任何空間浪費的話,看起來是那麼完美,因為使用陣列實現就不需要儲存子節點和父節點的地址了。
堆
百度百科了一下:
- 堆中某個結點的值總是不大於或不小於其父結點的值。
- 堆總是一棵完全二元樹。
PriorityQueue
Priority queue represented as a balanced binary heap: the two children of queue[n] are queue[2n+1] and queue[2(n+1)]
The element with the lowest value is in queue[0], assuming the queue is nonempty
優先順序佇列在JDK中有一個教科書式的示範實現,以上是JDK原始碼對實現的註釋。和前面介紹的完全二元樹一樣,儲存元素時使用的父子節點在陣列中的下標使用[2n+1] 和[2(n+1)]的公式計算,如果是反過來算父節點的下標位置公式是:(n-1)>>> 1。
PriorityQueue就是一個小頂堆的實現,也是被認為實現優先順序佇列最高效的方式。
下面就是對PriorityQueue的實現分析。
插入元素操作
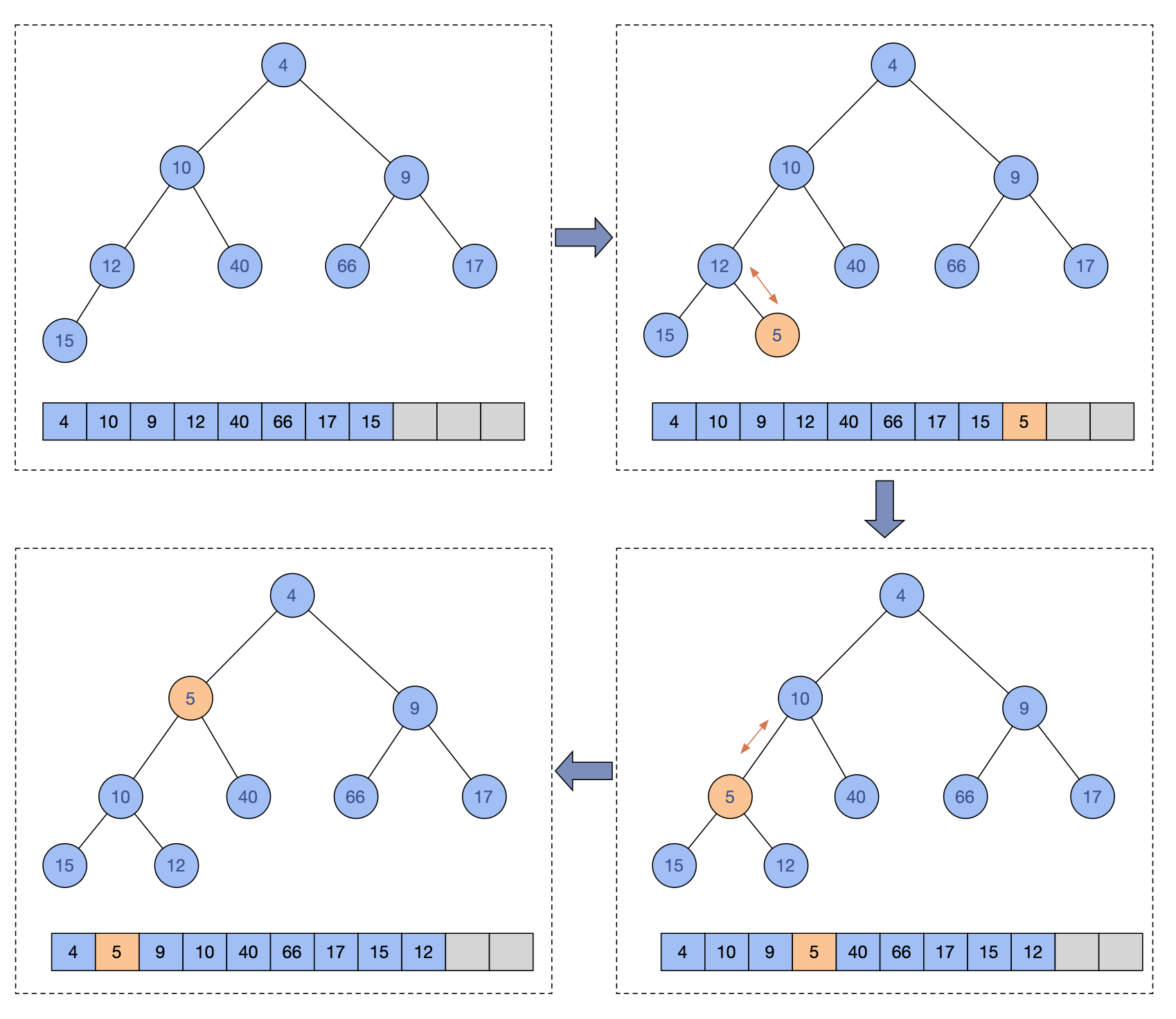
插入元素的時候先判斷了是否需要擴容,擴容在後面會提到,核心的邏輯是,元素先加到隊尾,然後進行siftUp,使得新加入的元素調整成符合小頂堆的要求。
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
// 擴容
grow(i + 1);
// 最後一個位置下標加1
size = i + 1;
if (i == 0)
// 第一個元素情況
queue[0] = e;
else
// 節點從尾部加入,然後上移操作,直到保持堆處於正確狀態
siftUp(i, e);
return true;
}
PriorityQueue支援元素實現Comparable,也支援初始化時傳入一個Comparator作為比較運算元。所以siftUp區分了兩種實現,都是差不多的,選一個分析一下,siftUp是調整堆的核心操作,這個操作是把元素從引數k位置開始,和父節點進行比較,如果比父節點小,就和父節點交換,不斷重複,直到父節點比自己大或等於,或者自己已經移動到根節點才停止。
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
// 父節點下標
int parent = (k - 1) >>> 1;
// 父節點值
Object e = queue[parent];
// 新增值大於父節點,那就符合成為這個父節點下子節點的要求
if (key.compareTo((E) e) >= 0)
break;
// 當前的父節點下移動
queue[k] = e;
// k改為父節點下標,下一輪迴圈從父節點開始
k = parent;
}
// 退出迴圈出來的,直接把值賦值給k下標即可
queue[k] = key;
}
每增加一個元素,PriorityQueue就需要調整一次以確保小頂堆的排序,寫操作是有一定消耗的。
結合siftUp方法實現,再看一個插入一個元素的流程示意圖:
查詢元素
查詢操作其實就是遍歷陣列找出元素,不要感到驚訝,就是這麼樸素無華,本質原因PriorityQueue的特性並不是快速定位某個元素的。是這裡可能會有誤解以為堆這種資料結構保證了左節點必然小於或大於右節點這樣的規則,那麼查詢一個值可以是更有效率的二分法方式,而事實上堆並沒有這個特性,所以查詢一個元素就需要直接遍歷全部元素。
public boolean contains(Object o) {
return indexOf(o) != -1;
}
private int indexOf(Object o) {
if (o != null) {
// 遍歷陣列
for (int i = 0; i < size; i++)
// 比較查出想要找的元素
if (o.equals(queue[i]))
return i;
}
// 如果不存在就返回-1 contains判斷是否不等於-1
return -1;
}
這樣就知道contains操作實踐複雜度是O(n),資料量大的話需要考慮避免使用。
刪除元素操作
刪除操作的流程:先查出元素在陣列中的下標,然後從陣列中刪除這個下標的元素,最後,此時這個堆中間就可能出現缺失一個元素的情況,所以需要進行調整這個堆的元素最終成為一個正確的小頂堆。前面查詢刪除比較簡單,關鍵是調整環節,下面詳細解析一下這部分的原始碼:
public boolean remove(Object o) {
int i = indexOf(o);
if (i == -1)
return false;
else {
removeAt(i);
return true;
}
}
private E removeAt(int i) {
// assert i >= 0 && i < size;
modCount++;
// 陣列最後一個元素的下標
int s = --size;
if (s == i) // removed last element
queue[i] = null;
else {
// 陣列最後一個元素的值
E moved = (E) queue[s];
// 將陣列最後一個元素從位置上刪除
queue[s] = null;
// 將元素從要刪除的陣列下標i位置開始下移
// 下移只能在i下標是非葉子節點情況,並且子節點大於移動的值才會發生下移
siftDown(i, moved);
// 這個判斷表示如果i下標已經是葉子節點而沒有下移,或者i下標不是葉子節點在和子節點比較後而無需下移
if (queue[i] == moved) {
// 既然沒有進行下移,那麼說明在i這個位置上,放moved這個值是最小的,但是還不能保證和自己的父節點比是不是大於等於的,所以需要進行上移的操作
siftUp(i, moved);
// 上移結束後,如果i下標的元素和moved不一致證明在這個i下標之前的元素已經因為上移操作有了變化,而返回這個從陣列最後取得的元素
if (queue[i] != moved)
return moved;
}
}
return null;
}
從一個堆中刪除一個元素後,就會出現一個空缺的位置,接下去怎麼操作呢?原始碼中是將陣列中最後一個元素來填補這個空缺,然後從這個元素開始進行下移(siftDown)操作,如果沒有移動,就進行上移(siftUp),無論上移還是下移都是在通過元素的交換最終確定填補的元素應該處於的的適當位置,所以最終不會出現空缺的情況,並且能夠調整出一個正確的新堆。
和siftUp相似,siftDown操作也是區分兩種方式,這裡也只挑一個看就行了。
private void siftDown(int k, E x) {
if (comparator != null)
siftDownUsingComparator(k, x);
else
siftDownComparable(k, x);
}
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x;
// 這個half是最後一個節點無符號右移計算得到
// 這個計算得到的位置是葉子節點的開始位置,所以下面的while條件是小於這個位置
int half = size >>> 1; // loop while a non-leaf
// 因為這裡是操作下移,如果已經是葉子節點就沒有下移的必要了
while (k < half) {
// 自己左側子節點下標
int child = (k << 1) + 1; // assume left child is least
// 自己左側子節點值
Object c = queue[child];
// 自己右側子節點下標
int right = child + 1;
// 右節點可能沒有,比如左節點已經是陣列最後一個值了,所以判斷了一下right < size
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
// 如果如果左節點值大於右節點值,就把更小的右節點值賦值給c
c = queue[child = right];
if (key.compareTo((E) c) <= 0)
// 如果自己比左節點值小,說明不能下移了,就退出迴圈
break;
// 執行到這裡,說明自己作為父節點,並不比子節點小
// 那麼就把前面從左右子節點中找出來最小的值賦值給k下標的位置
queue[k] = c;
// k值變更為較小的值的下標
k = child;
}
// 迴圈退出後,k下標的位置放自己
queue[k] = key;
}
siftDown它的核心邏輯是將一個元素往樹的下層進行比較,找到比自己小的就進行交換。注意,這種比較是需要比較自己子節點的左右節點的,畢竟這棵樹只保證父節點小於子節點,並不保證左右的節點大小順序。
圖例示意一個刪除操作:
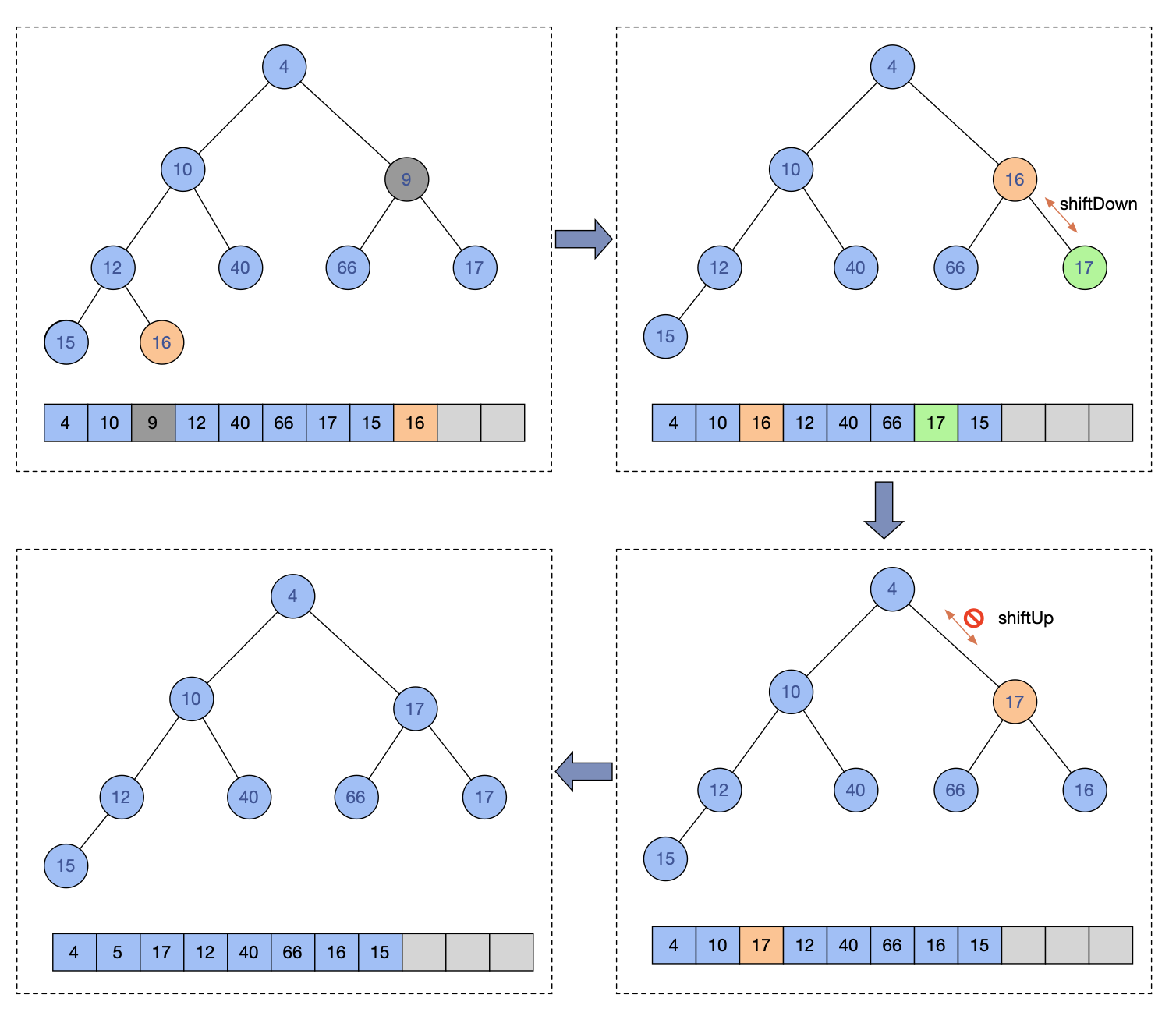
刪除9值節點,把16節點先移動到刪除的下標,然後進行shiftDown,發現是右節點更小,就進行交換,然後刪除下標節點進行shiftUp操作,發現不能在上移,就結束操作。
獲取頂部元素
poll是肯定要用的方法,畢竟花了這麼大勁把最小值排到了根節點上。
可是取出根節點的元素,又會出現少一個元素的情況,按照上面的經驗,肯定是那陣列最後的元素,放到根節點上來,然後進行下移操作就行了,因為已經是從根上開始,所以沒有上移的情況再需要考慮了。
public E poll() {
// 空的情況
if (size == 0)
return null;
// 陣列有值的最後一個下標
int s = --size;
modCount++;
// 根節點,返回值
E result = (E) queue[0];
// 最後一個元素
E x = (E) queue[s];
// 清空根節點
queue[s] = null;
if (s != 0)
// 下移
siftDown(0, x);
return result;
}
擴容
在插入資料的時候就會先判斷是否需要擴容,容量不足是容器都需要面對的問題,畢竟作為專業選手,合理使用資源是時刻需要注意的。
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
// 64區分兩種擴容數量策略
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// overflow-conscious code
// 雖然是無限優先順序佇列,最大的容量溢位還是要控制的
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
// minCapacity 是size+1獲得 如果此時size已經是MAX_VALUE 那麼minCapacity會變成負數,溢位丟擲OutOfMemoryError異常
if (minCapacity < 0) // overflow
throw new OutOfMemoryError();
return (minCapacity > MAX_ARRAY_SIZE) ?
Integer.MAX_VALUE :
MAX_ARRAY_SIZE;
}
如果想用大頂堆怎麼辦?
非常簡單,比較上元素實現Comparable的時候反著來就行了。
關於如何獲得順序資料
我們已經清楚PriorityQueue使用陣列儲存,按照陣列下標順序便利並不是順序的,這一點是顯而易見的。而不斷獲取頭節點並刪除,也可以遍歷一個ProirityQueue,這種遍歷方式就可以保證這個資料結構的順序輸出,因為ProirityQueue在操作的時候始終保證一點,頭節點是最小元素。
雖然這一點過於細節,因為有助於更好的理解,就展開一下,如果通過迭代器遍歷的時候,相當對陣列從頭到尾進行遍歷,所以並不是確保順序性,如果使用poll()遍歷,那麼是確保了順序性,因為每次poll的時候相當於都需要調整出最小值到頭節點上。
第一種遍歷方式:
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(10);
for (int i = 10; i >=2; i--) {
priorityQueue.add(i);
}
for (Integer e : priorityQueue) {
System.out.print(e + ",");
}
}
輸出結果:2,3,5,4,8,9,6,10,7,
第二種遍歷方式:
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(10);
for (int i = 10; i >=2; i--) {
priorityQueue.add(i);
}
Integer t;
while ((t = priorityQueue.poll()) != null) {
System.out.print(t + ",");
}
}
輸出結果:2,3,4,5,6,7,8,9,10,
排序複雜度:
這裡堆PriorityQueue排序的複雜度做一個簡單分析,建堆後,通過poll遍歷一個有序的元素列表,這個過程每次都是把最後的元素放到根節點上進行下移,排序過程的時間複雜度是O(nlogn),建堆的時間複雜度O(n),整體的時間複雜度O(nlogn)。
但是我們在排序過程中每次都是把最後面的元素移動到根節點,理論上來說這個移動的元素必然是需要移動的,這一點是有優化空間的。可以看出,堆的排序交換次數是偏多的。
使用場景
1,高效能定時器 這個在jdk中的ScheduledExecutorService有使用,以後分析可以關聯起來。
2,Top K 問題,實際業務研發會使用到。