決策樹(二):後剪枝,連續值處理,資料載入器:DataLoader和模型評估
2022-11-20 15:03:35
在上一篇文章中,我們實現了樹的構造,在下面的內容中,我們將中心放在以下幾個方面
1.剪枝
2.連續值處理
3.資料載入器:DataLoader
4.模型評估
一,後剪枝
• 為什麼剪枝 –「剪枝」是決策樹學習演演算法對付「過擬合」的主要手段,可通過「剪枝」來一定程度避免因決策分支過多,以致於把訓練集自身的一些特點當做所有資料都具有的一般性質而導致的過擬合
• 剪枝的基本策略
–預剪枝
–後剪枝
我選擇的是後剪枝,也就是先構造出完整的二元樹,最後在回過頭來剪掉其中一部分節點
後剪枝方法:
1.資料量太少的節點剪掉,可以防止減小誤差對模型的影響,降低過擬合風險,提高泛化能力
2.限制樹的的深度
3.小於先驗概率的節點剪掉,如果一個特徵判斷的能力甚至低於先驗概率,那麼就沒有必要存在
• 後剪枝的優缺點
•優點
–後剪枝比預剪枝保留了更多的分支,欠擬合風險小
,泛化效能往往優於預剪枝決策樹
•缺點
–訓練時間開銷大:後剪枝過程是在生成完全決策樹
之後進行的,需要自底向上對所有非葉結點逐一計算
程式碼實現
# 後剪枝 def post_pruning(self,tree_dict,data,key=None): def processing_data(data,col_name,value): inx=data[col_name]==value return data[inx] for k in tree_dict: # 如果不是葉子節點 if not isinstance(tree_dict[k], str): if key in self.data.columns: # 遞迴遍歷所有節點 flag, count = self.post_pruning(tree_dict[k],data=processing_data(data,key,k),key=k) else:flag, count = self.post_pruning(tree_dict[k], data=data, key=k) # 如果知道葉子節點可以合併,返回兩次找到爺爺節點,把父節點變為save或not save if count == 1: return flag, count + 1 elif count == 2: tree_dict[k] = flag #葉子節點,判斷資料是否大於閾值 elif data.shape[0]<self.num_threshold: if len(data[data[self.target]==0])>=len(data[self.target])/2: return "not save",1 else:return "save",1 # 葉子節點,判斷是否都相同 elif np.array([v == "save" for v in tree_dict.values()]).all(): return "save", 1 elif np.array([v == "not save" for v in tree_dict.values()]).all(): return "not save", 1 continue return tree_dict, 0
二,連續值處理
處理方法:
• 連續屬性取值數目非有限,無法直接進行劃分;
• 離散化(二分法)
– 第一步:將連續屬性 a 在樣本集 D 上出現 n 個不同的取值從小到大排列,記為 a 1 , a 2 , ..., a n 。基於劃分點t,可將D分為子集Dt +和Dt-,其中Dt-包含那些在屬性a上取值不大於t的樣本,Dt+包含那些在屬性 a上取值大於t的樣本。考慮包含n-1個元素的候選劃分點集合即把區間[a i , a i-1) 的中位點 (a i+a i-1)/2作為候選劃分點
– 第二步:採用離散屬性值方法,計算這些劃分點的增益,選取最優的劃分點進行樣本集合的劃分:其中Gain(D, a, t)是樣本集D基於劃分點 t 二分後的資訊增益,於是, 就可選擇使Gain(D, a, t)最大化的劃分點
程式碼實現
def process_continue_value(x,y,total_entropy): ''' :param x: data:pd :param y: data[Survived]:pd :param total_entropy: int :return: 處理後的data ''' data=x["Age"] total_data=len(data) mean_list=[] gain_list=[] data=np.array(data) data.sort() unique_data=np.unique(data) for i in range(len(unique_data)-1): mean_list.append((unique_data[i]+unique_data[i+1])/2) for v in mean_list: x1_index=np.where(data>=v)[0] x2_index=np.where(data<v)[0] kind_y1=y[x1_index] kind_y2=y[x2_index] len_kind1=len(kind_y1) len_kind2 = len(kind_y2) part_gain=total_entropy-(len_kind1/total_data)*entropy(kind_y1)-(len_kind2/total_data)*entropy(kind_y2) gain_list.append(part_gain) x["Age"]=[0 if i<mean_list[np.argmax(gain_list)] else 1 for i in x["Age"]] return x
三,資料載入器:DataLoader
構造類資料載入器,傳入data自動劃分好train 和test,傳入引數設定train和test比例,亂數種子,實現劃分
程式碼實現
class DataLoader(object): def __init__(self,data:"pd",random_seed=None,test_size=0.33): self.data=data self.test_size=test_size self.random_seed=random_seed if random_seed is not None else None def __getitem__(self, index): return self.data.iloc[index,:] def __len__(self): return len(self.data) def split_data(self): if self.random_seed is not None: np.random.seed(self.random_seed) train_data_idx=np.random.randint(0,len(self.data),size=int(len(self.data)*(1-self.test_size))) test_data_idx=np.random.randint(0,len(self.data),size=int(len(self.data)*self.test_size)) train_data=self.data.iloc[train_data_idx,:] test_data=self.data.iloc[test_data_idx,:] return train_data,test_data
四,模型評估
模型的好壞我們無法肉眼觀察,需要在測試集中測試,按照構建的決策樹做決策,與真實值比較,得出準確率
程式碼實現
def evaluator(self,tree_dict, test_data: "pd", target_name): #調換資料順序,按照資訊增益由大到小 columns=test_data.columns new_columns=[columns[i] for i in self.gain.argsort()[::-1]] new_columns.append(target_name) #改變順序 test_data=test_data.reindex(columns=new_columns) right=0 #遍歷test_data中每一行資料 for index,row in test_data.iterrows(): temp_tree = tree_dict #根據test_data做選擇 for name in new_columns: choice=row[name] #如果沒有當前分支則跳過 if choice not in temp_tree[name].keys(): value=None break value=temp_tree[name][choice] temp_tree=value if value in["save","not save"]: #將y和pred_y同一 value=0 if value=="not save" else 1 break if value==row[target_name]: right+=1 accuracy = right/len(test_data) return accuracy
五,總結
首先,先把程式碼跑的資料截圖展示以下
1.未剪枝準確率:0.3299319727891156
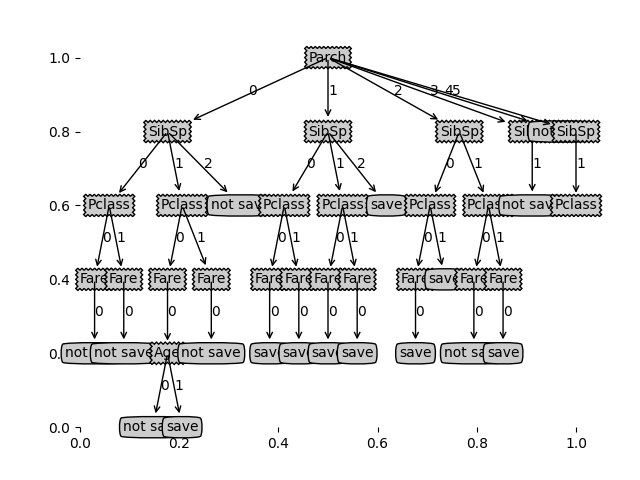
2.剪枝後準確率:0.6190476190476191

對比分析可見,剪枝後準確率大大提升
總結反思:1.在編寫程式碼時,總是會出現各種錯誤,只有細心細心再細心,才能走向成功
2.在此次程式碼中運用大量遞迴,由於剛開始資料結構掌握的不熟練,吃了很多虧
3.在確定類時,剛開始沒有構思好,導致後續整合時,走了彎路。之後最好先畫類圖,再動手是實現程式碼
最後,全部程式碼如下,資料在上一篇文章中已放出
from sklearn.model_selection import train_test_split import numpy as np import pandas as pd from graphviz import Digraph import matplotlib.pyplot as plt import random # 定義文字方塊和箭頭格式 decisionNode = dict(boxstyle="sawtooth", fc="0.8") leafNode = dict(boxstyle="round4", fc="0.8") arrow_args = dict(arrowstyle="<-") ## 繪製帶箭頭的註解############## def plotNode(nodeTxt, centerPt, parentPt, nodeType): createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) ## PLOTTREE################################# ## 在父子節點間填充文字資訊 def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0] yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString) ## 獲取葉節點的數目和樹的層數####################### def getNumLeafs(myTree): numLeafs = 0 firstStr = list(myTree.keys())[0]#找到輸入的第一個元素 secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': numLeafs += getNumLeafs(secondDict[key]) else: numLeafs += 1 return numLeafs def getTreeDepth(myTree): maxDepth = 0 firstStr = list(myTree.keys())[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': thisDepth = 1 + getTreeDepth(secondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth def plotTree(myTree, parentPt, nodeTxt): # 計算寬與高 numLeafs = getNumLeafs(myTree) depth = getTreeDepth(myTree) firstStr = list(myTree.keys())[0] cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff) # 標記子節點屬性 plotMidText(cntrPt, parentPt, nodeTxt) plotNode(firstStr, cntrPt, parentPt, decisionNode) secondDict = myTree[firstStr] # 減少y偏移 plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in secondDict.keys(): if type(secondDict[key]) == dict: plotTree(secondDict[key], cntrPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD def process(data): #資料處理 data.drop("Embarked",inplace=True,axis=1) x=data[["Age","Pclass","Sex","SibSp","Parch","Fare"]] y=data["Survived"] x["Pclass"] = x["Pclass"] - 1 x["SibSp"].fillna(x["SibSp"].mean(),inplace=True)#將預設的用平均值填充 x["Parch"].fillna(x["Parch"].mean(),inplace=True) x["Age"].fillna(x["Age"].mean(),inplace=True) #將大於平均值的設為1 x["Fare"]=[1 if i>np.array(x["Fare"]).mean() else 0 for i in x["Fare"] ] #將sex轉為1和0 x["Sex"]=pd.factorize(x["Sex"])[0].astype(np.uint16) return x,y def process_data(data): data = data[["Age", "Pclass", "Sex", "SibSp", "Parch", "Fare","Survived"]] #使得Pclass從0開始 data["Pclass"]=data["Pclass"]-1 data["Fare"] = [1 if i > np.max(data["Fare"] / 2) else 0 for i in data["Fare"]] data["Sex"] = pd.factorize(data["Sex"])[0].astype(np.uint16) data["SibSp"].fillna(data["SibSp"].mean(),inplace=True)#將預設的用平均值填充 data["Parch"].fillna(data["Parch"].mean(),inplace=True) data["Age"].fillna(data["Age"].mean(), inplace=True) return data #計算資訊熵 def entropy(data): total_len=len(data) len_1=np.where(data==1)[0].shape[0] len_0=len(data)-len_1 # 出現問題:部分資料會返回nan # 探索原因:當概率很小時,取對數後結果趨於負無窮大。 # 解決方法:改變浮點數的精度為1e - 5 p1=len_1/total_len+1e-5 p0=len_0/total_len+1e-5 entro=-np.sum([p0*np.log2(p0),p1*np.log2(p1)]) return entro def process_continue_value(x,y,total_entropy): ''' :param x: data:pd :param y: data[Survived]:pd :param total_entropy: int :return: 處理後的data ''' data=x["Age"] total_data=len(data) mean_list=[] gain_list=[] data=np.array(data) data.sort() unique_data=np.unique(data) for i in range(len(unique_data)-1): mean_list.append((unique_data[i]+unique_data[i+1])/2) for v in mean_list: x1_index=np.where(data>=v)[0] x2_index=np.where(data<v)[0] kind_y1=y[x1_index] kind_y2=y[x2_index] len_kind1=len(kind_y1) len_kind2 = len(kind_y2) part_gain=total_entropy-(len_kind1/total_data)*entropy(kind_y1)-(len_kind2/total_data)*entropy(kind_y2) gain_list.append(part_gain) x["Age"]=[0 if i<mean_list[np.argmax(gain_list)] else 1 for i in x["Age"]] return x #計算資訊增益 def gain(total_entropy,x,y): gain=[] total_data=len(y) # #將特徵轉為數位 # for f in x: # x[f] = pd.factorize(x[f])[0].astype(np.uint16) #計算每一個的gain for feature in x: # print("\n",feature) part_entropy = [] for kind in np.unique(x[feature]): # print("kind:",kind) x_index=np.where(x[feature]==kind)[0] kind_y=y[x_index] len_kind=len(kind_y) # print("len_kind:",len_kind) # print("獲救人數:",len(np.where(kind_y==1)[0])) part_entropy.append((len_kind/total_data)*entropy(kind_y)) gain.append(total_entropy-np.sum(part_entropy)) return gain class TreeNode(object): def __init__(self,name,parent=None): self.name=name self.parent=parent self.children={} #重寫,返回節點名稱 def __repr__(self): return "TreeNode(%s)"%self.name def add_child(self,child,idx): self.children[idx]=child def print_tree(self,root:"TreeNode",leval=0): print("第", leval, "層\n") if root.parent==None: print(root) if root.children: # print(root.name,":",end="") print(root.children.values()) #將每一層的節點全部輸出 #深度優先遍歷 for child in root.children.values(): self.print_tree(child,leval+1) print("\n") #獲得tree的字典 def get_tree_dict(self,root,data=None): def split_data(data,feature,value): inx=data[feature]==value return data[inx] #如果不是TreeNode型別,其實就是「empty」,就停止向下延伸 if not isinstance(root,TreeNode): return #如果沒有資料,標記為empty if data.empty: return "empty" #葉子節點時,那種多就標記為哪一種 if root.children=={}: if len(data[data["Survived"]==0])>=len(data["Survived"])/2: return "not save" else : return "save" # # 類別完全相同,停止劃分 if len(data[data["Survived"]==0])==len(data["Survived"]): #如果data["Survived"]全為0 return "not save" elif len(data[data["Survived"]==1])==len(data["Survived"]): # 如果data["Survived"]全為1 return "save" tree = {root.name: {}} for key in root.children: value=self.get_tree_dict(root.children[key],data=split_data(data,root.name,key)) #如果下個節點為empty,就不生成新的節點 if value=="empty": continue #遞迴,類似於dfs tree[root.name][key]=value return tree class DecisionTree(object): def __init__(self,gain,data:"pd.DataFrame",target,max_depth=None,num_threshold=5): self.prior_probability=len(np.where(target==1)[0])/len(target) self.max_depth=max_depth self.num_threshold=num_threshold self.depth=0 self.data=data # self.gain=np.array(gain.sort(reverse=True)) self.gain=np.array(gain) self.x=data.drop(target,axis=1) self.target=target # 深度優先建樹 def init(self): def dfs(node, map, leval=1): # leval=0為根節點 if leval < len(map): # 獲取當前 cur_name = map[leval] node_children = np.unique(self.x[cur_name]) cur_node = TreeNode(cur_name, node) for i in node_children: dfs(cur_node, map, leval + 1) node.add_child(cur_node, i) else: return features_name = [name for name in self.x] # 逆序 features_index = self.gain.argsort()[::-1] features_map = {} # 將資訊增益與對應的排名組成字典 for i,key in enumerate(features_index): features_map[i] = features_name[key] root = TreeNode(features_map[0]) dfs(root, features_map) return root # 後剪枝 def post_pruning(self,tree_dict,data,key=None): def processing_data(data,col_name,value): inx=data[col_name]==value return data[inx] for k in tree_dict: # 如果不是葉子節點 if not isinstance(tree_dict[k], str): if key in self.data.columns: # 遞迴遍歷所有節點 flag, count = self.post_pruning(tree_dict[k],data=processing_data(data,key,k),key=k) else:flag, count = self.post_pruning(tree_dict[k], data=data, key=k) # 如果知道葉子節點可以合併,返回兩次找到爺爺節點,把父節點變為save或not save if count == 1: return flag, count + 1 elif count == 2: tree_dict[k] = flag #葉子節點,判斷資料是否大於閾值 elif data.shape[0]<self.num_threshold: if len(data[data[self.target]==0])>=len(data[self.target])/2: return "not save",1 else:return "save",1 # 葉子節點,判斷是否都相同 elif np.array([v == "save" for v in tree_dict.values()]).all(): return "save", 1 elif np.array([v == "not save" for v in tree_dict.values()]).all(): return "not save", 1 continue return tree_dict, 0 def evaluator(self,tree_dict, test_data: "pd", target_name): #調換資料順序,按照資訊增益由大到小 columns=test_data.columns new_columns=[columns[i] for i in self.gain.argsort()[::-1]] new_columns.append(target_name) #改變順序 test_data=test_data.reindex(columns=new_columns) right=0 #遍歷test_data中每一行資料 for index,row in test_data.iterrows(): temp_tree = tree_dict #根據test_data做選擇 for name in new_columns: choice=row[name] #如果沒有當前分支則跳過 if choice not in temp_tree[name].keys(): value=None break value=temp_tree[name][choice] temp_tree=value if value in["save","not save"]: #將y和pred_y同一 value=0 if value=="not save" else 1 break if value==row[target_name]: right+=1 accuracy = right/len(test_data) return accuracy def createPlot(inTree): fig = plt.figure(1, facecolor='white') fig.clf() axprops = dict(xticks=[], yticks=[]) createPlot.ax1 = plt.subplot(111, frameon=False) # no ticks plotTree.totalW = float(getNumLeafs(inTree)) plotTree.totalD = float(getTreeDepth(inTree)) plotTree.xOff = -0.5 / plotTree.totalW plotTree.yOff = 1.0 plotTree(inTree, (0.5, 1.0), '') plt.show() class DataLoader(object): def __init__(self,data:"pd",random_seed=None,test_size=0.33): self.data=data self.test_size=test_size self.random_seed=random_seed if random_seed is not None else None def __getitem__(self, index): return self.data.iloc[index,:] def __len__(self): return len(self.data) def split_data(self): if self.random_seed is not None: np.random.seed(self.random_seed) train_data_idx=np.random.randint(0,len(self.data),size=int(len(self.data)*(1-self.test_size))) test_data_idx=np.random.randint(0,len(self.data),size=int(len(self.data)*self.test_size)) train_data=self.data.iloc[train_data_idx,:] test_data=self.data.iloc[test_data_idx,:] return train_data,test_data if __name__=="__main__": train_file = "D:/DataSet/titanic/titanic_train.csv" test_file = "D:/DataSet/titanic/titanic_test.csv" # 資料讀取 data = pd.read_csv(train_file) # test = pd.read_csv(test_file) data=process_data(data) target_name="Survived" target = data[target_name] #總的資訊熵 total_entropy = entropy(np.array(target)) #連續值處理 data = process_continue_value(data, target, total_entropy) #資料載入器 dataloader=DataLoader(data,random_seed=1) train_data,test_data=dataloader.split_data() #獲得資訊增益 gain=gain(total_entropy, train_data.drop(target_name,axis=1), target) #構造樹,設定樹的最大深度,每一個節點最少資料量等引數 tree=DecisionTree(np.array(gain),train_data,"Survived",num_threshold=10) root=tree.init() #獲得書的字典,為後續畫圖,剪枝準備 tree_dict = root.get_tree_dict(root,tree.data ) #後剪枝 for i in range(3): tree_dict=tree.post_pruning(tree_dict,tree.data)[0] # 模型評估 accuracy = tree.evaluator(tree_dict, test_data, target_name) print(accuracy) #plt作圖 createPlot(tree_dict) # print(tree_dict)