【影象處理筆記】特徵提取之整體影象特徵(Harris角點,MSER)
0 引言
特徵提取之邊界特徵和特徵提取之區域特徵兩篇部落格介紹的描述子非常適合於某些應用(如工業檢測),在這些應用中,可以使用影象分割中的方法可靠地分割影象中的各個區域。主分量特徵向量與前面的內容是不同的, 因為它們基於多幅影象。在某些應用中,如搜尋影象資料庫尋找匹配(如臉部辨識),影象之間的變化非常廣泛,因此這些方法都不再適用。本節將討論兩種解決這一問題的特徵檢測方法:(1)基於角的檢測(2)處理影象中的所有區域。

1 哈里斯-斯蒂芬斯角檢測器
1.1 原理及實現
我們直觀的認為角是曲線方向的快速變化。角是高度有效的特徵,因為它們對視點是獨特且合理不變的。由於這些特性,角在諸如自動導航跟蹤、立體機器視覺演演算法和影象資料庫查詢等應用中頻繁用於匹配影象特徵。
最常用的角點定義時Harris提出的,這些角點被稱為「哈爾角點」,可以被認為是原始的關鍵點。它們的定義依賴於一個區域中的畫素的自相關概念。簡單來說,這意味著「如果影象被移動了少量(Δx,Δy)位置,它與原來的自己有多相似?」
哈爾從以下自相關函數開始計算,令f表示影象,並令f(s,t)表示由(s,t)的值定義的一小塊影象。尺寸相同但移動了(x,y)的小塊影象是f(s+x,t+y)。於是,兩幅小塊影象的差的平方的加權和為

式中,w(s,t)是一個後面很快就要討論的加權函數。位移後的小塊影象可以用泰勒級數展開的線性項來近似:
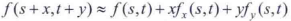
式中,fx(s,t)=df/dx和fy(s,t)=df/dy,它們都在(s,t)處計算。於是,上式可寫為

用矩陣形式可寫為

式中,

矩陣M是自相關矩陣。它的各項是在(s,t)處計算的。如果w(s,t)是各向同性的,那麼M是對稱的,因為A是對稱的。在HS檢測器中使用的加權函數w(s,t)通常有兩種形式:(1)在小塊影象內為1,在其他位置為0(即它的形狀類似盒式低通濾波器核);(2)指數形式,高斯加權,使靠近視窗中心的平方差比裡中心更遠的平方差的權重更大。當計算速度很快且噪音電平較低時,使用盒式核;資料平滑很重要時,使用指數函數。根據哈爾的定義,角點是影象中的自相關矩陣具有兩個大的特徵值的位置。實質上,這意味著在任何方向移動一小段距離都會造成影象改變。這種看待事物的有點在於,當我們只考慮自相關矩陣的特徵值時,我們考慮對旋轉不變的量,這很重要,因為我們正在跟蹤的物件可能會旋轉和轉換。
哈里斯-斯蒂芬斯(HS)角檢測器在影象上方移動一個小窗來檢測灰度變化,像空間濾波那樣。我們感興趣的是三個場景,
(1)各個方向上零(或小)灰度變化的區域,這發生在檢測器窗位於一個恆定(或幾乎恆定)區域時,如位置A所示;
(2)在某個方向上變化但在其正交方向上不變化的區域,這發生在檢測器視窗橫跨兩個區域之間的邊界時,如位置B所示;
(3)所有方向發生重大變化的區域,這發生在檢測器視窗包含一個角(或孤立點)時,如位置C所示。HS角檢測器是試圖區分這三個條件的數學公式。
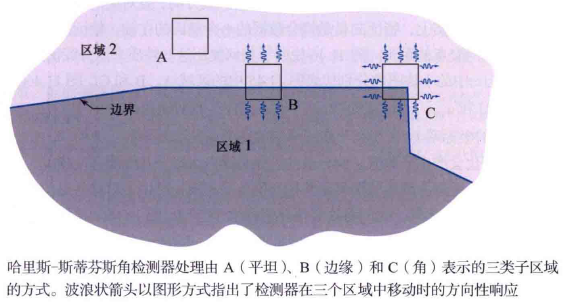
實對稱矩陣(如M)的特徵向量指向最大的資料拓展方向,且對應的特徵值與特徵向量方向上的資料拓展成正比。事實上,特徵向量是擬合資料的一個橢圓的主軸,特徵值的幅度是從這個橢圓的中心到橢圓與主軸的交點的距離。下面說明如何使用這些性質來區分我們感興趣的三種情況。
1. 求導:使用導數核wy=[-1 0 1]和wx=wyT計算(fx,fy)值。
2. 導數聚類:由於在小塊影象中的每個點處計算導數時,噪聲引起的變化會產生分散值,而分散的擴充套件與噪聲水平及其性質直接相關。
- 平坦區域的導數形成了一個近似為圓形的聚類,其特徵值幾乎相同,產生了對這些點的一個近乎圓形的擬合。
- 包含邊緣的小塊影象的導數,沿x軸的擴充套件更大,沿y軸的擴充套件和平坦區域的幾乎相同。於是兩個特徵值一個大一個小。擬合資料的橢圓在x方向拉長了。
- 包含角的小塊影象的導數資料沿兩個方向擴充套件,得到兩個大特徵值和一個大得多的幾乎為圓形的擬合橢圓。
因此得出結論:(1)兩個小特徵值表示幾乎恆定的灰度;(2)一個小特徵值和一個大特徵值表示存在垂直邊界或水平邊界;(3)兩個大特徵值表示存在一個角或孤立的亮點。因此我們可以用小塊影象中由導數形成的矩陣的特徵值來區分三種感興趣的場景。
3. 角響應測度:由於特徵值計算開銷大,HS檢測器使用了角響應測度。我們知道,一個平方矩陣的積等於該矩陣的特徵值之和,該矩陣的行列式等於其特徵值的積,角響應測度就是基於此,定義為
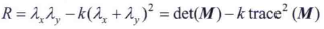
式中,k是一個常數,根據經驗確定,預設為0.04。可以將k是為一個敏感因子,k越小,檢測器越有可能找到角。當兩個特徵值都較大時,測度R具有較大正值,這表示存在一個角;一個特徵值較大而另一個特徵值較小時,測度R具有較小的負值;兩個特徵值都較小時,測度R的絕對值較小,表明小塊影象時平坦的。R通常結合一個閾值T使用。當小塊影象的R>T那麼在小塊影象中檢測到了一個角。
範例 演演算法實現
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main() {
Mat src = imread("./12.bmp", 0);
Mat markImg = imread("./12.bmp");
Mat kx = (Mat_<float>(1, 3) << -1, 0, 1);
Mat ky = (Mat_<float>(3, 1) << -1, 0, 1);
vector<Rect> rects = { Rect(2225,350,30,30), Rect(2225,405,30,30), Rect(2190,405,30,30) };
for (int i = 0; i < rects.size(); i++) {
rectangle(markImg, rects[i], Scalar(0, 255, 0), 1);
Mat roi = src(rects[i]);//從一張圖上裁的三個區域
Mat mask = Mat::zeros(Size(500, 500), CV_8UC1);
Mat fx, fy;
filter2D(roi, fx, CV_32F, kx);
filter2D(roi, fy, CV_32F, ky);
vector<Point> points;
for (int i = 0; i < 30; i++) {
for (int j = 0; j < 30; j++) {
Point p = Point(fx.at<float>(i, j), fy.at<float>(i, j));
Point p_offset = p + Point(250, 250);
mask.at<uchar>(p_offset.y, p_offset.x) = 255;
points.push_back(p_offset);
}
}
Mat M = Mat::zeros(Size(2, 2), CV_32FC1);
fx /= Scalar::all(255);
fy /= Scalar::all(255);
Mat q1, q2, q3;
multiply(fx, fx, q1);
multiply(fx, fy, q2);
multiply(fy, fy, q3);
M.at<float>(0, 0) = sum(sum(q1))[0];
M.at<float>(0, 1) = sum(sum(q2))[0];
M.at<float>(1, 0) = sum(sum(q2))[0];
M.at<float>(1, 1) = sum(sum(q3))[0];
Mat values;
eigen(M, values);
cout << "lamda1:" << values.ptr<float>(0)[0] << ", lamda2:" << values.ptr<float>(1)[0];
double R = determinant(M) - 0.04 * pow(trace(M)[0], 2);
cout << ", R:" << R << endl;
imshow("roi"+to_string(i), roi);
imshow("mask" + to_string(i), mask);
}
waitKey(0);
return 0;
}

1.2 OpenCV中的Harris角檢測器
OpenCV 中提供了 Harris 角點檢測函數cv::cornerHarris()。
void cornerHarris( InputArray src, //輸入影象,單通道的8位元影象或浮點數影象
OutputArray dst, //輸出影象,Harris檢測器的響應,大小與src相同,格式為CV_32FC1
int blockSize,//鄰域尺寸 int ksize, //Sobel運算元的核大小
double k,//Harris檢測器調節引數,通常取0.04-0.06 int borderType = BORDER_DEFAULT );//邊界擴充型別
OpenCV函數cv::cornerSubPix()用於細化角點位置,以亞畫素精度檢測到角點位置.不僅可以用於對 Harris 角點檢測結果進行細化檢測,也可以用於對其它角點檢測結果進行細化檢測。
void cornerSubPix( InputArray image,
InputOutputArray corners, Size winSize,
Size zeroZone, TermCriteria criteria );
範例 標定板找角點
下面的標定板過渡畫素比較多,我們先找到Harris角,然後通過角(一些畫素)的中心來細化它們。
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main() {
Mat src = imread("./13.bmp", 0);
Mat markImg = imread("./13.bmp");
imshow("src", markImg);
Mat dst, binImg;
cornerHarris(src, dst, 5, 9, 0.04);
normalize(dst, dst, 0, 1.0, NORM_MINMAX);
threshold(dst, binImg, 0.25, 1, THRESH_BINARY);
binImg.convertTo(binImg, CV_8U, 255);
vector<vector<Point>> contours;
findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
vector<Point2f> corners;
for (size_t i = 0; i < contours.size(); i++)
{
Point2f center; float radius;
minEnclosingCircle(contours[i], center, radius);
if(radius>2)
corners.push_back(center);
}
TermCriteria criteria = TermCriteria(TermCriteria::EPS + TermCriteria::MAX_ITER, 1000, 0.001);
cornerSubPix(src, corners, cv::Size(7, 7), cv::Size(-1, -1), criteria);
for (size_t i = 0; i < corners.size(); i++)
circle(markImg, corners[i], 3, Scalar(0, 255, 0), 3);
imshow("markImg", markImg);
waitKey(0);
return 0;
}

2 最大穩定極值區域(MSER)
2.1 原理
上節討論的哈里斯-斯蒂芬斯(HS)角檢測器在由灰度的急劇過渡(如直邊緣的交點,它在影象中會導致類似角的特徵)表徵的應用中是有用的。相反,Matas et al.[2002]提出的最大穩定極值區域(MSER)面向的更多的是「斑點」。像HS角檢測器那樣,MSER通常會產生整體影象特徵,以便在兩幅或多幅影象之間建立對應關係。
MSER演演算法是主要是基於分水嶺的思想進行檢測,其過程是:對一幅灰度影象取不同的閾值進行二值化處理,閾值從0至255遞增,這個遞增的過程就好比是一片土地上的水面不斷上升,隨著水位的不斷上升,一些較低的區域就會逐漸被淹沒,從天空鳥瞰,大地變為陸地、水域兩部分,並且水域部分在不斷擴大。在這個「漫水」的過程中,影象中的某些連通區域變化很小,甚至沒有變化,則該區域就被稱為最大穩定極值區域。
上面的過程可以轉換為有根的連通樹,它成為分量數。這棵樹的每個節點表示一個極值區域,分析分量數的節點可以求出MSER。對於樹中的每個連通區域,我們計算一個穩定性測度,定義為
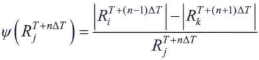
式中,|R|是連通區域R的面積(畫素數量),T是值域T∈[min(I), max(I)]內的一個閾值,ΔT是一個規定的閾值增量Ri,Rj,R是不同閾值得到的連通區域。MSER是分量數中的一個節點區域,該節點在該路徑上具有區域性極小的一個穩定值。可能有點難以理解,舉個栗子,下面的影象灰度區間為[5,225],取閾值T=10,ΔT=50對影象的不同區域進行分割。左邊一列是閾值處理後的結果,右邊是分量數。注意,數的根朝上。下圖只有一個MSER。

2.2 OpenCV中的MSER
cv::MSER類的範例可以通過create方法建立。在初始化時指定被檢測區域的最小和最大尺寸,以便限制被檢測特徵的數量。
Ptr<MSER> create( int delta=5, //允許灰度閾值的最小變化步長,即一次灰度值增加的量,取值範圍(0,160),預設為5
int min_area=60, //允許區域最小的面積
int max_area=14400,//允許區域最大的面積 double max_variation=0.25, //允許不同強度閾值下的區域之間的最大面積變化率,取值範圍為(0,1),越接近1,則越多區域被認為是穩定的,如果接近0,則只能找到非常少的穩定區域,預設為0.25
double min_diversity=.2,//對於彩色影象,回溯以切斷多樣性小於 min_diversity 的 mser int max_evolution=200, //對於彩色影象,進化步驟
double area_threshold=1.01,//對於彩色影象,導致重新初始化的區域閾值 double min_margin=0.003, //對於彩色影象,忽略太小的邊距
int edge_blur_size=5 );//對於彩色影象,邊緣模糊的光圈大小
可以通過呼叫 detectRegions 方法來獲得 MSER,指定輸入影象和一個相關的輸出資料結構
void detectRegions( InputArray image,//輸入影象可以是灰度圖或者灰度圖的梯度圖 std::vector<std::vector<Point> >& msers,//mser區域用點表示 std::vector<Rect>& bboxes ) = 0;//mser區域用rect表示
範例 利用MSER提取文字區域
書上的例子有點抽象,我搜了下,MSER在傳統OCR中應用較廣,是一個較為流行的文字檢測傳統方法(相對於基於深度學習的AI文字檢測而言)。在一幅有文字的影象上,文字區域由於顏色(灰度值)是一致的,因此在水平面(閾值)持續增長的過程中,一開始不會被「淹沒」,直到閾值增加到文字本身的灰度值時才會被「淹沒」。該演演算法可以用來粗略地定位出影象中的文字區域位置。我找了張圖試了下,效果不錯,但是那張圖直接做閾值分割+查詢輪廓也能得到一樣的效果。所以我又找了一張車牌,唔,有點東西。
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
bool cmp(Rect r1, Rect r2) {
return r1.x < r2.x;
}
float IOU(const Rect& box1, const Rect& box2)
{
if (box1.x > box2.x + box2.width) { return 0.0; }
if (box1.y > box2.y + box2.height) { return 0.0; }
if (box1.x + box1.width < box2.x) { return 0.0; }
if (box1.y + box1.height < box2.y) { return 0.0; }
float colInt = min(box1.x + box1.width, box2.x + box2.width) - max(box1.x, box2.x);
float rowInt = min(box1.y + box1.height, box2.y + box2.height) - max(box1.y, box2.y);
float intersection = colInt * rowInt;
float area1 = box1.width * box1.height;
float area2 = box2.width * box2.height;
return intersection / (area1 + area2 - intersection);
}
vector<Rect> nms(vector<Rect> boxes, double overlapThreshold) {
sort(boxes.begin(), boxes.end(), cmp); //將矩形框排序
Rect r = boxes[0];
vector<Rect> boxes_selectes = { r };
int i = 1;
while (i < boxes.size()) {
if (!(IOU(r, boxes[i]) > overlapThreshold)) {//計算交併比
boxes_selectes.push_back(boxes[i]);
r = boxes[i];
}
i++;
}
return boxes_selectes;
}
int main() {
Mat src = imread("./1.jpg", 0);
Mat markImg = imread("./1.jpg");
imshow("src", markImg);
vector<vector<Point> > points;
vector<Rect> rects;
Ptr<MSER> ptrMSER = MSER::create(1, 50, 10000);
ptrMSER->detectRegions(src, points, rects);
// 根據文字的大小篩選
vector<Rect> boxes;
for (int i = 0; i < rects.size(); i++) {
if (rects[i].width < 60 && rects[i].height>60)
boxes.push_back(rects[i]);
}
// 非極大值抑制
vector<Rect> boxes_selectes = nms(boxes, 0.1);
for (int i = 0; i < boxes_selectes.size(); i++)
rectangle(markImg, boxes_selectes[i], Scalar(0, 255, 0), 1);
imshow("markImg", markImg);
waitKey(0);
return 0;
}


參考:
1. 岡薩雷斯《數位影像處理(第四版)》Chapter 11(所有圖片可在連結中下載)
2. 深度學習文字定位