1、場景描述

1.1 需求

  假設，我們有三臺快取伺服器，有3萬張圖片需要快取，希望這些圖片被均勻的快取到這3臺伺服器上，以便它們能夠分攤快取的壓力，即我們希望每臺伺服器能夠快取1萬張左右圖片，那麼，我們應該怎樣做呢？

1.2 方法

  如果我們無規律地將3萬張圖片平均的快取在3臺伺服器上，雖然可以滿足我們的需求，但是如果這樣做，當我們需要存取某個快取項時，則需要遍歷3臺快取伺服器，從3萬個快取項中找到我們需要存取的快取，遍歷的過程效率太低，時間太長，也就失去了快取的意義，快取的目的就是提高速度，改善使用者體驗，減輕後端伺服器壓力，如果每次讀取一個快取，都需要遍歷所有快取伺服器所有快取項，想想就覺得很累，那麼，我們該怎麼辦呢？

  原始的做法是對快取項的鍵進行雜湊，將hash後的結果對快取伺服器的數量進行取模操作，通過取模後的結果，決定快取項將會快取在哪一臺伺服器上，以剛才描述的場景為例，假設我們使用圖片名稱作為存取圖片的key，假設圖片名稱是不重複的，那麼，我們可以使用公式：hash（圖片名稱）% N，計算出圖片應該存放在哪臺伺服器上。
  因為圖片的名稱是不重複的，所以，當我們對同一個圖片名稱做相同的雜湊計算時，得出的結果應該是不變的，如果我們有3臺伺服器，使用雜湊後的結果對3求餘，那麼餘數一定是0、1或者2，如果求餘的結果為0， 我們就把當前圖片名稱對應的圖片快取在0號伺服器上，如果餘數為1，就把當前圖片名對應的圖片快取在1號伺服器上，如果餘數為2，同理。那麼，當我們存取任意一個圖片的時候，只要再次對圖片名稱進行上述運算，即可得出對應的圖片應該存放在哪一臺快取伺服器上，我們只要在這一臺伺服器上查詢圖片即可，如果圖片在對應的伺服器上不存在，則證明對應的圖片沒有被快取，也不用再去遍歷其他快取伺服器了
  通過這樣的方法，即可將3萬張圖片隨機的分佈到3臺快取伺服器上了，而且下次存取某張圖片時，直接能夠判斷出該圖片應該存在於哪臺快取伺服器上，這樣就能滿足我們的需求了，我們暫時稱上述演演算法為HASH取模演演算法，過程可以用下圖表示：

  但是，使用上述HASH演演算法進行快取時，會不會有缺陷？

  如果3臺快取伺服器無法滿足我們的快取需求，那麼我們應該怎麼做呢？沒錯，很簡單，增加伺服器，假設我們增加了一臺快取伺服器，那麼快取伺服器的數量就由3臺變成了4臺，此時，如果仍然使用上述方法對同一張圖片進行快取，那麼這張圖片所在的伺服器編號必定與原來3臺伺服器時所在的伺服器編號不同，因為除數由3變為了4，被除數不變的情況下，餘數肯定不同，這種情況帶來的結果就是當伺服器數量變動時，所有快取的位置都要發生改變，所有快取在一定時間內是失效的，當應用無法從快取中獲取資料時，則會向後端伺服器請求資料，
  同理，假設3臺快取中突然有一臺快取伺服器出現了故障，無法進行快取，那麼我們則需要將故障機器移除，但是如果移除了一臺快取伺服器，那麼快取伺服器數量從3臺變為2臺，如果想要存取一張圖片，這張圖片的快取位置必定會發生改變，以前快取的圖片也會失去快取的作用與意義，由於大量快取在同一時間失效，造成了快取的雪崩，此時前端快取已經無法起到承擔部分壓力的作用，後端伺服器將會承受巨大的壓力，整個系統很有可能被壓垮。

  使用上述HASH演演算法會出現的問題：當快取伺服器數量發生變化時，會引起快取的雪崩，可能會引起整體系統壓力過大而崩潰（大量快取同一時間失效），為了解決這些問題，一致性雜湊演演算法誕生了。

2、基本概念

​  一致性雜湊演演算法實際也是取模演演算法，只是前面描述的取模演演算法是對伺服器的數量進行取模，而一致性雜湊演演算法是對2^32取模。

2.1hash環

  我們可以把2^32 想象成一個圓，就像鐘錶一樣，鐘錶是由60個點組成的圓，此處我們把這個圓想象成由2^32個點組成的圓，示意圖如下：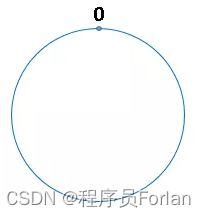

  圓環的正上方的點代表0，0點右側的第一個點代表1，以此類推，2、3、4、5、6……直到2^32-1 ,0點左側的第一個點代表2^32-1 ，我們把這個由2^32 個點組成的圓環稱為hash環。

2.2 原理

  以之前描述的場景為例，假設我們有3臺快取伺服器，伺服器A、伺服器B、伺服器C，用它們各自的IP地址進行雜湊計算，使用雜湊後的結果對2^32取模，公式如下：
（1）hash（伺服器A的IP地址） % 2^32
（2）hash（伺服器B的IP地址） % 2^32
（3）hash（伺服器C的IP地址） % 2^32
  通過上述公式算出的結果一定分別是一個0到2^32-1 之間的一個整數，使用這個整數代表伺服器，伺服器就可以對映到這個環上，假設3臺伺服器對映到hash環上，如下圖：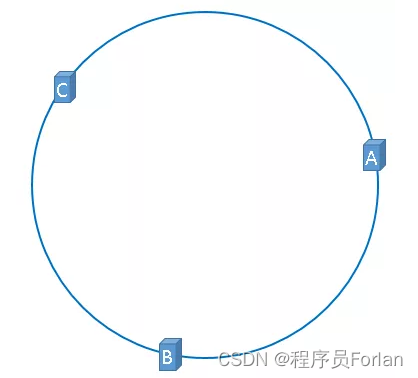

  通過上述方法，把快取伺服器對映到了hash環上，使用同樣的方法，將需要快取的物件對映到hash環上。
  假設，我們需要使用快取伺服器快取圖片，使用圖片的名稱作為找到圖片的key，公式：hash（圖片名稱） % 2^32，將圖片對映到上圖中的hash環上，對映後的示意圖如下，圖中的橘黃色圓形就表示圖片：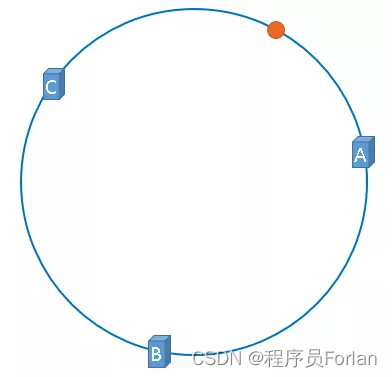

  伺服器與圖片都被對映到了hash環上，那麼上圖中的這個圖片到底應該被快取到哪一臺伺服器上呢？
  上圖中的圖片將會被快取到伺服器A上，因為從圖片的位置開始，沿順時針方向遇到的第一個伺服器就是快取點，即A伺服器，所以，上圖中的圖片將會被快取到伺服器A上，如下圖所示：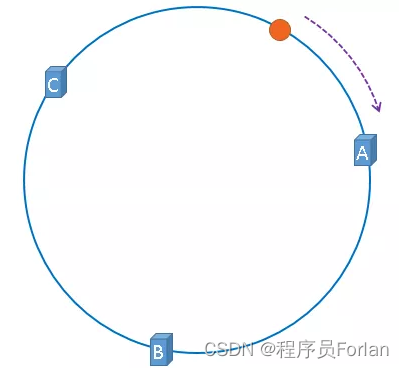

  一致性雜湊演演算法就是通過這種方法，判斷一個物件應該被快取到哪臺伺服器上的，快取伺服器與被快取物件都對映到hash環上以後，從被快取物件的位置出發，沿順時針方向遇到的第一個伺服器，就是當前物件將要快取於的伺服器，由於被快取物件與伺服器hash後的值是固定的，所以，在伺服器不變的情況下，一張圖片必定會被快取到固定的伺服器上，當下次想要存取這張圖片時，只要再次使用相同的演演算法進行計算，即可算出這個圖片被快取在哪個伺服器上，直接去對應的伺服器查詢對應的圖片即可。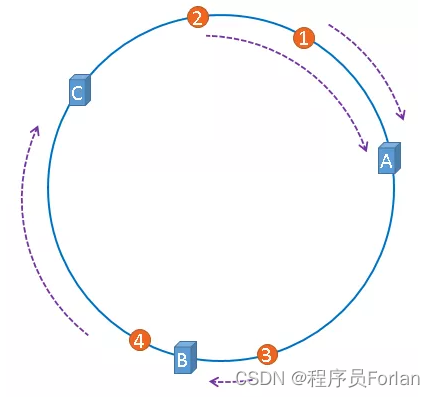

  假設有四張圖片需要快取，示意圖如上，1號、2號圖片將會被快取到伺服器A上，3號圖片將會被快取到伺服器B上，4號圖片將會被快取到伺服器C上。

3、優缺點分析

  如果只是簡單對伺服器數量取模，那麼當伺服器數量發生變化時，會產生快取的雪崩，從而很有可能導致系統崩潰，那麼使用一致性雜湊演演算法，能夠避免這個問題嗎？
  假設，伺服器B出現了故障，我們現在需要將伺服器B移除，那麼，我們將上圖中的伺服器B從hash環上移除即可，移除伺服器B以後示意圖如下：

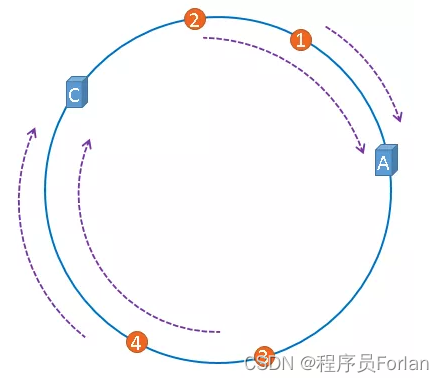
  在伺服器B未移除時，圖片3應該被快取到伺服器B中，當伺服器B移除以後，按照一致性雜湊演演算法的規則，圖片3應該被快取到伺服器C中，因為從圖片3的位置出發，沿順時針方向遇到的第一個快取伺服器節點就是伺服器C，也就是說，如果伺服器B出現故障被移除時，圖片3的快取位置會發生改變。
  但是，圖片4仍然會被快取到伺服器C中，圖片1與圖片2仍然會被快取到伺服器A中，這與伺服器B移除之前並沒有任何區別，這就是一致性雜湊演演算法的優點，即伺服器的數量如果發生改變，並不是所有快取都會失效，而是隻有部分快取會失效，它並不能杜絕資料遷移的問題，但是可以有效避免資料的全量遷移，需要遷移的只是被移除節點和它上游節點（逆時針最近一個）之間的那部分資料。

4、資料傾斜

在介紹一致性雜湊的概念時，我們理想化的將3臺伺服器均勻的對映到了hash環上，如下圖所示：

在實際的對映中，伺服器可能會被對映成如下模樣：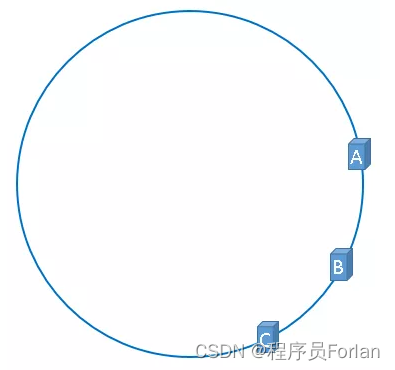

如果伺服器被對映成上圖中的模樣，那麼被快取的物件很有可能大部分集中快取在某一臺伺服器上，如下圖所示：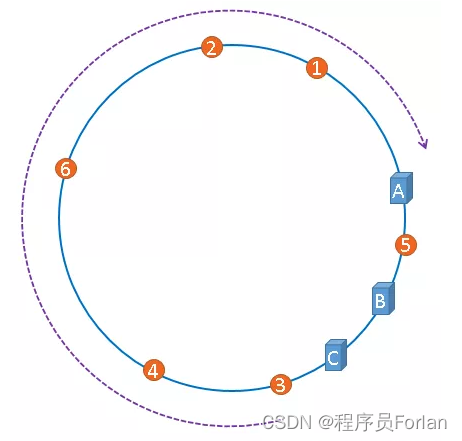

  上圖中，1號、2號、3號、4號、6號圖片均被快取在了伺服器A上，只有5號圖片被快取在了伺服器B上，伺服器C上甚至沒有快取任何圖片，如果出現上圖中的情況，A、B、C三臺伺服器並沒有被合理的平均的充分利用，快取分佈的極度不均勻，而且，如果此時伺服器A出現故障，那麼失效快取的數量也將達到最大值，在極端情況下，仍然有可能引起系統的崩潰，上圖中的情況被稱為資料傾斜，那麼，我們應該怎樣防止資料傾斜呢？
  那就是加入虛擬節點。

5、虛擬節點

​ 由於我們只有3臺伺服器，當我們把伺服器對映到hash環上時，很有可能出現資料傾斜的情況，快取往往會極度不均衡的分佈在各伺服器上，如果想要均衡的將快取分佈在3臺伺服器上，最好能讓這3臺伺服器儘量多的、均勻的出現在hash環上，但是，真實的伺服器資源只有3臺，我們怎樣憑空的讓它們多起來呢，沒錯，就是憑空的讓伺服器節點多起來，既然沒有多餘的真正的物理伺服器節點，我們就只能將現有的物理節點通過虛擬的方法複製出來，這些由實際節點虛擬複製而來的節點被稱為"虛擬節點"。加入虛擬節點以後的hash環如下：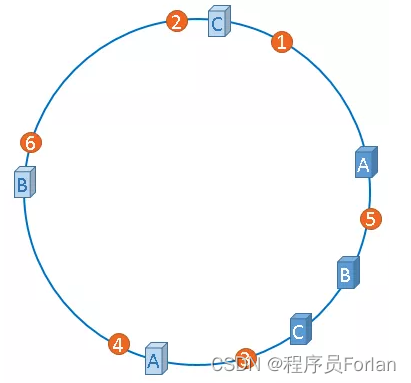

  虛擬節點是物理節點（實際的物理伺服器）在hash環上的複製品,一個實際節點可以對應多個虛擬節點
  ​從上圖可以看出，A、B、C三臺伺服器分別虛擬出了一個虛擬節點，如果你需要，也可以虛擬出更多的虛擬節點。
  引入虛擬節點的概念後，快取的分佈就均衡多了，上圖中，1號、3號圖片被快取在伺服器A中，5號、4號圖片被快取在伺服器B中，6號、2號圖片被快取在伺服器C中。
  如果你還不放心，可以虛擬出更多的虛擬節點，以便減小資料傾斜所帶來的影響，虛擬節點越多，hash環上的節點就越多，快取被均勻分佈的概率就越大。

6、補充總結說明

6.1 虛擬節點設定多少個？

沒有必要全部設定成虛擬節點，根據測試結果，看看多少個的效果最好，實現比較均勻

6.2 新加節點，造成部分舊資料無法命中，怎麼處理？

原因：新加節點時，獲取資料從新新節點獲取，但資料還在後面舊節點，還沒遷移完成。
解決：獲取資料時，可以從順時針最近的兩個節點取，取不到再從資料庫獲取，會增加複雜度，看場景做取捨。

6.3 一致性hash演演算法原理

node和data都參與計算，對映到hash環上，node先進行hash得到對映點，新增data時，data進行hash得到數值，找距離最近的node點。