如何使用分治演演算法的思想,分治技巧詳解
分治演演算法
分治演演算法的思想
分治演演算法(divide and conquer)的核心思想其實就是四個字,分而治之 ,也就是將原問題劃分成n個規模較小,並且結構與原問題相似的子問題,遞迴地解決這些子問題,然後再合併其結果,就得到原問題的解。
分治演演算法和遞迴的區別
分治是處理問題的思想,遞迴是一種程式設計技巧。分治一般都比較適合用用遞回來實現。
分治演演算法的實現中,每一層地遞迴都會涉及到下面三個操作:
分解:將原問題分解成一系列子問題;
解決:將子問題的結果合併成原問題。
使用分治演演算法需要滿足的條件
1、原問題與分解成的小問題具有相同的模式;
2、原問題分解成的子問題可以獨立求解,子問題之間沒有相關性;
3、具有分解終止條件,也就是說,當問題足夠小時,可以直接求解;
4、可以將子問題合併成原問題,而這個合併操作的複雜度不能太高,否則就起不到減小演演算法總體複雜度的效果了。
經典題目
1、二分搜尋
給定一個n個元素有序的(升序)整型陣列nums 和一個目標值target ,寫一個函數搜尋nums中的 target,如果目標值存在返回下標,否則返回 -1。
範例 1:
輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中並且下標為 4
範例2:
輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1
題目連結:https://leetcode.cn/problems/binary-search
解題思路
1、滿足分支演演算法的思想,將為題分解為規模較小的相同問題時,就比較容易求解;
2、找出中間的值和目標值進行比較,通過判斷大小,來不斷的縮小問題的求解範圍;
3、這樣每次的求解,總是能將問題的範圍縮小一半,或者找出目標值。
時間複雜度:O(logn)
空間複雜度:O(1)
func search(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := (right + left) / 2
if nums[mid] == target {
return mid
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] < target {
left = mid + 1
}
}
return -1
}
2、第一個錯誤的版本
你是產品經理,目前正在帶領一個團隊開發新的產品。不幸的是,你的產品的最新版本沒有通過質量檢測。由於每個版本都是基於之前的版本開發的,所以錯誤的版本之後的所有版本都是錯的。
假設你有 n 個版本 [1, 2, ..., n],你想找出導致之後所有版本出錯的第一個錯誤的版本。
你可以通過呼叫bool isBadVersion(version)介面來判斷版本號 version 是否在單元測試中出錯。實現一個函數來查詢第一個錯誤的版本。你應該儘量減少對呼叫 API 的次數。
範例 1:
輸入:n = 5, bad = 4
輸出:4
解釋:
呼叫 isBadVersion(3) -> false
呼叫 isBadVersion(5)-> true
呼叫 isBadVersion(4)-> true
所以,4 是第一個錯誤的版本。
範例 2:
輸入:n = 1, bad = 1
輸出:1
連結:https://leetcode.cn/problems/first-bad-version
題解:
這道題目是二分查詢的變種題目,找出最近的一個出錯的版本,也就是出錯版本的左邊都是出錯的版本;
所以利用二分查詢,找出出錯的又邊界即可
/**
* Forward declaration of isBadVersion API.
* @param version your guess about first bad version
* @return true if current version is bad
* false if current version is good
* func isBadVersion(version int) bool;
*/
func firstBadVersion(n int) int {
left, right := 0, n
for left < right {
mid := (right + left) / 2
if isBadVersion(mid) {
right = mid
} else {
left = mid + 1
}
}
return right
}
// 測試函數
func isBadVersion(n int) bool {
return false
}
3、快速排序
快速排序在我們剛學習演演算法的時候就遇到了過了,其中它使用到的演演算法思想就是分治策略。
它的處理思路就是,會選中一個基準數,通過一趟排序,和當前的基準數進行比較,將資料分總成兩部分,一部分大於基準數,另一部分小於基準數。
然後對這兩部分資料在進行上面的操作,直到所有的資料都有序,整個排序的過程可以使用遞回去實現。
快排的時間複雜度:平均情況下快速排序的時間複雜度是Θ(nlgn),最壞情況是n2
空間複雜度:最好空間複雜度為 O(logn),最壞空間複雜度為 O(n)
上程式碼
func QuickSort(arr []int) {
quickSort(arr, 0, len(arr)-1)
}
func quickSort(data []int, l, u int) {
if l < u {
m := partition(data, l, u)
quickSort(data, l, m-1)
quickSort(data, m, u)
}
}
func partition(data []int, l, u int) int {
quick := data[l]
left := l
for i := l + 1; i <= u; i++ {
if data[i] <= quick {
left++
data[left], data[i] = data[i], data[left]
}
}
data[l], data[left] = data[left], data[l]
return left + 1
}
4、歸併排序
歸併排序也是使用分治思想實現的一個比較經典的栗子,這裡來分析下
歸併排序的處理思路:
1、首先拆分子序列,使得子序列很容易排序,然後對子序列進行排序;
2、然後是合併的過程,將有序的子序列合併;
3、合併子序列的過程;
-
1、申請空間,大小為兩個已經排好序的子序列大小之和,該空間用來存放合併後的序列;
-
2、設定兩個指標,最初位置分別為兩個已經排序序列的起始位置;
-
3、比較兩個指標所指向的元素,選擇相對小的元素放入到合併空間,並移動指標到下一位置;
-
4、重複步驟3直到某一指標超出序列尾;
-
5、將剩下的元素直接複製到合併序列尾部;
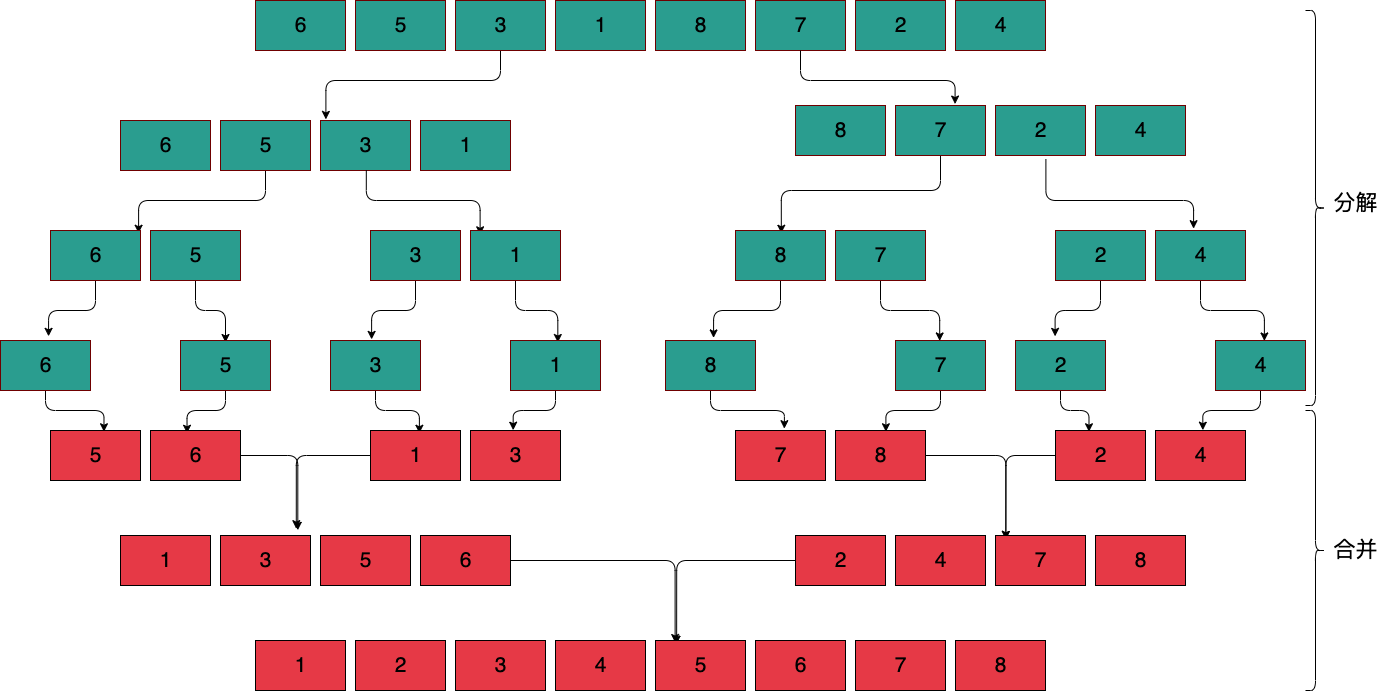
具體的動畫細節
上程式碼
時間複雜度 O(nlogn)
空間複雜度 O(n)
func MergeSort(arr []int) []int {
if len(arr) <= 1 {
return arr
}
mid := len(arr) / 2
leftArr := MergeSort(arr[0:mid])
rightArr := MergeSort(arr[mid:])
return merge(leftArr, rightArr)
}
func merge(left, right []int) []int {
i, j := 0, 0
m, n := len(left), len(right)
var result []int
// 合併子序列
for {
// 任何一個區間遍歷完成就退出
if i >= m || j >= n {
break
}
if left[i] > right[j] {
result = append(result, right[j])
j++
} else {
result = append(result, left[i])
i++
}
}
// 左邊的子集沒有遍歷完成,將左側的放入到結果集
if i < m {
result = append(result, left[i:]...)
}
// 右側的子集沒有遍歷完成,將右側的放入到結果集中
if j < n {
result = append(result, right[j:]...)
}
return result
}
直接在原陣列上進行操作
func MergeSort(nums []int) []int {
mergeSort(nums, 0, len(nums)-1)
return nums
}
func mergeSort(nums []int, start, end int) {
if start >= end {
return
}
mid := start + (end-start)/2
mergeSort(nums, start, mid)
mergeSort(nums, mid+1, end)
var tmp []int
i, j := start, mid+1
for i <= mid && j <= end {
if nums[i] > nums[j] {
tmp = append(tmp, nums[j])
j++
} else {
tmp = append(tmp, nums[i])
i++
}
}
if i <= mid {
tmp = append(tmp, nums[i:mid+1]...)
}
if j <= end {
tmp = append(tmp, nums[j:end+1]...)
}
for i := start; i <= end; i++ {
nums[i] = tmp[i-start]
}
}
5、陣列中的逆序對
題目地址:https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
在陣列中的兩個數位,如果前面一個數位大於後面的數位,則這兩個數位組成一個逆序對。輸入一個陣列,求出這個陣列中的逆序對的總數。
輸入: [7,5,6,4]
輸出: 5
解題思路
首先用到的是分治演演算法的思想
1、什麼是逆序對,就是前面的數位大小,小於位於其後面的數位大小,那麼這就是一個逆序對;
2、這裡主要用到了分治的演演算法,只是在分治演演算法的基礎之上,在進行資料的合併的時候,因為左邊部分和右邊部分都是已經排好序了,所以可以使用這種關係,來計算逆序對的個數;
3、具體的合併計算過程;
-
1、在左邊和右邊陣列中,都從第一個下標,開始匹配;
-
2、如果左邊當前下標的數大於右邊陣列當前下標的值,因為這兩個陣列都是從大到小排序的,所有左邊從當前下標開始數,都大於右邊當前匹配下標的數,
cnt += mid - i + 1,同時右邊陣列下標前移; -
3、如果左邊當前下標的數小於右邊陣列當前下標的值,不滿足,左邊陣列下標前移;
func reversePairs(nums []int) int {
return mergeSort(nums, 0, len(nums)-1)
}
func mergeSort(nums []int, start, end int) int {
if start >= end {
return 0
}
mid := start + (end-start)/2
cnt := mergeSort(nums, start, mid) + mergeSort(nums, mid+1, end)
tmp := []int{}
i, j := start, mid+1
for i <= mid && j <= end {
if nums[i] > nums[j] {
tmp = append(tmp, nums[j])
cnt += mid - i + 1
j++
} else {
tmp = append(tmp, nums[i])
i++
}
}
if i <= mid {
tmp = append(tmp, nums[i:mid+1]...)
}
if j <= end{
tmp = append(tmp, nums[j:end+1]...)
}
for i := start; i <= end; i++ {
nums[i] = tmp[i-start]
}
return cnt
}
6、漢諾塔
漢諾塔問題的描述:
假設有 A、B、C 三根柱子。其中在 A 柱子上,從下往上有 N 個從大到小疊放的盤子。我們的目標是,希望用盡可能少的移動次數,把所有的盤子由 A 柱移動到 C 柱。過程中,每次只能移動一個盤子,且在任何時候,大盤子都不可以在小盤子上面。
解題思路:
嘗試把問題分解,使用分治的思想,將問題分解成一個個容易解決的子問題,然後一個個的去解決
我們把一個 N 層漢諾塔從 A 搬到 C,我們假定只有兩層,首先把 N-1 層搬到 B,然後把下面的第 N 層搬到 C,然後再把 N-1 層從 B 搬到 C 。
如果存在多層,那我們就假定 N-1 層已經排好序了,只搬第 N 層,這樣依次遞迴下去。
終止條件:
當只剩下最後一個的時候,我們只需要搬動一次就行了
var count int = 0
func main() {
beadNum := 5 // This is the initial number of beads
hanoi(beadNum, "A", "B", "C")
fmt.Println(count)
}
func hanoi(beadNum int, pillarA string, pillarB string, pillarC string) {
if beadNum == 1 {
// 最後一個了,可以結束了
move(beadNum, pillarA, pillarC)
} else {
// Step 2: 將 N-1 層從 A 移動到 B
hanoi(beadNum-1, pillarA, pillarC, pillarB)
// Step 2: 將第 N 層從 A 移動到 C
move(beadNum, pillarA, pillarC)
// Step 3: 將 B 中的 N-1 層移動到 C
hanoi(beadNum-1, pillarB, pillarA, pillarC)
}
}
func move(beadNum int, pillarFrom string, pillarTo string) {
count += 1
}
總結
1、分治演演算法(divide and conquer)的核心思想其實就是四個字,分而治之 ,也就是將原問題劃分成n個規模較小,並且結構與原問題相似的子問題,遞迴地解決這些子問題,然後再合併其結果,就得到原問題的解。
2、分治是處理問題的思想,遞迴是一種程式設計技巧。分治一般都比較適合用用遞回來實現。
3、分治演演算法的實現中,每一層地遞迴都會涉及到下面三個操作:
-
分解:將原問題分解成一系列子問題;
-
解決:將子問題的結果合併成原問題。
參考
【資料結構與演演算法之美】https://time.geekbang.org/column/intro/100017301
【經典優化演演算法之分治法】https://zhuanlan.zhihu.com/p/45986027
【歸併排序】https://zh.m.wikipedia.org/zh-hans/歸併排序
【歸併排序】https://geekr.dev/posts/go-sorting-algorithm-merge
【分治使用技巧】https://boilingfrog.github.io/2022/11/17/分治演演算法的思想/