論人類下一代語言的可能—8.1圖靈機
除了在紙筆媒介系統下以書面符號形式進行數學計算外,從一開始我們也設計和製造計算工具,利用這些工具來進行數學計算。 現代計算機是計算工具的最新產品。上世紀三十年代,英國數學家圖靈(Alan Mathison Turing,1912.6-1954.6)提出了圖靈機的概念,其基本原理如下。
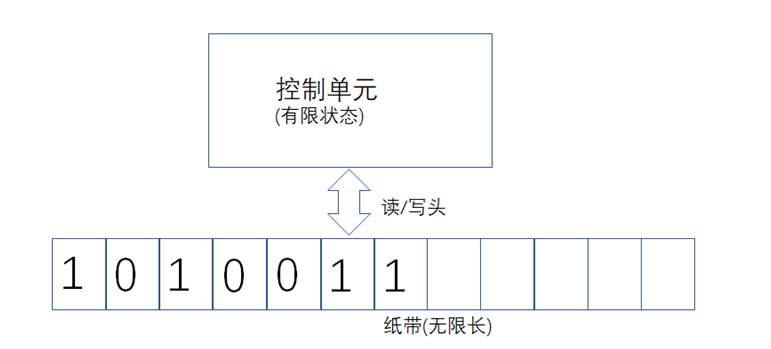
(圖8-1:圖靈機)
圖靈機的構成包括:
1紙帶
用於輸入與輸出,可以設想為一個無限長的紙帶,紙帶分為一個個單元格Rn,每個單元格上記錄某個字元表中的一個字元R(a),或者為空。
2讀寫頭
讀寫頭可以在紙帶上左右移動,其作用是:
讀取當前單元格里的字元;
擦除當前單元格里的字元;
將一個字元寫入當前單元格。
任意時刻讀寫頭只能在一個單元格上操作,此單元格稱為掃描單元格。
圖中的控制器可分解為下面的邏輯部件:
3字母表
字母表包括了輸入紙帶單元格上可以有的字元,讀寫頭可以寫入單元格的字元,比如字元集是{「1」「0」「+」「=」「︺」}。
4狀態集
圖靈機在任意時刻都處於一種狀態下,所有的狀態構成狀態集{s0、s1、s2、s3、s4、s5},其中包括:
開始狀態s0、每次執行的開始都處於此狀態;
停機狀態s5、當圖靈機進入此狀態時,機器就停止執行,此狀態下紙帶留下的字元為計算結果或者問題無解。
5控制規則
讀寫頭讀取當前單元格的字元,結合當前機器的狀態,可決定:
一、圖靈機的新狀態;
二、圖靈機的響應操作,包括:
擦除:擦除當前單元格的內容;
寫入:在當前單元格寫入字元集中的一個字元;
移動:向左移動或向右移動。
圖靈機的操作可抽象為:((當前狀態、當前讀入)→(新狀態、當前寫入、移動方向))。一個圖靈機可能的(當前狀態、當前讀入)組合稱為其格局,它們對應的控制規則決定了圖靈機的行為。我們構造個簡單的例子,這個例子是二進位制個位數的加法運算。設計七種狀態:(整體可以有不同的設計)
s0:初始狀態;
s1:被加數=1;
s2:被加數=0;
s3:被加數、加數=1;
s4:被加數、加數不一致;
s5:被加數、加數=0;
S6: 停機狀態。
字元表為{「1」「0」「+」}。
「擦除」操作表示清空單元格內容。
可制定的規則如下:
|
原狀態 |
讀取字元 |
寫入字元 |
移動方向 |
目標狀態 |
|
s0 |
1 |
1 |
右 |
S1 |
|
s0 |
0 |
擦除 |
右 |
S2 |
|
S1 |
+ |
+ |
右 |
S1 |
|
S2 |
+ |
+ |
右 |
S2 |
|
S1 |
1 |
擦除 |
左 |
S3 |
|
S1 |
0 |
擦除 |
左 |
S4 |
|
S2 |
1 |
1 |
左 |
S4 |
|
S2 |
0 |
擦除 |
左 |
S5 |
|
S3 |
+ |
0 |
無作用 |
S6 |
|
S4 |
+ |
擦除 |
無作用 |
S6 |
|
S5 |
+ |
擦除 |
無作用 |
S6 |
|
|
|
|
|
|
紙帶上的輸入是字串「1+0=」,將進行的過程如下:
|
過程 |
開始 |
結束 |
狀態 |
|
1 |
【1】+0 |
1+0 |
S0→s1 |
|
2 |
1【+】0 |
1+0 |
S1 |
|
3 |
1+【0】 |
1+ |
S1→s4 |
|
4 |
1【+】 |
1 |
S6 |
注:【】符號表示括號中的字母在當前單元格。
這是個過於簡單的例子。一般書上所能見到的例子都過於簡單,人們不禁會問:圖靈機能有什麼用?現代計算機所處理的問題越來越複雜,比如宇宙演化的模擬、天氣預報、自動駕駛等等,這些處理中也是應用同樣的機制,區別在於字元集、狀態集、規則集的數量級。
圖靈機的強大還在於可以構造通用圖靈機:可以模擬其他圖靈機的圖靈機。一臺解決特定問題的圖靈機,其字元表中的字元、狀態集的狀態、規則集中的規則,它們的數量都是有限的,因此它所有「((當前狀態、當前讀入)→(新狀態、當前寫入、移動方向))」可以以某種方式編碼,作為另一臺圖靈機紙帶上的特定輸入,同時它執行時的狀態、位置也在模擬時維護在通用圖靈機紙帶的特定單元格,這樣後一臺圖靈機通過讀取上的控制可以模擬前一臺圖靈機的執行。有了通用的圖靈機,我們就不必為每一類問題設計專門的圖靈機,只需要為通用的圖靈機設計不同的紙帶與控制就可以。目前已知最小的通用圖靈機是字元表的字元數量為2,狀態集的狀態數量為3的圖靈機,這比上面舉例還要簡單,理論上今天所有計算機的能力都不超過這臺最小的通用圖靈機,差別只在於效率上。
圖靈研究的直接背景是希爾伯特第十問題。1900年新世紀開始時,德國數學家希爾伯特在巴黎第二屆國際數學家大會上作了《數學問題》的著名講演,提出了數學理論中23個最困難的問題,後來這個世紀的數學進展與這23個問題的解決密切相關。其中的第10個問題也稱為判定性問題。原題目是:給定一個係數均為有理整數,包含任意多個未知數的丟番圖方程,能否設計一個過程,通過有限步驟的計算,判定出該方程在有理數上是否可解。問題的一般形式是:是否存在對任何可定義的數學問題可解的判定方法?圖靈研究論文的題目是「論數位計算在決斷難題中的應用」,他從數的可計算去研究可判定問題,數的可計算是個技術細節更單純的問題,同時圖靈證明了數的可計算問題與邏輯上可判定問題等價。
圖靈對於計算問題的研究是從觀察分析人用筆在紙上進行計算過程開始,他設想了一個裝置來模擬人的計算過程。圖靈機的讀寫頭相當於人的眼睛與手,紙帶的輸入是待求解的問題,狀態是對前面過程的一種記憶,根據輸入以及當前的狀態,匹配適用的規則產生新的狀態並進行寫入與移動操作,這與人用筆在紙上計算時的決策與操作過程類似。圖靈機裝置使所研究的問題具體化,一個數學問題的可計算等於此問題的圖靈機可計算。一個數學問題圖靈機可計算,此圖靈機就描述了此問題的演演算法。圖靈是回溯到如何施行計算操作以完成計算來研究可計算或可判定問題的,這其中包含的一個概念是演演算法,目前本書還沒有正式講到。以圖靈機的方式給出計算與演演算法的概念,在理論意義上,圖靈機可看作抽象的計算模型。從物理實現的方向考慮,圖靈機就是一種理論計算機的模型。由於技術上的原因,再發一篇文章後,最後的八篇只在同名公號裡釋出,本平臺存在未稽核通過的文章(即有斷號),也可到那裡閱讀。
回到原問題,希爾伯特的判定問題可歸為一臺通用圖靈機不通過實際模擬另一臺圖靈機,能否預測另一臺圖靈機的行為,如預測這臺圖靈機是否會停機。圖靈研究的結論是否定的,希爾伯特的判定問題無解。這是與哥德爾不完備定理同樣影響深遠的結論。圖靈機的思想及得到的結論,自圖靈以來一直刺激著更多的研究與討論,其中三個持續的主題是:
人的大腦是不是一臺圖靈機?
宇宙是不是一臺圖靈機?
在不違揹物理規律的情況下,能不能設計出超過通用圖靈機的機器?