Paddle Graph Learning (PGL)圖學習之圖遊走類模型[系列四]
Paddle Graph Learning (PGL)圖學習之圖遊走類模型[系列四]
更多詳情參考:Paddle Graph Learning 圖學習之圖遊走類模型[系列四]
https://aistudio.baidu.com/aistudio/projectdetail/5002782?contributionType=1
相關專案參考:
關於圖計算&圖學習的基礎知識概覽:前置知識點學習(PGL)[系列一] https://aistudio.baidu.com/aistudio/projectdetail/4982973?contributionType=1
圖機器學習(GML)&圖神經網路(GNN)原理和程式碼實現(前置學習系列二):https://aistudio.baidu.com/aistudio/projectdetail/4990947?contributionType=1
圖學習【參考資料1】詞向量word2vec https://aistudio.baidu.com/aistudio/projectdetail/5009409?contributionType=1
圖學習【參考資料2】-知識補充與node2vec程式碼註解 https://aistudio.baidu.com/aistudio/projectdetail/5012408?contributionType=1
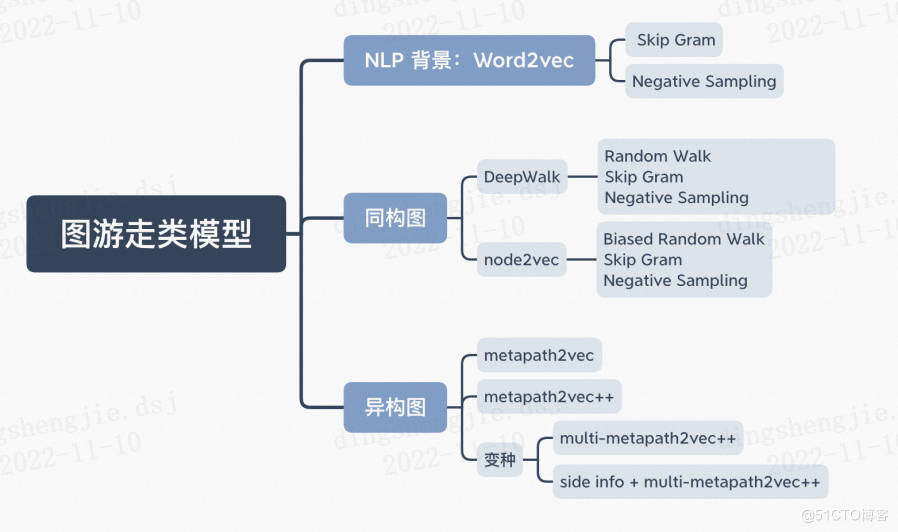
1.圖遊走類演演算法原理前言
1.1 Graph Embedding
在開始介紹圖遊走演演算法之前,先來學習一下什麼是Graph Embedding。
圖嵌入是一種將圖資料(通常為高維稠密的矩陣)對映為低微稠密向量的過程,如下圖所示。圖嵌入需要捕捉到圖的拓撲結構,頂點與頂點的關係,以及其他的資訊 (如子圖,連邊等)。如果有更多的資訊被表示出來,那麼下游的任務將會獲得更好的表現。在嵌入的過程中存在著一種共識:向量空間中保持連線的節點彼此靠近。

總的來說圖嵌入技術大致可以分為兩種:節點嵌入和圖嵌入。
- 當需要對節點進行分類,節點相似度預測,節點分佈視覺化時一般採用節點的嵌入;
- 當需要在圖級別(graph-level)上進行預測或者整個圖結構決策,需要將整個圖表示為一個向量進行嵌入表示。
圖學習的方法,大部分都可以應用到圖嵌入問題中,所以圖嵌入問題屬於圖學習中的一個非常重要的應用領域,不同的方法涉及了多方面知識。
我們可以將圖嵌入的這些方法簡要分為以下這些類別:
| 基於矩陣分解傳統方法 | 基於遊走策略 | 基於遊走策略和其他資訊 | 基於深度學習 | 基於GAN |
|---|---|---|---|---|
| Laplacian Eigenmaps | deepwalk | CENE | GCN | GraphGAN |
| Locally Linear Embedding | node2vec | CANE | SDNE | ANE |
| Graph Factorization | struc2vec | Trans-Net | ||
| LINE | ||||
| GraRep | ||||
| GraphSAGE |
1.1.1 為什麼要使用圖嵌入(graph embedding)
圖是一種簡單、易於理解的表示形式,但是由於下面的原因,我們需要對圖進行嵌入表示:
- 在graph上直接進行機器學習具有一定的侷限性,我們都知道圖是由節點和邊構成,這些向量關係一般只能使用數學,統計或者特定的子集進行表示,但是嵌入之後的向量空間具有更加靈活和豐富的計算方式。
- 圖嵌入能夠壓縮資料, 我們一般用鄰接矩陣描述圖中節點之間的連線。 連線矩陣的維度是$|V| \times|V|$,其中$|V|$ 是圖中節點的個數。矩陣中的每一列和每一行都代表一個節點。矩陣中的非零值表示兩個節點已連線。將鄰接矩陣用用大型圖的特徵空間幾乎是不可能的。一個具有1M節點和1M $\times$ 1M的鄰接矩陣的圖該怎麼表示和計算呢?但是嵌入可以看做是一種壓縮技術,能夠起到降維的作用。
- 向量計算比直接在圖上操作更加的簡單、快捷
但是圖嵌入也需要滿足一定的要求
- 學習屬性的選擇:不同的向量化表示方法,都是對網路資訊的一種摘要。有時我們會傾向於儲存網路中節點的近鄰關係,有時傾向學習節點在網路中的角色(比如中心節點)。不同的應用對「學習屬性」的選擇有不同的要求,故而引發了各類演演算法的爆發。
- 規模化:現實應用中有很多網路包含了大量的節點和邊,高效的向量化方法,能夠在短時間內處理超大規模的網路,才比較有實際應用的可能性。
- 向量維度:如何確定合適的向量表示維度,是一個很難的問題,並且也是和具體場景相關的。事實上,越高的維度可能帶來越好的效果,但是會極大降低應用效能。平衡效能和效果,在不同的應用中需要因地制宜。
1.2 詞語嵌入方法(word2vec)
node2vec是節點嵌入方法中的代表,而節點的嵌入方法借鑑了自然語言處理(NLP)中很一個重要的方法——word2vec。更多資料可以參考詞向量word2vec
該方法能夠成立的核心原因是:圖中的節點和語料庫中的單詞的分佈都遵循冪定律,我們可以利用基於大量資料的學習方法來找出節點之間、單詞之間的規律。

圖遊走演演算法:在圖上進行遊走得到遊走序列,通過圖表示學習利用節點之間的關係得到節點的一維表示,進而用這些一維表示進行下游人物。
圖遊走類演演算法的目標,就是學習出圖中每一個節點的低維表示,稱為 Node Embeddings,在得到這些 embeddings 之後,就可以利用這些低維表示來進行接下來的下游任務,比如節點分類之類的等等。
為什麼可以用這個低維表示來做下游任務呢?
因為可以利用一些方法,使得每個節點的 embeddings 可以學習到節點跟它的鄰居的關係,更好的表示圖結構和圖特徵的資訊。
圖遊走演演算法最先參考的是NLP的Word2vec模型,Word2vec模型的其中一種方法是Skip Gram,即根據中心詞預測上下文,之後通過負取樣的方式進行優化。
將Word2vec的思想和圖結合起來就會得到了圖遊走類演演算法
演演算法思想
假設,如果只給出蘋果這一個詞,而沒有其他的資訊,那麼,這個詞的詞義其實是模糊的。因為蘋果可能指的是水果,又或者是手機,但如果給出有關於蘋果的很多個句子:通過多個句子的上下文,其實可以大概瞭解到,上面所展示的蘋果這個詞的語意,是一種水果、一種食物。通過這個例子,可以得出這樣的一個結論,即詞的語意由其上下文決定。Word2vec 其實就是利用了這樣的一個思想。
整體架構
Word2vec 模型,可以簡單的理解為 Skip Gram + 負取樣

1.1.1 Skip Gram模型——根據中心詞預測上下文
在Word2vec 中,提出了兩種模型結構用於學習詞向量,分別是 CBOW 和 Skip Gram。由於圖遊走類演演算法用的多是 skip-gram 模型,因此這裡只介紹 skip-gram 模型。Skip Gram的目的很簡單,就是根據中心詞,預測對應中心詞的上下文詞。這樣做不僅僅能夠利用了詞共現關係,同時也體現了 Word2vec的本質,即詞的語意由其上下文來決定。
以下面這張圖片的句子為例,假設 neighbors 為中心詞,同時我們設定了window size為3. 這個視窗大小表示左右兩邊的上下文詞數,因此 neighbors 的 context 為 uniformly from the,以及 of the last。

Skip gram 的模型結構很簡單,輸入層就是中心詞的 one hot 表示,經過中間一個投影層後,在輸出層預測對應的context word,因此最後一層就是一個softmax分類層。
需要補充的一點是,使用 Skipgram語言模型的本質並不是為了說多麼準確的預測 context words,而是為了得到模型的副產物,也就是詞向量。
通常在訓練結束後,隱層的權重 W 會作為詞向量矩陣。
Word2Vec模型實際上分為了兩個部分:
- 第一部分為建立模型得到隱層引數,
- 第二部分是通過模型獲取嵌入詞向量。
Word2Vec的整個建模過程實際上與自編碼器(auto-encoder)的思想很相似,即先基於訓練資料構建一個神經網路,當這個模型訓練好以後,我們並不會用這個訓練好的模型處理新的任務,我們真正需要的是這個模型通過訓練資料所學得的引數,例如隱層的權重矩陣——後面我們將會看到這些權重在Word2Vec中實際上就是我們試圖去學習的「word vectors」。基於訓練資料建模的過程,我們給它一個名字叫「Fake Task」,意味著建模並不是我們最終的目的。
上面提到的這種方法實際上會在無監督特徵學習(unsupervised feature learning)中見到,最常見的就是自編碼器(auto-encoder):通過在隱層將輸入進行編碼壓縮,繼而在輸出層將資料解碼恢復初始狀態,訓練完成後,我們會將輸出層「砍掉」,僅保留隱層。
我們在上面提到,訓練模型的真正目的是獲得模型基於訓練資料學得的隱層權重。為了得到這些權重,我們首先要構建一個完整的神經網路作為我們的「Fake Task」,後面再返回來看通過「Fake Task」我們如何間接地得到這些詞向量。
模型的輸出概率代表著到我們詞典中每個詞有多大可能性跟input word同時出現。舉個栗子,如果我們向神經網路模型中輸入一個單詞「Soviet「,那麼最終模型的輸出概率中,像「Union」, 」Russia「這種相關詞的概率將遠高於像」watermelon「,」kangaroo「非相關詞的概率。因為」Union「,」Russia「在文字中更大可能在」Soviet「的視窗中出現。
我們將通過給神經網路輸入文字中成對的單詞來訓練它完成上面所說的概率計算。下面的圖中給出了一些我們的訓練樣本的例子。
我們選定句子「The quick brown fox jumps over lazy dog」,設定我們的視窗大小為2,也就是說我們僅選輸入詞前後各兩個詞和輸入詞進行組合。下圖中,藍色代表input word,方框內代表位於視窗內的單詞。

我們的模型將會從每對單詞出現的次數中習得統計結果。例如,我們的神經網路可能會得到更多類似(「fox」,「quick」)這樣的訓練樣本對,而相對而言,對於(「fox」,「lazy」)這樣的組合卻看到的很少。因此,當我們的模型完成訓練後,給定一個單詞「fox」作為輸入,輸出的結果中「quick」或者「jumps」要比「lazy」被賦予更高的概率。可以看到,我們總是以中間詞放在第一個位置,然後跟著我們的前後相鄰詞。可以看到,每一對詞都是一個輸入和一個輸出組成的資料對(X,Y)。其中,X是feature,Y是label。
我們都知道神經網路只能接受數值輸入,我們不可能把一個單詞字串作為輸入,因此我們得想個辦法來表示這些單詞。最常用的辦法就是基於訓練檔案來構建我們自己的詞彙表(vocabulary)再對單詞進行one-hot編碼。模型的輸入如果為一個10000維的向量,那麼輸出也是一個10000維度(詞彙表的大小)的向量,它包含了10000個概率,每一個概率代表著當前詞是輸入樣本中output word的概率大小。
我們把這樣的片語對分別表示成one-hot向量,input word的向量作為Fake Task網路的輸入,output word的向量作為學習的目標。

這樣,我們基於成對的單詞來對神經網路進行訓練,訓練樣本是 ( input word, output word ) 這樣的單詞對,input word和output word都是one-hot編碼的向量。最終模型的輸出是一個概率分佈。
如果我們現在想用300個特徵來表示一個單詞(即每個詞可以被表示為300維的向量)。那麼隱層的權重矩陣應該為10000行,300列(隱層有300個結點)。

Fake Task的訓練過程,我們最終的目標就是學習這個隱層的權重矩陣。
這個隱層的權重矩陣,便成了一個「查詢表(lookup table)」,進行矩陣計算時,直接去查輸入向量中取值為1的維度下對應的那些權重值。隱層的輸出就是每個輸入單詞的「嵌入詞向量」。
Word2Vec模型
經過神經網路隱層的計算,ants這個詞會從一個1 x 10000的向量變成1 x 300的向量,再被輸入到輸出層。輸出層是一個softmax迴歸分類器,它的每個結點將會輸出一個0-1之間的值(概率),這些所有輸出層神經元結點的概率之和為1。
現在,我們擁有10000個單詞的詞彙表,我們如果想嵌入300維的詞向量,那麼我們的輸入-隱層權重矩陣和隱層-輸出層的權重矩陣都會有 10000 x 300 = 300萬個權重,在如此龐大的神經網路中進行梯度下降是相當慢的。更糟糕的是,你需要大量的訓練資料來調整這些權重並且避免過擬合。百萬數量級的權重矩陣和億萬數量級的訓練樣本意味著訓練這個模型將會是個災難。
Word2Vec論文提出了三個創新點:
- 將常見的單詞組合(word pairs)或者片語作為單個「words」來處理。
- 對高頻次單詞抽樣來減少訓練樣本的個數。
- 對優化目標採用「negative sampling」方法,這樣每個訓練樣本的訓練只會更新一小部分的模型權重,從而降低計算負擔。
更多資料可以參考[詞向量word2vec]
1.1.2 Negative Sampling——負取樣
假設,給定中心詞 orange,預測其上下文詞中的 juice:

Softmax 層在 Skipgram 模型中是用來計算詞表的概率的。
為了能夠預測出 juice,不僅要預測它的概率,還要預測整個詞表中所有單詞的概率。但這樣做的計算量是非常大的,因此,這裡使用負取樣的方法進行優化。
負取樣的思想很簡單。將中心詞和對應的上下文詞作為正樣本,比如這裡的 (orange, juice)。同時,選取一定數量的負樣本,比如3個。
確定要正樣本和負樣本之後,就不再需要計算所有詞的概率,而只需要對這幾個樣本進行分類,如果 Y=1,意味著是正樣本,Y=0,意味著是負樣本。從而減少了計算量。
也就是把 softmax 層修改為了多個 sigmoid 函數,從而大大減少了計算量和參與權重更新的引數數目。
1.1.3 應用到圖嵌入領域

近朱者赤,近墨者黑。
也就是說,周遭的環境對於我們來說會有一定的影響,因此也可以表現為,圖中的節點會受到其鄰居的影響。
當然,這種情況也不僅僅只存在社群網路這個範圍內,在很多其他的圖,比如推薦系統等等,節點都會受到鄰居的影響。
這也是為什麼可以將Word2vec這個方法遷移到圖嵌入領域的原因
2.DeepWalk(原理+實踐)
遊走模型的鼻祖是DeepWalk模型,它也是第一個將 NLP 領域的思想運用到圖嵌入領域的模型。
2.1 節點嵌入方法(Node embeddings)
首先為什麼要用DeepWalk。我們可以觀察到,Word2Vec中,處理的是語句資料,詞語之間只有前後之間的聯絡,可以很自然的將句子中的詞語分成不同的片語。但是在圖資料中,節點與節點之前的聯絡——邊,邊的構成使得圖資料能夠比語句資料構成節點之間更加複雜的關係。通過遊走策略,我們可以將一個複雜的圖資料轉換為多個之後前後關聯的鏈路資料。

DeepWalk通過隨機遊走(truncated random walk)學習出一個網路的表示,在網路標註頂點很少的情況也能得到比較好的效果。隨機遊走起始於選定的節點,然後從當前節點移至隨機鄰居,並執行一定的步數,該方法大致可分為四個步驟:
- 圖a展示了原始的使用者行為序列。
- 圖b基於這些使用者行為序列構建了物品相關圖,可以看出,物品A,B之間的邊產生的原因就是因為使用者U1先後購買了物品A和物品B,所以產生了一條由A到B的有向邊。如果後續產生了多條相同的有向邊,則有向邊的權重被加強。在將所有使用者行為序列都轉換成物品相關圖中的邊之後,全域性的物品相關圖就建立起來了。
- 圖c採用隨機遊走的方式隨機選擇起始點,重新產生物品序列。
- 圖d最終將這些物品序列輸入word2vec模型,生成最終的物品Embedding向量。
在上述DeepWalk的演演算法流程中,核心是第三步,其中唯一需要形式化定義的是隨機遊走的跳轉概率,也就是到達節點$v_i$後,下一步遍歷$v_i$的臨接點$v_j$的概率。如果物品的相關圖是有向有權圖,那麼從節點$v_i$跳轉到節點$v_j$的概率定義如下:
$$P(v_{j}|v_{i})=\left{\begin{matrix}
\frac{M_{ij}}{\sum_{j\in N_+(v_{i})}M_{ij}} & , v_{j} \in N_+(v_{i}),\
0&, e_{ij}\notin \varepsilon
\end{matrix}\right.$$
其中$N_+(v_i)$是節點$v_i$所有的出邊集合,$M_{ij}$是節點$v_i$到節點$v_j$邊的權重。
如果物品相關圖是無相無權重圖,那麼跳轉概率將是上面公式的一個特例,即權重$M_{ij}$將為常數1,且$N_+(v_i)$應是節點$v_i$所有「邊」的集合,而不是所有「出邊」的集合。
DeepWalk通過隨機遊走去可以獲圖中點的區域性上下文資訊,因此學到的表示向量反映的是該點在圖中的區域性結構,兩個點在圖中共有的鄰近點(或者高階鄰近點)越多,則對應的兩個向量之間的距離就越短
整體架構
DeepWalk就相當於隨機遊走+Skip Gram+負取樣的結合

與 Word2vec 的不同,其實就是多了一個取樣節點序列的隨機遊走部分。因此這兩者實現起來其實是非常類似的。
在DeepWalk中,將每個節點看作是單詞,節點序列看作是句子。如下圖

Random Walk
不同於NLP中可以獲取很多的語料,DeepWalk採用了隨機遊走的方法來獲取節點序列(可回頭的深度優先搜尋)。下式中的π是節點的轉移概率分佈,Z是歸一化係數,在DeepWalk中可以理解成轉移到每一個鄰居節點的概率都是相同的。
具體過程

從圖中的某個節點出發,遊走的每一步都從與當前節點相連的邊中隨機選擇一條,沿著選定的邊移動到下一個頂點,不斷重複這個過程,直到得到的序列無法繼續往下走或者到達指定最大長度。
在走了多趟之後,便可以得到多個遊走序列,此時就可以類比 NLP 中的句子了。
隨機遊走的本質,其實就是可以「回頭」的深度優先搜尋
DeepWalk選取隨機遊走序列中下一個節點的方式是均勻隨機分佈的,因此對於與當前節點有邊相連的節點,都有相同的概率被選擇。
在 DeepWalk 中,會針對圖中的每個節點取樣多條序列,得到這些節點序列之後,就可以直接套用 Word2vec 模型了。
2.2 DeepWalk程式碼實現
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx # networkx是一個常用的繪製複雜圖形的Python包。
import pgl
def build_graph():
# 定義節點的個數;每個節點用一個數位表示,即從0~9
num_node = 10
# 新增節點之間的邊,每條邊用一個tuple表示為: (src, dst)
edge_list = [(2, 0), (2, 1), (3, 1),(4, 0), (0, 5),
(6, 0), (6, 4), (5, 6), (7, 0), (1, 7),
(2, 7), (7, 3), (8, 0), (9, 7)]
g = pgl.graph.Graph(num_nodes = num_node, edges = edge_list)
return g
# 建立一個圖物件,用於儲存圖網路的各種資料。
g = build_graph()
def display_graph(g):
nx_G = nx.Graph()
nx_G.add_nodes_from(range(g.num_nodes))
nx_G.add_edges_from(g.edges)
pos = nx.spring_layout(nx_G, iterations=50)
nx.draw(nx_G,
pos,
with_labels=True,
node_color=['y','g','g','g','y','y','y','g','y','g'],
node_size=1000)
plt.show()
display_graph(g)
def deepwalk(graph, start_node, walk_len):
walk = [start_node] # 初始化遊走序列
for d in range(walk_len): # 最大長度範圍內進行取樣
current_node = walk[-1]
successors = graph.successor(np.array([current_node])) # graph.successor: 獲取當前節點的後繼鄰居
print("當前節點: %d" % current_node)
print("後繼鄰居", successors[0])
succ = successors[0]
if len(succ) == 0:
break
next_node = np.random.choice(succ, 1)
walk.extend(next_node)
return walk
from pgl.graph import Graph
import numpy as np
class UserDefGraph(Graph):
def random_walk(self, nodes, walk_len):
"""
輸入:nodes - 當前節點id list (batch_size,)
walk_len - 最大路徑長度 int
輸出:以當前節點為起點得到的路徑 list (batch_size, walk_len)
用到的函數
1. self.successor(nodes)
描述:獲取當前節點的下一個相鄰節點id列表
輸入:nodes - list (batch_size,)
輸出:succ_nodes - list of list ((num_successors_i,) for i in range(batch_size))
2. self.outdegree(nodes)
描述:獲取當前節點的出度
輸入:nodes - list (batch_size,)
輸出:out_degrees - list (batch_size,)
"""
walks = [[node] for node in nodes] # 首先獲得當前節點列表對應的一個向量
walks_ids = np.arange(0, len(nodes)) # 遊走路徑中節點對應id號
cur_nodes = np.array(nodes) # 當前節點情況
for l in range(walk_len): # 根據遊走長度進行遍歷--破出條件:1. range結束;2. outdegree==0【出度為零,沒有可繼續的節點】
"""選取有下一個節點的路徑繼續取樣,否則結束"""
outdegree = self.outdegree(cur_nodes) # 計算當前節點的出度--也就是對應有哪些位置的鄰近節點
walk_mask = (outdegree != 0) # 根據出度來確定掩碼--True, False--將出度為0的部分複製為False,反之True
if not np.any(walk_mask): # 判斷是否沒有可繼續的節點情況--出度為0
break
cur_nodes = cur_nodes[walk_mask] # 根據掩碼獲取可繼續前進的節點,作為後邊討論的當前可前行節點
walks_ids = walks_ids[walk_mask] # 獲取掩碼下,原節點id,組成新的work_ids用於後邊討論,但本身還是作為一個節點的標記,對應這是第幾個節點
outdegree = outdegree[walk_mask] # 根據掩碼獲取相應的不為0的出度--用於後邊計算前行的路徑
######################################
# 請在此補充程式碼取樣出下一個節點
'''
[註解有點多,所以放外邊了]
PS:
1. successor 可獲取當前節點的下一個相鄰節點id列表,
那麼successor 計算出下一節點的集合後,我們需要從中隨機取出一個節點--所以我們要建立隨機取樣的index_list(索引序列集)
2. 建立index_list=>為了才到合適的index資訊,採用np.floor與np.random,rand()實現:
eg: np.floor(np.random.rand(outdegree.shape[0]) * outdegree).astype('int64')
np.random.rand(outdegree.shape[0]): 根據出度集的形狀來取得相應形狀的亂數--這裡體現遊走的隨機性
np.random.rand(outdegree.shape[0]) * outdegree:利用生成的亂數與出度集對應元素相乘——這裡得到一些列的亂數,亂數範圍在0~最大出度值--保證路徑有效
np.floor(np.random.rand(outdegree.shape[0]) * outdegree)——實現向下取整,這樣就得到了相應遊走路徑中接下來那個點的索引
具體範例:
np.floor(np.random.rand(20) * 3).astype('int64')
result: array([0, 1, 2, 1, 0, 0, 0, 0, 1, 1, 1, 2, 0, 2, 2, 2, 2, 1, 2, 0])
3. 既然知道了隨機取樣的序列集了,那麼接下就是分配新的遊走路徑了
next_nodes = [] # 用於後邊存放—— 裝配有下一個節點的新路徑
# 引數說明:
succ_nodes:相鄰節點id列表
sample_index:對應出度生成的隨即索引集
walks_ids:遊走路徑中節點對應id號
# 接下來的迴圈指的是,將節點列表、隨機取樣序列、遊走路徑中節點對應id號一一對應進行填充--得到一個遊走情況
for s, ind, walk_id in zip(succ_nodes, sample_index, walks_ids):
walks[walk_id].append(s[ind]) # 注意: 從開始已經知道walks=>[[], [], []]是這種形式的,這樣這裡的append,就很容易理解成為相應節點新增可以繼續前行的節點,形成一條路徑
next_nodes.append(s[ind]) # 同時獲取接下來要重新討論遊走時所需的新節點--即:如:從1走到了2,從3走到了7: [[1], [3]]=>[[1, 2], [3, 7]]
# 接下來自然就該考慮把新的2, 7 作為下一次遊走時討論出度的節點啦
'''
succ_nodes = self.successor(cur_nodes) # 返回可繼續的節點集合
# next_nodes = ...
sample_index = np.floor(np.random.rand(outdegree.shape[0]) * outdegree).astype('int64')
next_nodes = []
for s, ind, walk_id in zip(succ_nodes, sample_index, walks_ids):
walks[walk_id].append(s[ind])
next_nodes.append(s[ind])
######################################
cur_nodes = np.array(next_nodes) # 將節點轉換為np型別,方便一些操作運算--同時保證前後資料型別
# 遍歷完遊走長度的次數,就可以返回得到的隨機遊走路徑啦
return walks
因存在多版本問題(基於PGL1.2.1 paddle1.8),這部分的詳細實現參考連結:圖學習【參考資料2】-知識補充與node2vec程式碼註解 https://aistudio.baidu.com/aistudio/projectdetail/5012408?contributionType=1
結果展示:
[INFO] 2022-11-11 14:28:21,009 [my_deepwalk.py: 250]: Step 1170 DeepWalk Loss: 0.189346 0.239437 s/step.
[INFO] 2022-11-11 14:28:23,367 [my_deepwalk.py: 250]: Step 1180 DeepWalk Loss: 0.186947 0.230984 s/step.
[INFO] 2022-11-11 14:28:25,729 [my_deepwalk.py: 250]: Step 1190 DeepWalk Loss: 0.193626 0.233627 s/step.
[INFO] 2022-11-11 14:28:28,099 [my_deepwalk.py: 250]: Step 1200 DeepWalk Loss: 0.198106 0.242671 s/step.
[INFO] 2022-11-11 14:28:30,539 [my_deepwalk.py: 250]: Step 1210 DeepWalk Loss: 0.187183 0.309996 s/step.
[INFO] 2022-11-11 14:28:33,171 [my_deepwalk.py: 250]: Step 1220 DeepWalk Loss: 0.189533 0.244672 s/step.
[INFO] 2022-11-11 14:28:35,537 [my_deepwalk.py: 250]: Step 1230 DeepWalk Loss: 0.202293 0.232859 s/step.
[INFO] 2022-11-11 14:28:37,920 [my_deepwalk.py: 250]: Step 1240 DeepWalk Loss: 0.189366 0.244727 s/step.
[INFO] 2022-11-11 14:28:40,450 [my_deepwalk.py: 250]: Step 1250 DeepWalk Loss: 0.188601 0.254400 s/step.
[INFO] 2022-11-11 14:28:42,875 [my_deepwalk.py: 250]: Step 1260 DeepWalk Loss: 0.191343 0.247985 s/step.
[INFO] 2022-11-11 14:28:45,286 [my_deepwalk.py: 250]: Step 1270 DeepWalk Loss: 0.186549 0.255688 s/step.
[INFO] 2022-11-11 14:28:47,653 [my_deepwalk.py: 250]: Step 1280 DeepWalk Loss: 0.188638 0.240493 s/step.
[INFO] 2022-11-11 14:29:40,063 [link_predict.py: 223]: Step 160 Test Loss: 0.403480 Test AUC: 0.960065
[INFO] 2022-11-11 14:29:42,963 [link_predict.py: 199]: Step 170 Train Loss: 0.399953 Train AUC: 0.960795
[INFO] 2022-11-11 14:29:43,092 [link_predict.py: 223]: Step 170 Test Loss: 0.400902 Test AUC: 0.960164
[INFO] 2022-11-11 14:29:45,898 [link_predict.py: 199]: Step 180 Train Loss: 0.398023 Train AUC: 0.960870
[INFO] 2022-11-11 14:29:46,023 [link_predict.py: 223]: Step 180 Test Loss: 0.399052 Test AUC: 0.960234
[INFO] 2022-11-11 14:29:48,816 [link_predict.py: 199]: Step 190 Train Loss: 0.396805 Train AUC: 0.960916
[INFO] 2022-11-11 14:29:48,951 [link_predict.py: 223]: Step 190 Test Loss: 0.397910 Test AUC: 0.960275
[INFO] 2022-11-11 14:29:51,783 [link_predict.py: 199]: Step 200 Train Loss: 0.396290 Train AUC: 0.960936
[INFO] 2022-11-11 14:29:51,913 [link_predict.py: 223]: Step 200 Test Loss: 0.397469 Test AUC: 0.960292
3. node2vec(原理+實踐)
3.1 node2vec原理
Node2vec是圖表徵學習的一個重要的演演算法框架。
框架圖:

2016年,斯坦福大學在DeepWalk的基礎上更進一步,通過調整隨機遊走權重的方法使graph embedding的結果在網路的同質性(homophily)和結構性(structural equivalence)中進行權衡權衡。
具體來講,網路的「同質性」指的是距離相近節點的embedding應該儘量近似,如下圖所示,節點u與其相連的節點s1、s2、s3、s4的embedding表達應該是接近的,這就是「同質性「的體現。「結構性」指的是結構上相似的節點的embedding應該儘量接近,圖中節點u和節點s6都是各自區域網路的中心節點,結構上相似,其embedding的表達也應該近似,這是「結構性」的體現。
DeepWalk存在的問題是比較簡單直接,而圖結構往往是一個複雜結構,需要考慮很多因素,在深度優先搜尋方法之外,還有廣度優先搜尋,結合以上兩種方式可以更好的探索圖模型,即node2vec。

node2vec和DeepWalk相比主要修改的是轉移概率分佈,不同於隨機遊走相鄰節點轉移的概率相同,node2vec考慮了邊的權值和節點之間的距離,具體如下:
- 為了使Graph Embedding的結果能夠表達網路的同質性,在隨機遊走的過程中,需要讓遊走的過程更傾向於寬度優先搜尋(BFS),因為BFS更喜歡遊走到跟當前節點有直接連線的節點上,因此就會有更多同質性資訊包含到生成的樣本序列中,從而被embedding表達;
- 另一方面,為了抓住網路的結構性,就需要隨機遊走更傾向於深度優先搜尋(DFS),因為DFS會更傾向於通過多次跳轉,遊走到遠方的節點上,使得生成的樣本序列包含更多網路的整體結構資訊。
那麼在node2vec演演算法中,是怎樣控制BFS和DFS的傾向性的呢?主要是通過節點間的跳轉概率。下圖顯示了node2vec演演算法從節點t跳轉到節點v後,下一步從節點v跳轉到周圍各點的跳轉概率。

形式化來講,從節點v跳轉到下一個節點x的概率為
$$\pi _{VX}=\alpha _{pq}(t,x)\cdot \omega _{vx}$$
其中$\omega _{vx}$是邊vx的權重,$\alpha _{pq}(t,x)$的定義如下:
$$\alpha {pq}(t,x)=\left{\begin{matrix}
\frac{1}{p} & if \ d{tx}=0 & \
1 & if \ d_{tx}=1 & \
\frac{1} {q} & if \ d_{tx}=2 &
\end{matrix}\right.$$
其中,$d_{tx}$指的是節點$t$到節點$x$的距離,引數$p$和$q$共同控制著隨機遊走的傾向性。引數$p$被稱為返回引數(return parameter),$p$越小,隨機遊走回節點$t$的可能性越大,node2vec就更注重表達網路的同質性,引數$q$被稱為進出引數(in-out parameter),$q$越小,則隨機遊走到遠方節點的可能性越大,node2vec更注重表達網路的結構性,反之,當前節點更可能在附近節點遊走。
上式中的p和q是演演算法中的超引數,通過控制兩個引數來確定圖的遊走程度。引數p控制隨機遊走以多大的概率遊走回上一個節點,引數q控制遊走的策略是偏向DFS還是BFS,q較大時偏向於BFS,q較小時偏向於DFS。當p=q=1時,π=w
node2vec所體現的網路的同質性和結構性在推薦系統中也是可以被很直觀的解釋的。同質性相同的物品很可能是同品類、同屬性、或者經常被一同購買的物品,而結構性相同的物品則是各品類的爆款、各品類的最佳湊單商品等擁有類似趨勢或者結構性屬性的物品。毫無疑問,二者在推薦系統中都是非常重要的特徵表達。由於node2vec的這種靈活性,以及發掘不同特徵的能力,甚至可以把不同node2vec生成的embedding融合共同輸入後續深度學習網路,以保留物品的不同特徵資訊。
因存在多版本問題(基於PGL1.2.1 paddle1.8),這部分的詳細實現參考連結:圖學習【參考資料2】-知識補充與node2vec程式碼註解 https://aistudio.baidu.com/aistudio/projectdetail/5012408?contributionType=1
結果展示:
[INFO] 2022-11-11 14:37:32,694 [my_node2vec.py: 358]: Step 670 Node2vec Loss: 0.184862 0.288450 s/step.
[INFO] 2022-11-11 14:37:35,643 [my_node2vec.py: 358]: Step 680 Node2vec Loss: 0.180727 0.291284 s/step.
[INFO] 2022-11-11 14:37:39,554 [my_node2vec.py: 358]: Step 690 Node2vec Loss: 0.169635 0.441471 s/step.
[INFO] 2022-11-11 14:37:42,473 [my_node2vec.py: 358]: Step 700 Node2vec Loss: 0.172884 0.245686 s/step.
[INFO] 2022-11-11 14:37:45,268 [my_node2vec.py: 358]: Step 710 Node2vec Loss: 0.161657 0.261186 s/step.
[INFO] 2022-11-11 14:37:48,225 [my_node2vec.py: 358]: Step 720 Node2vec Loss: 0.167449 0.260464 s/step.
[INFO] 2022-11-11 14:37:51,188 [my_node2vec.py: 358]: Step 730 Node2vec Loss: 0.172065 0.297069 s/step.
[INFO] 2022-11-11 14:37:54,039 [my_node2vec.py: 358]: Step 740 Node2vec Loss: 0.168043 0.174017 s/step.
[INFO] 2022-11-11 14:38:49,260 [link_predict.py: 223]: Step 170 Test Loss: 0.454974 Test AUC: 0.954118
[INFO] 2022-11-11 14:38:51,997 [link_predict.py: 199]: Step 180 Train Loss: 0.452219 Train AUC: 0.955133
[INFO] 2022-11-11 14:38:52,122 [link_predict.py: 223]: Step 180 Test Loss: 0.453069 Test AUC: 0.954312
[INFO] 2022-11-11 14:38:54,851 [link_predict.py: 199]: Step 190 Train Loss: 0.450969 Train AUC: 0.955254
[INFO] 2022-11-11 14:38:54,978 [link_predict.py: 223]: Step 190 Test Loss: 0.451892 Test AUC: 0.954428
[INFO] 2022-11-11 14:38:57,714 [link_predict.py: 199]: Step 200 Train Loss: 0.450440 Train AUC: 0.955305
[INFO] 2022-11-11 14:38:57,842 [link_predict.py: 223]: Step 200 Test Loss: 0.451436 Test AUC: 0.954473
4.基於PGL2.2版本演演算法實現
4.1 資料集介紹
4.1.1 引文網路(Cora、PubMed、Citeseer)
引文網路,顧名思義就是由論文和他們的關係構成的網路,這些關係包括例如參照關係、共同的作者等,具有天然的圖結構,資料集的任務一般是論文的分類和連線的預測,比較流行的資料集有三個,分別是Cora、PubMed、Citeseer,它們的組成情況如圖1所示,Nodes也就是資料集的論文數量,features是每篇論文的特徵,資料集中有一個包含多個單詞的詞彙表,去除了出現頻率小於10的詞,但是不進行編碼,論文的屬性是由一串二進位制碼構成,只用0和1表示該論文有無這個詞彙。

檔案構成
- 以cora資料集為例,資料集包含兩個檔案,cora.cites和cora.content,cora.cites檔案中的資料如下:
- 即原論文和參照的論文,剛好構成了一條天然的邊,cora.content檔案的資料如下:
- 有論文id、上面說到的二進位制碼和論文對應的類別組成,其餘兩個資料集類似。
4.1.2 社群網路(BlogCatalog、Reddit、Epinions)
BlogCatalog資料集是一個社會關係網路,圖是由博主和他(她)的社會關係(比如好友)組成,labels是博主的興趣愛好。Reddit資料集是由來自Reddit論壇的貼文組成,如果兩個貼文被同一人評論,那麼在構圖的時候,就認為這兩個貼文是相關聯的,labels就是每個貼文對應的社群分類。Epinions是一個從一個線上商品評論網站收集的多圖資料集,裡面包含了多種關係,比如評論者對於另一個評論者的態度(信任/不信任),以及評論者對商品的評級。
檔案構成
BlogCatalog資料集的結點數為10312,邊條數為333983,label維度為39,資料集包含兩個檔案:
-
Nodes.csv:以字典的形式儲存使用者的資訊,但是隻包含節點id。
-
Edges.csv:儲存博主的社群網路(好友等),以此來構圖。
Epinions資料集包含檔案如下:
-
Ratings_data.txt:包含使用者對於一件物品的評級,檔案中每一行的結構為user_id
-
item_id rating_value。
-
Trust_data.txt:儲存了使用者對其他使用者的信任狀態,儲存方式為source_user_id
-
target_user_id trust_statement_value,其中信任狀態只有信任和不信任(1、0)。
由於Reddit comments 資料集的檔案太多,所以這裡略過了,如果需要或者感興趣的話,可以從文末的連線進入檢視。
相關論文:
Rossi, R. A. , & Ahmed, N. K. . (2015). The Network Data Repository with Interactive Graph Analytics and Visualization. Twenty-ninth Aaai Conference on Artificial Intelligence. AAAI Press.
4.1.3.生物化學結構(PPI、NCI-1、NCI-109、MUTAG、QM9、Tox21)
PPI是蛋白質互作網路,資料集中共有24張圖,其中20張作為訓練,2張作為驗證,2張作為測試,每張圖對應不同的人體組織,範例如圖3,該資料是為了從系統的角度研究疾病分子機制、發現新葯靶點等等。
平均每張圖有2372個結點,每個結點特徵長度為50,其中包含位置基因集,基序集和免疫學特徵。基因本體集作為labels(總共121個),labels不是one-hot編碼。
NCI-1、NCI-109和MUTAG是關於化學分子和化合物的資料集,原子代表結點,化學鍵代表邊。NCI-1和NCI-109資料集分別包含4100和4127個化合物,labels是判斷化合物是否有阻礙癌細胞增長得性質。MUTAG資料集包含188個硝基化合物,labels是判斷化合物是芳香族還是雜芳族。
QM9資料集包括了13萬有機分子的構成,空間資訊及其對應的屬性. 它被廣泛應用於各類資料驅動的分子屬性預測方法的實驗和對比。
Toxicology in the 21st Century 簡稱tox21,任務是使用化學結構資料預測化合物對生物化學途徑的干擾,研究、開發、評估和翻譯創新的測試方法,以更好地預測物質如何影響人類和環境。資料集有12707張圖,12個labels。
檔案構成
PPI資料集的構成:
train/test/valid_graph.json:儲存了訓練、驗證、測試的圖結構資料。
train/test/valid_feats.npy :儲存結點的特徵,以numpy.ndarry的形式儲存,shape為[n, v],n是結點的個數,v是特徵的長度。
train/test/valid_labels.npy:儲存結點的label,也是以numpy.ndarry的形式儲存,形為n*h,h為label的長度。
train/test/valid/_graph_id.npy :表示這個結點屬於哪張圖,形式為numpy.ndarry,例如[1, 1, 2, 1...20].。
NCI-1、NCI-109和MUTAG資料集的檔案構成如下:(用DS代替資料集名稱)
n表示結點數,m表示邊的個數,N表示圖的個數
DS_A.txt (m lines):圖的鄰接矩陣,每一行的結構為(row, col),即一條邊。
DS_graph_indicator.txt (n lines):表明結點屬於哪一個圖的檔案。
DS_graph_labels.txt (N lines):圖的labels。
DS_node_labels.txt (n lines):結點的labels。
DS_edge_labels.txt (m lines):邊labels。
DS_edge_attributes.txt (m lines):邊特徵。
DS_node_attributes.txt (n lines):結點的特徵。
DS_graph_attributes.txt (N lines):圖的特徵,可以理解為全域性變數。
QM9的檔案結構如下:
QM9_nano.npz:該檔案需要用numpy讀取,其中包含三個欄位:
'ID' 分子的id,如:qm9:000001;
'Atom' 分子的原子構成,為一個由原子序數的列表構成,如[6,1,1,1,1]表示該分子由一個碳(C)原子和4個氫(H)原子構成.;
'Distance' 分子中原子的距離矩陣,以上面[6,1,1,1,1]分子為例,它的距離矩陣即為一個5x5的矩陣,其中行列的順序和上述列表一致,即矩陣的第N行/列對應的是列表的第N個原子資訊.
'U0' 分子的能量屬性(溫度為0K時),也是我們需要預測的值(分類的種類為13)
Tox21資料夾中包含13個檔案,其中12個資料夾就是化合物的分類
4.1.4 ArXiv
http://snap.stanford.edu/data/ca-AstroPh.html
Arxiv ASTRO-PH(天體物理學)共同作業網路是來自電子版預影印平臺arXiv,涵蓋了提交到Astro Physics類別的論文,包含了不同作者之間的科學合作資訊。 如果作者i與作者j共同撰寫了論文,則該圖包含從i到j的無向邊。 如果論文由k位作者共同撰寫,則將在k個節點上生成完全連線的(子)圖。
資料涵蓋了1993年1月至2003年4月(124個月)期間的論文。 它始於arXiv成立後的幾個月內,因此基本上代表了其ASTRO-PH部分的完整歷史。
ArXiv資料集的結點數為18772,邊條數為198110。
相關論文
J. Leskovec, J. Kleinberg and C. Faloutsos. Graph Evolution: Densification and Shrinking Diameters. ACM Transactions on Knowledge Discovery from Data (ACM TKDD), 1(1), 2007.

4.1.5 下載地址
Cora:https://s3.us-east-2.amazonaws.com/dgl.ai/dataset/cora_raw.zip
Pubmed:https://s3.us-east-2.amazonaws.com/dgl.ai/dataset/pubmed.zip
Citeseer:https://s3.us-east-2.amazonaws.com/dgl.ai/dataset/citeseer.zip
BlogCatalog:http://socialcomputing.asu.edu/datasets/BlogCatalog
Reddit:https://github.com/linanqiu/reddit-dataset
Epinions:http://www.trustlet.org/downloaded_epinions.html
PPI:http://snap.stanford.edu/graphsage/ppi.zip
NCI-1:https://ls11-www.cs.uni-dortmund.de/people/morris/graphkerneldatasets/NCI1.zip
NCI-109:https://ls11-www.cs.uni-dortmund.de/people/morris/graphkerneldatasets/NCI109.zip
MUTAG:https://ls11-www.cs.uni-dortmund.de/people/morris/graphkerneldatasets/MUTAG.zip
QM9:https://github.com/geekinglcq/QM9nano4USTC
Tox21:https://tripod.nih.gov/tox21/challenge/data.jsp
4.2deepwalk(多類別預測任務)
資料集為:BlogCatalog
Paddle2.0+是動態圖了,為了進一步簡化使用,將GraphWrapper的概念去掉了,目前可以直接在Graph上進行Send/Recv
#uninstall pgl 2.1
python -m pip uninstall pgl
#install pgl 1.2.1
python -m pip install pgl==1.2.1
部分結果展示:
[INFO] 2022-11-13 22:44:29,956 [ train.py: 81]: Batch 7990 train-Loss 0.456979
[INFO] 2022-11-13 22:44:30,900 [ train.py: 81]: Batch 8000 train-Loss 0.457403
[INFO] 2022-11-13 22:44:31,791 [ train.py: 81]: Batch 8010 train-Loss 0.456784
[INFO] 2022-11-13 22:44:32,675 [ train.py: 81]: Batch 8020 train-Loss 0.453279
[INFO] 2022-11-13 22:44:33,593 [ train.py: 81]: Batch 8030 train-Loss 0.455351
[INFO] 2022-11-13 22:44:34,529 [ train.py: 81]: Batch 8040 train-Loss 0.455643
[INFO] 2022-11-13 22:44:35,388 [ train.py: 81]: Batch 8050 train-Loss 0.456534
100%|███████████████████████████████████████▊| 996/1000 [01:40<00:00, 9.86it/s][INFO] 2022-11-13 22:46:22,662 [multi_class.py: 150]: Train Loss: 0.095118 Train Macro F1: 0.440330 Train Micro F1: 0.473333
[INFO] 2022-11-13 22:46:22,710 [multi_class.py: 187]: Test Loss: 0.124781 Test Macro F1: 0.224703 Test Micro F1: 0.367081
100%|███████████████████████████████████████▉| 997/1000 [01:41<00:00, 9.88it/s][INFO] 2022-11-13 22:46:22,763 [multi_class.py: 150]: Train Loss: 0.095118 Train Macro F1: 0.440330 Train Micro F1: 0.473333
[INFO] 2022-11-13 22:46:22,812 [multi_class.py: 187]: Test Loss: 0.124784 Test Macro F1: 0.224703 Test Micro F1: 0.367081
100%|███████████████████████████████████████▉| 998/1000 [01:41<00:00, 9.88it/s][INFO] 2022-11-13 22:46:22,864 [multi_class.py: 150]: Train Loss: 0.095117 Train Macro F1: 0.440330 Train Micro F1: 0.473333
[INFO] 2022-11-13 22:46:22,913 [multi_class.py: 187]: Test Loss: 0.124788 Test Macro F1: 0.224703 Test Micro F1: 0.367081
100%|███████████████████████████████████████▉| 999/1000 [01:41<00:00, 9.89it/s][INFO] 2022-11-13 22:46:22,965 [multi_class.py: 150]: Train Loss: 0.095116 Train Macro F1: 0.440344 Train Micro F1: 0.473373
[INFO] 2022-11-13 22:46:23,013 [multi_class.py: 187]: Test Loss: 0.124791 Test Macro F1: 0.224703 Test Micro F1: 0.367081
100%|███████████████████████████████████████| 1000/1000 [01:41<00:00, 9.89it/s]
[INFO] 2022-11-13 22:46:23,014 [multi_class.py: 247]: Best test macro f1 is 0.2269956056437573.
4.3node2vec多類別預測任務)
部分結果展示:
[INFO] 2022-11-13 23:01:59,675 [ train.py: 81]: Batch 3950 train-Loss 0.569241
[INFO] 2022-11-13 23:02:01,468 [ train.py: 81]: Batch 3960 train-Loss 0.569519
[INFO] 2022-11-13 23:02:03,191 [ train.py: 81]: Batch 3970 train-Loss 0.569199
[INFO] 2022-11-13 23:02:04,906 [ train.py: 81]: Batch 3980 train-Loss 0.570791
[INFO] 2022-11-13 23:02:06,510 [ train.py: 81]: Batch 3990 train-Loss 0.569951
[INFO] 2022-11-13 23:02:08,249 [ train.py: 81]: Batch 4000 train-Loss 0.570624
[INFO] 2022-11-13 23:02:09,876 [ train.py: 81]: Batch 4010 train-Loss 0.567852
[INFO] 2022-11-13 23:02:11,495 [ train.py: 81]: Batch 4020 train-Loss 0.570603
100%|███████████████████████████████████████▉| 997/1000 [01:42<00:00, 9.85it/s][INFO] 2022-11-13 23:03:59,728 [multi_class.py: 150]: Train Loss: 0.096447 Train Macro F1: 0.352921 Train Micro F1: 0.471340
[INFO] 2022-11-13 23:03:59,777 [multi_class.py: 187]: Test Loss: 0.119648 Test Macro F1: 0.233598 Test Micro F1: 0.383243
100%|███████████████████████████████████████▉| 998/1000 [01:42<00:00, 9.83it/s][INFO] 2022-11-13 23:03:59,830 [multi_class.py: 150]: Train Loss: 0.096443 Train Macro F1: 0.352921 Train Micro F1: 0.471340
[INFO] 2022-11-13 23:03:59,879 [multi_class.py: 187]: Test Loss: 0.119651 Test Macro F1: 0.233497 Test Micro F1: 0.383210
100%|███████████████████████████████████████▉| 999/1000 [01:42<00:00, 9.83it/s][INFO] 2022-11-13 23:03:59,932 [multi_class.py: 150]: Train Loss: 0.096440 Train Macro F1: 0.352921 Train Micro F1: 0.471340
[INFO] 2022-11-13 23:03:59,980 [multi_class.py: 187]: Test Loss: 0.119654 Test Macro F1: 0.233497 Test Micro F1: 0.383210
100%|███████████████████████████████████████| 1000/1000 [01:42<00:00, 9.84it/s]
[INFO] 2022-11-13 23:03:59,981 [multi_class.py: 247]: Best test macro f1 is 0.2342214269132497.
4.4 結果對比
| Dataset | model | Task | Metric | PGL Result |
|---|---|---|---|---|
| BlogCatalog | deepwalk | multi-label classification | MacroF1 | 0.2269 |
| BlogCatalog | node2vec | multi-label classification | MacroF1 | 0.23422 |
這裡使用預設的引數,需要調優一下,0.260最佳效果。.
更多詳情參考:Paddle Graph Learning 圖學習之圖遊走類模型[系列四]
https://aistudio.baidu.com/aistudio/projectdetail/5002782?contributionType=1