圖學習【參考資料2】-知識補充與node2vec程式碼註解
本專案參考:
https://aistudio.baidu.com/aistudio/projectdetail/5012408?contributionType=1
*一、正題篇:DeepWalk、word2vec、node2vec
其它相關專案:
關於圖計算&圖學習的基礎知識概覽:前置知識點學習(PGL)[系列一] https://aistudio.baidu.com/aistudio/projectdetail/4982973?contributionType=1
圖機器學習(GML)&圖神經網路(GNN)原理和程式碼實現(前置學習系列二):https://aistudio.baidu.com/aistudio/projectdetail/4990947?contributionType=1
1.1 DeepWalk演演算法流程
【圖來源:網路,筆記由筆者添上】
演演算法流程:
【其中使用skip-gram模型是為了利用梯度的方法對引數進行更新訓練】
1.2 Skip Gram演演算法流程
【圖來源:網路,筆記由筆者添上】
演演算法流程: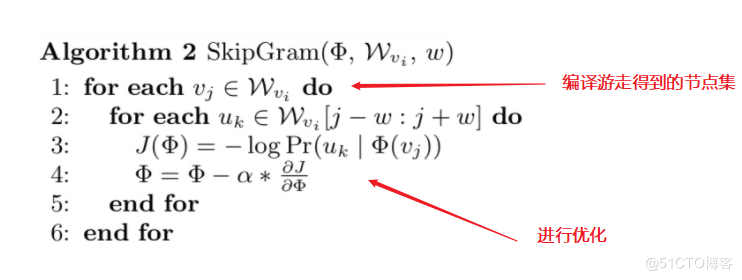
【其中使用skip-gram模型是為了利用梯度的方法對引數進行更新訓練】
此外,關於以上兩個演演算法的定義和概念就不一一展示說明了,後邊等有空了補上。下邊說一下我學習的一些參考資料,希望對大家有幫助。
參考資料
1.【論文筆記】DeepWalk——陌上疏影涼
1.【網路圖模型綜述
1.【異構圖神經網路簡介--機器之心
1.【Graph Embedding之metapath2vec--圈圈_Master
1.【從Random Walk談到Bacterial foraging optimization algorithm(BFOA),再談到Ramdom Walk Graph Segmentation圖分割演演算法
二 程式註解
【註解展示,是為了方便自己理解,同時也希望能幫到和自己一樣在學習這塊知識的小夥伴】
1.0 DeepWalk隨機遊走的實現

實現Graph類的random_walk函數--可參考
1.1 實現的參考程式碼--DeepWalk的隨機遊走演演算法實現
思路
- 理清successor,outdegree函數的輸入輸出
- 檢視補全函數的返回型別--分析可能的結果--我最初的猜測:這walks應該是多個向量的集合,最後確實也是【[[],..]這樣的結構多用於擴充,然後聯想需要學習向量,所以想到向量遞推的那種向量集合】
- 生成隨機取樣索引序列集 -- 這個需要匹配取樣形狀,以及索引閾值--我是參考一個範例修改的,感悟是: 利用亂數0~1,給rand傳入指定shape,再乘以一個相同shape的資料,可以得到一個>=0, <=最大出度-1的值,這樣就可以用來索引取樣了
- 理清上下文變數關係,進行zip打包遍歷到一起,然後進行聚合操作即可。
具體註解在程式碼中,可查閱,基本都是按照一行行註解的
from pgl.graph import Graph
import numpy as np
class UserDefGraph(Graph):
def random_walk(self, nodes, walk_len):
"""
輸入:nodes - 當前節點id list (batch_size,)
walk_len - 最大路徑長度 int
輸出:以當前節點為起點得到的路徑 list (batch_size, walk_len)
用到的函數
1. self.successor(nodes)
描述:獲取當前節點的下一個相鄰節點id列表
輸入:nodes - list (batch_size,)
輸出:succ_nodes - list of list ((num_successors_i,) for i in range(batch_size))
2. self.outdegree(nodes)
描述:獲取當前節點的出度
輸入:nodes - list (batch_size,)
輸出:out_degrees - list (batch_size,)
"""
walks = [[node] for node in nodes] # 首先獲得當前節點列表對應的一個向量
walks_ids = np.arange(0, len(nodes)) # 遊走路徑中節點對應id號
cur_nodes = np.array(nodes) # 當前節點情況
for l in range(walk_len): # 根據遊走長度進行遍歷--破出條件:1. range結束;2. outdegree==0【出度為零,沒有可繼續的節點】
"""選取有下一個節點的路徑繼續取樣,否則結束"""
outdegree = self.outdegree(cur_nodes) # 計算當前節點的出度--也就是對應有哪些位置的鄰近節點
walk_mask = (outdegree != 0) # 根據出度來確定掩碼--True, False--將出度為0的部分複製為False,反之True
if not np.any(walk_mask): # 判斷是否沒有可繼續的節點情況--出度為0
break
cur_nodes = cur_nodes[walk_mask] # 根據掩碼獲取可繼續前進的節點,作為後邊討論的當前可前行節點
walks_ids = walks_ids[walk_mask] # 獲取掩碼下,原節點id,組成新的work_ids用於後邊討論,但本身還是作為一個節點的標記,對應這是第幾個節點
outdegree = outdegree[walk_mask] # 根據掩碼獲取相應的不為0的出度--用於後邊計算前行的路徑
######################################
# 請在此補充程式碼取樣出下一個節點
'''
[註解有點多,所以放外邊了]
PS:
1. successor 可獲取當前節點的下一個相鄰節點id列表,
那麼successor 計算出下一節點的集合後,我們需要從中隨機取出一個節點--所以我們要建立隨機取樣的index_list(索引序列集)
2. 建立index_list=>為了才到合適的index資訊,採用np.floor與np.random,rand()實現:
eg: np.floor(np.random.rand(outdegree.shape[0]) * outdegree).astype('int64')
np.random.rand(outdegree.shape[0]): 根據出度集的形狀來取得相應形狀的亂數--這裡體現遊走的隨機性
np.random.rand(outdegree.shape[0]) * outdegree:利用生成的亂數與出度集對應元素相乘——這裡得到一些列的亂數,亂數範圍在0~最大出度值--保證路徑有效
np.floor(np.random.rand(outdegree.shape[0]) * outdegree)——實現向下取整,這樣就得到了相應遊走路徑中接下來那個點的索引
具體範例:
np.floor(np.random.rand(20) * 3).astype('int64')
result: array([0, 1, 2, 1, 0, 0, 0, 0, 1, 1, 1, 2, 0, 2, 2, 2, 2, 1, 2, 0])
3. 既然知道了隨機取樣的序列集了,那麼接下就是分配新的遊走路徑了
next_nodes = [] # 用於後邊存放—— 裝配有下一個節點的新路徑
# 引數說明:
succ_nodes:相鄰節點id列表
sample_index:對應出度生成的隨即索引集
walks_ids:遊走路徑中節點對應id號
# 接下來的迴圈指的是,將節點列表、隨機取樣序列、遊走路徑中節點對應id號一一對應進行填充--得到一個遊走情況
for s, ind, walk_id in zip(succ_nodes, sample_index, walks_ids):
walks[walk_id].append(s[ind]) # 注意: 從開始已經知道walks=>[[], [], []]是這種形式的,這樣這裡的append,就很容易理解成為相應節點新增可以繼續前行的節點,形成一條路徑
next_nodes.append(s[ind]) # 同時獲取接下來要重新討論遊走時所需的新節點--即:如:從1走到了2,從3走到了7: [[1], [3]]=>[[1, 2], [3, 7]]
# 接下來自然就該考慮把新的2, 7 作為下一次遊走時討論出度的節點啦
'''
succ_nodes = self.successor(cur_nodes) # 返回可繼續的節點集合
# next_nodes = ...
sample_index = np.floor(np.random.rand(outdegree.shape[0]) * outdegree).astype('int64')
next_nodes = []
for s, ind, walk_id in zip(succ_nodes, sample_index, walks_ids):
walks[walk_id].append(s[ind])
next_nodes.append(s[ind])
######################################
cur_nodes = np.array(next_nodes) # 將節點轉換為np型別,方便一些操作運算--同時保證前後資料型別
# 遍歷完遊走長度的次數,就可以返回得到的隨機遊走路徑啦
return walks
# 可增加輪次提高精度--epoch
# 當前引數精度大概在95%左右
!python my_deepwalk.py --use_my_random_walk --epoch 35 # 35 用自己實現的random walk訓練DeepWalk模型,可在 ./tmp/deepwalk/walks/ 中檢視構造的節點路徑
[INFO] 2022-11-11 14:28:28,099 [my_deepwalk.py: 250]: Step 1200 DeepWalk Loss: 0.198106 0.242671 s/step.
[INFO] 2022-11-11 14:28:30,539 [my_deepwalk.py: 250]: Step 1210 DeepWalk Loss: 0.187183 0.309996 s/step.
[INFO] 2022-11-11 14:28:33,171 [my_deepwalk.py: 250]: Step 1220 DeepWalk Loss: 0.189533 0.244672 s/step.
[INFO] 2022-11-11 14:28:35,537 [my_deepwalk.py: 250]: Step 1230 DeepWalk Loss: 0.202293 0.232859 s/step.
[INFO] 2022-11-11 14:28:37,920 [my_deepwalk.py: 250]: Step 1240 DeepWalk Loss: 0.189366 0.244727 s/step.
[INFO] 2022-11-11 14:28:40,450 [my_deepwalk.py: 250]: Step 1250 DeepWalk Loss: 0.188601 0.254400 s/step.
[INFO] 2022-11-11 14:28:42,875 [my_deepwalk.py: 250]: Step 1260 DeepWalk Loss: 0.191343 0.247985 s/step.
[INFO] 2022-11-11 14:28:45,286 [my_deepwalk.py: 250]: Step 1270 DeepWalk Loss: 0.186549 0.255688 s/step.
[INFO] 2022-11-11 14:28:47,653 [my_deepwalk.py: 250]: Step 1280 DeepWalk Loss: 0.188638 0.240493 s/step.
[INFO] 2022-11-11 14:29:45,898 [link_predict.py: 199]: Step 180 Train Loss: 0.398023 Train AUC: 0.960870
[INFO] 2022-11-11 14:29:46,023 [link_predict.py: 223]: Step 180 Test Loss: 0.399052 Test AUC: 0.960234
[INFO] 2022-11-11 14:29:48,816 [link_predict.py: 199]: Step 190 Train Loss: 0.396805 Train AUC: 0.960916
[INFO] 2022-11-11 14:29:48,951 [link_predict.py: 223]: Step 190 Test Loss: 0.397910 Test AUC: 0.960275
[INFO] 2022-11-11 14:29:51,783 [link_predict.py: 199]: Step 200 Train Loss: 0.396290 Train AUC: 0.960936
[INFO] 2022-11-11 14:29:51,913 [link_predict.py: 223]: Step 200 Test Loss: 0.397469 Test AUC: 0.960292
2.0 SkipGram模型訓練
NOTE:在得到節點路徑後,node2vec會使用SkipGram模型學習節點表示,給定中心節點,預測區域性路徑中還有哪些節點。模型中用了negative sampling來降低計算量。

參考 PGL/examples/node2vec/node2vec.py 中的 node2vec_model 函數
2.1 SkipGram模型實現程式碼參考--理解
- 這部分的話,官方程式碼已經給的很清晰了,這裡主要是做一些解釋補充--大都可以跟上邊演演算法公式對應著看
- 這裡採用組合損失--組合損失計算時,要注意在不必要的引數建立後,記得關閉梯度記錄--否則會對他求梯度,這樣不太好:
如:ones_label,他只是一箇中間量,用於存放結果的,不需要對他求梯度,因為不需要優化它 - 還有一點,靜態圖下,儘量使用layers下的運算方法,避免出現超出計算圖的一些邏輯迴圈操作
這一部分沒什麼好說的,大家理解就好--多看看原始碼哦!
import paddle.fluid.layers as l
def userdef_loss(embed_src, weight_pos, weight_negs):
"""
輸入:embed_src - 中心節點向量 list (batch_size, 1, embed_size)
weight_pos - 標籤節點向量 list (batch_size, 1, embed_size)
weight_negs - 負樣本節點向量 list (batch_size, neg_num, embed_size)
輸出:loss - 正負樣本的交叉熵 float
"""
##################################
# 請在這裡實現SkipGram的loss計算過程
### 負取樣計算部分——Multi Sigmoids
# 分別計算正樣本和負樣本的 logits(概率)
pos_logits = l.matmul(
embed_src, weight_pos, transpose_y=True) # [batch_size, 1, 1] -- matmul:矩陣相乘
neg_logits = l.matmul(
embed_src, weight_negs, transpose_y=True) # [batch_size, 1, neg_num]
# 設定正樣本標籤,並計算正樣本loss
ones_label = pos_logits * 0. + 1.
ones_label.stop_gradient = True # 關閉梯度記錄
pos_loss = l.sigmoid_cross_entropy_with_logits(pos_logits, ones_label) # 交叉熵計算==對應公式2
# 設定負樣本標籤,並計算負樣本loss
zeros_label = neg_logits * 0.
zeros_label.stop_gradient = True
neg_loss = l.sigmoid_cross_entropy_with_logits(neg_logits, zeros_label) # 交叉熵計算==對應公式3
# 總的Loss計算為正樣本與負樣本loss之和
loss = (l.reduce_mean(pos_loss) + l.reduce_mean(neg_loss)) / 2 # 得到總的loss
##################################
return loss
NOTE:Node2Vec會根據與上個節點的距離按不同概率取樣得到當前節點的下一個節點。
<img src="https://ai-studio-static-online.cdn.bcebos.com/09001163a1064101a8dd2892eb559cf2006aa93d7fe84c70b2ad47b810f4c86a" width="85%" height="85%" /><br>
參考; PGL/pgl/graph_kernel.pyx 中用Cython語言實現了節點取樣函數node2vec_sample
3.1 Node2Vec取樣演演算法轉換程式碼註解
- 這部分程式碼,用於隨機遊走後得到的路徑,然後對這些路徑進行吸收學習,訓練圖結構
import numpy as np
# 隨機節點的獲取
def node2vec_sample(succ, prev_succ, prev_node, p, q):
"""
輸入:succ - 當前節點的下一個相鄰節點id列表 list (num_neighbors,)
prev_succ - 前一個節點的下一個相鄰節點id列表 list (num_neighbors,)
prev_node - 前一個節點id int
p - 控制回到上一節點的概率 float
q - 控制偏向DFS還是BFS float
輸出:下一個節點id int
"""
##################################
# 請在此實現node2vec的節點取樣函數
# 節點引數資訊
succ_len = len(succ) # 獲取相鄰節點id列表節點長度(相對當前)
prev_succ_len = len(prev_succ) # 獲取相鄰節點id列表節點長度(相對前一個節點)
prev_succ_set = np.asarray([]) # 前一節點的相鄰節點id列表
for i in range(prev_succ_len): # 遍歷得到前一節點的相鄰節點id列表的新list——prev_succ_set,用於後邊概率的討論
# 將前一節點list,依次押入新的list中
prev_succ_set = np.append(prev_succ_set,prev_succ[i]) # ? prev_succ_set.insert(prev_succ[i])
# 概率引數資訊
probs = [] # 儲存每一個待前往的概率
prob = 0 # 記錄當前討論的節點概率
prob_sum = 0. # 所有待前往的節點的概率之和
# 遍歷當前節點的相鄰節點
for i in range(succ_len): # 遍歷每一個當前節點前往的概率
if succ[i] == prev_node: # case 1 : 取樣節點與前一節點一致,那麼概率為--1/q(原地)
prob = 1. / p
# case 2 完整的應該是: np.where(prev_succ_set==succ[i]) and np.where(succ==succ[i])
# 但是因為succ本身就是取樣集,所以np.where(succ==succ[i])總成立,故而忽略,不考慮
elif np.where(prev_succ_set==succ[i]): # case 2 : 取樣節點在前一節點list內,那麼概率為--1 ?cpython中的程式碼: prev_succ_set.find(succ[i]) != prev_succ_set.end()
prob = 1.
elif np.where(prev_succ_set!=succ[i]): # case 3 : 取樣節點不在前一節點list內,那麼概率為--1/q
prob = 1. / q
else:
prob = 0. # case 4 : other
probs.append(prob) # 將待前往的每一個節點的概率押入儲存
prob_sum += prob # 計算所有節點的概率之和
RAND_MAX = 65535 # 這是一個亂數的最值,用於計算隨機值的--根據C/C++標準,最小在30000+,這裡取2^16次方
rand_num = float(np.random.randint(0, RAND_MAX+1)) / RAND_MAX * prob_sum # 計算一個隨機概率:0~prob_sum. ?cpython中的程式碼: float(rand())/RAND_MAX * prob_sum
sampled_succ = 0. # 當前節點的相鄰節點中確定的取樣點
# rand_num => 是0~prob_num的一個值,表示我們的擷取概率閾值--即當遍歷了n個節點時,若已遍歷的節點的概率之和已經超過了rand_num
# 我們取剛好滿足已遍歷的節點的概率之和已經超過了rand_num的最近一個節點作為我們的取樣節點
# 比如: 遍歷到第5個節點時,權重概率和大於等於rand_num,此時第5個節點就是對應的取樣的節點了
# 為了方便實現:這裡利用迴圈遞減--判斷條件就變成了————當rand_num減到<=0時,開始取樣節點
for i in range(succ_len): # 遍歷當前節點的所有相鄰節點
rand_num -= probs[i] # 利用rand_num這個隨機獲得的概率值作為依據,進行一個迴圈概率檢驗
if rand_num <= 0: # 當遇到第一次使得rand_num減到<=0後,說明到這個節點為止, 遍歷應該終止了,此時的節點即未所求的節點,【停止檢驗條件】
sampled_succ = succ[i] # 並把當前節點作為確定的節點
return sampled_succ # 返回待取樣的節點--節點一定在succ中
[INFO] 2022-11-11 14:38:49,133 [link_predict.py: 199]: Step 170 Train Loss: 0.454199 Train AUC: 0.954936
[INFO] 2022-11-11 14:38:49,260 [link_predict.py: 223]: Step 170 Test Loss: 0.454974 Test AUC: 0.954118
[INFO] 2022-11-11 14:38:51,997 [link_predict.py: 199]: Step 180 Train Loss: 0.452219 Train AUC: 0.955133
[INFO] 2022-11-11 14:38:52,122 [link_predict.py: 223]: Step 180 Test Loss: 0.453069 Test AUC: 0.954312
[INFO] 2022-11-11 14:38:54,851 [link_predict.py: 199]: Step 190 Train Loss: 0.450969 Train AUC: 0.955254
[INFO] 2022-11-11 14:38:54,978 [link_predict.py: 223]: Step 190 Test Loss: 0.451892 Test AUC: 0.954428
[INFO] 2022-11-11 14:38:57,714 [link_predict.py: 199]: Step 200 Train Loss: 0.450440 Train AUC: 0.955305
[INFO] 2022-11-11 14:38:57,842 [link_predict.py: 223]: Step 200 Test Loss: 0.451436 Test AUC: 0.954473
1. 回顧並總結了圖的基本概念。<br>
2. 學習思考演演算法實現的程式碼思路--Node2Vec的實現以及RandomWalk的實現。<br>
3. 對原始碼閱讀能力的提升。<br>
其它相關筆記:<br>
關於圖計算&圖學習的基礎知識概覽:前置知識點學習(PGL)[系列一] https://aistudio.baidu.com/aistudio/projectdetail/4982973?contributionType=1
圖機器學習(GML)&圖神經網路(GNN)原理和程式碼實現(前置學習系列二):https://aistudio.baidu.com/aistudio/projectdetail/4990947?contributionType=1
<br>
* 如果我的專案對你有幫助不如點一個心,fork一下,以備可以常複習哦!