圖機器學習(GML)&圖神經網路(GNN)原理和程式碼實現(前置學習系列二)
專案連結:https://aistudio.baidu.com/aistudio/projectdetail/4990947?contributionType=1
歡迎fork歡迎三連!文章篇幅有限,部分程式出圖不一一展示,詳情進入專案連結即可
圖機器學習(GML)&圖神經網路(GNN)原理和程式碼實現(PGL)[前置學習系列二]
上一個專案對圖相關基礎知識進行了詳細講述,下面進圖GML
networkx :NetworkX 是一個 Python 包,用於建立、操作和研究複雜網路的結構、動力學和功能
https://networkx.org/documentation/stable/reference/algorithms/index.html
import numpy as np
import random
import networkx as nx
from IPython.display import Image
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
1. 圖機器學習GML
圖學習的主要任務
圖學習中包含三種主要的任務:
- 連結預測(Link prediction)
- 節點標記預測(Node labeling)
- 圖嵌入(Graph Embedding)
1.1連結預測(Link prediction)
在連結預測中,給定圖G,我們的目標是預測新邊。例如,當圖未被完全觀察時,或者當新客戶加入平臺(例如,新的LinkedIn使用者)時,預測未來關係或缺失邊是很有用的。
詳細闡述一下就是:
GNN連結預測任務,即預測圖中兩個節點之間的邊是否存在。在Social Recommendation,Knowledge Graph Completion等應用中都需要進行連結預測。模型實現上是將連結預測任務看成一個二分類任務:
- 將圖中存在的邊作為正樣本;
- 負取樣一些圖中不存在的邊作為負樣本;
- 將正樣例和負樣例合併劃分為訓練集和測試集;
- 可以採用二分類模型的評估指標來評估模型的效果,
例如:AUC值在一些場景下例如大規模推薦系統或資訊檢索,模型需要評估top-k預測結果的準確性,因此對於連結預測任務還需要一些其他的評估指標來衡量模型最終效果:
- MR(MeanRank)
- MRR(Mean Reciprocal Rank)
- Hit@n
MR, MRR, Hit@n指標含義:假設整個圖譜中共n個實體,評估前先進行如下操作:
(1)將一個正確的三元組(h,r,t)中的頭實體h或者尾實體t,依次替換成整個圖譜中的其他所有實體,這樣會產生n個三元組;
(2)對(1)中產生的n個三元組分別計算其能量值,例如在TransE中計算h+r-t的值,這樣n個三元組分別對應自己的能量值;
(3)對上述n個三元組按照能量值進行升序排序,記錄每個三元組排序後的序號;
(4)對所有正確的三元組都進行上述三步操作MR指標:將整個圖譜中每個正確三元組的能量值排序後的序號取平均得到的值;
- MRR指標:將整個圖譜每個正確三元組的能量排序後的序號倒數取平均得到的值;
- Hit@n指標:整個圖譜正確三元組的能量排序後序號小於n的三元組所佔的比例。因此對於連結預測任務來說,MR指標越小,模型效果越好;
- MRR和Hit@n指標越大,模型效果越好。接下來本文將在Cora引文資料集上,預測兩篇論文之間是否存在參照關係或被參照關係
新LinkedIn使用者的連結預測只是給出它可能認識的人的建議。
在鏈路預測中,我們只是嘗試在節點對之間建立相似性度量,並連結最相似的節點。現在的問題是識別和計算正確的相似性分數!
為了說明圖中不同鏈路的相似性差異,讓我們通過下面這個圖來解釋:
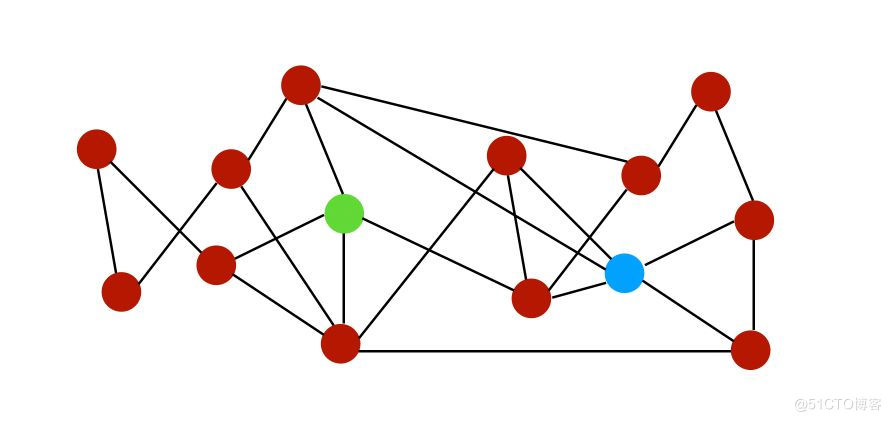
設$N(i)$是節點$i$的一組鄰居。在上圖中,節點$i$和$j$的鄰居可以表示為:

$i$的鄰居:

1.1.1 相似度分數
我們可以根據它們的鄰居為這兩個節點建立幾個相似度分數。
- 公共鄰居:$S(i,j) = \mid N(i) \cap N(j) \mid$,即公共鄰居的數量。在此範例中,分數將為2,因為它們僅共用2個公共鄰居。

- Jaccard係數:$S(i,j) = \frac { \mid N(i) \cap N(j) \mid } { \mid N(i) \cup N(j) \mid }$,標準化的共同鄰居版本。
交集是共同的鄰居,並集是:

因此,Jaccard係數由粉紅色與黃色的比率計算出:

值是$\frac {1} {6}$。
- Adamic-Adar指數:$S(i,j) = \sum_{k \in N(i)\cap N(j) } \frac {1} {\log \mid N(k) \mid}$。 對於節點i和j的每個公共鄰居(common neighbor),我們將1除以該節點的鄰居總數。這個概念是,當預測兩個節點之間的連線時,與少量節點之間共用的元素相比,具有非常大的鄰域的公共元素不太重要。
- 優先依附(Preferential attachment): $S(i,j) = \mid N(i) \mid * \mid N(j) \mid$
- 當社群資訊可用時,我們也可以在社群資訊中使用它們。
1.1.2 效能指標(Performance metrics)
我們如何進行連結預測的評估?我們必須隱藏節點對的子集,並根據上面定義的規則預測它們的連結。這相當於監督學習中的train/test的劃分。
然後,我們評估密集圖的正確預測的比例,或者使用稀疏圖的標準曲線下的面積(AUC)。
參考連結:模型評估指標AUC和ROC:https://cloud.tencent.com/developer/article/1508882
1.1.3 程式碼實踐
這裡繼續用空手道俱樂部圖來舉例:
使用在前兩篇文中提及到的Karate圖,並使用python來進行實現
n=34
m = 78
G_karate = nx.karate_club_graph()
pos = nx.spring_layout(G_karate)
nx.draw(G_karate, cmap = plt.get_cmap('rainbow'), with_labels=True, pos=pos)
# 我們首先把有關圖的資訊列印出來:
n = G_karate.number_of_nodes()
m = G_karate.number_of_edges()
print("Number of nodes : %d" % n)
print("Number of edges : %d" % m)
print("Number of connected components : %d" % nx.number_connected_components(G_karate))
plt.figure(figsize=(12,8))
nx.draw(G_karate, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")
# 現在,讓刪除一些連線,例如25%的邊:
# Take a random sample of edges
edge_subset = random.sample(G_karate.edges(), int(0.25 * G_karate.number_of_edges()))
# remove some edges
G_karate_train = G_karate.copy()
G_karate_train.remove_edges_from(edge_subset)
# 繪製部分觀察到的圖,可以對比上圖發現,去掉了一些邊
plt.figure(figsize=(12,8))
nx.draw(G_karate_train, pos=pos)
# 可以列印我們刪除的邊數和剩餘邊數:
edge_subset_size = len(list(edge_subset))
print("Deleted : ", str(edge_subset_size))
print("Remaining : ", str((m - edge_subset_size)))
# Jaccard Coefficient
# 可以先使用Jaccard係數進行預測:
pred_jaccard = list(nx.jaccard_coefficient(G_karate_train))
score_jaccard, label_jaccard = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_jaccard])
# 列印前10組結果
print(pred_jaccard[0:10])
# 預測結果如下,其中第一個是節點,第二個是節點,最後一個是Jaccard分數(用來表示兩個節點之間邊預測的概率)
# Compute the ROC AUC Score
# 其中,FPR是False Positive Rate, TPR是True Positive Rate
fpr_jaccard, tpr_jaccard, _ = roc_curve(label_jaccard, score_jaccard)
auc_jaccard = roc_auc_score(label_jaccard, score_jaccard)
print(auc_jaccard)
# Adamic-Adar
# 現在計算Adamic-Adar指數和對應的ROC-AUC分數
# Prediction using Adamic Adar
pred_adamic = list(nx.adamic_adar_index(G_karate_train))
score_adamic, label_adamic = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_adamic])
print(pred_adamic[0:10])
# Compute the ROC AUC Score
fpr_adamic, tpr_adamic, _ = roc_curve(label_adamic, score_adamic)
auc_adamic = roc_auc_score(label_adamic, score_adamic)
print(auc_adamic)
# Compute the Preferential Attachment
# 同樣,可以計算Preferential Attachment得分和對應的ROC-AUC分數
pred_pref = list(nx.preferential_attachment(G_karate_train))
score_pref, label_pref = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_pref])
print(pred_pref[0:10])
fpr_pref, tpr_pref, _ = roc_curve(label_pref, score_pref)
auc_pref = roc_auc_score(label_pref, score_pref)
print(auc_pref)
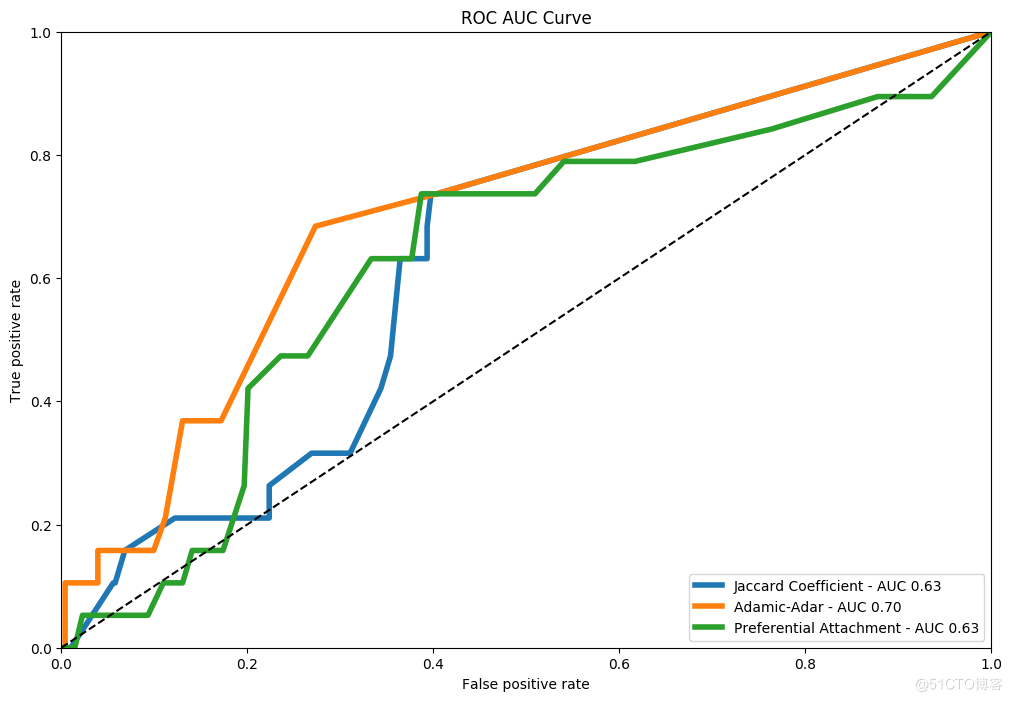
plt.figure(figsize=(12, 8))
plt.plot(fpr_jaccard, tpr_jaccard, label='Jaccard Coefficient - AUC %.2f' % auc_jaccard, linewidth=4)
plt.plot(fpr_adamic, tpr_adamic, label='Adamic-Adar - AUC %.2f' % auc_adamic, linewidth=4)
plt.plot(fpr_pref, tpr_pref, label='Preferential Attachment - AUC %.2f' % auc_pref, linewidth=4)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title("ROC AUC Curve")
plt.legend(loc='lower right')
plt.show()
1.2 節點標記預測(Node labeling)
給定一個未標記某些節點的圖,我們希望對這些節點的標籤進行預測。這在某種意義上是一種半監督的學習問題。
處理這些問題的一種常見方法是假設圖上有一定的平滑度。平滑度假設指出通過資料上的高密度區域的路徑連線的點可能具有相似的標籤。這是標籤傳播演演算法背後的主要假設。
標籤傳播演演算法(Label Propagation Algorithm,LPA)是一種快速演演算法,僅使用網路結構作為指導來發現圖中的社群,而無需任何預定義的目標函數或關於社群的先驗資訊。

單個標籤在密集連線的節點組中迅速佔據主導地位,但是在穿過稀疏連線區域時會遇到問題。
半監督標籤傳播演演算法是如何工作?
首先,我們有一些資料:$x_1, ..., x_l, x_{l+1}, ..., x_n \in R^p$,,以及前$l$個點的標籤:$y_1, ..., y_l \in 1...C$.
我們定義初始標籤矩陣$Y \in R^{n \times C}$,如果$x_i$具有標籤$y_i=j$則$Y_{ij} = 1$,否則為0。
該演演算法將生成預測矩陣$F \in R^{n \times C}$,我們將在下面詳述。然後,我們通過查詢最可能的標籤來預測節點的標籤:
$\hat{Y_i} = argmax_j F_{i,j}$
預測矩陣$F$是什麼?
預測矩陣是矩陣$F^{\star}$,其最小化平滑度和準確度。因此,我們的結果在平滑性和準確性之間進行權衡。
問題的描述非常複雜,所以我將不會詳細介紹。但是,解決方案是:
$F^{\star} = ( (1-\alpha)I + L_{sym})^{-1} Y$
其中:
- 引數$\alpha = \frac {1} {1+\mu}$
- $Y$是給定的標籤
- $L_{sym}$是圖的歸一化拉普拉斯矩陣(Laplacian matrix)
如果您想進一步瞭解這個主題,請關注圖函數的平滑度和流形正則化的概念。斯坦福有一套很好的標籤圖可以下載:https://snap.stanford.edu/data/
接下來我們用python來實現節點標籤的預測。
為了給我們使用到的標籤新增更多的特徵,我們需要使用來自Facebook的真實資料。你可以再這裡下載,然後放到facebook路徑下。

Facebook 資料已通過將每個使用者的 Facebook 內部 id 替換為新值來匿名化。此外,雖然已經提供了來自該資料集的特徵向量,但對這些特徵的解釋卻很模糊。例如,如果原始資料集可能包含特徵「political=Democratic Party」,則新資料將僅包含「political=anonymized feature 1」。因此,使用匿名資料可以確定兩個使用者是否具有相同的政治派別,但不能確定他們各自的政治派別代表什麼。
我已經把資料集放在目錄裡了,就不需要下載了
1.2.1 程式碼實現標籤擴散
n = G_fb.number_of_nodes()
m = G_fb.number_of_edges()
print("Number of nodes: %d" % n)
print("Number of edges: %d" % m)
print("Number of connected components: %d" % nx.number_connected_components(G_fb))
# 我們把圖資料顯示出來:
mapping=dict(zip(G_fb.nodes(), range(n)))
nx.relabel_nodes(G_fb, mapping, copy=False)
pos = nx.spring_layout(G_fb)
plt.figure(figsize=(12,8))
nx.draw(G_fb, node_size=200, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")
with open('facebook/3980.featnames') as f:
for i, l in enumerate(f):
pass
n_feat = i+1
features = np.zeros((n, n_feat))
f = open('facebook/3980.feat', 'r')
for line in f:
if line.split()[0] in mapping:
node_id = mapping[line.split()[0]]
features[node_id, :] = list(map(int, line.split()[1:]))
features = 2*features-1
feat_id = 6 #特徵選擇id,自行設定
labels = features[:, feat_id]
plt.figure(figsize=(12,8))
nx.draw(G_fb, cmap = plt.get_cmap('bwr'), nodelist=range(n), node_color = labels, node_size=200, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")
plt.show()
# 這個所選擇的特徵,在圖中相對平滑,因此擁有較好的學習傳播效能。
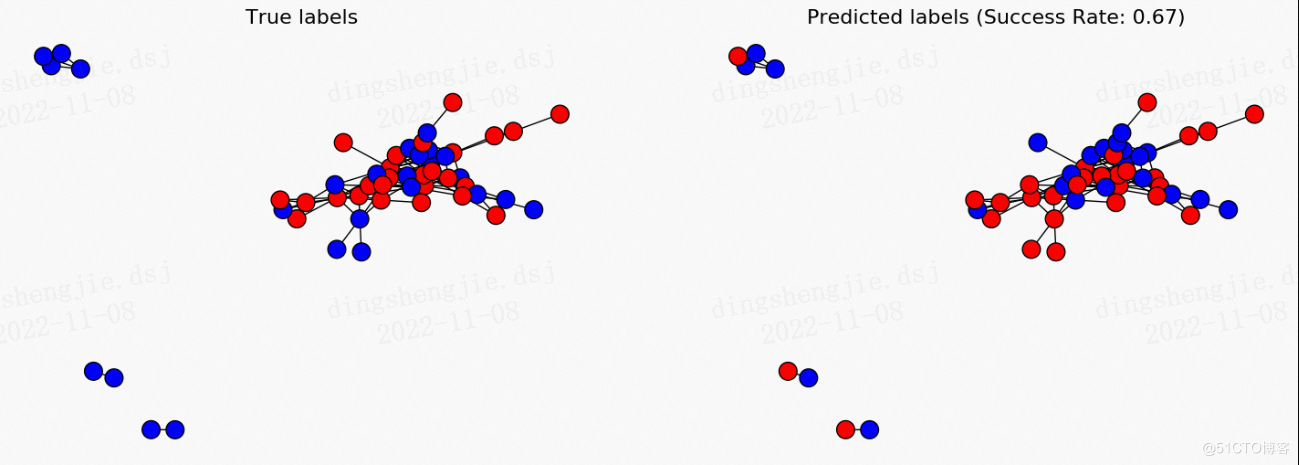
# 為了闡述節點標籤預測是如何進行的,我們首先要刪掉一些節點的標籤,作為要預測的物件。這裡我們只保留了30%的節點標籤:
random.seed(5)
proportion_nodes = 0.3
labeled_nodes = random.sample(G_fb.nodes(), int(proportion_nodes * G_fb.number_of_nodes()))
known_labels = np.zeros(n)
known_labels[labeled_nodes] = labels[labeled_nodes]
plt.figure(figsize=(12,8))
nx.draw(G_fb, cmap = plt.get_cmap('bwr'), nodelist=range(n), node_color = known_labels, node_size=200, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000") # set node border color to black
plt.show()
1.3 圖嵌入(Graph Embedding)
嵌入的學習方式與 word2vec 的 skip-gram 嵌入的學習方式相同,使用的是 skip-gram 模型。問題是,我們如何為 Node2Vec 生成輸入語料庫?資料要複雜得多,即(非)定向、(非)加權、(a)迴圈……
為了生成語料庫,我們使用隨機遊走取樣策略:

在處理NLP或計算機視覺問題時,我們習慣在深度神經網路中對影象或文字進行嵌入(embedding)。到目前為止,我們所看到的圖的一個侷限性是沒有向量特徵。但是,我們可以學習圖的嵌入!圖有不同幾個級別的嵌入:
- 對圖的元件進行嵌入(節點,邊,特徵…)(Node2Vec) node2vec是一個用於圖表示學習的演演算法框架。給定任何圖,它可以學習節點的連續特徵表示,然後可以用於各種下游機器學習任務。

- 對圖的子圖或整個圖進行嵌入(Graph2Vec) Learning Distributed Representations of Graphs
學習圖的分散式表示
最近關於圖結構化資料的表示學習的工作主要集中在學習圖子結構(例如節點和子圖)的分散式表示。然而,許多圖分析任務(例如圖分類和聚類)需要將整個圖表示為固定長度的特徵向量。雖然上述方法自然不具備學習這種表示的能力,但圖核心仍然是獲得它們的最有效方法。然而,這些圖核心使用手工製作的特徵(例如,最短路徑、graphlet 等),因此受到泛化性差等問題的阻礙。為了解決這個限制,在這項工作中,我們提出了一個名為 graph2vec 的神經嵌入框架來學習任意大小圖的資料驅動的分散式表示。圖2vec' s 嵌入是以無監督的方式學習的,並且與任務無關。因此,它們可以用於任何下游任務,例如圖分類、聚類甚至播種監督表示學習方法。我們在幾個基準和大型現實世界資料集上的實驗表明,graph2vec 在分類和聚類精度方面比子結構表示學習方法有顯著提高,並且可以與最先進的圖核心競爭。
1.3.1. 節點嵌入(Node Embedding)
我們首先關注的是圖元件的嵌入。有幾種方法可以對節點或邊進行嵌入。例如,DeepWalk【http://www.perozzi.net/projects/deepwalk/ 】 使用短隨機遊走來學習圖中邊的表示。我們將討論Node2Vec,這篇論文由2016年斯坦福大學的Aditya Grover和Jure Leskovec發表。
作者說:「node2vec是一個用於圖表示學習的演演算法框架。給定任何圖,它可以學習節點的連續特徵表示,然後可以用於各種下游機器學習任務。「
該模型通過使用隨機遊走,優化鄰域保持目標來學習節點的低維表示。
Node2Vec的程式碼可以在GitHub上找到:
https://github.com/eliorc/node2vec
部分程式出圖不一一展示,詳情進入專案連結即可
2.圖神經網路GNN
2.1GNN引言
圖神經網路(Graph Neural Networks,GNN)綜述連結:https://zhuanlan.zhihu.com/p/75307407?from_voters_page=true 譯文
https://arxiv.org/pdf/1901.00596.pdf 原始文章 最新版本V4版本
近年來,深度學習徹底改變了許多機器學習任務,從影象分類和視訊處理到語音識別和自然語言理解。這些任務中的資料通常在歐幾里得空間中表示。然而,越來越多的應用程式將資料從非歐幾里德域生成並表示為具有複雜關係和物件之間相互依賴關係的圖。圖資料的複雜性對現有的機器學習演演算法提出了重大挑戰。最近,出現了許多關於擴充套件圖資料深度學習方法的研究。在本次調查中,我們全面概述了資料探勘和機器學習領域中的圖神經網路 (GNN)。我們提出了一種新的分類法,將最先進的圖神經網路分為四類,即迴圈圖神經網路、折積圖神經網路、圖自動編碼器和時空圖神經網路。我們進一步討論了圖神經網路在各個領域的應用,並總結了圖神經網路的開原始碼、基準資料集和模型評估。最後,我們在這個快速發展的領域提出了潛在的研究方向
神經網路最近的成功推動了圖形識別和資料探勘的研究。許多機器學習任務,如物件檢測 [1]、[2]、機器翻譯 [3]、[4] 和語音識別 [5],曾經嚴重依賴手工特徵工程來提取資訊特徵集,最近已經由各種端到端深度學習範例徹底改變,例如折積神經網路 (CNN) [6]、遞迴神經網路 (RNN) [7] 和自動編碼器 [8]。深度學習在許多領域的成功部分歸功於快速發展的計算資源(例如 GPU)、大訓練資料的可用性以及深度學習從歐幾里得資料(例如影象、文字、和視訊)。以影象資料為例,我們可以將影象表示為歐幾里得空間中的規則網格。折積神經網路 (CNN) 能夠利用影象資料的移位不變性、區域性連通性和組合性 [9]。因此,CNN 可以提取與整個資料集共用的區域性有意義的特徵,用於各種影象分析。
雖然深度學習有效地捕獲了歐幾里得資料的隱藏模式,但越來越多的應用程式將資料以圖形的形式表示。例如,在電子商務中,基於圖的學習系統可以利用使用者和產品之間的互動來做出高度準確的推薦。在化學中,分子被建模為圖形,並且需要確定它們的生物活性以進行藥物發現。在引文網路中,論文通過引文相互連結,並且需要將它們分類到不同的組中。圖資料的複雜性對現有的機器學習演演算法提出了重大挑戰。由於圖可能是不規則的,圖可能具有可變大小的無序節點,並且來自圖中的節點可能具有不同數量的鄰居,導致一些重要的操作(例如折積)在影象域中很容易計算,但是難以應用於圖域。此外,現有機器學習演演算法的一個核心假設是範例相互獨立。這個假設不再適用於圖資料,因為每個範例(節點)通過各種型別的連結(例如參照、友誼和互動)與其他範例相關聯。
最近,人們對擴充套件圖形資料的深度學習方法越來越感興趣。受來自深度學習的 CNN、RNN 和自動編碼器的推動,在過去幾年中,重要操作的新泛化和定義迅速發展,以處理圖資料的複雜性。例如,可以從 2D 折積推廣圖折積。如圖 1 所示,可以將影象視為圖形的特殊情況,其中畫素由相鄰畫素連線。與 2D 折積類似,可以通過取節點鄰域資訊的加權平均值來執行圖折積。

二維折積類似於圖,影象中的每個畫素都被視為一個節點,其中鄰居由過濾器大小確定。 2D 折積取紅色節點及其鄰居畫素值的加權平均值。 節點的鄰居是有序的並且具有固定的大小。
圖折積。 為了得到紅色節點的隱藏表示,圖折積運算的一個簡單解決方案是取紅色節點及其鄰居節點特徵的平均值。 與影象資料不同,節點的鄰居是無序且大小可變的。
發展:
圖神經網路 (GNN) Sperduti 等人的簡史。 (1997) [13] 首次將神經網路應用於有向無環圖,這激發了對 GNN 的早期研究。圖神經網路的概念最初是在 Gori 等人中概述的。 (2005) [14] 並在 Scarselli 等人中進一步闡述。 (2009) [15] 和 Gallicchio 等人。 (2010) [16]。這些早期研究屬於迴圈圖神經網路(RecGNNs)的範疇。他們通過以迭代方式傳播鄰居資訊來學習目標節點的表示,直到達到一個穩定的固定點。這個過程在計算上是昂貴的,並且最近已經越來越多地努力克服這些挑戰[17],[18]。
受 CNN 在計算機視覺領域的成功的鼓舞,大量重新定義圖資料折積概念的方法被並行開發。這些方法屬於折積圖神經網路 (ConvGNN) 的範疇。 ConvGNN 分為兩個主流,基於光譜的方法和基於空間的方法。 Bruna 等人提出了第一個關於基於光譜的 ConvGNN 的傑出研究。 (2013)[19],它開發了一種基於譜圖理論的圖折積。從那時起,基於譜的 ConvGNN [20]、[21]、[22]、[23] 的改進、擴充套件和近似值不斷增加。基於空間的 ConvGNN 的研究比基於光譜的 ConvGNN 早得多。 2009 年,Micheli 等人。 [24] 首先通過架構複合非遞迴層解決了圖相互依賴問題,同時繼承了 RecGNN 的訊息傳遞思想。然而,這項工作的重要性被忽視了。直到最近,出現了許多基於空間的 ConvGNN(例如,[25]、[26]、[27])。代表性 RecGNNs 和 ConvGNNs 的時間線如表 II 的第一列所示。除了 RecGNNs 和 ConvGNNs,在過去幾年中還開發了許多替代 GNN,包括圖自動編碼器 (GAE) 和時空圖神經網路 (STGNN)。這些學習框架可以建立在 RecGNN、ConvGNN 或其他用於圖建模的神經架構上。
綜述總結如下:
-
新分類 我們提出了一種新的圖神經網路分類。圖神經網路分為四組:迴圈圖神經網路、折積圖神經網路、圖自動編碼器和時空圖神經網路。
-
綜合回顧 我們提供了最全面的圖資料現代深度學習技術概覽。對於每種型別的圖神經網路,我們都提供了代表性模型的詳細描述,進行了必要的比較,並總結了相應的演演算法。
-
豐富的資源我們收集了豐富的圖神經網路資源,包括最先進的模型、基準資料集、開原始碼和實際應用。本調查可用作理解、使用和開發適用於各種現實生活應用的不同深度學習方法的實踐指南。
-
未來方向 我們討論了圖神經網路的理論方面,分析了現有方法的侷限性,並在模型深度、可延伸性權衡、異質性和動態性方面提出了四個可能的未來研究方向。
2.2 神經網路型別
在本節中,我們介紹了圖神經網路 (GNN) 的分類,如表 II 所示。 我們將圖神經網路 (GNN) 分為迴圈圖神經網路 (RecGNN)、折積圖神經網路 (ConvGNN)、圖自動編碼器 (GAE) 和時空圖神經網路 (STGNN)。 圖 2 給出了各種模型架構的範例。 下面,我們對每個類別進行簡要介紹。


2.2.1迴圈圖神經網路(RecGNNs,Recurrent graph neural networks )
迴圈圖神經網路(RecGNNs)大多是圖神經網路的先驅作品。 RecGNN 旨在學習具有迴圈神經架構的節點表示。 他們假設圖中的一個節點不斷地與其鄰居交換資訊/訊息,直到達到穩定的平衡。 RecGNN 在概念上很重要,並啟發了後來對摺積圖神經網路的研究。 特別是,基於空間的折積圖神經網路繼承了訊息傳遞的思想。
2.2.2 折積圖神經網路 (ConvGNNs,Convolutional graph neural networks)
折積圖神經網路 (ConvGNNs) 將折積操作從網格資料推廣到圖資料。 主要思想是通過聚合它自己的特徵 xv 和鄰居的特徵 xu 來生成節點 v 的表示,其中 u ∈ N(v)。 與 RecGNN 不同,ConvGNN 堆疊多個圖折積層以提取高階節點表示。 ConvGNN 在構建許多其他複雜的 GNN 模型中發揮著核心作用。 圖 2a 顯示了用於節點分類的 ConvGNN。 圖 2b 展示了用於圖分類的 ConvGNN。
2.2.3圖自動編碼器 (GAE,Graph autoencoders (GAEs))
是無監督學習框架,它將節點/圖編碼到潛在向量空間並從編碼資訊中重建圖資料。 GAE 用於學習網路嵌入和圖形生成分佈。 對於網路嵌入,GAE 通過重構圖結構資訊(例如圖鄰接矩陣)來學習潛在節點表示。 對於圖的生成,一些方法逐步生成圖的節點和邊,而另一些方法一次全部輸出圖。 圖 2c 展示了一個用於網路嵌入的 GAE。
2.2.4 時空圖神經網路 (STGNN,Spatial-temporal graph neural networks)
旨在從時空圖中學習隱藏模式,這在各種應用中變得越來越重要,例如交通速度預測 [72]、駕駛員機動預期 [73] 和人類動作識別 [ 75]。 STGNN 的關鍵思想是同時考慮空間依賴和時間依賴。 許多當前的方法整合了圖折積來捕獲空間依賴性,並使用 RNN 或 CNN 對時間依賴性進行建模。 圖 2d 說明了用於時空圖預測的 STGNN。
具體公式推到見論文!
2.3圖神經網路的應用
GNN 在不同的任務和領域中有許多應用。 儘管每個類別的 GNN 都可以直接處理一般任務,包括節點分類、圖分類、網路嵌入、圖生成和時空圖預測,但其他與圖相關的一般任務,如節點聚類 [134]、連結預測 [135 ],圖分割[136]也可以通過GNN來解決。 我們詳細介紹了基於以下研究領域的一些應用。
計算機視覺(Computer vision)
計算機視覺 GNN 在計算機視覺中的應用包括場景圖生成、點雲分類和動作識別。識別物件之間的語意關係有助於理解視覺場景背後的含義。
場景圖生成模型旨在將影象解析為由物件及其語意關係組成的語意圖 [137]、[138]、[139]。另一個應用程式通過在給定場景圖的情況下生成逼真的影象來反轉該過程 [140]。由於自然語言可以被解析為每個單詞代表一個物件的語意圖,因此它是一種很有前途的解決方案,可以在給定文字描述的情況下合成影象。
分類和分割點雲使 LiDAR 裝置能夠「看到」周圍環境。點雲是由 LiDAR 掃描記錄的一組 3D 點。 [141]、[142]、[143] 將點雲轉換為 k-最近鄰圖或超點圖,並使用 ConvGNN 探索拓撲結構。
識別視訊中包含的人類行為有助於從機器方面更好地理解視訊內容。一些解決方案檢測視訊剪輯中人體關節的位置。由骨骼連線起來的人體關節自然形成了一個圖形。給定人類關節位置的時間序列,[73]、[75] 應用 STGNN 來學習人類動作模式。
此外,GNN 在計算機視覺中的適用方向數量仍在增長。它包括人-物互動[144]、小樣本影象分類[145]、[146]、[147]、語意分割[148]、[149]、視覺推理[150]和問答[151]。
自然語言處理(Natural language processing )
自然語言處理 GNN 在自然語言處理中的一個常見應用是文字分類。 GNN 利用檔案或單詞的相互關係來推斷檔案標籤 [22]、[42]、[43]。
儘管自然語言資料表現出順序,但它們也可能包含內部圖結構,例如句法依賴樹。句法依賴樹定義了句子中單詞之間的句法關係。 Marcheggiani 等人。 [152] 提出了在 CNN/RNN 句子編碼器之上執行的句法 GCN。 Syntactic GCN 基於句子的句法依賴樹聚合隱藏的單詞表示。巴斯廷斯等人。 [153] 將句法 GCN 應用於神經機器翻譯任務。 Marcheggiani 等人。[154] 進一步採用與 Bastings 等人相同的模型。
[153]處理句子的語意依賴圖。
圖到序列學習學習在給定抽象詞的語意圖(稱為抽象意義表示)的情況下生成具有相同含義的句子。宋等人。 [155] 提出了一種圖 LSTM 來編碼圖級語意資訊。貝克等人。 [156] 將 GGNN [17] 應用於圖到序列學習和神經機器翻譯。逆向任務是序列到圖的學習。給定句子生成語意或知識圖在知識發現中非常有用
交通 Traffic
準確預測交通網路中的交通速度、交通量或道路密度對於智慧交通系統至關重要。 [48]、[72]、[74] 使用 STGNN 解決交通預測問題。 他們將交通網路視為一個時空圖,其中節點是安裝在道路上的感測器,邊緣由節點對之間的距離測量,每個節點將視窗內的平均交通速度作為動態輸入特徵。 另一個工業級應用是計程車需求預測。 鑑於歷史計程車需求、位置資訊、天氣資料和事件特徵,Yao 等人。 [159] 結合 LSTM、CNN 和由 LINE [160] 訓練的網路嵌入,形成每個位置的聯合表示,以預測時間間隔內某個位置所需的計程車數量。
推薦系統 Recommender systems
基於圖的推薦系統將專案和使用者作為節點。 通過利用專案與專案、使用者與使用者、使用者與專案之間的關係以及內容資訊,基於圖的推薦系統能夠產生高質量的推薦。 推薦系統的關鍵是對專案對使用者的重要性進行評分。 結果,它可以被轉換為連結預測問題。 為了預測使用者和專案之間缺失的連結,Van 等人。 [161] 和英等人。 [162] 提出了一種使用 ConvGNN 作為編碼器的 GAE。 蒙蒂等人。 [163] 將 RNN 與圖折積相結合,以學習生成已知評級的底層過程
化學 Chemistry
在化學領域,研究人員應用 GNN 來研究分子/化合物的圖形結構。 在分子/化合物圖中,原子被視為節點,化學鍵被視為邊緣。 節點分類、圖分類和圖生成是針對分子/化合物圖的三個主要任務,以學習分子指紋 [85]、[86]、預測分子特性 [27]、推斷蛋白質介面 [164] 和 合成化合物
其他
GNN 的應用不僅限於上述領域和任務。 已經探索將 GNN 應用於各種問題,例如程式驗證 [17]、程式推理 [166]、社會影響預測 [167]、對抗性攻擊預防 [168]、電子健康記錄建模 [169]、[170] ]、大腦網路[171]、事件檢測[172]和組合優化[173]。
2.4未來方向
儘管 GNN 已經證明了它們在學習圖資料方面的能力,但由於圖的複雜性,挑戰仍然存在。
模型深度 Model depth
深度學習的成功在於深度神經架構 [174]。 然而,李等人。 表明隨著圖折積層數的增加,ConvGNN 的效能急劇下降 [53]。 隨著圖折積將相鄰節點的表示推得更近,理論上,在無限數量的圖折積層中,所有節點的表示將收斂到一個點 [53]。 這就提出了一個問題,即深入研究是否仍然是學習圖資料的好策略。
可延伸性權衡 Scalability trade-off
GNN 的可延伸性是以破壞圖完整性為代價的。 無論是使用取樣還是聚類,模型都會丟失部分圖資訊。 通過取樣,節點可能會錯過其有影響力的鄰居。 通過聚類,圖可能被剝奪了獨特的結構模式。 如何權衡演演算法的可延伸性和圖的完整性可能是未來的研究方向。
異質性Heterogenity
當前的大多數 GNN 都假設圖是同質的。 目前的 GNN 很難直接應用於異構圖,異構圖可能包含不同型別的節點和邊,或者不同形式的節點和邊輸入,例如影象和文字。 因此,應該開發新的方法來處理異構圖。
動態Dynamicity
圖本質上是動態的,節點或邊可能出現或消失,節點/邊輸入可能會隨時間變化。 需要新的圖折積來適應圖的動態性。 雖然圖的動態性可以通過 STGNN 部分解決,但很少有人考慮在動態空間關係的情況下如何執行圖折積。
總結
因為之前一直在研究知識提取相關演演算法,後續為了構建小型領域知識圖譜,會用到知識融合、知識推理等技術,現在開始學習研究圖計算相關。
現在已經覆蓋了圖的介紹,圖的主要型別,不同的圖演演算法,在Python中使用Networkx來實現它們,以及用於節點標記,連結預測和圖嵌入的圖學習技術,最後講了GNN應用。
本專案參考了:maelfabien大神、以及自尊心3 在部落格 or github上的貢獻
歡迎大家fork, 後續將開始圖計算相關專案以及部分知識提取技術深化!
專案參考連結:
第一章節:
https://maelfabien.github.io/machinelearning/graph_4/
https://blog.csdn.net/xjxgyc/article/details/100175930
https://maelfabien.github.io/machinelearning/graph_5/
https://github.com/eliorc/node2vec
第二節:
https://zhuanlan.zhihu.com/p/75307407?from_voters_page=true 譯文
https://arxiv.org/pdf/1901.00596.pdf
更多參考:
https://github.com/maelfabien/Machine_Learning_Tutorials
專案連結:https://aistudio.baidu.com/aistudio/projectdetail/4990947?contributionType=1
歡迎fork歡迎三連!文章篇幅有限,部分程式出圖不一一展示,詳情進入專案連結即可