技術文章 » 為什麼你學不會遞迴？談談我的經驗

為什麼你學不會遞迴？談談我的經驗

2022-11-08 21:02:01

本文已收錄到  GitHub · AndroidFamily，有 Android 進階知識體系，歡迎 Star。技術和職場問題，請關注公眾號 [彭旭銳] 進 Android 面試交流群。

前言

大家好，我是小彭。

今天分享到電腦科學中一個基礎又非常重要的概念 —— 遞迴。遞迴是計算機中特有的概念，你很難在現實世界中找到一個恰當的例子與之關聯起來。因此，對於很多初學程式設計的人，一開始會很難理解。

那麼，究竟什麼是遞迴，我們為什麼要使用遞迴？我們今天就圍繞這兩個問題展開。

學習路線圖：

1. 什麼是遞迴？

遞迴（Recursion）是一種通過 「函數自己呼叫自己」 的方式，將問題重複地分解為同類子問題，並最終解決問題的程式設計技巧。

舉個例子，要求一個數 $n$ 的階乘 $n! = n(n-1)(n-2)…2*1$ ，有 2 種思考問題的思路：

  • 遞推（一般思維）： 我們從 $1$ 開始，用 $1$ 乘以 $2$ 得到 $2!$ 問題的解，用 $3$ 乘以 $2!$ 得到 $3!$ 問題的解。依次類推，直到用 $n$ 乘以 $(n-1)!$ 得到原問題 $n!$ 的解。這就是用遞推解決問題，這是相對簡單直接的思考方式；
  • 遞迴（計算機思維）： 我們把 $n!$ 的問題拆分為一個 $(n-1)!$ 的問題，如果我們知道 $(n-1)!$ 的解，那麼將它乘以 $n$ 就可以得出 $n!$ 的解。以此類推，我們將一個 $(n-1)!$ 的問題拆分為同型別的規模更小的 $(n-2)!$ 子問題，直到拆分到無法拆分，可以直接得出結果 $1!$ 問題。此時，我們再沿著拆分問題的路徑，反向地根據子問題的解求出原問題的解，最終得到原問題 $n!$ 的結果。這就是用遞迴解決問題。

求 n!

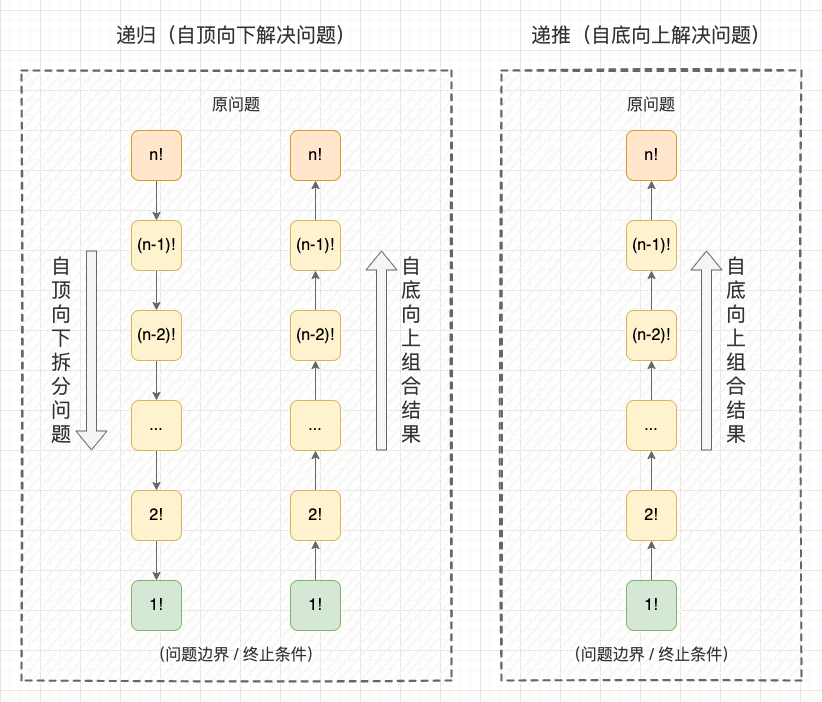
從這個例子可以看出， 遞迴其實是在重複地做 2 件事：

  • 1、自頂向下拆分問題： 從一個很難直接求出結果的、規模較大的原問題開始，逐漸向下拆分為規模較小的子問題（從 $n!$ 拆分到 $(n-1)!$），直到拆分到問題邊界時停止拆分，這個拆分的過程就是 「遞」（問題邊界也叫基準情況或終止條件）；
  • 2、自底向上組合結果： 從問題邊界開始，逐漸向上傳遞並組合子問題的解（從 $(n-1)!$ 得到 $n!$），直到最終回到原問題獲得結果，這個組合的過程就是 「歸」。

看到這裡你會不會產生一個疑問： 我們直接從問題邊界 $1!$ 一層層自底向上組合結果也可以得到 $n!$ 的解，自頂向下拆分問題的過程顯得沒有必要。確實，對於對於這種原問題與子問題只是 「線性」 地減少一個問題規模的情況，確實是這樣。但是對於很多稍微複雜一些的問題，原問題與子問題會構成一個樹型的 「非線性」 結構，這個時候就適合用遞迴解決，很難用遞推解決。

舉個例子， 求斐波那契數列，這個問題同時也是 LeetCode 上的一道典型例題：LeetCode · 509. 斐波那契數：該數列從 $1$ 開始，每一項數位都是前面兩項數位的和。

LeetCode 例題

雖然，我們可以利用遞推的方式從 $F(0)$ 和 $F(1)$ 自底向上推匯出 $F(n)$ 的解，但是這種非線性的方式在程式語言中很難實現，而使用遞迴的方式自頂向下地解決問題，在編碼上是很容易實現的。

當然，這段程式碼中存在非常多的重複計算，最終使得整個演演算法的時間複雜度達到驚人的指數級 $O(2^n)$。例如在計算 $F(5)=F(3)+F(4)$ 和 $F(6)=F(4)+F(5)$ 的時候，$F(4)$ 就被重複計算 2 次，這種重複計算完全相同的子問題的情況就叫 重疊子問題 ，以後我們再專門討論。

用遞迴解決斐波那契數列

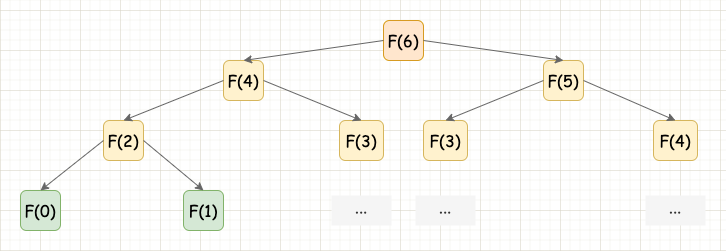
用遞迴解決（無優化）

class Solution {
    fun fib(N: Int): Int {
        if(N == 0){
            return 0
        }
        if(N == 1){
            return 1
        }
        // 拆分問題 + 組合結果
        return fib(N - 1) + fib(N - 2)
    }
}

2. 遞迴的解題模板

  • 1、判斷當前狀態是否異常，例如陣列越界，n < 0 等；
  • 2、判斷當前狀態是否滿足終止條件，即達到問題邊界，可以直接求出結果；
  • 3、遞迴地拆分問題，縮小問題規模；
  • 4、組合子問題的解，結合當前狀態得出最終解。
fun func(n){
    // 1. 判斷是否處於異常條件
    if(/* 異常條件 */){
        return
    }
    // 2. 判斷是否滿足終止條件（問題邊界）
    if(/* 終止條件 */){
        return result
    }
    // 3. 拆分問題
    result1 = func(n1)
    result2 = func(n2)
    ...
    // 4. 組合結果
    return combine(result1, result2, ...)
}

3. 計算機如何實現遞迴？

遞迴程式在解決子問題之後，需要沿著拆分問題的路徑一層層地原路返回結果，並且後拆分的子問題應該先解決。這個邏輯與棧 「後進先出」 的邏輯完全吻合：

  • 拆分問題： 就是一次子問題入棧的過程；
  • 組合結果： 就是一次子問題出棧的過程。

事實上，這種出棧和入棧的邏輯，在程式語言中是天然支援的，不需要程式設計師實現。程式設計師只需要維護拆分問題和組合問題的邏輯，一次函數自呼叫和返回的過程就是一次隱式的函數出棧入棧過程。在程式執行時，記憶體空間中會存在一塊維護函數呼叫的區域，稱為 函數呼叫棧 ，函數的呼叫與返回過程，就天然對應著一次子問題入棧和出棧的過程：

  • 呼叫函數： 程式會建立一個新的棧幀並壓入呼叫棧的頂部；
  • 函數返回： 程式會將當前棧幀從呼叫棧棧頂彈出，並帶著返回值回到上一層棧幀中呼叫函數的位置。

我們在分析遞迴演演算法的空間複雜度時，也必須將隱式的函數呼叫棧考慮在內。

4. 遞迴與迭代的區別

遞迴（Recursion）和迭代（Iteration）都是程式語言中重複執行某一段邏輯的語法。

語法上的區別在於：

  • 迭代： 通過迭代器（for/while）重複執行某一段邏輯；
  • 遞迴： 通過函數自呼叫重複執行函數中的一段邏輯。

核心區別在於解決問題的思路不同：

  • 迭代：迭代的思路認為只要從問題邊界開始，在所有元素上重複執行相同的邏輯，就可以獲得最終問題的解（迭代的思路與遞推的思路類似）；
  • 遞迴：遞迴的思路認為只要將原問題拆分為子問題，在每個子問題上重複執行相同的邏輯，最終組合所有子問題的結果就可以獲得最終問題的解。

例如， 在計算 n! 的問題中，遞推或迭代的思路是從 1! 開始重複乘以更大的數，最終獲得原問題 n! 的解；而遞迴的思路是將 n! 問題拆分為 (n-1)! 的問題，最終通過 (n-1)! 問題獲得原問題 n! 的解。

再舉個例子，面試中出現頻率非常高的反轉連結串列問題，同時也是 LeetCode 上的一道典型例題：LeetCode 206 · 反轉連結串列。假設連結串列為 1 → 2 → 3 → 4 → ∅，我們想要把連結串列反轉為 ∅ ← 1 ← 2 ←3 ←4，用迭代和遞迴的思路是不同的：

  • 迭代： 迭代的思路認為，只要重複地在每個節點上處理同一個邏輯，最終就可以得到反轉連結串列，這個邏輯是：「將當前節點的 next 指標指向前一個節點，再將遊標指標移動到後一個節點」。
  • 遞迴： 遞迴的思路認為，只要將反轉連結串列的問題拆分為 「讓當前節點的 next 指標指向後面整段子鏈的反轉連結串列」，在每個子連結串列上重複執行相同的邏輯，最終就能夠獲得整個連結串列反轉的結果。

這兩個思路用示意圖表示如下：

示意圖

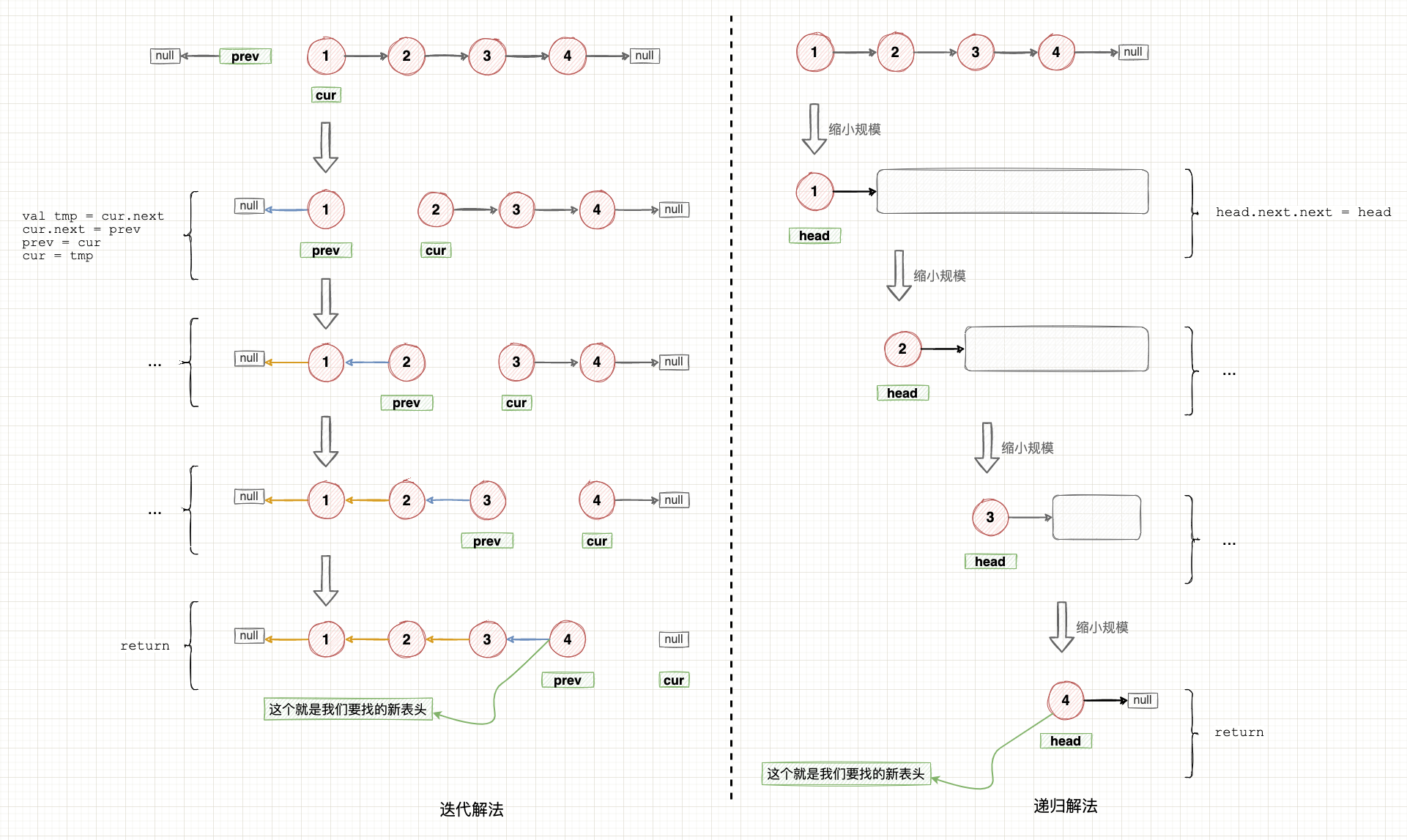
迭代題解

class Solution {
    fun reverseList(head: ListNode?): ListNode? {
        var cur: ListNode? = head
        var prev: ListNode? = null

        while (null != cur) {
            val tmp = cur.next
            cur.next = prev
            prev = cur
            cur = tmp
        }
        return prev
    }
}

迭代解法複雜度分析：

  • 時間複雜度：每個節點掃描一次，時間複雜度為 $O(n)$；
  • 空間複雜度：使用了常數級別變數，空間複雜度為 $O(1)$。

遞迴題解

class Solution {
    fun reverseList(head: ListNode?): ListNode? {
        if(null == head || null == head.next){
            return head
        }
        val newHead = reverseList(head.next)
        head.next.next = head
        head.next = null
        return newHead
    }
}

遞迴解法複雜度分析：

  • 時間複雜度：每個節點掃描一次，時間複雜度為 $O(n)$；
  • 空間複雜度：使用了函數呼叫棧，空間複雜度為 $O(n)$。

理論上認為迭代程式的執行效率會比遞迴程式更好，並且任何遞迴程式（不止是尾遞迴，尾遞迴只是消除起來相對容易）都可以通過一個棧轉化為迭代程式。但是，這種消除遞迴的做法實際上是以犧牲程式可讀性為代價換取的，一般不會為了執行效率而刻意消除遞迴。

不過，有一種特殊的遞迴可以被輕鬆地消除，一些編譯器或執行時會自動完成消除工作，不需要程式設計師手動消除，也不會破壞程式碼的可讀性。

5. 尾遞迴

在程式語言中，尾呼叫是指在一個函數的最後返回另一個函數的呼叫結果。如果尾呼叫最後呼叫的是當前函數本身，就是尾遞迴。為什麼我們要專門定義這種特殊的遞迴形式呢？因為尾遞迴也是尾呼叫，而在大多數程式語言中，尾呼叫可以被輕鬆地消除 ，這使得程式可以模擬遞迴的邏輯而又不損失效能，這叫 尾遞迴優化 / 尾遞迴消除 。例如，以下 2 段程式碼實現的功能是相同的，前者是尾遞迴，而後者是迭代。

尾遞迴

fun printList(itr : Iterator<*>){
    if(!itr.hasNext()) {
        return
    }
    println(itr.next())
    // 尾遞迴
    printList(itr)
}

迭代

fun printList(itr : Iterator<*>){
    while(true) {
        if(!itr.hasNext()) {
            return
        }
        println(itr.next())
    }
}

可以看到，使用一個 while 迴圈和若干變數消除就可以輕鬆消除尾遞迴。

6. 總結

到這裡，相信你已經對遞迴的含義以及遞迴的強大之處有所瞭解。 遞迴是電腦科學中特有的解決問題的思路：先通過自頂向下拆分問題，再自底向上組合結果來解決問題。這個思路在程式語言中可以用函數自呼叫和返回實現，因此遞迴在程式設計實現中會顯得非常簡潔。 正如圖靈獎獲得者尼克勞斯·維爾特所說：「遞迴的強大之處在於它允許使用者用有限的語句描述無限的物件。因此，在電腦科學中，遞迴可以被用來描述無限步的運算，儘管描述運算的程式是有限的。」

另外，你會發現 「先拆分問題再合併結果」 的思想與 「分治思想」 相同，那麼你認為遞迴和分治是等價的嗎？這個我們下回說。

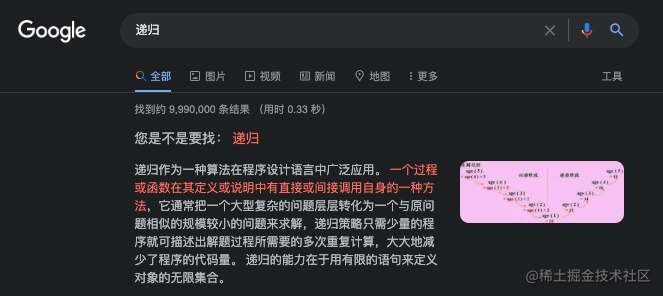
發現一個 Google 的小彩蛋：在 Google 搜尋裡搜尋 「遞迴」，提示詞裡會顯示 「您是不是要找：遞迴」。這就會產生遞迴的效果的，因為點選提示詞 「遞迴」 後，還是會遞迴地顯示 「您是不是要找：遞迴」。哈哈，應該是 Google 跟程式設計師開的小玩笑。

參考資料