MPC:百萬富翁問題
百萬富翁問題

將問題具體化:
Alice有\(i\)億元,Bob有\(j\)億元,為方便描述,我們限定\(0<i, j \leq 10\)。現在想在不暴露和的情況下,比較\(i\)和\(j\)的大小。
解決思路

⚠️
第二步:Bob把第\(j\)個箱子上的編號撕掉,並將其他箱子都銷燬掉,把這個沒有編號的箱子發給Alice
以上是解決百萬富翁問題的思路之一,但是建立在雙方都是誠實的或者半誠實的前提下,即雙方不會惡意的輸入或者輸出錯誤值擾亂協定的正確執行,也就是說可以保證Bob不會選擇錯誤的箱子或者將錯誤的箱子傳送給Alice,但是無法保證Bob能剋制住自己的好奇心,將其他的箱子都銷燬掉,因為即使Bob不銷燬其他的箱子,協定也能正常執行,符合一個半誠實參與方的要求。
在實際應用中,雙方使用密碼協定實現這些理想的限制條件,即即使是半誠實的參與方,協定也不會洩露隱私。比如OT,可以保證Bob只能選一個箱子,而不能獲取其他箱子的內容,同時Alice也無法得知Bob選的是哪個箱子。
下面給出其他的方式解決以上問題
OT
對於百萬富翁問題存在的隱患,即確認Bob是否會將其與的箱子銷燬是一個很難解決的問題。OT可以解決該問題,可以避免Bob未按照協定銷燬其他箱子而產生的安全問題。
直觀上看,OT協定只能保證Bob從Alice準備的10個箱子中選擇一個,而得不到其他箱子(其他資訊),同時還能保證Alice不知道Bob選擇了哪個箱子。
所以這裡符合\((1-n)\)OT,即\(n\)取\(1\),下面用一個例子介紹方案的思想:
-
Alice在鎖上箱子前,Bob先利用所需箱子的編號\(j\)構造一把「複雜」的組合鑰匙(可以看做\(OPRF(j)\)),將其傳送給Alice;
-
Alice拿到組合鑰匙後,通過一種黑盒的方式對組合鎖進行改造,生成10把不同的新鎖,並分別對10個箱子進行上鎖;【新鎖的特性是隻有編號為\(j\)的箱子上的新鎖可以用Bob的組合鑰匙開啟,其餘箱子上的新鎖無法被開啟】;
-
Bob只能開啟編號為\(j\)的箱子,而Alice並不能根據組合鑰匙分析出編號\(j\)。
換成具體協定\((1-n)-OT\)表示:
- 雙方協商出公引數:\(g,h\),都是\(q\)階迴圈群\(G_q\)中的元素
- Alice輸入\(n\)個訊息\(m_1,...,m_n\in G_q\),同時Bob確定選擇的訊息編號\(t\)
- Bob選擇亂數\(r\),計算\(y=g^rh^t\),並將其傳送給Alice
- Alice選擇一組亂數\(k_i\),計算\(n\)組訊息:\((a_i,b_i)\),並行送給Bob,其中\(a_i=g^{k_i},b_i=m_i*(\frac{y}{h_i})^{k_i}\)
- Bob計算出\(m_t=\frac{b_t}{a_t^r}\)
⚠️:
- 其中\(y\)就是組合鑰匙,\((a_i,b_i)\)就是新鎖
- 通過OT協定可以實現Bob只能獲取編號為\(j\)的箱子,對其他的箱子一無所知,且Alice也不知道Bob選擇的哪個箱子,這樣其他箱子銷燬與否無關緊要,從而避免了以上說的安全問題。
GC
混淆電路是姚針對百萬富翁問題在1986年提出的一種解決方案,同時也驗證了安全多方計算的可行性,即百萬富翁問題就是MPC的一個簡單例子,即參與方在不洩漏自身資料的情況下完成某種計算,下面介紹利用混淆電路實現該功能!
混淆電流的思路是將雙方需要計算的函數轉換為「加密電路」,其中「加密電路」可以保證雙方在不洩漏各自輸入資訊的情況下,正確的計算函數的結果。
混淆電路的核心就是「加密電路」設計,這是研究重點和難點,由於任意函數理論上都存在一個等價的電路表示,在計算機中可以使用加法器和乘法器實現,而乘法器/加法器可以通過「與門」、」互斥或門「等邏輯電路來表示。
下面介紹一種」與門「函數實現加密電路:
假設在安全兩方計算中,參與方A和B要計算」與門「的閘電路,即兩者輸入分別是\(a,b\),輸出是\(r=a(and)b\):
- 下表是「與門」真值表
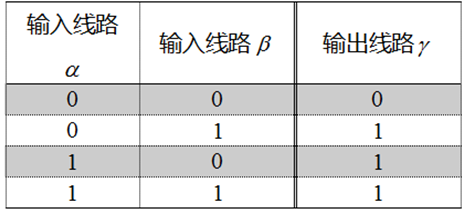
- 第一步,Alice金鑰生成:對輸入和輸出的每個值都生成對應的金鑰,在互動過程中使用該金鑰替換真實值進行傳輸,從而避免真實資料的洩露。

- 第二步,Alice進行電路加密(就是替換):對原始真值表真實的輸入和輸出資料進行替換得到加密版本:
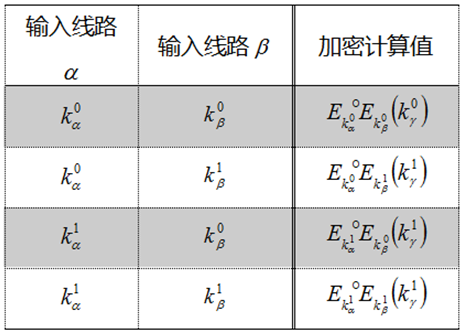
- 第三步,Alice將輸出的密文傳送給Bob:Alice將第二步得到密文\(E_{k_{aj},k_{bi}}(k_{rt})\)打亂資料【混淆】之後傳送給Bob,同時告知Bob\(k_{aj},k_{bi}\)的資訊,讓Bob解密。其中\(k_{aj}\)對應Alice的輸入資料\(a\),\(k_{bi}\)對應於Bob的輸入資料,但由於Alice不知道Bob的真實輸入資料,便無法確定應該向Bob提供\(k_{b0}\)還是\(k_{b1}\),這是便可以使用OT,既能保證Bob根據自己的輸入資料\(b\)的編號\(i\)對應的\(k_bi\),又能保證Bob只能獲得\(k_{b0}\)和\(k_{b1}\)中的一個。
- 第四步,Bob解密:Bob使用Alice提供的\(k_{aj}\)和OT協定選出的\(k_{bi}\)對四個密文解密,其中只有密文是\(E_{k_{aj},k_{bi}}(k_{rt})\)時才能正確解密,否則得到的是亂碼。然後Bob將解密結果發給Alice,Alice得到正確結果\(r=0\)或者\(r=1\),並同步給Bob。
⚠️:
- 整個過程,Alice沒有告訴Bob關於\(k_{aj}\)對應的真實值,Bob通過OT得到了\(k_{bi}\),也沒有洩露資訊,所以雙方在均未洩漏資料的前提下完成了「與門」計算
SS
SS也能構造MPC,下面介紹使用SS構造實現加法和乘法運算:
加法
假設某公司的 3 個員工分別為 \(P_1, P_{2}, P_{3}\),3 人希望在不洩露自己真實工資的情況下, 計算3人的平均工資。
從本質上來講, 這個問題可以抽象為多方之間的求和問題,我們在此介紹一下使用祕密分享進行求和的思想。
假設員工\(P_{1}, P_{2}, P_{3}\) 的工資分別為\(x, y, z\) ,為了計算\(r=(x+y+z) / 3\) , 可以採取以下兩個步驟:
- 祕密分享階段。每個員工將自己的輸入資訊 (即工資) 切分成3份, 並分發給另外兩個同事; 在分發完成之後, 員工$ P_{i}$ 擁有 3 個值, 分別為 $x_{i}, y_{i}, z_{i} $。
- 祕密重構階段。每個員工分別在本地計算 $ r_{i}=\left(x_{i}+y_{i}+z_{i}\right) / 3$ ,最終三個 員工再將自己的結果 $r_{i} $進行公開, 3 人的平均工資則為 $ r=r_{1}+r_{2}+r_{3}$ 。
在以上兩個步驟中, 每個員工都只得到了同事工資的部分資訊, 並不能恢復其真實工資。另外, 根據最終公佈的結果$ r_{i}$ 也無法直接推斷出\(x_{i}, y_{i}, z_{i}\) 三個碎片信 息。因此,該方法便使用祕密分享的思想,在保護了各個參與方輸入資訊的前提下完成均值計算。
乘法
假設員工\(P_{1}, P_{2}, P_{3}\) 的工資分別為\(x, y, z\) ,為了計算\(r=xyz\) 。
而對於乘法計算,就比較複雜了,因為乘法會涉及交叉項,例如\(xy=(x_1+x_2)(y_1+y_2)=x_1y_1+x_1y_2+x_2y_1+x_1y_2\),其中直接計算\(x_1y_2,x_2y_1\)是非常麻煩的【因為資訊屬於兩個人】,這時就需要引入一些輔助資訊:
- 三元組生成和分發,即\(P_1\)有\(a_1,b_1,c_1\),\(P_2\)有\(a_2,b_2,c_2\),\(P_3\)有\(a_3,b_3,c_3\)。
\(\begin{array}{l} a=a_{1}+a_{2}+a_{3} \\ b=b_{1}+b_{2}+b_{3} \\ c=c_{1}+c_{2}+c_{3} \end{array}\)
其中\(c=ab\)。
- 密祕分發,即將\(x,y\)分發,得到以下結果:
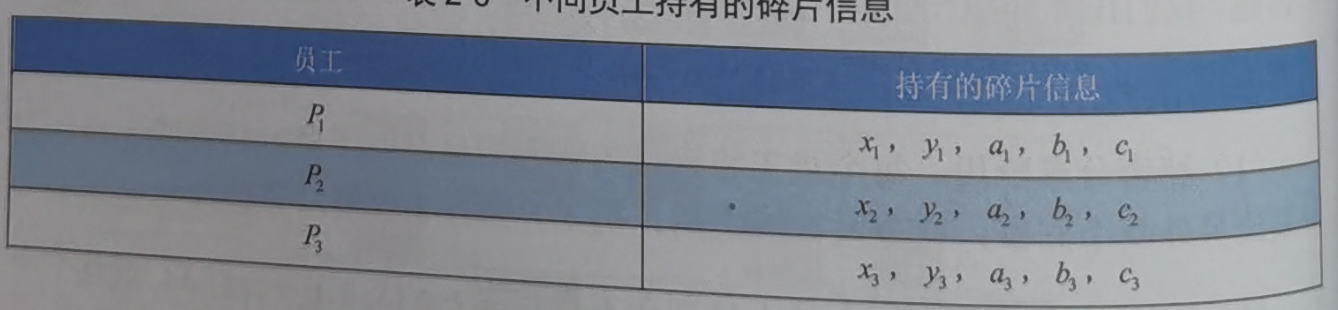
- 祕密重構
(1)藉助輔助資訊,先計算出:\(ma=x-a,mb=y-b\),即利用上述加法特性,以\(x-a\)為例:三方共用計算\(x_1-a_1,x_2-a_2,x_3-a_3\),然後得到\(x-a\)
(2)計算\(xy=(x-a+a)(y-b+b)=(m a+a)(m b+b)=m a \cdot m b+m a \cdot b+m b \cdot a+c\),可以看出將\(xy\)問題轉化為三個乘法問題和加法問題,其中\(ma,mb\)已經得到,因此只需各方計算出\(ma.b+mb.a+c\)的碎片即可:

(3)然後將\(ma.b+mb.a+c\)與\(ma.mb\)相加,便可以得到\(xy\),進而通過這種方法求出\(xyz\)。
⚠️:
- SS的乘法需要使用輔助資訊三元組,在加法和乘法基礎上,可以組合出更加複雜的運算,構造出更加完整、通用的MPC協定。
- GC構造的MPC更適合於邏輯運算或數位的比較運算,比如百萬富翁問題。
- SS構造的MPC更適用於算術運算。
姚期智院士在提出「百萬富翁問題」的同時,給出了三種解決辦法【OT、GC、SS?】,並討論了在祕密投票(Secret Vote)、不經意協商(Oblivious Negotiation)、隱私查詢資料庫(Private Querying of Database)的應用。
之後 Goldreich 在1987年對安全多方計算(Secure Multi-Party Computation)進行了討論,提出了可以計算任意函數的計算意義下安全的安全多方計算協定。Goldreich 還從理論上證明了可以通過通用電路(Universal Circuit)估值來實現所有的安全多方計算協定。其後於1988年,Goldreich 對安全多方計算進行了總結和安全性定義。
之後在 1989 年,Beaver 等人研究了資訊理論安全模型下的安全多方科學計算問題,提出了可以實現資訊理論安全的,複雜程度為常數輪的安全多方算數運算協定。
應用
安全多方計算兼具理論研究和實際應用價值,在電子投票、隱私保護的資料探勘、機器學習、區塊鏈、生物資料比較、雲端計算等領域有著廣泛的應用前景。
- 電子投票
現實生活中的投票選舉通過統一採用空白選票、投票箱、有公信力的計票人以及全程錄影直播等方式來確保公平公正。而在電子投票領域,投票人在家投票時,家中的計算機可能已被感染病毒,投票結果可能被惡意獲取篡改等,因此電子投票系統必須保證投票人知道自己的投票資訊是否被正確提交,是否被惡意攻擊者篡改,同時要保護投票人的投票資訊不被除了計票人外的其他人獲取。安全多方計算為這種分散式環境下如何進行保護隱私資訊和確保結果正確性的問題提供了良好解決方案。
Cramer 等人基於 ElGamal 門限加密技術和零知識證明提出了首個多選一電子投票方案,之後 Damgard 等人基於 Pailier 同態加密技術提出了多選多的電子投票方案。在1992年,A.Fujioka 等使用盲簽名技術提出了著名的 FOO 電子投票協定。
- 資料探勘
資料探勘作為一個非常有效的資料分析工具,可以發現資料中隱含的規律,對科學和政策研究、商務決策等方面有著重要應用。然而被挖掘的資料中往往都有著大量敏感性的資訊,因此必須受到保護,在隱私保護下進行資料探勘。
在多方情況下進行資料探勘時,參與者往往不願意共用資料,只願意共用資料探勘的結果,這種情況在科學和醫學研究等方面非常常見,如各個醫療機構的病人資訊是敏感資訊,不會願意透露。應用安全多方計算可以在保護各方資料資訊不被洩露的同時多方共同作業完成資料探勘。

- 模型訓練
機器學習已被應用到各個領域,引發了大量變革,如影象和語音識別、異常檢測等。而在機器學習想要取得好的效果,需要大量資料進行模型訓練,訓練資料的隱私保護同樣是問題,在多個機構合作進行模型訓練時,資料分佈在不同參與者處,安全多方計算可以在保護敏感資料的隱私性的同時讓各個機構成功進行模型訓練。
總之,當各個參與者處於分散式環境下,又有資料隱私保護的要求時,十分適合應用安全多方計算來解決問題。
參考
1、聯邦學習-技術及實踐