二元樹中查詢後繼節點問題

作者：Grey

原文地址：

部落格園：二元樹中查詢後繼節點問題

CSDN：二元樹中查詢後繼節點問題

題目描述

給定一個二叉查詢樹，以及一個節點，求該節點在中序遍歷的後繼，如果沒有則返回 null

題目連結見：LintCode 448 · Inorder Successor in BST

思路一，利用中序遍歷遞迴解法，使用 List 收集中序遍歷的節點，然後遍歷一遍 List，找到給定節點的下一個節點即可，中序遍歷的遞迴方法程式碼很簡單，參考二元樹的先，中，後序遍歷(遞迴，非遞迴)。

完整程式碼如下

public class Solution {

    public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        List<TreeNode> ans = new ArrayList<>();
        if (root == null) {
            return null;
        }
        in2(root, ans);
        boolean find = false;
        for (TreeNode c : ans) {
            if (c == p) {
                find = true;
            } else if (find) {
                return c;
            }
        }
        return null;
    }

    private static void in2(TreeNode root, List<TreeNode> ans) {
        if (root == null) {
            return;
        }
        in2(root.left, ans);
        ans.add(root);
        in2(root.right, ans);
    }
}

時間複雜度 O(N)，空間複雜度 O(N)。

同樣，中序遍歷可以使用迭代方法來寫，思路和遞迴方法一樣，標記遍歷到的節點 p，然後設定已遍歷的標誌位，如果標誌位設定過，則下一個遍歷到的元素就是後繼節點。

完整程式碼如下，核心就是把中序遍歷的遞迴解改成迭代

public class Solution {
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        if (root == null) {
            return null;
        }
        boolean flag = false;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (!stack.isEmpty() || cur != null) {
            if (cur != null) {
                stack.push(cur);
                cur = cur.left;
            } else {
                cur = stack.pop();
                if (cur == p) {
                    // 遍歷到當前位置，記錄一下
                    flag = true;
                } else if (flag) {
                    // 下一次遍歷的位置，就是後繼節點
                    return cur;
                }
                cur = cur.right;
            }
        }
        return null;
    }
}

思路二，使用 Morris 遍歷實現中序遍歷，這樣可以讓空間複雜度達到 O(1)，時間複雜度依舊 O(N)。Morris 遍歷的內容參考：Morris 遍歷實現二元樹的遍歷。完整程式碼如下

public class Solution {
    public TreeNode inorderSuccessor(TreeNode head, TreeNode p) {
        if (head == null) {
            return null;
        }
        TreeNode ans = null;
        TreeNode cur = head;
        TreeNode mostRight;
        boolean find = false;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                }
            }
            if (find) {
                ans = cur;
                find = false;
            }
            if (cur == p) {
                find = true;
            }
            cur = cur.right;
        }
        return ans;
    }
}

思路三，

利用二元搜尋樹的特性，如果目標節點的右孩子不為空，則目標節點右樹最左節點就是目標節點的後繼節點，範例如下

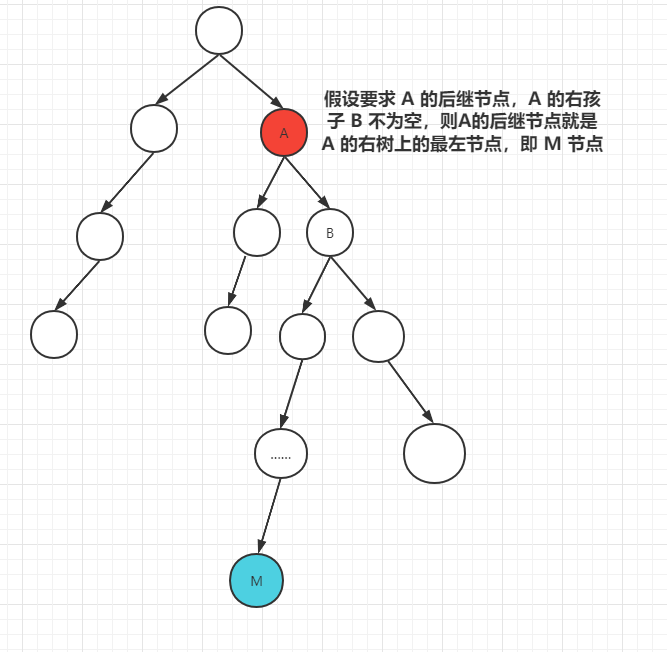
如果目標節點右孩子為空，則只需要找第一個大於目標節點值的節點即可，根據二元搜尋樹的性質，每個節點的右孩子都比當前節點值大，每個節點的左孩子都比當前節點值小。

在遍歷過程中，

如果當前節點的值大於目標節點的值，則先記錄下當前節點（有可能是備選答案，但是不確定有沒有更接近目標值的選擇），然後遍歷的節點往左邊移動，

如果當前節點的值小於目標節點的值，一定不是後繼，遍歷的節點往右邊移動。

如果當前節點的值等於目標節點的值，說明一定找到了後繼（因為這個過程中可以確定當前節點沒有右孩子，所以，到這一步，肯定是通過後繼過來的，或者後繼為 null），直接 break 即可。

空間複雜度O(1)，時間複雜度O(h)，其中 h 為二元樹的高度。

完整程式碼如下

public class Solution {
        public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        if (p == null) {
            return null;
        }
        if (p.right != null) {
            return rightLeftMost(p.right);
        }
        TreeNode successor = null;
        while (root != null) {
            if (root.val > p.val) {
                successor = root;
                root = root.left;
            } else if (root.val < p.val) {
                root = root.right;
            } else {
                break;
            }
        }
        return successor;
    }

    private static TreeNode rightLeftMost(TreeNode p) {
        while (p.left != null) {
            p = p.left;
        }
        return p;
    }
}

演演算法和資料結構筆記

二元樹中查詢後繼節點問題

二元樹中查詢後繼節點問題

題目描述

更多