謠言檢測(SRD-PSCD)《Rumor Detection with Self-supervised Learning on Texts and Social Graph》
論文資訊
論文標題:Rumor Detection with Self-supervised Learning on Texts and Social Graph
論文作者:Yuan Gao, Xiang Wang, Xiangnan He, Huamin Feng, Yongdong Zhang
論文來源:2202,arXiv
論文地址:download
論文程式碼:download
1 Introduction
出發點:考慮異構資訊;
本文的貢獻描述:看看就行...............................
2 Methodology

模組:
(1) propagation representation learning, which applies a GNN model on the propagation tree;
(2) semantic representation learning, which employs a text CNN model on the post contents;
(3) contrastive learning, which models the co-occurring relations among propagation and semantic representations;
(4) rumor prediction, which builds a predictor model upon the event representations.
2.1 Propagation Representation Learning
考慮結構特徵
對於貼文特徵編碼:
$\mathbf{H}^{(l)}=\sigma\left(\mathbf{D}^{-\frac{1}{2}} \hat{\mathbf{A}} \mathbf{D}^{-\frac{1}{2}} \mathbf{H}^{(l-1)} \mathbf{W}^{(l)}\right)\quad\quad\quad(2)$
貼文圖級表示:
$\mathbf{g}=f_{\text {mean-pooling }}\left(\mathbf{H}^{(L)}\right)\quad\quad\quad(3)$
2.2 Semantic Representation Learning
首先:在貼文特徵上使用多頭注意力機制得到初始詞嵌入 $\mathbf{Z} \in \mathbb{R}^{l \times d_{\text {model }}}$ ($l$ 代表著貼文數,$d_{\text {model }}$ 代表貼文的維度):
$\boldsymbol{Z}_{i}=f_{\text {attention }}\left(\boldsymbol{Q}_{i}, \boldsymbol{K}_{i}, \boldsymbol{V}_{i}\right)=f_{\text {softmax }}\left(\frac{\boldsymbol{Q}_{i} \boldsymbol{K}_{i}^{T}}{\sqrt{d_{k}}}\right) \boldsymbol{V}_{i}\quad\quad\quad(4)$
$\boldsymbol{Z}=f_{\text {multi-head }}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=f_{\text {concatenate }}\left(\boldsymbol{Z}_{1}, \ldots, \boldsymbol{Z}_{h}\right) \boldsymbol{W}^{O}\quad\quad\quad(5)$
接著:使用 CNN 進一步提取文字資訊
考慮感受野大小為 $h$ ,得到 feature vector $\boldsymbol{v}_{i}$
$\boldsymbol{v}_{i}=\sigma\left(\boldsymbol{w} \cdot \boldsymbol{z}_{i: i+h-1}+\boldsymbol{b}\right)\quad\quad\quad(6)$
在 sentence 中遍歷,得到詞向量集合:
$\boldsymbol{v}=\left[\boldsymbol{v}_{1}, \boldsymbol{v}_{2}, \ldots, \boldsymbol{v}_{n-h+1}\right]$
在詞向量集合 $\boldsymbol{v}$ 採用 max-pooling 得到全域性表示 $\hat{\boldsymbol{v}}\quad\quad\quad(7)$:
$\hat{\boldsymbol{v}}=f_{\text {max-pooling }}(\boldsymbol{v})\quad\quad\quad(8)$
考慮使用 $n$ 個 feature map ,並拼接表示得到文字表示 $\mathbf{t}$:
$\mathbf{t}=f_{\text {concatenate }}\left(\hat{\boldsymbol{v}}_{1}, \hat{\boldsymbol{v}}_{2}, \ldots, \hat{\boldsymbol{v}}_{n}\right)\quad\quad\quad(4)$
2.3 Contrastive Learning
本文認為同一貼文的基於結構的表示 $\boldsymbol{g}_{i}$ 和基於語意 $\boldsymbol{t}_{i}$ 的表示是正對:
2.3.1 Propagation-Semantic Instance Discrimination (PSID)
${\large \mathcal{L}_{\mathrm{ssl}}=\sum\limits_{i \in C}-\log \left[\frac{\exp \left(s\left(\boldsymbol{g}_{i}, \boldsymbol{t}_{i}\right) / \tau\right)}{\sum\limits _{j \in C} \exp \left(s\left(\boldsymbol{g}_{i}, \boldsymbol{t}_{j}\right) / \tau\right)}\right]} \quad\quad\quad(10)$
2.3.2 Propagation-Semantic Cluster Discrimination (PSCD)
聚類級對比學習:
$\begin{array}{l}\underset{\mathbf{S}_{G}}{\text{min}}\quad \sum\limits _{c \in C} \underset{\mathbf{a}_{1}}{\text{min}} \left\|E_{1}(\mathbf{g})-\mathbf{S}_{G} \mathbf{a}_{1}\right\|_{2}^{2}+\underset{\mathbf{S}_{T}}{\text{min}} \sum\limits _{c \in C} \underset{\mathbf{a}_{2}}{\text{min}} \left\|E_{2}(\mathbf{t})-\mathbf{S}_{T} \mathbf{a}_{2}\right\|_{2}^{2}\\\text { s.t. } \quad \mathbf{a}_{1}^{\top} \mathbf{1}=1, \quad \mathbf{a}_{2}^{\top} \mathbf{1}=1\end{array}\quad\quad\quad(11)$
-
- $\mathbf{S}_{G}\in \mathbb{R}^{d \times K}$ 和 $\mathbf{S}_{T} \in \mathbb{R}^{d \times K}$ 分別代表了 基於結構資訊和基於語意資訊的可訓練質心矩陣;
- $\mathbf{a}_{1}\in\{0,1\}^{K}$ 和 $\mathbf{a}_{2} \in\{0,1\}^{K}$ 代表了聚類分配;
- $E_{1}$ 和 $E_{2}$ 代表了編碼器;
$\mathcal{L}_{\mathrm{ssl}}=\sum\limits _{c \in C} l\left(f_{1}\left(E_{1}(\mathbf{g})\right), \mathbf{a}_{2}\right)+l\left(f_{2}\left(E_{2}(\mathbf{t})\right), \mathbf{a}_{1}\right) \quad\quad\quad(12)$
其中,$l(\cdot)$ 是 negative log-softmax function $l(\cdot) = -\operatorname{LogSoftmax}\left(x_{i}\right)=\log \left(\frac{\exp \left(x_{i}\right)}{\sum\limits _{j} \exp \left(x_{j}\right)}\right)$,$f_{1}(\cdot)$ 、$f_{2}(\cdot)$是一個可訓練的分類器。
PSCD 和 PSID 的處理過程如 Figure 3 :
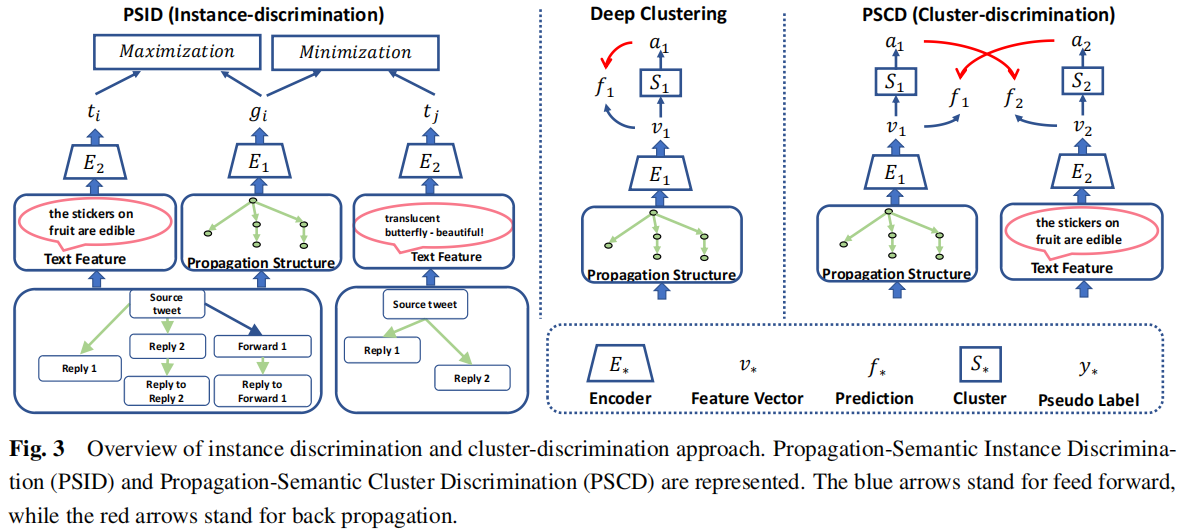
2.4 Rumor Prediction
$p(c)=\sigma(\mathbf{W} \mathbf{g}+\mathbf{b})\quad\quad\quad(13)$

3 Experiments and Analyses
3.1 Dataset
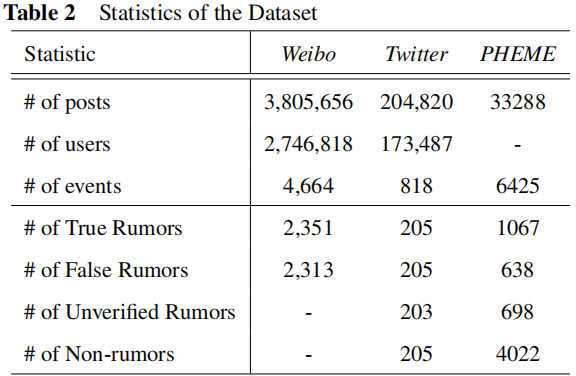
3.2 Result
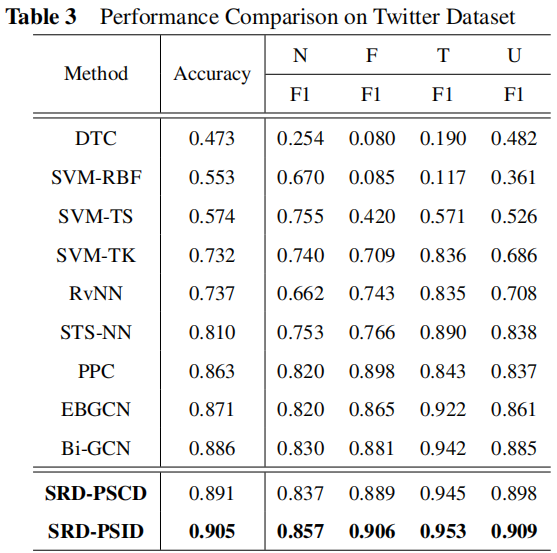
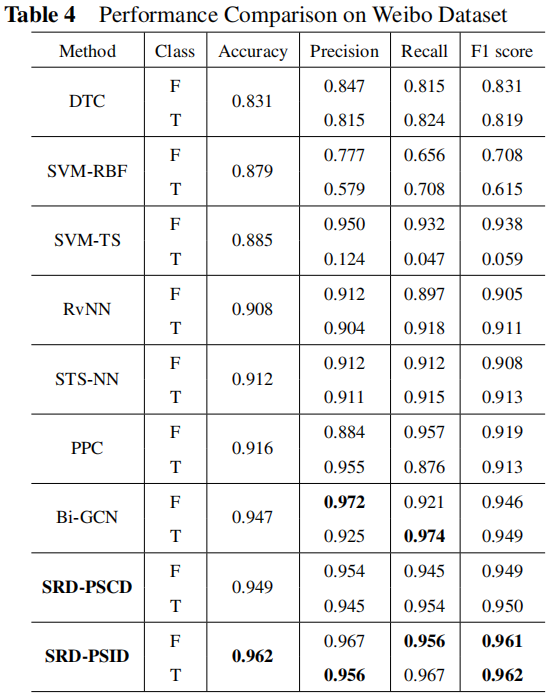
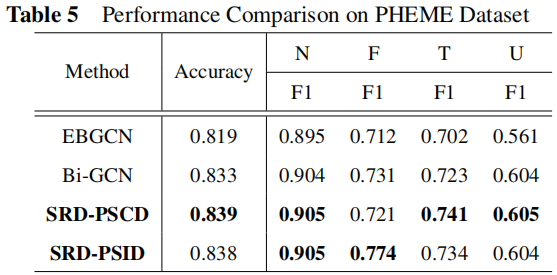
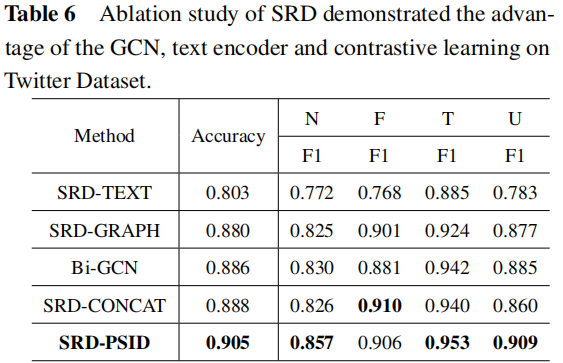
3.3 Ablation Analysis

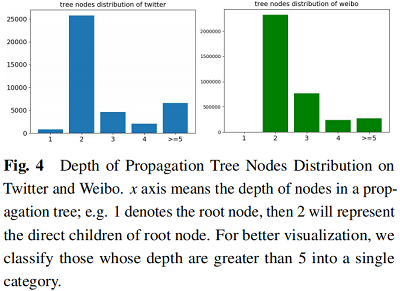
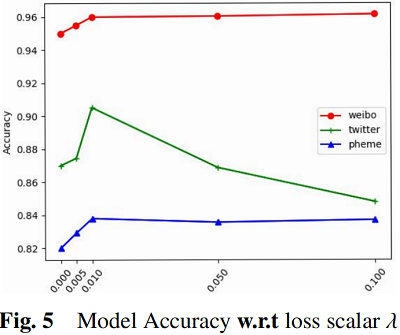
因上求緣,果上努力~~~~ 作者:視界~,轉載請註明原文連結:https://www.cnblogs.com/BlairGrowing/p/16860457.html