1 導引

在上一篇部落格《圖資料探勘：網路中的級聯行為》中介紹了用基於決策的模型來對級聯行為進行建模，該模型是基於效用(Utility)的且是是確定性的，主要關注於單個節點如何根據其鄰居的情況來做決策，需要大量和資料相關的先驗資訊。這篇部落格就讓我們來介紹基於概率的傳播模型，這種模型基於對資料的觀測來構建，不過不能對因果性進行建模。

2 基於隨機樹的流行病模型

接下來我們介紹一種基於隨機樹的傳染病模型，它是分支過程（branching processes）的一種變種。在這種模型中，一個病人可能接觸\(d\)個其他人，對他們中的每一個都有概率\(q>0\)將其傳染，如下圖所示：

接下來我們來看當\(d\)和\(q\)取何值時，流行病最終會消失（die out），也即滿足

\[\lim _{h \rightarrow \infty} p_h=0 \]

這裡\(p_h\)為在深度\(h\)處存在感染節點的概率（是關於\(q\)和\(d\)的函數）。如果流行病會永遠流行下去，則上述極限應該\(>0\)。

\(p_h\)滿足遞迴式：

\[p_h=1-\left(1-q \cdot p_{h-1}\right)^d \]

這裡\(\left(1-q \cdot p_{h-1}\right)^d\)表示在距離根節點\(h\)深度處沒有感染節點的概率。

接下來我們通過對函數

\[f(x)=1-(1-q \cdot x)^d \]

進行迭代來得到\(\lim _{h \rightarrow \infty} p_h\)。我們從根節點\(x=1\)(因為\(p_1=1\))開始，依次迭代得到\(x_1=f(1), x_2=f(x_1),x_3=f(x_2)\)。事實上，該迭代最終會收斂到不動點\(f(x)=x\)，如下圖所示：

這裡\(x\)是在深度\(h-1\)處存在感染節點的概率，\(f(x)\)是在深度為\(h\)處存在感染節點的概率，\(q\)為感染概率，\(d\)為節點的度。
如果我們想要傳染病最終消失，那麼迭代\(f(x)\)的結果必須要趨向於\(0\)，也即不動點需要為0。而這也就意味著\(f(x)\)必須要在\(y=x\)下方，如下所示：

如何控制\(f(x)\)必須要在\(y=x\)下方呢？我們先來分析下\(f(x)\)的影象形狀，我們有以下結論：

\(f(x)\)是單調的：對\(0 \leq x, q \leq 1, d>1\)，\(f'(x)=q \cdot d(1-q x)^{d-1}>0\)，故\(f(x)\)是單調的。

\(f'(x)\)是非增的：\(f'(x)=q \cdot d(1-q x)^{d-1}\)會著\(x\)減小而減小。

而\(f(x)\)低於\(y=x\)，則需要滿足

\[f'(0)=q\cdot d<1 \]

綜上所述，我們有結論：

\[\lim _{h \rightarrow \infty} p_h=0 \text { when } q \cdot d<\mathbf{1} \]

這裡\(R_0=q\cdot d\)表示每個被感染的個體在期望意義上所產生的新的病體數，我們將其稱為基本再生數（reproductive number），它決定了傳染病病是否會流行：

若\(R_0\geq 1\): 流行病永遠不會消失且感染人數會以指數速度上升。
若\(R_0\leq 1\): 流行病會以指數速度快速消失。

3 SIR與SIS流行病模型

3.1 模型正規化

在病毒的傳播中，有兩個最基本的引數：

出生率\(\beta\) 被已感染鄰居攻擊的概率
死亡率\(\delta\) 已感染節點治癒的概率

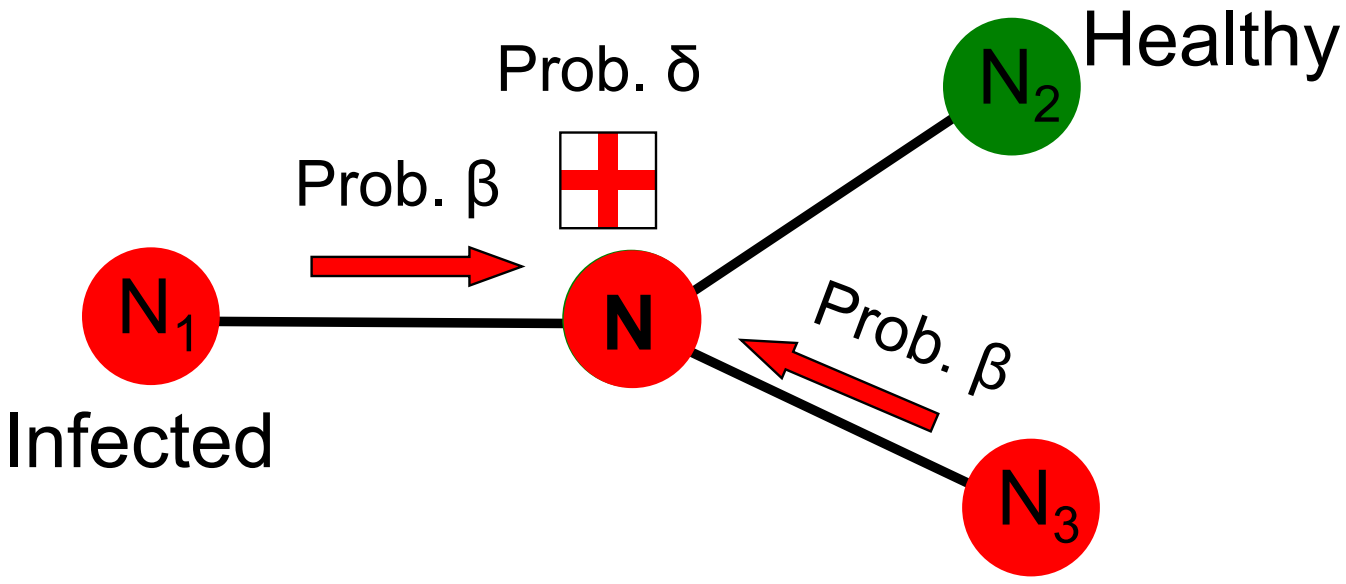
網路中的節點可以在以下四個狀態（S+E+I+R）之間做轉移：

易感期(susceptible)：節點患病之前，處於容易被鄰居傳染的時期，也稱敏感期。
潛伏期(exposed)：節點已被感染，但是還沒具備能力去傳染別人。
傳染期(infectious)：節點已被感染，且能夠以一定的概率把疾病傳染給那些處於易感期的鄰居，也稱感染期。
移除期(removed)：當一個節點經歷了完整的傳染期，就不再被考慮了，因為它不會再受感染，也不會對其它節點構成威脅，也稱隔離期。

狀態轉移圖如下圖所示（圖中的\(Z\)表示人工免疫）：

其中狀態轉移的概率由我們前面提到的模型引數\(\beta\)和\(\delta\)控制。

3.2 SIR模型

在SIR模型中，節點經歷S-I-R三個階段：
遷移學習和多工學習之間的區別
事實上，該模型可用於對水痘和鼠疫的建模，也即一旦我治癒了，那我就永遠不會再被感染了。

假設模型滿足完美混合（即網路是完全圖），則模型的動力方程為：

\[\begin{aligned} &\frac{d S}{d t}=-\beta S I \\ &\frac{d R}{d t}=\delta I \\ &\frac{d I}{d t}=\beta S I-\delta I \end{aligned} \]

處於\(S\)、\(I\)、\(R\)狀態的節點數量隨著時間變化曲線如下圖所示：
遷移學習和多工學習之間的區別

3.3 SIS模型

SIS模型中節點只有S-I兩個階段，它假設已經治癒的節點會立即變為易感節點。節點的狀態轉移圖如下：

這裡我們把\(s=\frac{\beta}{\delta}\)定義為病毒的「力量」（strength）。

該模型可用於對流感的建模，也即已被感染的節點經過治癒後會重新回到易感狀態。

同樣我們假設模型滿足完美混合（即網路是完全圖），則模型的動力方程為：

\[\begin{aligned} &\frac{d S}{d t}=-\beta S I+\delta I \\ &\frac{d I}{d t}=\beta S I-\delta I \end{aligned} \]

處於\(S\)、\(I\)狀態的節點數量隨著時間變化曲線如下圖所示：
遷移學習和多工學習之間的區別

3.4 傳染閾值

接下來我們考慮SIS模型中的傳染閾值(epidemic threshold)\(\tau\)。對於\(SIS\)模型而言，流行閾值可以是任意的。

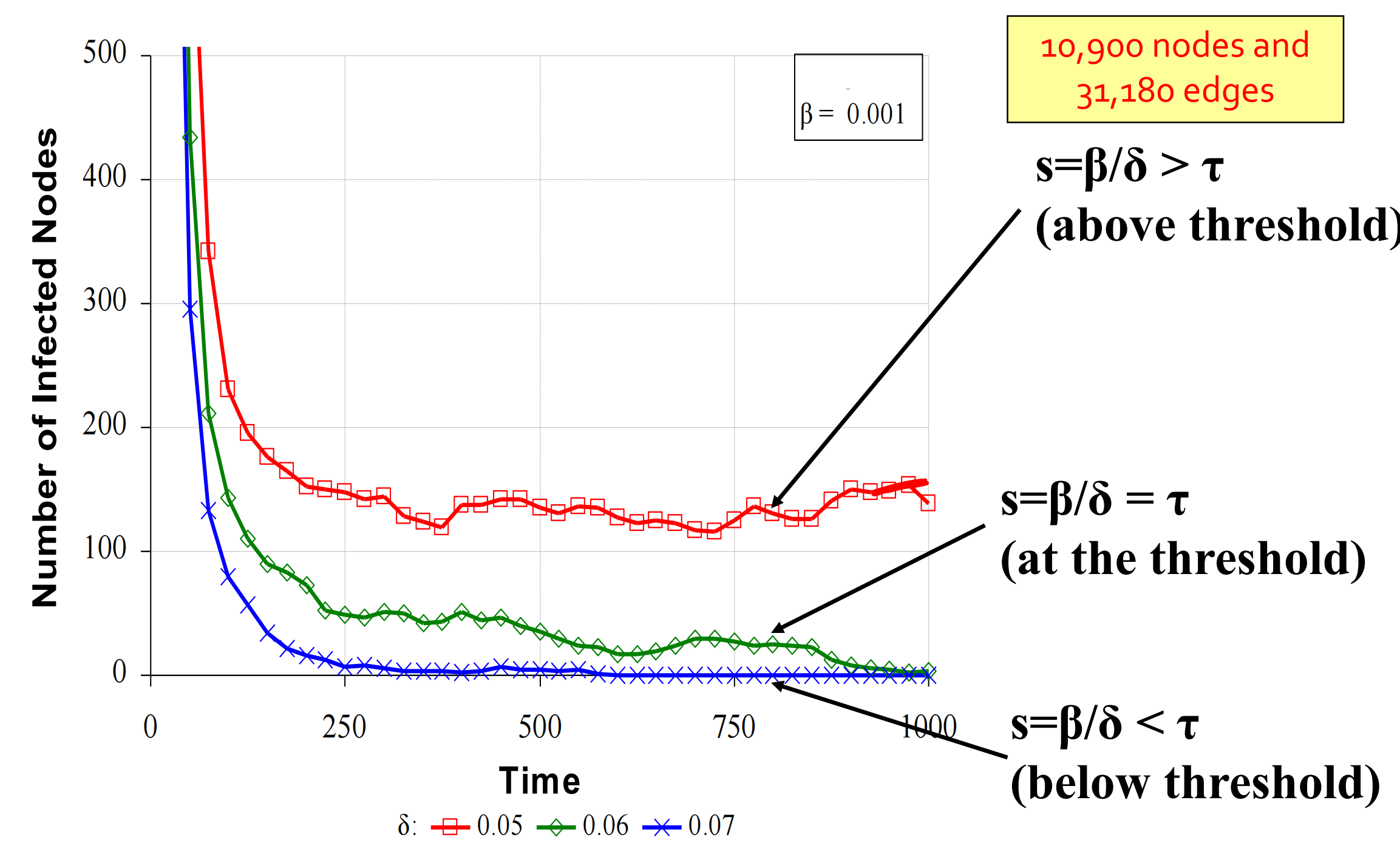
我們設圖\(G\)的傳染閾值為\(\tau\)。如果病毒的「力量」\(s=\frac{\beta}{\delta} < \tau\)（這裡\(\beta\)指病毒的死亡率，\(\delta\)指病毒的出生率），則疾病的流行就不會發生（它最終會消失）。事實上，圖\(G\)的傳染閾值\(\tau\)可以表示為

\[\tau=\frac{1}{\lambda_{1, A}} \]

這裡\(\lambda_{1, A}\)為圖\(G\)的鄰接矩陣最大的特徵值。這個定理看起來非常神奇，因為我們只用\(\lambda_{1,A}\)就捕捉到了整個圖的屬性！

以下是在AS圖上，當\(s\)大於、小於或等於傳染閾值\(\tau\)時的感染節點數量隨時間變化圖：

如果我們再考慮不同的初始感染人數，則會得到以下的感染人數變化影象：

3.5 一個埃博拉的例子

在一個埃博拉的例子^[1]中，設定如下的轉換狀態：
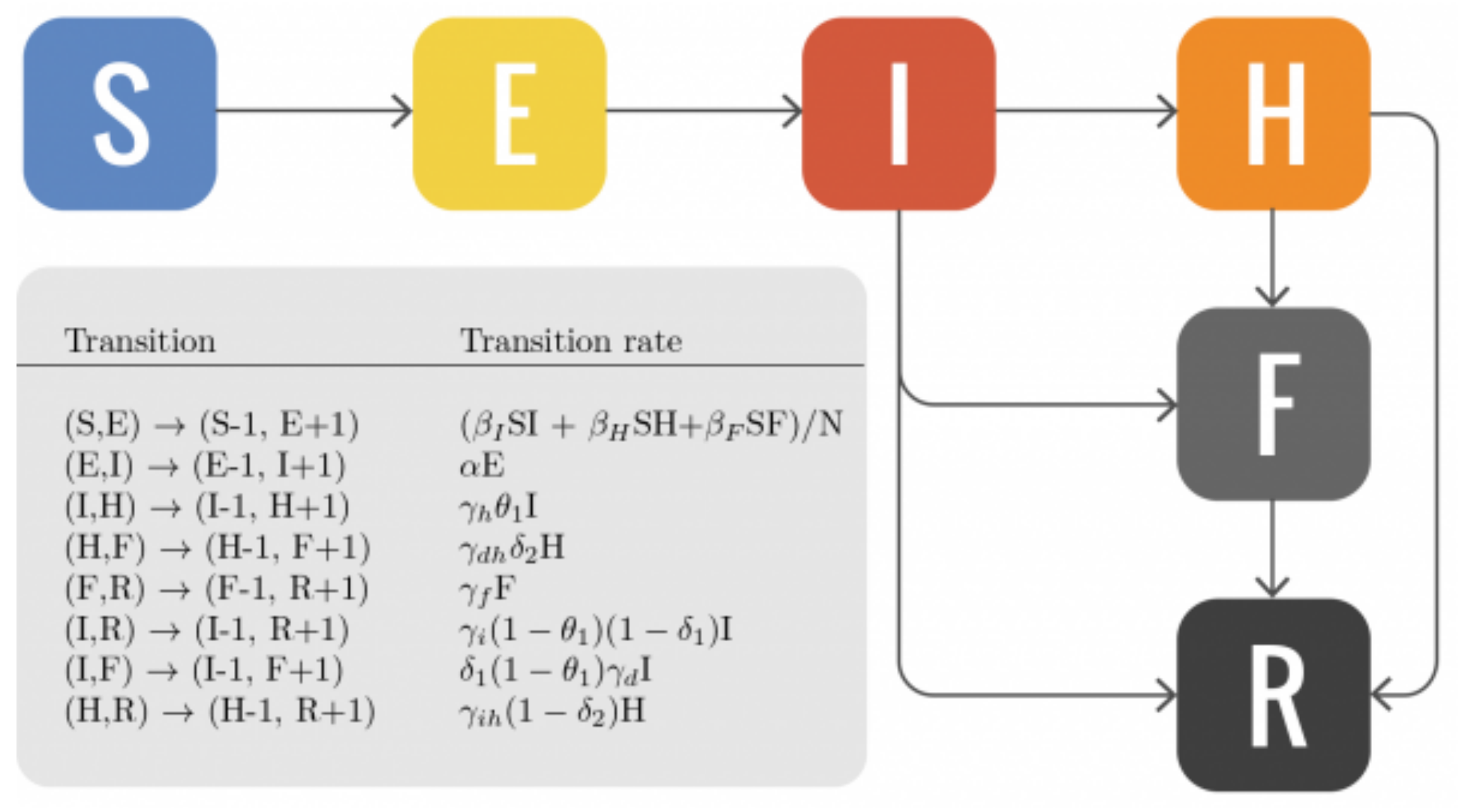
遷移學習和多工學習之間的區別

當設定\(R_0=1.5\text{-}2.0\)時，總死亡人數隨時間變化如下：

參考

[1] Gomes M F C, y Piontti A P, Rossi L, et al. Assessing the international spreading risk associated with the 2014 West African Ebola outbreak[J]. PLoS currents, 2014, 6.
[2] http://web.stanford.edu/class/cs224w/
[3] Easley D, Kleinberg J. Networks, crowds, and markets: Reasoning about a highly connected world[M]. Cambridge university press, 2010.
[4] Barabási A L. Network science[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 371(1987): 20120375.

圖資料探勘：基於概率的流行病模型