1 網路中的傳播

1.1 一些傳播的例子

我們現在來研究網路中的傳播。事實上，在網路中存在許多從節點到節點級聯的行為，就像傳染病一樣。這在不同領域中都有所體現，比如：

生物學 傳染性疾病
資訊科技 級聯故障，資訊的傳播
社會學 謠言、新聞、新技術的傳播，虛擬市場

下圖就展示了一個資訊經由媒體擴散（diffusion）的過程：

1.2 基於網路構建傳播模型

接下來我們看如何基於網路構建傳播模型。以傳染病為例，傳染病會沿著網路的邊進行傳播。這種傳播形成了一個傳播樹，也即級聯，如下圖所示：

我們定義一些術語：將其中傳播的物件為contagion；被傳染這一事件稱為adoption、infection或activation；已被傳染的節點稱為infected/active nodes或adoptors。

接下來我們來看如何為擴散進行建模。目前已經提出了決策模型和概率模型兩種模型。

決策模型 在這種模型中每個節點會先觀察其鄰居的決策，然後再以此為依據做出自己的決策。比如若我的\(k\)個朋友去參加了遊行，那麼我就去。
概率模型 在這種模型中一個已被傳染的節點會以一定概率傳染其它沒有被傳染的節點。比如我有幾個鄰居已經被傳染，那麼我也有一定概率被傳染。這種模型通常用於影響或疾病傳播建模。

本篇文章我們介紹決策模型中的集體行動模型和協調博弈模型，下篇文章我們再介紹概率模型。

2 集體行動模型

2.1 模型介紹

Granvetter於1978年提出了集體行動（collective action）模型^[1]。在這種模型中，每個人都可以看見任何人的行為並以此為依據進行行動（這也就意味著我們假設網路是完全圖）。該模型在日常生活中的一些常見例子包括：在劇院鼓掌或起身離開、在股市中是否存錢以及日常生活中的抗議、罷工等等。接下來我們來探究參與某個給定活動的人數是如何隨著時間的推移而增減的。

設有\(n\)個人且每個人可以觀測到彼此的行動。對每個人\(i\)都有一個閾值\(t_i(0\leq t_i \leq 1)\)。當且僅當至少有佔比\(t_i\)的人採取了某個行為時，節點\(i\)也會採取該行為。事實上\(i\)節點採取行動的概率是如下的階躍函數（橫軸是採取行動的人數比例）：

遷移學習和多工學習之間的區別

小的\(t_i\)也就意味著\(i\)是一個早採納者（early adopter），而大的\(t_1\)則意味著\(i\)是一個遲採納者（late adopter）。我們假設這裡的時間步是離散的。

我們設\(\{t_1,\cdots, t_n\}\)為所有人的行動閾值集合。設\(F(x)\)為閾值\(t_i\leq x\)的人數比例（\(F(\cdot)\)事先已給定，它是傳染一個的屬性），它是非遞減的，即滿足：

\[F(x+\varepsilon) \geq F(x) \]

該模型是一個動態的模型，採取行動的人數會一步步地變化，如下圖所示：

圖中\(F(x)\)表示閾值\(t_i\leq x\)的人數比例，\(s(t)\)表示在\(t\)時刻已加入行動的人數比例。我們發現行動人數的變化速率並不均勻：中間最陡，說明大多數人的閾值比較集中，而左右兩端則可分別視為早採納者和晚採納者的閾值。

我們模擬\(s(t)\)隨著\(t\)的迭代過程：

\[\begin{aligned} &s(0)=0 \\ &s(1)=F(0) \\ &s(2)=F(s(1))=F(F(0)) \end{aligned} \]

我們進一步地進行模擬，有：

\[s(t+1)=F(s(t))=F^{t+1}(0) \]

直觀地理解該迭代，就是\(t\)時刻已加入的行動人數\(s(t)\)會在\(t+1\)時刻帶動更多的人（\(F(s(t))\)）加入行動。最終模型會收斂到不動點(fixed point)\(F(x)=x\)，如下圖所示：

當然，可能也存在其它不動點。不過從\(0\)開始我們只能到達其中的第一個。

如果我們想要從某個其它的地方開始這個過程，則可以往上/往下移動到下一個不動點：

如下圖所示，不動點有穩定不動點和不穩定不動點之分。穩定不動點周圍坡度較為平緩，不穩定不動點周圍坡度較為陡峭。

2.2 不連續的過渡

我們假設每個節點的閾值\(t_1\)是獨立地從分佈\(F(x)=\operatorname{Pr}[\text { thresh } \leq x]\)中取樣得到的。假定該分佈為\(\mu=45\)的截斷(truncated)正態分佈，則\(F(x)\)的影象會根據該分佈的方差進行變化，如下圖所示：

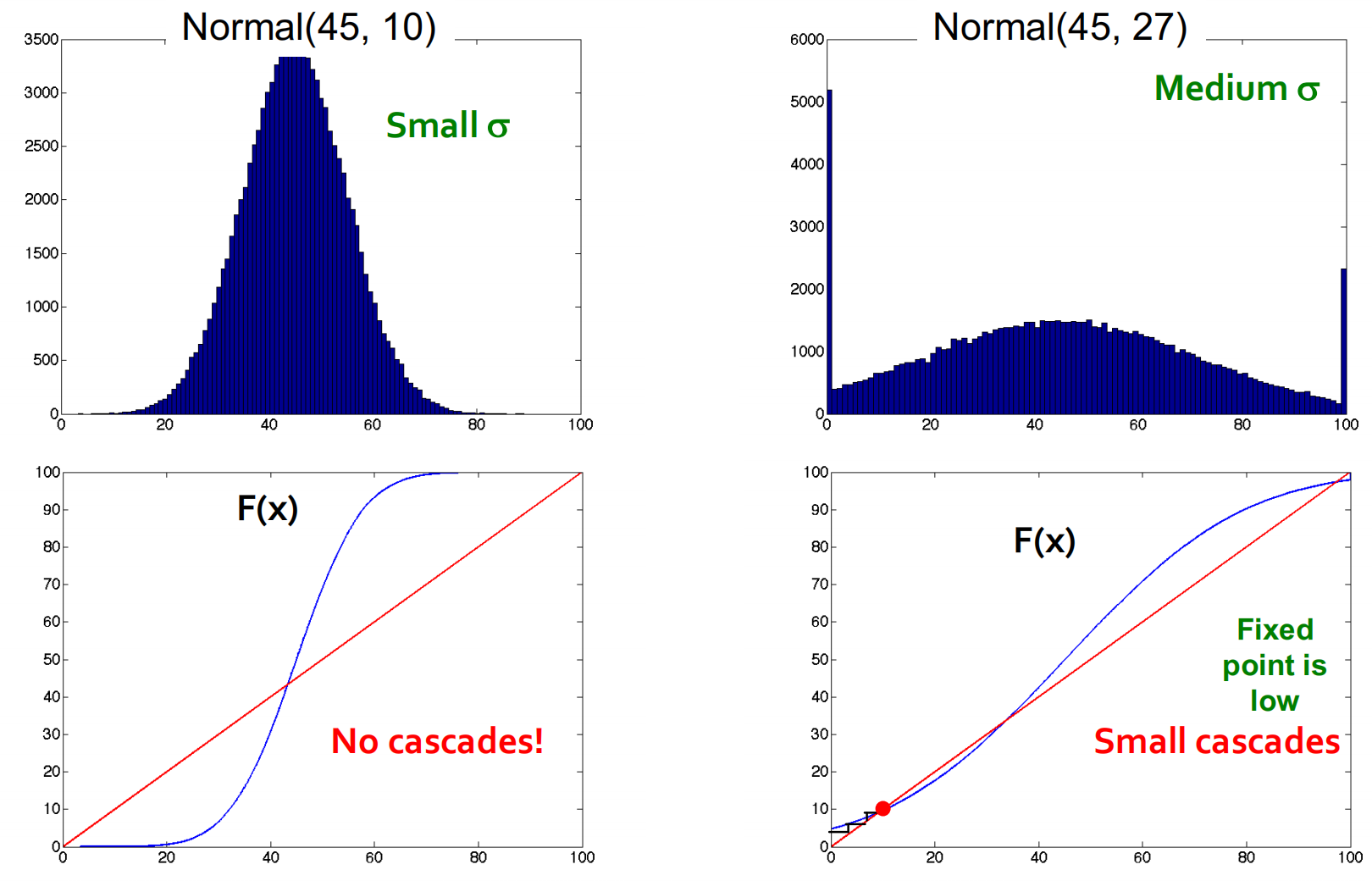
可以看見，大的方差會使早採納者和主流人群之間的過渡更為平穩。

我們嘗試再增大方差則不動點會升高，然而如果我們再進一步增大方差則不動點又會降低：

2.3 模型的弱點

首先，該網路缺少一些社群網路中的概念。比如在社群網路中有一些人是易受影響的。而這直接關係到誰是早採納者，而不僅僅是早採納者有多少。

此外，該模型僅僅是建模了人們對參與人數的認識，而不是實際參與人數的多少。也即和「你認為誰會採取該行為」和「誰實際採取了該行為」的區別。這會導致人們在一段時間被「鎖定」在某些選擇上。

最後，在對閾值的建模上，我們還可以探索更多的分佈，或者從一些基礎理論（如博弈論模型）來對閾值進行推導。

2.4 多元無知現象

上述的模型需要假設網路是完全圖的。然而在現實世界，每個人接受的資訊其實大都是片面的，而這會導致他們根據周圍的資訊來對集體行動做出的決定並不靠譜。比如若某個專制政府限定公民之間的溝通，那麼就算已經有足夠大的人口比例想反對當前政府並採取極端措施，他們也會覺得自己是一個小群體，並認為這種反抗有很大風險。

多元無知(pluralistic ignorance) 是指人們普遍地錯誤估計整個民眾對一些意見的反應。這是一個使用廣泛的原則，不僅僅是在一箇中央集權制度限制資訊的流通環境。例如，1970年在美國進行的一項調查表明（同一時期實施的幾個調查也得到了類似的結果），雖然那個時期只有少數美國白人主張種族隔離，大大超過\(50\%\)的人認為他們所在地區大多數美國白人支援這個主張^[2]。

3 協調博弈模型

3.1 模型介紹

該模型基於兩個玩家的協調博弈（coordination game）理論，假設每人只能從行為\(A\)或\(B\)中選一個來採納，且如果你和你的朋友採取了相同的行為，則你會獲得回報（payoff）。

我們定義一個如下圖所示的關於節點\(v\)和\(w\)的回報矩陣，使得當\(v\)和\(w\)都採取行為\(A\)的時候，它們獲得回報\(a>0\)；當\(v\)和\(w\)都採取行為\(B\)的時候，它們獲得回報\(b>0\)；當\(v\)和\(w\)採取相反行為的時候，它們獲得\(0\)回報。

	w-A	w-B
v-A	\(a,a\)	\(0,0\)
v-B	\(0,0\)	\(b,b\)

每個節點\(v\)和會和所有其鄰居進行一次這個遊戲，最終算將每次進行遊戲的回報進行求和。

接下來我們來看節點\(v\)如何做出決策。

我們設節點\(v\)擁有\(d\)個鄰居，\(p\)為其鄰居中採取行動\(A\)所佔的數量，\((1-p)d\)為其鄰居中採取行動\(B\)所佔的數量。則\(v\)採取行動\(A\)和\(B\)分別獲得的總回報分別為：

\[\begin{aligned} \text { Payoff }_v &=a \cdot p \cdot d & & \text { if } v \text { chooses } A \\ &=b \cdot(1-p) \cdot d & & \text { if } v \text { chooses B } \end{aligned} \]

當\(a \cdot p \cdot d>b \cdot(1-p) \cdot d\)時\(v\)會採取行為\(A\)。進一步化簡得到

\[p>\frac{b}{a+b} \]

我們設\(q=\frac{b}{a+b}\)為回報閾值，即當\(p>q\)時\(v\)會選擇行為\(A\)。

3.2 傳播範例

接下來我們來看一個協調博弈模型的傳播範例。給定一個圖，我們設每個人最開始都採取的行為\(B\)。設存在一個由行為\(A\)的早採納者所組成的小子集\(S\)，且我們假定他們是頑固派(Hard-wire)，也即他們始終會採取行為\(A\)而不管使用多少回報來企圖改變他們。

我們假定有以下的回報設定：對於一個節點而言，如果他的朋友中有大於\(q=50\%\)的人採取行為\(A\)，則他也採取行為\(A\)。這也就意味著\(a=b-\epsilon\)(\(\epsilon>0\)是一個小的正常數)且\(q=\frac{1}{2}\)。

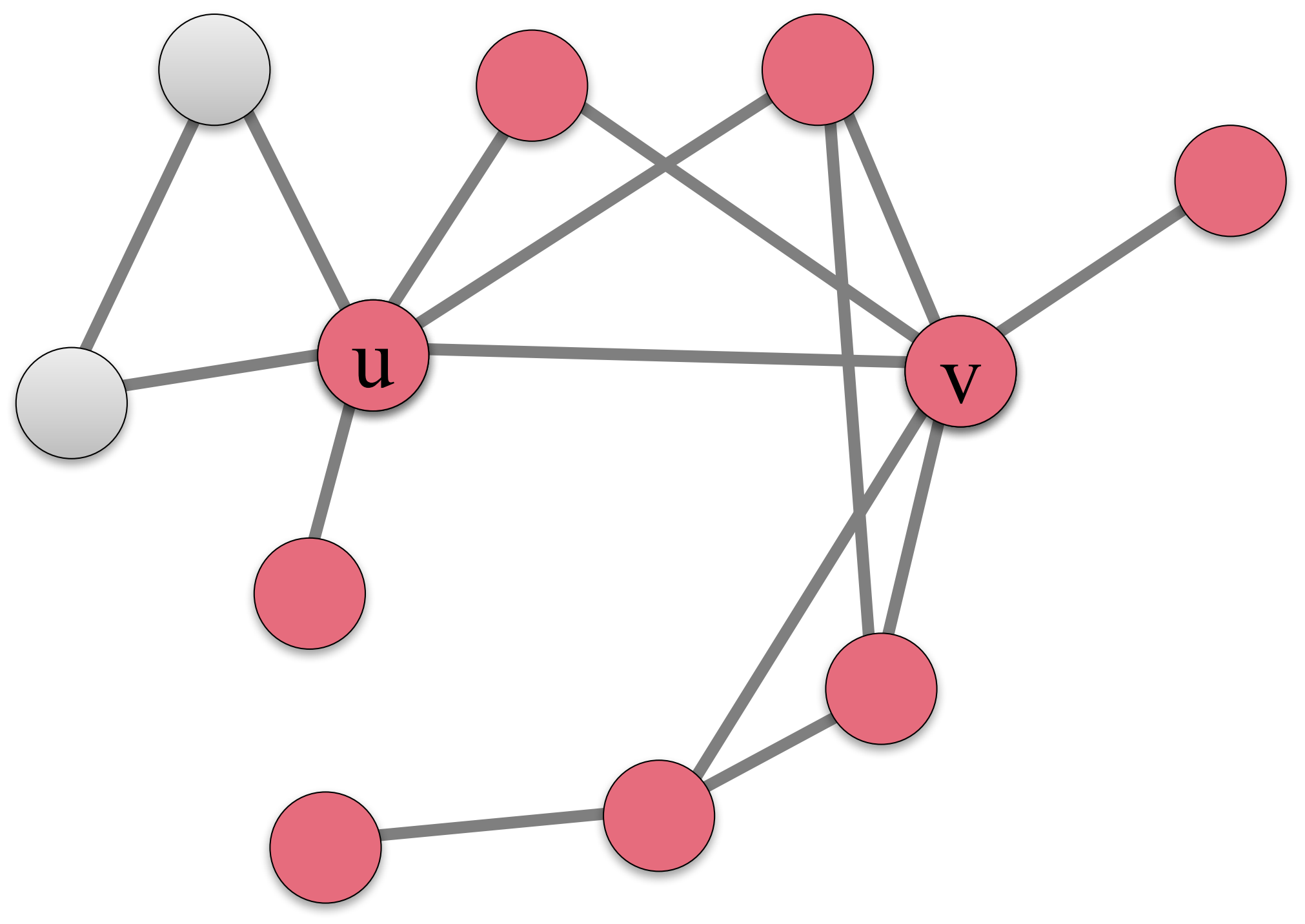
我們接下來看傳播的模擬情況。初始時，\(S=\{u,v\}\)，它們採取行為\(A\)，被標記為紅色。

如果我的朋友超過\(q=50\%\)是紅色，則我也為紅色。於是下一步該網路變化為：

又過了一個時間步變為：

最後，網路變化為：

參考

[1] Granovetter M. Threshold models of collective behavior[J]. American journal of sociology, 1978, 83(6): 1420-1443.
[2] O'Gorman H J, Garry S L. Pluralistic ignorance—A replication and extension[J]. Public Opinion Quarterly, 1976, 40(4): 449-458.
[3] http://web.stanford.edu/class/cs224w/
[4] Easley D, Kleinberg J. Networks, crowds, and markets: Reasoning about a highly connected world[M]. Cambridge university press, 2010.
[5] Barabási A L. Network science[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 371(1987): 20120375.

圖資料探勘：網路中的級聯行為