1 六度分隔理論

先來看兩個有趣的例子。我們建立一個好萊塢演員的網路，如果兩個演員在電影中合作或就將他們連結起來。我們定義一個演員的貝肯數（bacon number）是他們與演員凱文·貝肯有多少步的距離，貝肯數越高，演員離凱文·貝肯越遠。研究發現，直到2007年12月，最高（有限）的貝肯數僅為\(8\)，且大約只有12%的演員沒有路徑連結到凱文·貝肯。

此外，在學術合作中，埃爾德什數(Erdős number)被用來描述數學論文中一個作者與Pual Erdős的「合作距離」(Pual Erdős就是我們在部落格《圖資料探勘：Erdos-Renyi隨機圖的生成方式及其特性》中提到的那位巨佬)。菲爾茨獎獲得者的埃爾德什數中位數最低時為3，CS224W講師Jure Leskovec（也是一點陣圖資料探勘大佬）的埃爾德什數為3.

看完這兩個例子我們不禁會思考，兩個人之間的典型最短路徑長度是多少呢？事實上，哈佛大學心理學教授斯坦利·米爾格拉（Stanley Milgram）早在1967年就做過一次連鎖實驗^[1]，他將一些信件交給自願的參加者，要求他們通過自己的熟人將信傳到信封上指明的收信人手裡。他發現，296封信件中有64封最終送到了目標人物手中。而在成功傳遞的信件中，平均只需要5次轉發，就能夠到達目標。也就是說，在社會網路中，任意兩個人之間的「距離」是6。這就是所謂的六度分隔理論，也稱小世界現象。儘管他的實驗有不少缺陷，但這個現象引起了學界的注意。

2 小世界網路模型

六度分隔理論令人吃驚的地方其實還不在於其任意兩個人之間的路徑可以如此之短，而是在保證路徑如此之短的情況下還保證了高的聚集性。

短路徑從直覺上可以理解，因為每個人認識了超過\(100\)個能直呼其名的朋友，而你的每個朋友除你之外也至少有\(100\)個朋友，原則上只有兩步之遙你就可以接近超過\(100\times 100=10000\)個人。然而問題在於，社會網路呈三角形態，即三個人相互認識，也就是說你的\(100\)個朋友中，許多人也都相互認識。因此，當考慮沿著朋友關係構成的邊到達的節點時，很多情況是從一個朋友到另一個朋友，而不是到其它節點。前面的數位\(10000\)是假設你的\(100\)個朋友連線到\(100\)個新朋友，如果不是這樣則經過兩步你能達到的朋友數將大大減小。

由此看來，小世界現象從區域性角度看社會網路的個體被高度聚集，卻還能保證任意兩個人之間的路徑如此之短，確實令人吃驚。

2.1 權衡聚類係數和圖的直徑

正如我們前面所說，聚類係數與圖任意兩點間的最短路徑（可以通過圖的直徑來體現）有著矛盾的關係。比如在下面所示的這個網路雖然直徑小，但聚類係數低：

而下圖這個具有「區域性」結構的網路聚類係數雖高（即滿足三元閉包，我朋友的朋友也是我朋友），但其網路直徑大：

我們是否可以同時擁有高的聚類係數與小的直徑呢？直覺上，我們發現聚集性體現著邊的區域性性（locality），而隨機產生的邊會產生一些捷徑（shortcuts），如下圖所示：

這樣，我們在保持邊聚集性的條件下，隨機地新增一些邊，那麼就能夠完成要求了。根據這個思想，人們提出了許多小世界模型，我們接下來介紹Watts-Strogatz模型。

2.2 Watts-Strogatz模型

Watts-Strogatz提出的小世界模型^[2]包含兩個部分：

(1) 低維的正則網格(lattice)
首先需要一個低維的正則網格模型來滿足高的聚類係數。在下面的例子中我們使用一維的環狀網路(ring)作為網格。

(2) 重新排布邊(rewire)
接著在網格的基礎上新增/移除隨機邊來創造捷徑，以連線網格的遠端部分。每條邊有概率為\(p\)被隨機地重新排布（將其一端點連線到一個隨機節點）。

如下就是一個小世界網路的例子：

邊的重新排布允許我們在正則網格和隨機圖之間形成一種「插值」：

如下圖所示，我們直觀地發現如果想破壞聚類結構需要大量的隨機性注入（即邊隨機重排的概率大），然而只需要少量的隨機性注入就可以產生捷徑。

接下來我們來根據一個範例分析其聚類係數和直徑。我們基礎網格模型選用方格，每個節點有一個隨機產生的長距離邊(long-range edge)，如下圖所示：

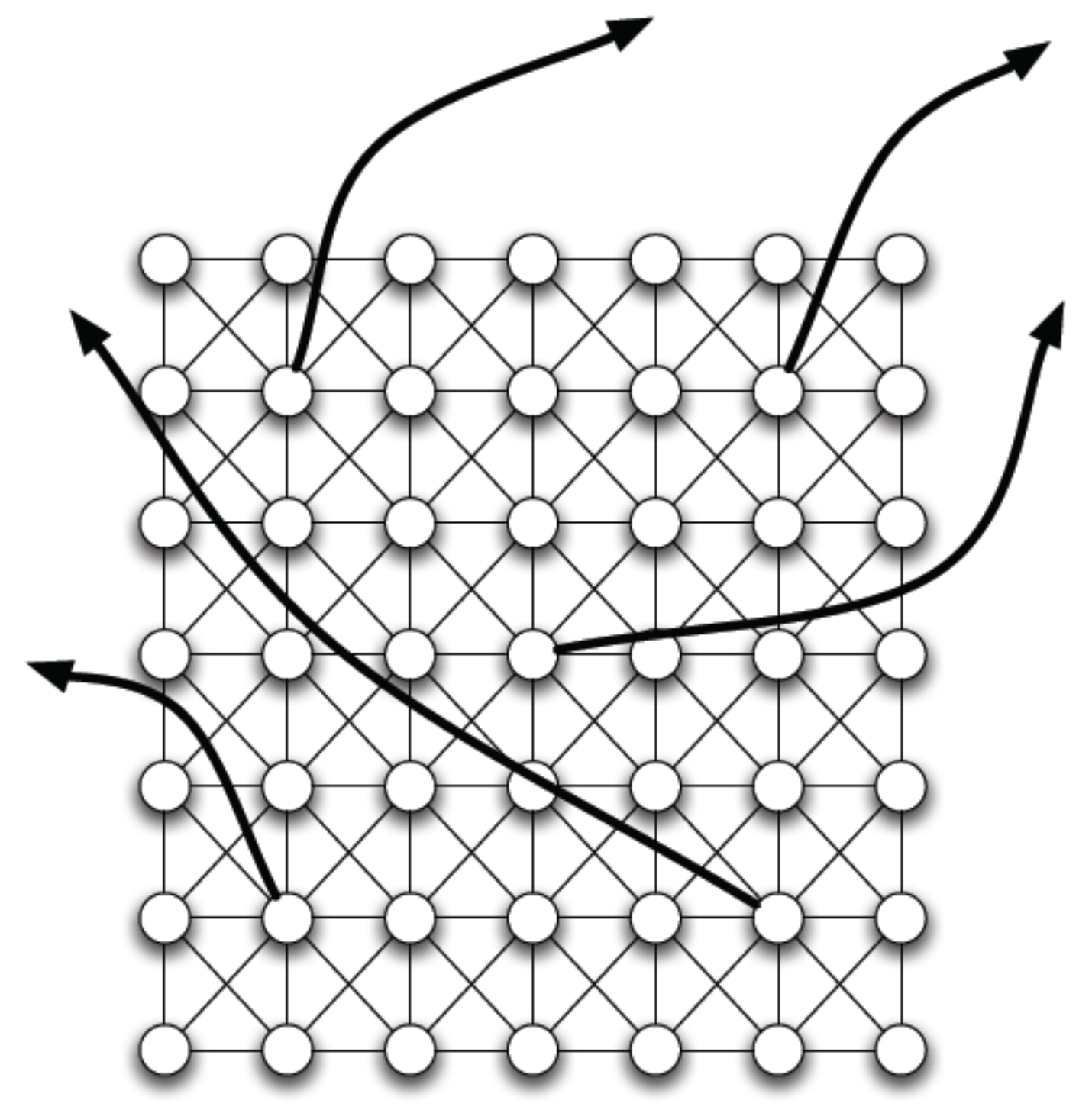
對於正中央的那個節點，我們有其聚類係數

\[C_i=\frac{2 \cdot e_i}{k_i\left(k_i-1\right)}=\frac{2 \cdot 12}{9 \cdot 8} \geq 0.33 \]

我們接下來來證明其直徑是\(O(\log n)\)的。

我們將每個\(2\times2\)都子圖合併為一個超節點，以形成一個超圖，如下圖所示：
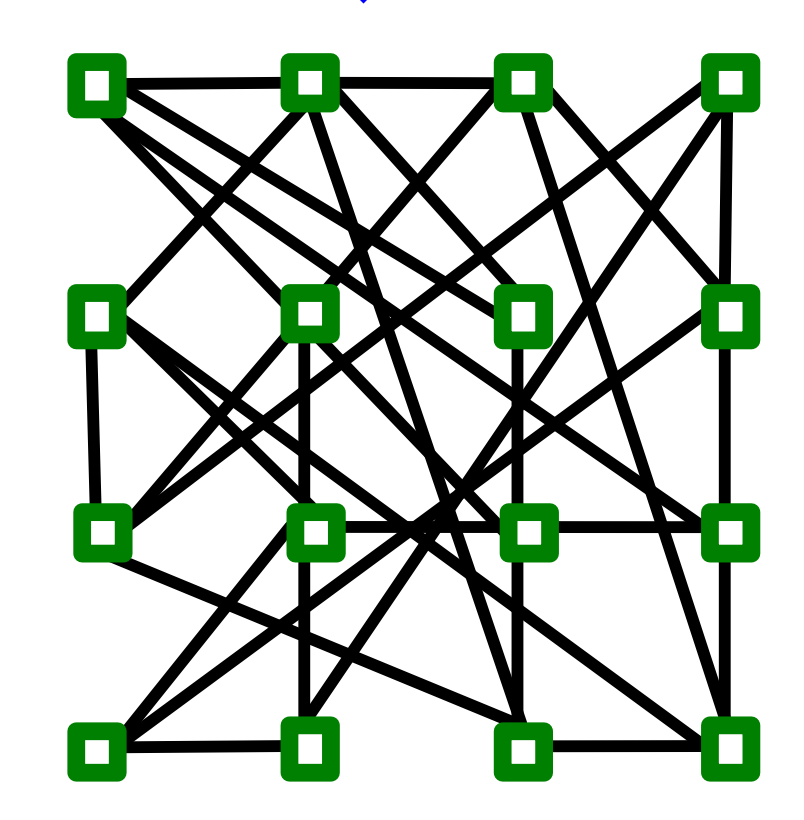
遷移學習和多工學習之間的區別

每個超節點有4條邊伸出去，這是一個4-正則隨機圖。我們在每條長距離邊上新增最多兩步（必須遍歷內部節點）將每個超節點之間的最短路徑轉變為真實圖中的路徑。
於是我們得到該模型的直徑為\(O(2\log n)\)

3 分散式搜尋

接下來我們考慮另外一個問題：即如何找到到指定目標節點的最短路徑，即對網路進行導航(navigation)。

3.1 問題定義

我們設開始節點為\(s\)，目標節點為\(t\)。訊息要從節點\(s\)開始，沿著網路中的邊最終被傳遞到目標節點\(t\)。的起初節點\(s\)只知道其朋友的位置和目標的位置，且除了自己的連結之外，並不知道其它節點的連結情況。路徑上每個中間節點也都僅具有這種區域性資訊，而且它們必須選擇某個鄰居轉發該訊息。這些選擇相當於尋找一條從\(s\)到\(t\)的路徑。我們將搜尋時間（search time）\(T\)定義為訊息從\(s\)轉發到\(t\)所需要的步數。

3.2 Watts-Stogatz模型中的搜尋

Watts-Stogatz模型即我們前面提到的，每個節點都有一條隨機邊的二維網格：

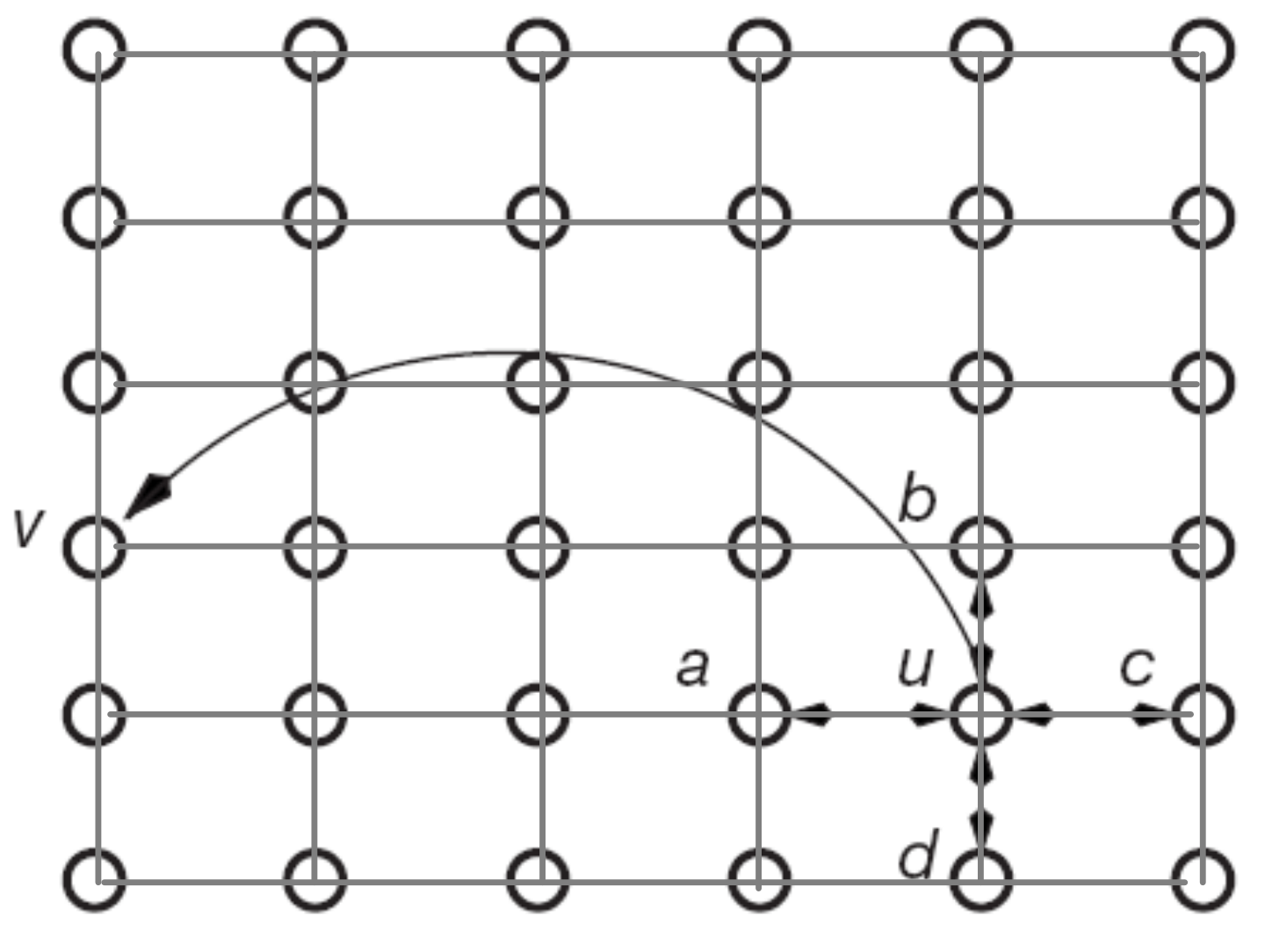
由於是小世界網路，其直徑為\(O(\log n)\)。

然而令人遺憾的是，儘管存在長度僅為\(O(\log n)\)步的路徑，但Watts-Stogatz模型中的去中心化搜尋演演算法在期望上需要\(n^{2/3}\)步來到達目標節點\(t\)，這也就意味著Watts-Stogatz模型是不可搜尋的（is not searchable）。

證明

我們先來證明一維的情況。我們想要證明Watts-Stogatz是不可搜尋的，則需要為其搜尋時間證明一個下界(lower bound)。

我們設定\(n\)個節點在一個環狀網路(ring)上，且每個節點都有一個有向隨機邊。如下圖所示：

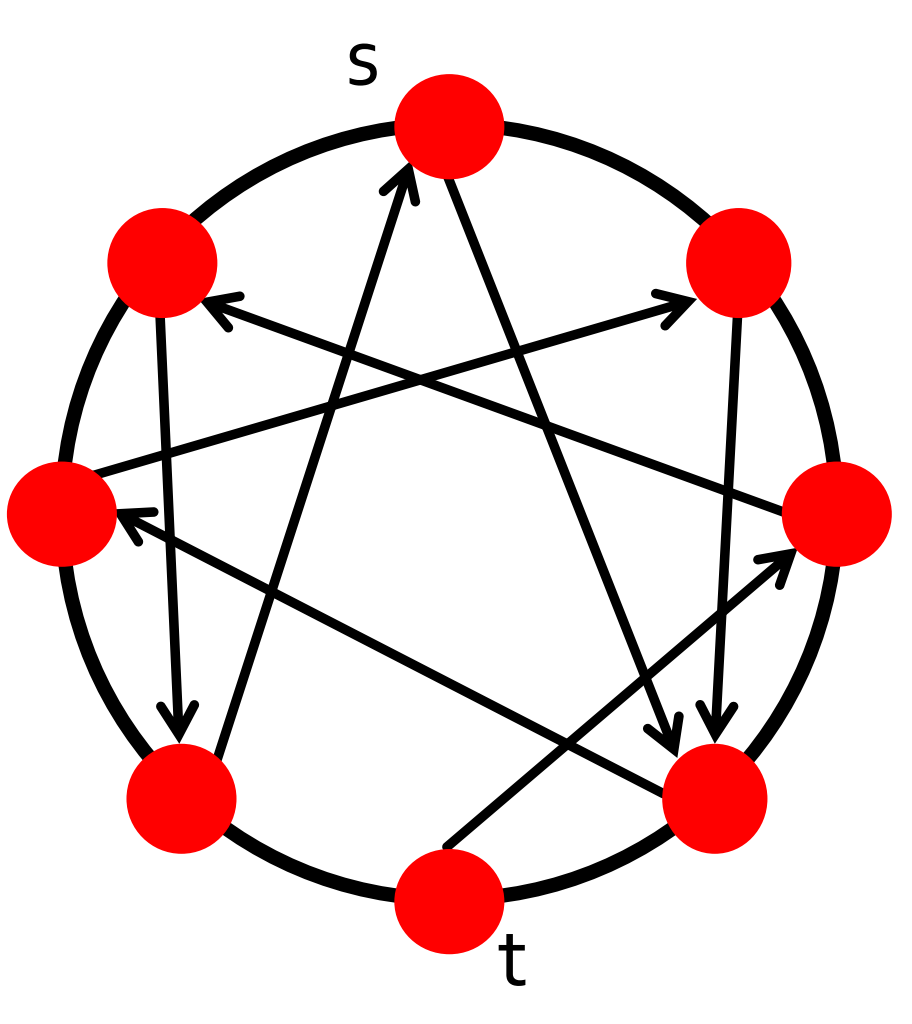
我們接下來會證明對環狀網路（一維網格），搜尋時間\(T \geq O(\sqrt{n})\)。

我們採用的證明策略為延期決定原則（principle of defered decision），即我們假設僅在到達某個節點後才碰到隨機長距離連結。

我們設\(E_i\)是一個隨機事件，表示從節點\(i\)發出的長距離連結指向某個在\(t\)周圍間隔\(I\)中的節點（間隔寬度為\(2\cdot x\)個節點），如下圖所示：

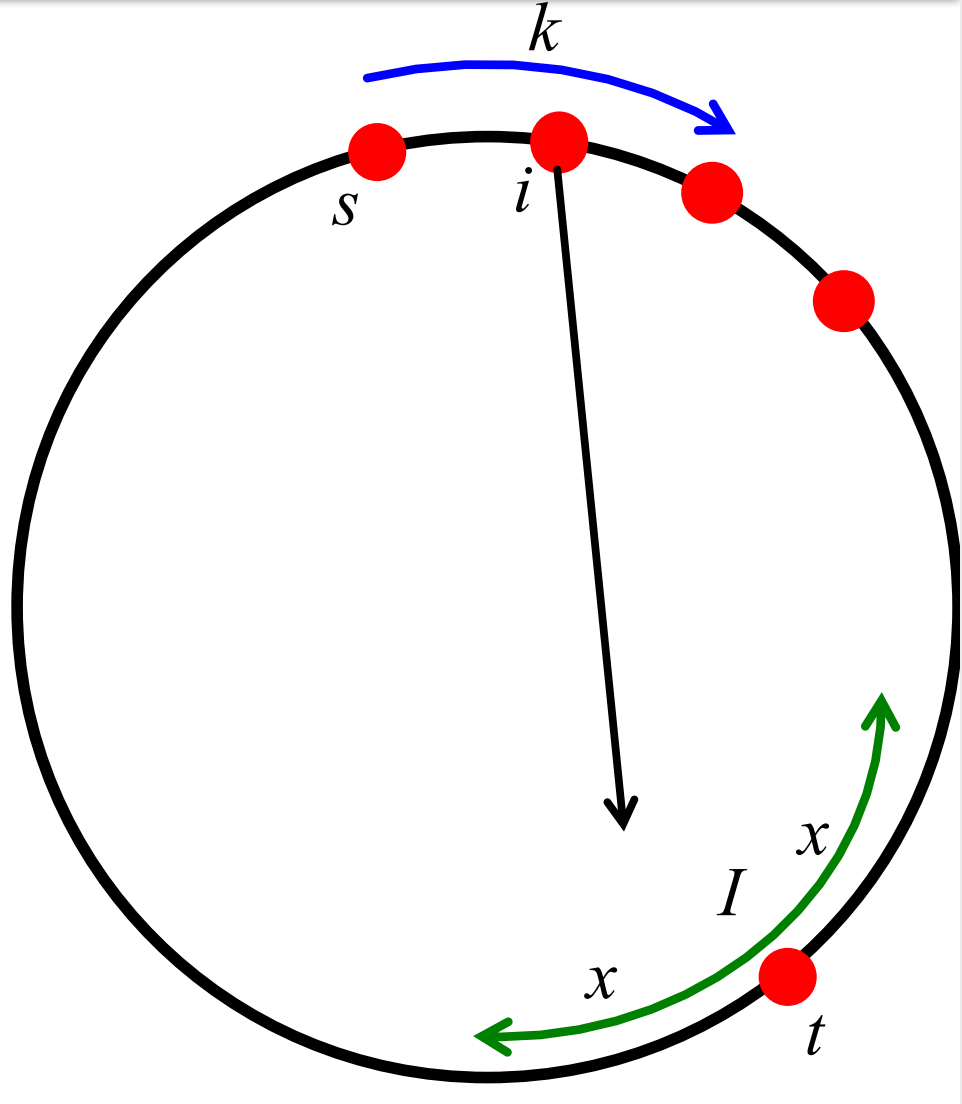
接著我們有

\[P\left(E_i\right)=\frac{2 x}{n-1} \approx \frac{2 x}{n}(在n很大的條件下) \]

設隨機事件\(E\)為演演算法存取的前\(k\)個節點中，有一個擁有到\(I\)的連結（任意一個節點都行），如下圖所示：

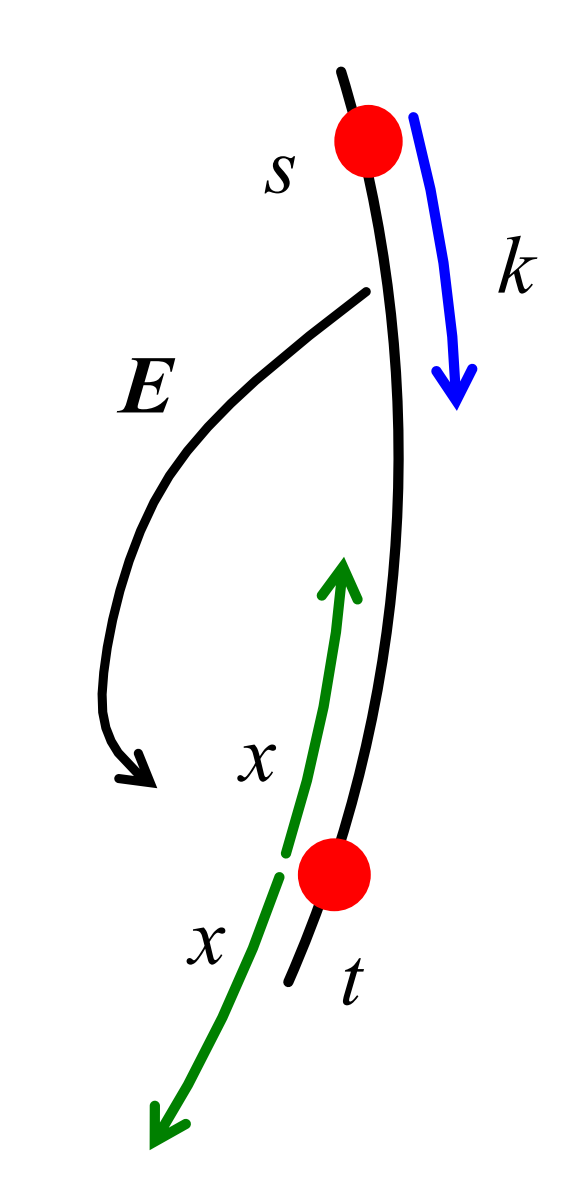
則

\[P(E)=P\left(\bigcup_i^k E_i\right) \leq \sum_i^k P\left(E_i\right)=k \frac{2 x}{n} \]

我們選擇\(k=x=\frac{1}{2} \sqrt{n}\)，則：

\[P(E) \leq 2 \frac{\left(\frac{1}{2} \sqrt{n}\right)^2}{n}=\frac{1}{2} \]

這實際上也就意味著在\(\frac{1}{2}\sqrt{n}\)步可以跳到\(t\)周圍\(\frac{1}{2}\sqrt{n}\)步內的概率\(\leq \frac{1}{2}\)。

假設初始點\(s\)在\(I\)之外，且事件\(E\)沒有發生(最先存取的\(k\)個節點都沒有連結指向\(I\))，則搜尋演演算法必須要花費\(T \geq \min (k, x)\)步來到達\(t\)。這兩個下界分別對應以下兩種情況：
Case 1 恰好在我們存取\(k\)個節點後，就碰到了一個很好的遠端連結，此時共花費\(k\)步。
Case 2 \(x\)和\(k\)重疊了，由於\(E\)沒有發生，我們必須至少要走\(x\)步。

這兩種情況分別如下圖所示：

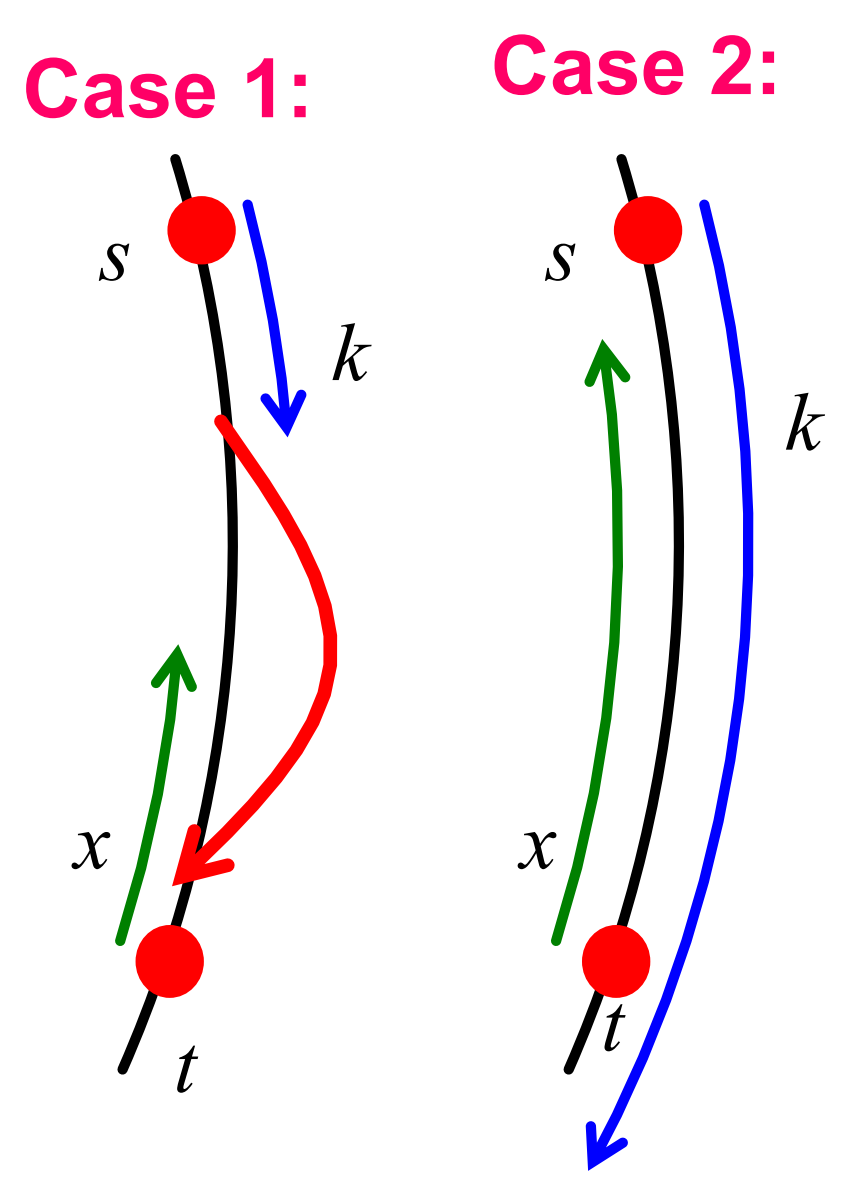
再加上根據前文的推論，我們有

\[T\geq P(E) (\# \text { steps })+P(\text { not } E) \min \{x, k\} \]

而我們前面已經說明了當\(x=k=\frac{1}{2} \sqrt{n}\)時，\(E\)有\(\frac{1}{2}\)的概率不發生。如果\(E\)不發生，則我們必須再走\(\geq \frac{1}{2} \sqrt{n}\)的步數才能到達\(t\)，如下圖所示：

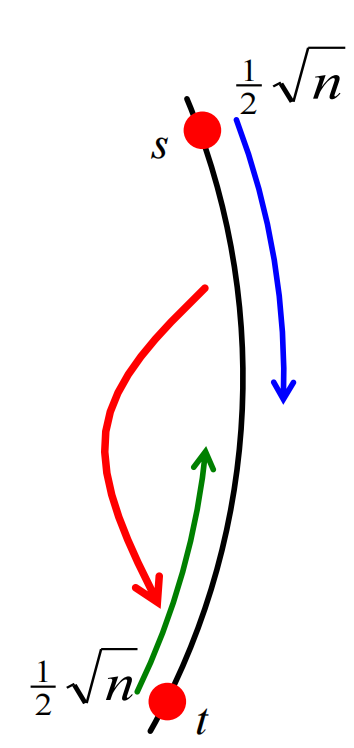
則到達\(t\)的期望時間

\[T \geq P(\text{not} E) \cdot \min \{x, k\}=\frac{1}{2} \frac{1}{2} \sqrt{n}=\frac{1}{4} \sqrt{n} \]

得證。

同理我們可以證明對\(d\)維網格，有\(T \geq O\left(n^{d /(d+1)}\right)\)。

既然Watts-Stogatz模型是不可搜尋的，我們如何構建一個可搜尋的小世界圖呢？接下來我們來介紹Watts-Stogatz模型的擴充套件版——Kleinberg模型。該模型同時具備我們所需要的兩種性質：網路包含短路徑，且通過分散搜尋在可接受時間內發現這些短路徑。

3.3 Kleinberg模型中的搜尋

Kleinberg模型^[3]基於以下直覺：長距離連結(long range links)並不是隨機的，它們是根據節點的地理位置分佈來的，因此我們可以使每個節點之間的隨機邊以距離衰減的方式生成。

八卦：Kleinberg也是個大牛，在ICM上做了題為「 Complex networks and decentralized search algorithms」的45分鐘報告。

該模型仍然是基於網格的，且每個節點有一個長距離連結，不過該模型創新性地定義了節點\(u\)長距離連結到\(v\)的概率為：

\[\mathrm{P}(\mathrm{u} \rightarrow \mathrm{v})=\frac{\mathrm{d}(\mathrm{u}, \mathrm{v})^{-\alpha}}{\sum_{w \neq u} \mathrm{~d}(\mathrm{u}, \mathrm{w})^{-\alpha}} \]

這裡\(d(u,v)\)指\(u\)和\(v\)之間的網格距離（即一個節點沿著到相鄰節點的邊到另一節點的步數），\(\alpha\geqslant0\)。分母\(\sum_{w \neq u} \mathrm{~d}(\mathrm{u}, \mathrm{w})^{-\alpha}\)實際上是一個和\(d\)無關的歸一化常數（後面我們會詳細討論），用於表示\(u\)到所有其它節點的距離和，因此我們實際上有：

\[\mathrm{P}(\mathrm{u} \rightarrow \mathrm{v}) \sim \mathrm{d}(\mathrm{u}, \mathrm{v})^{-\alpha} \]

在不同\(\alpha\)的設定下，\(\text{P}(u\rightarrow v)\)隨著\(d\)變化示意圖如下：

當\(\alpha=0\)時，\(P(u\rightarrow v)\)服從均勻分佈，即節點之間的邊完全隨機產生，此時Kleinberg模型退化到Watts-Stogatz模型。

接下來我們介紹如何在Kleinberg模型中做搜尋。我們接下來會證明在一維情況下，當\(\alpha=1\)時，從\(s\)到\(t\)的期望步數為\(O\left(\log (n)^2\right)\)。

我們假設某個節點\(v\)滿足\(d(v,t)=d\)，並設定間隔\(I=d\)：

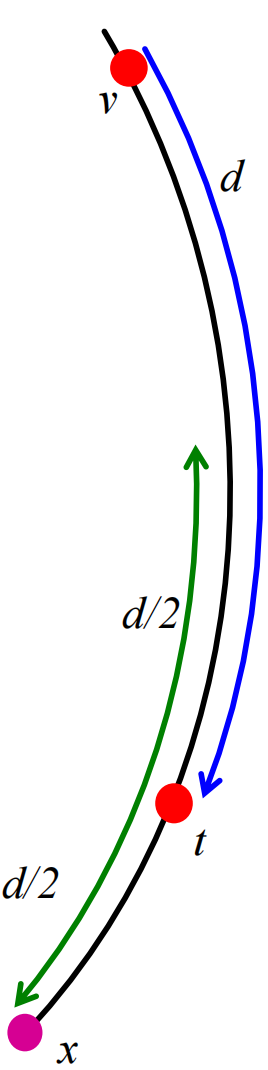
則我們可以證明從\(v\)到\(I\)中的某節點存在長距離連結的概率滿足

\[P\left(\begin{array}{l} \text { Long range } \\ \text { link from } v \\ \text { points to a } \\ \text { node in } I \end{array}\right)=O\left(\frac{1}{\ln n}\right) \]

這個定理非常酷，這是因為當\(d\)增大時，\(I\)會變得寬，但是該概率卻和\(d\)是獨立的。

下面我們來看該定理的證明。

首先我們有

\[\mathrm{P}(\mathrm{v} \rightarrow \mathrm{w})=\frac{\mathrm{d}(\mathrm{v}, \mathrm{w})^{-1}}{\sum_{u \neq v} \mathrm{~d}(\mathrm{v}, \mathrm{u})^{-1}} \]

這裡\(w\)為區間\(I\)中的一個點，歸一化常數

\[\sum_{u \neq v} d(v, w)^{-1}=\sum_{\substack{\text { all possible } \\ \text { distancess }d\\\text{from } 1 \rightarrow n/2}} 2 \frac{1}{d}=2 \sum_{d=1}^{n / 2} \frac{1}{d} \leq 2 \ln n \]

這裡第一個等式成立是因為每個可能的距離\(d\)都對應兩個節點，而從每個點產生連結的概率都為\(\frac{1}{d}\)。最後一個不等式成立是因為\(\sum_{d=1}^{n / 2} \frac{1}{d} \leq 1+\int_1^{n / 2} \frac{d x}{x}=1+\ln \left(\frac{n}{2}\right)=\ln n\)，即用\(y=\frac{1}{x}\) 下方的面積來確定調和級數的上界，如下圖所示：

因此，我們從有\(v\)連結到間隔\(I\)的概率

\[\begin{aligned} P(v \text { points to } I)&=\sum_{w \in I} \mathrm{P}(\mathrm{v} \rightarrow \mathrm{w}) \geq \sum_{w \in I} \frac{\mathrm{d}(\mathrm{v}, \mathrm{w})^{-1}}{2 \ln n}\\ &=\frac{1}{2 \ln n} \sum_{w \in I} \frac{1}{d(v, w)} \geq \frac{1}{2 \ln n} d \frac{2}{3 d}\\ &=\frac{1}{3 \ln n} = O\left(\frac{1}{\ln n}\right) \end{aligned} \]

其中對\(\sum_{w \in I} \frac{1}{d(v, w)}\)，我們考慮到所有項都有\(\frac{1}{d(v, w)}\geq \frac{2}{3d}\)，故在此基礎上進行放縮。

因此，我們有\(v\)連結到\(t\)周圍\(I\)間隔（寬度為\(\frac{d}{2}\)）內的概率為（這裡\(d=d(v,t)\)）

\[\text{P}(v \text { points to } I)=O(\frac{1}{\ln n}) \]

得證。

這實際上就意味著在期望上我們只需要步數\(\sharp \text{step}\leqslant \ln(n)\)就能到達間隔\(I\)，因此就將到\(t\)的距離削減了一半。而距離被減半最多\(\log_2(n)\)次，故到達\(t\)的期望時間為\(O(\log_2(n)^2)\)。

注: 事實上在2D網格的情況下，我們有距離目標距離在\(d/2\)以內的節點數語\(d^2\)成比例，即\(\sharp nodes(I)∝ d^2\)。這表明要獲得和一維情況下同樣的「抵消」效果，需要\(v\)連線到每個其它節點\(w\)的概率應該與\(d(v,w)^{-2}\)成比例，這樣我們也有結論\(\text P(v \text { points to } I)>\ln{n}\)。

3.4 多種模型的搜尋時間對比和反思

總結一下，不可搜尋的模型對應的搜尋時間為\(O(n^{\lambda})\)，其代表為Watts-Stogatz網路(\(O(n^{\frac{2}{3}})\))、Erdős-Rényi網路(\(O(n)\))；可搜尋模型對應的搜尋時間為\(O((\log n)^{\gamma})\)，其代表為Kleinberg模型(\(O(\log_2(n)^2)\))。

由於小世界圖的直徑為\(O(\log n)\)，故Kleinberg模型的搜尋時間關於\(\log n\)是多項式階增長的，然而Watts-Stogatz模型關於\(\log n\)是指數階增長的。

前面我們已經證明，在一維情況下當距離節點距離項\(\mathrm{d}(\mathrm{u}, \mathrm{v})^{-\alpha}\)中的\(\alpha=0\)時（也即Watts-Strogatz模型），我們需要\(O（\sqrt{n}）\)步，當\(\alpha=1\)時，我們需要\(O(\log(n)^2)\)步。事實上，我們有搜尋時間和指數\(\alpha\)的關係如下：

可見當\(\alpha=2\)時分散搜尋最有效（此時隨機連結遵循反平方分佈）。

過小和過大的\(\alpha\)形象化的展示如下圖所示：

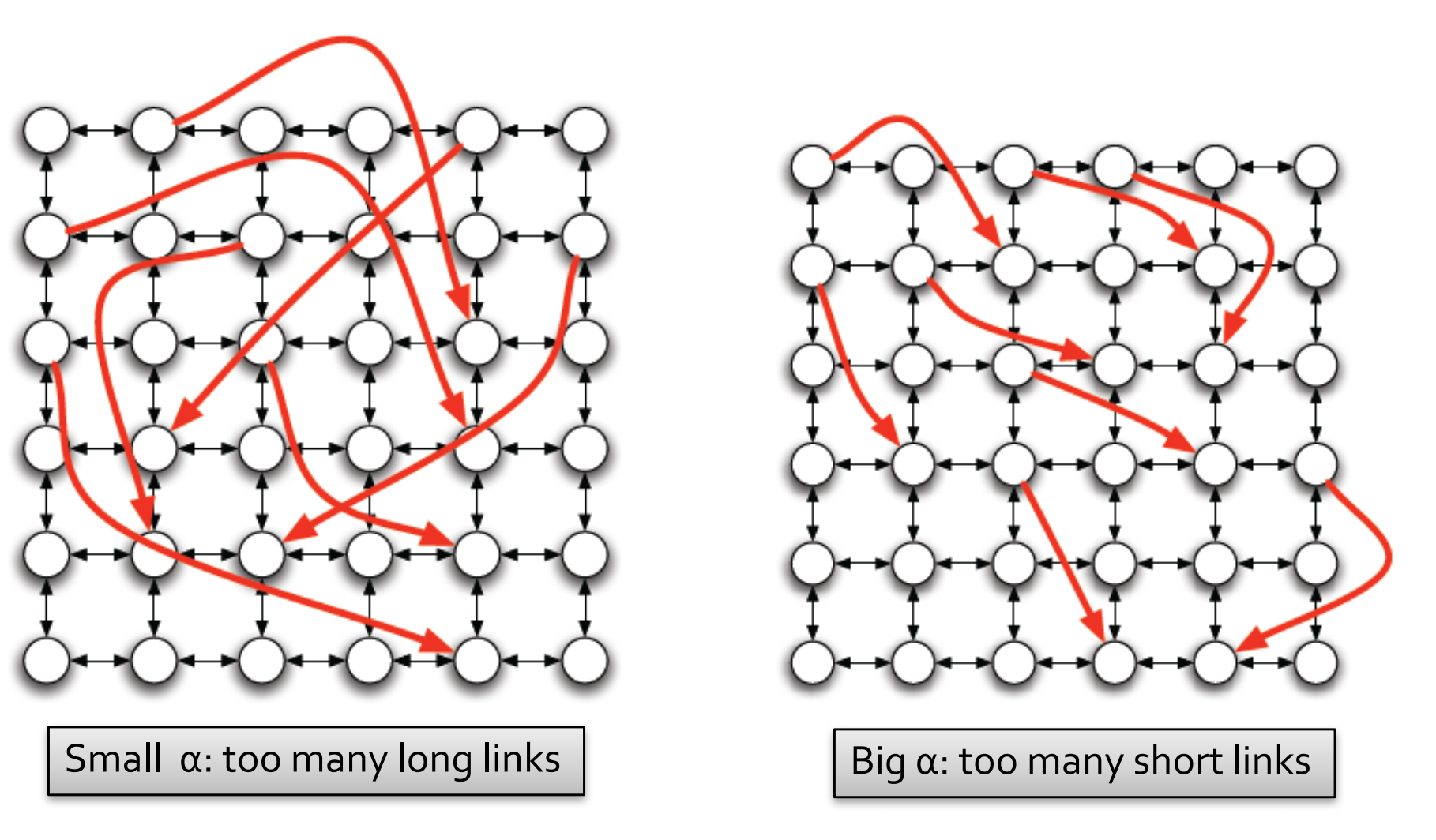
可接過小的\(\alpha\)意味著有太多的長距離連結，過大的\(\alpha\)則意味著又太多的短距離連結。

最後，讓我們來思考一下為什麼\(P(u \rightarrow v) \sim d(u, v)^{d i m}\)會如此有效呢？因為該分佈在所有「解析度尺度」上都是近似均勻的，和\(u\)之間距離為\(d\)的節點數量會以\(d^{dim}\)倍率增長，而這會產生一種抵消作用，導致每條邊產生連結的概率值和\(d\)獨立（正如我們前面分析二維情況時所說）。如下圖所示：

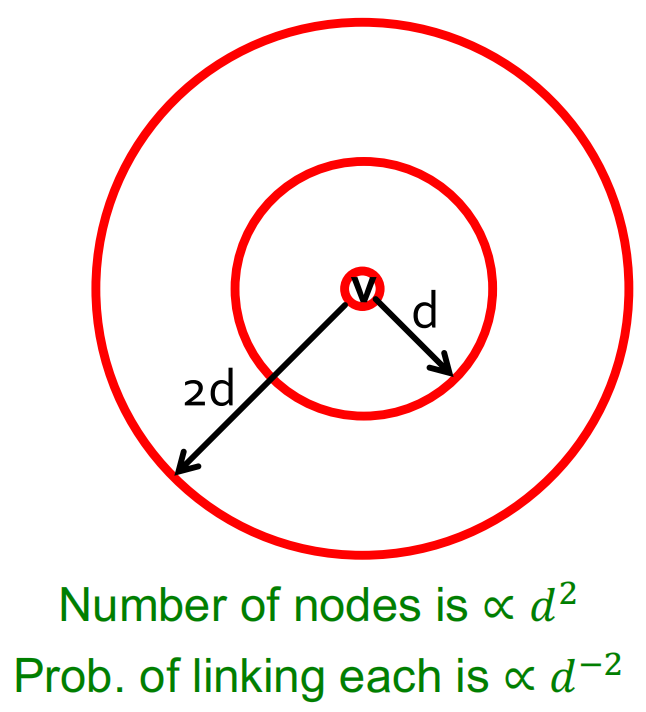
參考

[1] Milgram S. The small world problem[J]. Psychology today, 1967, 2(1): 60-67.
[2] Watts D J, Strogatz S H. Collective dynamics of ‘small-world’networks[J]. nature, 1998, 393(6684): 440-442.
[3] Kleinberg J. The small-world phenomenon: An algorithmic perspective[C]//Proceedings of the thirty-second annual ACM symposium on Theory of computing. 2000: 163-170.
[4] http://web.stanford.edu/class/cs224w/
[5] Easley D, Kleinberg J. Networks, crowds, and markets: Reasoning about a highly connected world[M]. Cambridge university press, 2010.
[6] Barabási A L. Network science[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 371(1987): 20120375.

圖資料探勘：小世界網路模型和分散式搜尋