經典揹包系列問題
經典揹包系列問題
作者:Grey
原文地址:
問題一
題目描述
在 n 個物品中挑選若干物品裝入揹包,最多能裝多滿?假設揹包的大小為m,每個物品的大小為Ai (每個物品只能選擇一次且物品大小均為正整數)
題目連結:LintCode 92 · Backpack
暴力遞迴方法思路
定義遞迴函數
int p(int rest, int i, int[] arr)
遞迴含義表示:從 i 開始到最後,還剩下 rest 容量的情況下,得到的最大值是多少。
遞迴函數中有兩個決策,第一個決策,不要當前位置物品
int p1 = p(rest, i+1, arr);
第二個決策,要當前物品,這個決策下,有一個限制條件,即當前物品大小不超過 rest,
arr[i] + p(rest - arr[i], i + 1, arr)
暴力解法的完整程式碼如下
public class Solution {
public static int backPack(int m, int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
return p(m, 0, arr);
}
public static int p(int i, int j, int[] arr) {
if (j == arr.length) {
return 0;
}
int p1 = p(i, j + 1, arr);
return i >= arr[j] ? Math.max(arr[j] + p(i - arr[j], j + 1, arr), p1) : p1;
}
}
超時
優化一,可以通過快取法來對上述遞迴過程進行優化,由於遞迴函數只有兩個可變引數,所以可以定義一個二維陣列 dp,二維陣列的元素全部初始化為 -1,表示未計算過,用這個二維陣列就可以存下所有的遞迴過程中間值,在遞迴函數中,如果 dp 的值已經計算過,直接返回即可。在每次遞迴結果返回之前,要先把結果存入 dp 對應的位置,快取法的完整程式碼和註釋說明如下:
public class Solution {
public static int backPack(int m, int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
int[][] dp = new int[arr.length + 1][m + 1];
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[0].length; j++) {
dp[i][j] = -1;
}
}
return p2(m, 0, arr, dp);
}
public static int p2(int rest, int i, int[] arr, int[][] dp) {
// 計算過,直接返回即可
if (dp[i][rest] != -1) {
return dp[i][rest];
}
int ans = 0;
if (i == arr.length) {
// 每次計算的結果在返回之前,先更新 dp 值
dp[i][rest] = ans;
return ans;
}
int p1 = p2(rest, i + 1, arr, dp);
ans = rest >= arr[i] ? Math.max(arr[i] + p2(rest - arr[i], i + 1, arr, dp), p1) : p1;
// 每次計算的結果在返回之前,先更新 dp 值
dp[i][rest] = ans;
return ans;
}
}
可 AC。
優化二,除了上述快取法,也可以將暴力遞迴方法直接改成嚴格位置依賴的動態規劃,設定一個 dp 陣列
int[][] dp = new int[arr.length + 1][m + 1]
其中 dp[i][j] 就表示遞迴函數 p(i,j,arr) 的值,根據暴力遞迴方法可知
dp[i][j] 依賴的位置是 dp[i][j+1] 以及 dp[i - arr[j]][j + 1] 兩個位置的值,完整程式碼如下
public class Solution {
public static int backPack(int m, int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
int[][] dp = new int[arr.length + 1][m + 1];
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = 0; j < m + 1; j++) {
int p1 = dp[i + 1][j];
dp[i][j] = j >= arr[i] ? Math.max(arr[i] + dp[i + 1][j - arr[i]], p1) : p1;
}
}
return dp[0][m];
}
}
可 AC。
優化三,上述動態規劃的轉移過程如下
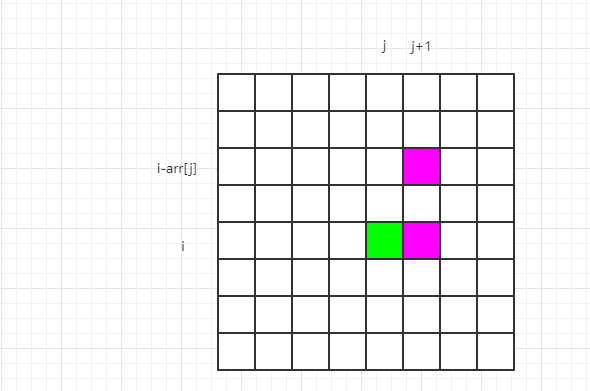
其中 dp[i][j] 依賴的位置是 dp[i][j+1] 以及 dp[i - arr[j]][j + 1] 兩個位置,根據這個依賴關係,可以將二維陣列簡化成一維陣列,
設定一維陣列
int[] dp = new int[m + 1];
先求最後一列的值,然後複用這個陣列推出倒數第二列的值。最後推到第一列的值,完整程式碼
public class Solution {
public static int backPack(int m, int[] arr) {
if (arr == null || arr.length < 1) {
return 0;
}
int[] dp = new int[m + 1];
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = m; j >= 0; j--) {
if (j >= arr[i]) {
dp[j] = Math.max(dp[j - arr[i]] + arr[i], dp[j]);
}
}
}
return dp[m];
}
}
問題二
問題描述
有 n 個物品和一個大小為 m 的揹包. 給定陣列 A 表示每個物品的大小和陣列 V 表示每個物品的價值,問最多能裝入揹包的總價值是多大?
題目連結:LintCode 125 · Backpack II
暴力解法
定義遞迴函數
int process(int i, int m, int[] w, int[] v)
遞迴含義表示:i 號及其往後所有的物品在重量允許範圍內的最大價值是多少。
首先是 base case
if (i == w.length) {
return 0;
}
表示無物品可選,返回 0 的價值。
接下來是普遍情況,有兩種決策,
決策一:選擇 i 位置的物品,則
int p1 = process(i + 1, m, w, v);
決策二,不選擇 i 位置的物品,此時有條件,即物品重量不能超過當前書包的剩餘容量,即
v[i] + process(i + 1, m - w[i], w, v)
完整程式碼如下
public class Solution {
public static int backPackII(int m, int[] w, int[] v) {
if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
return 0;
}
return process(0, m, w, v);
}
// i號及其往後所有的物品在重量允許範圍內的最大價值是多少
public static int process(int i, int m, int[] w, int[] v) {
if (i == w.length) {
return 0;
}
// 不選i號商品
int p1 = process(i + 1, m, w, v);
if (m >= w[i]) {
// 這種情況下,才有資格選i號商品
return Math.max(p1, v[i] + process(i + 1, m - w[i], w, v));
}
return p1;
}
}
超時
優化一,增加快取,使用一個二維陣列 dp 來儲存遞迴過程的中間值
int[][] dp = new int[w.length + 1][m + 1];
dp 的初始值全為 -1, 同時,將每次遞迴結果都存入 dp 中,如果某個遞迴算過了,則直接返回即可,完整程式碼如下
public class Solution {
public static int backPackII(int m, int[] w, int[] v) {
if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
return 0;
}
int[][] dp = new int[w.length + 1][m + 1];
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[0].length; j++) {
dp[i][j] = -1;
}
}
return process2(0, m, w, v, dp);
}
public static int process2(int i, int m, int[] w, int[] v, int[][] dp) {
if (dp[i][m] != -1) {
return dp[i][m];
}
if (i == w.length) {
dp[i][m] = 0;
return 0;
}
// 最後一行都是0
// 從最後一行開始
int ans = process2(i + 1, m, w, v, dp);
if (i < w.length && m >= w[i]) {
// 這種情況下,才有資格選i號商品
ans = Math.max(ans, v[i] + process2(i + 1, m - w[i], w, v, dp));
}
dp[i][m] = ans;
return ans;
}
}
可 AC
優化二,由於暴力遞迴過程只有兩個可變引數,所以本問題也可以改成嚴格位置的動態規劃解,定義一個二維陣列 dp,
int[][] dp = new int[w.length + 1][m + 1];
通過觀察暴力遞迴過程可知,dp[i][j] 依賴 dp[i+1][j] 和 dp[i+1][j-w[i]] 兩個位置的值,完整程式碼如下
public class Solution {
public static int backPackII(int m, int[] w, int[] v) {
if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
return 0;
}
int[][] dp = new int[w.length + 1][m + 1];
// 倒數第一行都是0
// 從倒數第二行開始填
for (int i = w.length - 1; i >= 0; i--) {
for (int j = m; j >= 0; j--) {
dp[i][j] = dp[i + 1][j];
if (j >= w[i]) {
dp[i][j] = Math.max(dp[i][j], v[i] + dp[i + 1][j - w[i]]);
}
if (j == m && i == 0) {
break;
}
}
}
return dp[0][m];
}
}
優化四,參考問題1,上述動態規劃也可以做進一步的空間壓縮,使用一個一維陣列來捲動更新,不贅述,完整程式碼如下
public class Solution {
public static int backPackII(int m, int[] w, int[] v) {
if (m <= 0 || w == null || w.length < 1 || v == null || v.length < 1) {
return 0;
}
int[] dp = new int[m + 1];
for (int i = w.length - 1; i >= 0; i--) {
for (int j = m; j >= 0; j--) {
if (j >= w[i]) {
dp[j] = Math.max(dp[j], v[i] + dp[j - w[i]]);
}
if (i == 0) {
break;
}
}
}
return dp[m];
}
}
更多
本文來自部落格園,作者:Grey Zeng,轉載請註明原文連結:https://www.cnblogs.com/greyzeng/p/16851959.html