如何使用並查集解決朋友圈問題?
本文已收錄到 GitHub · AndroidFamily,有 Android 進階知識體系,歡迎 Star。技術和職場問題,請關注公眾號 [彭旭銳] 私信我提問。
前言
大家好,我是小彭。
今天分享到的是一種相對冷門的資料結構 —— 並查集。雖然冷門,但是它背後體現的演演算法思想卻非常精妙,在處理特定問題上能做到出奇制勝。那麼,並查集是用來解決什麼問題的呢?
學習路線圖:
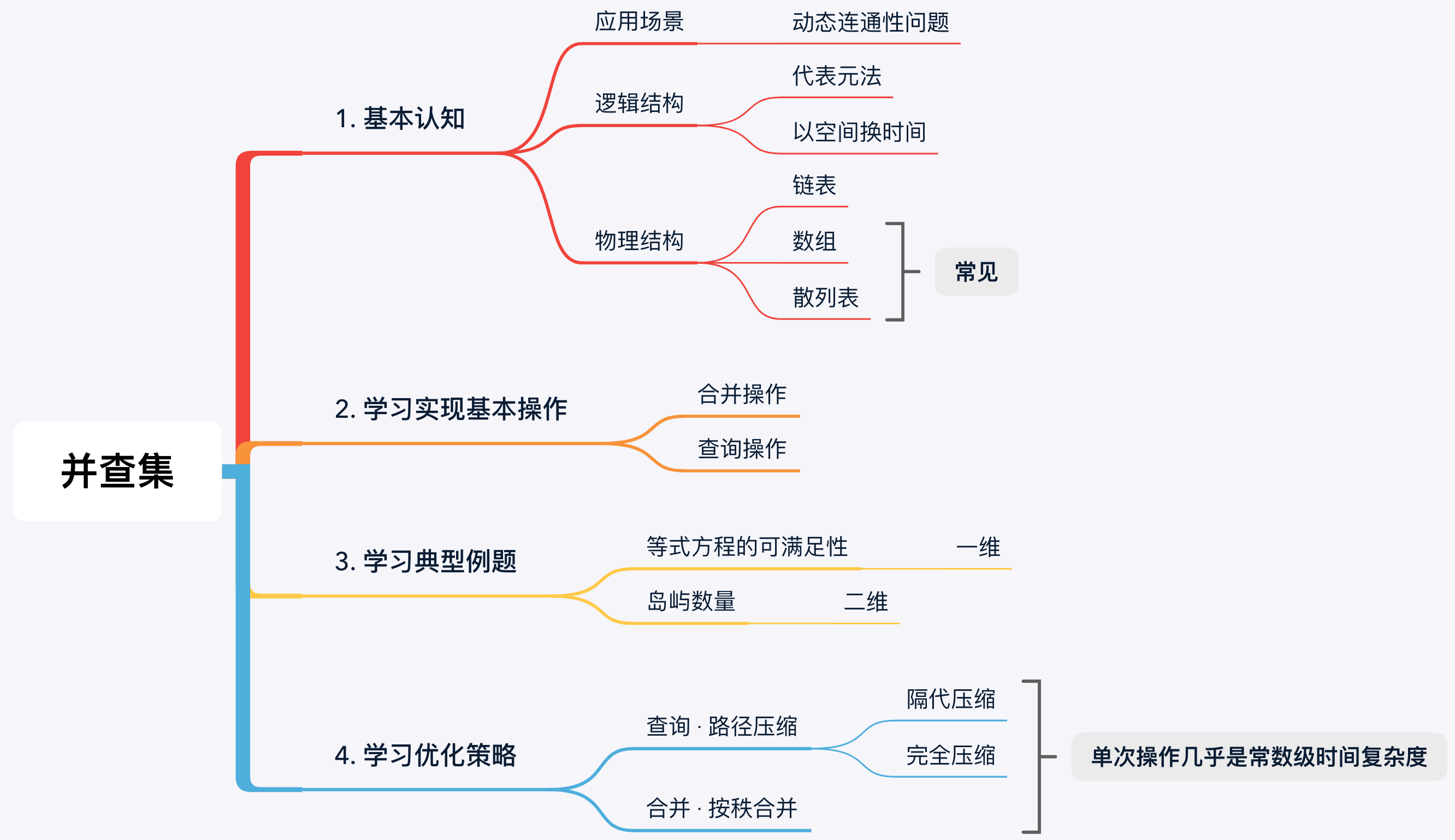
1. 認識並查集
除了並查集之外,不相交集合(Disjoint Sets)、合併-查詢集合(Merge-find Set)、聯合-查詢資料結構(Union-find Data Structure)、聯合-查詢演演算法(Union-find algorithm),均表示相同的資料結構或思想。
1.1 並查集用於解決什麼問題?
並查集是一種用來高效地判斷 「動態連通性 」 的資料結構: 即給定一個無向圖,要求判斷某兩個元素之間是否存在相連的路徑(連通),這就是連通問題,也叫 「朋友圈」 問題。聽起來有點懵,你先彆著急哈,咱來一點一點地把這個知識體系建立起來。
先舉個例子,給定一系列航班資訊,問是否存在 「北京」 到 「廣州」 的路徑,這就是連通性問題。而如果是問 「北京」 到 「廣州」 的最短路徑,這就是路徑問題。並查集是專注於解決連通性問題的資料結構,而不關心元素之間的路徑與距離,所以最短路徑等問題就超出了並查集的能夠處理的範圍,不是它考慮的問題。
連通問題與路徑問題示意圖
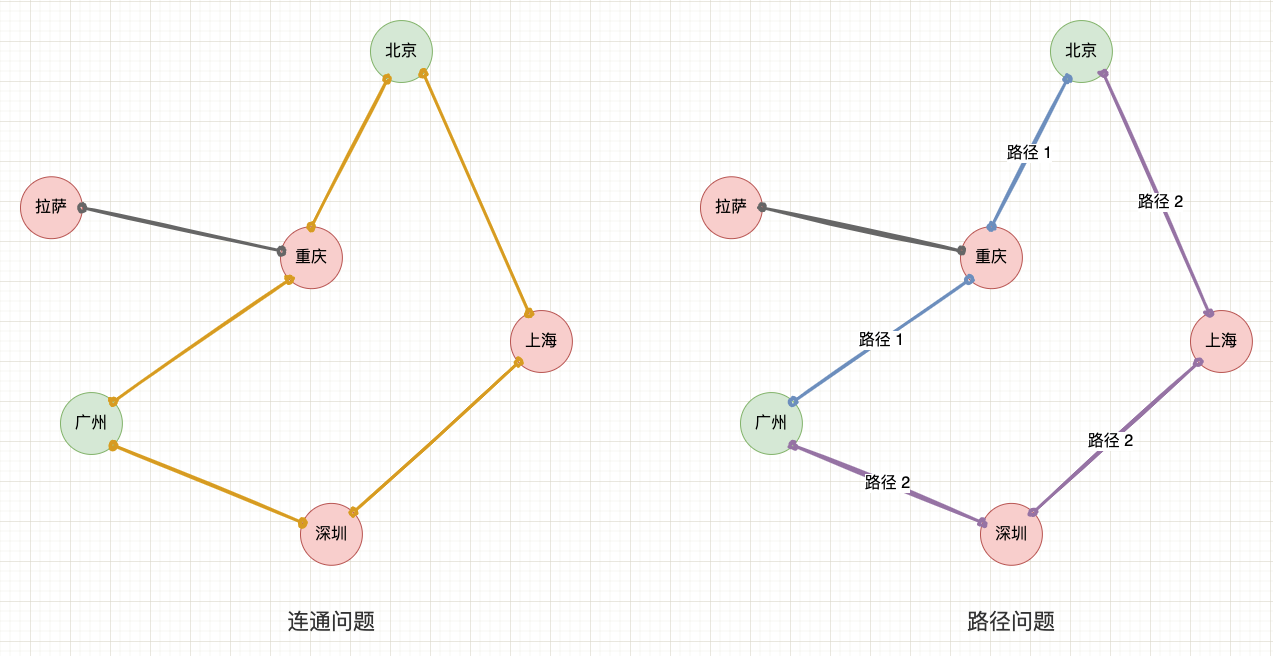
另一個關鍵點是,並查集也非常適合處理動態資料的連通性問題。 因為在完成舊資料的處理後,舊資料的連通關係是記錄在並查集中的。即使後續動態增加新的資料,也不需要重新檢索整個資料集,只需要將新資料提供的資訊補充到並查集中,這帶有空間換時間的思想。
動態連通問題

理解了並查集的應用場景後,下面討論並查集是如何解決連通性的問題。
1.2 並查集的邏輯結構
既然要解決連通性問題,那麼在並查集的邏輯結構裡,就必須用某種方式體現出兩個元素或者一堆元素之間的連線關係。那它是怎麼體現的呢 —— 代表元法。
並查集使用 「代表元法」 來表示元素之間的連線關係:將相互連通的元素組成一個子集,並從中選取一個元素作為代表元。而判斷兩個元素之間是否連通,就是判斷它們的代表元是否相同,代表元相同則說明處於相同子集,代表元不同則說明處於不同的子集。
例如,我們將航班資訊構建為並查集的資料結構後,就有 「重慶」 和 「北京」 兩個子集。此時,問是否存在 「北京」 到 「廣州」 的路徑,就是看 「北京」 和 「廣州」 的代表元是否相同。可見它們的代表元是相同的,因此它們是連通的。
並查集的邏輯結構和物理結構

理解了並查集的邏輯結構後,下面討論如何用程式碼實現並查集。
1.3 並查集的物理結構
並查集的物理結構可以是陣列,亦可以是連結串列,只要能夠體現節點之間連線關係即可。
- 連結串列實現: 為每個元素建立一個連結串列節點,每個節點持有指向父節點的指標,通過指標的的指向關係來構建集合的連線關係,而根節點(代表元)的父節點指標指向節點本身;
- 陣列實現: 建立與元素個數相同大小的陣列,每個陣列下標與每個元素一一對應,陣列的值表示父節點的下標位置,而根節點(代表元)所處位置的值就是陣列下標,表示指向本身。
陣列實現相對於連結串列實現更加常見,另外,在陣列的基礎上還衍生出雜湊表的實現,關鍵看元素個數是否固定。例如:
- 在 LeetCode · 990. 等式方程的可滿足性 這道題中,節點是已知的 26 個字母,此時使用陣列即可;
- 在 LeetCode · 684. 冗餘連線 這道題中,節點個數是未知的,此時使用雜湊表更合適。
提示: 我們這裡將父節點指向節點本身定義為根節點,也有題解將父節點指向
null或者-1的節點定義為根節點。兩種方法都可以,只要能夠區分出普通節點和根節點。但是指向節點本身的寫法更簡潔,不需要擔心Union(x, x)出現死迴圈。
以下為基於陣列和基於雜湊表的程式碼模板:
基於陣列的並查集
// 陣列實現適合元素個數固定的場景
class UnionFind(n: Int) {
// 建立一個長度為 n 的陣列,每個位置上的值初始化陣列下標,表示初始化時有 n 個子集
private val parent = IntArray(n) { it }
...
}
基於雜湊表的並查集
// 雜湊表實現適合元素個數不固定的場景
class UnionFind() {
// 建立一個空雜湊表,
private val parent = HashMap<Int, Int>()
// 查詢操作
fun find(x: Int): Int {
// 1. parent[x] 為 null 表示首次查詢,先加入雜湊表中並指向自身
if (null == parent[x]) {
parent[x] = x
return x
}
// 下文說明查詢操作細節...
}
}
2. 並查集的基本概念
2.1 合併操作與查詢操作
「並查集,並查集」,顧名思義並查集就是由 「並」 和 「查」 這兩個最基本的操作組成的:
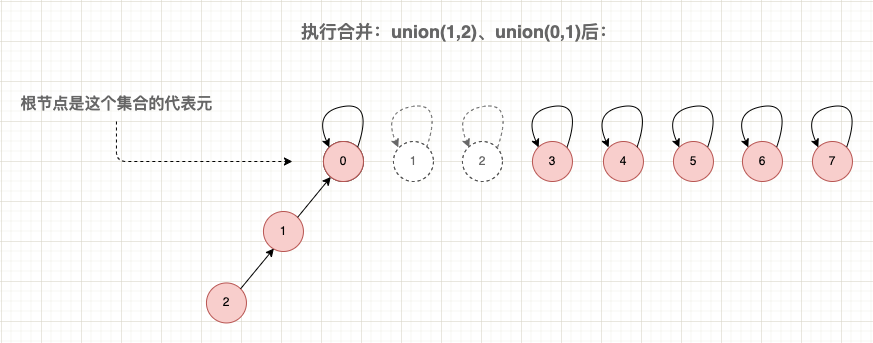
- Find 查詢操作: 沿著只用鏈條找到根節點(代表元)。如果兩個元素的根節點相同,則說明兩個元素是否屬於同一個子集,否則屬於不同自己;
- Union 合併操作: 將兩個元素的根節點合併,也表示將兩個子集合併為一個子集。
例如,以下是一個基於陣列的並查集實現,其中使用 Find(x) 查詢元素的根節點使用 Union(x, y) 合併兩個元素的根節點:
基於陣列的並查集
class UnionFind(n: Int) {
// 建立一個長度為 n 的陣列,每個位置上的值初始化陣列下標,表示初始化時有 n 個子集
val parent = IntArray(n) { it }
// 查詢操作(遍歷寫法)
fun find(x: Int): Int {
var key = x
while (key != parent[key]) {
key = parent[key]
}
return key
}
// 合併操作
fun union(x: Int, y: Int) {
// 1. 分別找出兩個元素的根節點
val rootX = find(x)
val rootY = find(y)
// 2. 任意選擇其中一個根節點成為另一個根節點的子樹
parent[rootY] = rootX
}
// 判斷連通性
fun isConnected(x: Int, y: Int): Boolean {
// 判斷根節點是否相同
return find(x) == find(y)
}
// 查詢操作(遞迴寫法)
fun find(x: Int): Int {
var key = x
if (key != parent[key]) {
return find(parent[key])
}
return key
}
}
合併與查詢示意圖
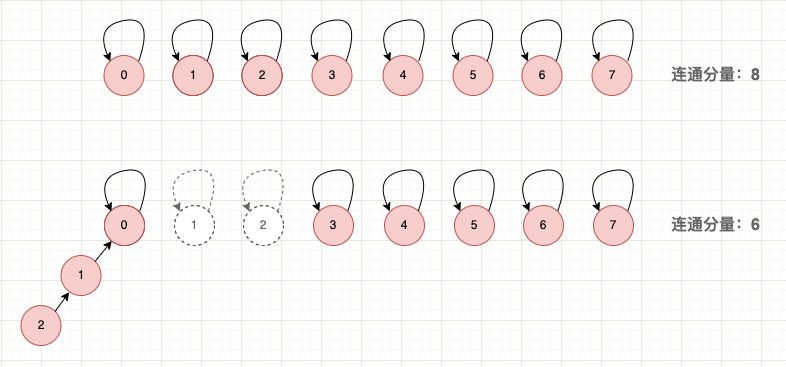
2.2 連通分量
並查集的連通分量,表示的是整個並查集中獨立的子集個數,也就是森林中樹的個數。要計算並查集的連通分量,其實就是在合併操作中維護連通分量的計數,在合併子集後將計數減一。
class UnionFind(n: Int) {
private val parent = IntArray(n) { it }
// 連通分量計數,初始值為元素個數 n
var count = n
// 合併操作
fun union(x: Int, y: Int) {
val rootX = find(x)
val rootY = find(y)
if(rootX == rootY){
// 未發生合併,則不需要減一
return
}
// 合併後,連通分量減一
parent[rootY] = rootX
count --
}
...
}
連通分量示意圖
3. 典型例題 · 等式方程的可滿足性
理解以上概念後,就已經具備解決連通問題的必要知識了。我們看一道 LeetCode 上的典型例題: LeetCode · 990.
LeetCode 例題
我們可以把每個變數看作一個節點,而等式表示兩個節點相連,不等式則表示兩個節點不相連。那麼,我們可以分 2 步:
- 1、先遍歷所有等式,將等式中的兩個變數合併到同一個子集中,最終構造一個並查集;
- 2、再遍歷所有不等式,判斷不等式中的兩個變數是否處於同一個子集。是則說明有衝突,即等式方程不成立。
—— 圖片參照自 LeetCode 官方題解
題解範例如下:
題解
// 未優化版本
class Solution {
fun equationsPossible(equations: Array<String>): Boolean {
// 26 個小寫字母的並查集
val unionFind = UnionFind(26)
// 合併所有等式
for (equation in equations.filter { it[1] == '=' }) {
unionFind.union(equation.first(), equation.second())
}
// 檢查不等式是否與連通性衝突
for (equation in equations.filter { it[1] == '!' }) {
if (unionFind.isConnected(equation.first(), equation.second())) {
return false
}
}
return true
}
private fun String.first(): Int {
return this[0].toInt() - 97
}
private fun String.second(): Int {
return this[3].toInt() - 97
}
private class UnionFind() {
// 程式碼略
}
}
4. 並查集的優化
前面說到並查集邏輯上是一種基於森林的資料結構。既然與樹有關,我們自然能想到它的複雜度就與樹的高度有關。在極端條件下(按照特殊的合併順序),有可能出現樹的高度恰好等於元素個數 n 的情況,此時,單次 Find 查詢操作的時間複雜度就退化到 $O(n)$。
那有沒有優化的辦法呢?
4.1 父節點重要嗎?
在介紹具體的優化方法前,我先提出來一個問題:在已經選定集合的代表元后,一個元素的父節點是誰還重要嗎?答案是不重要。
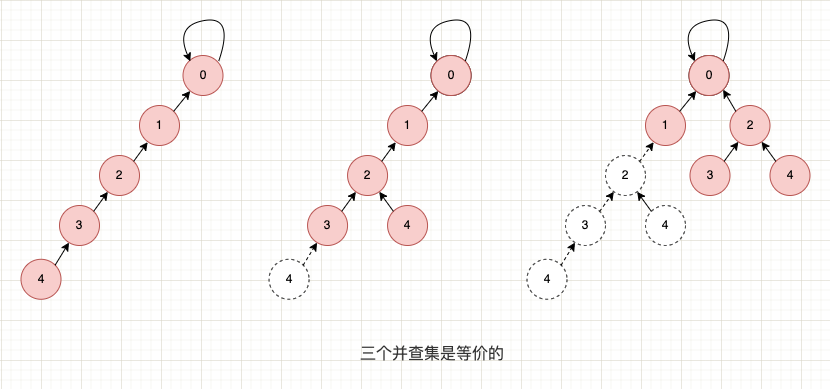
因為無論父節點是誰,最終都是去找根節點的。至於中間是經過哪些節點到達根節點的,這個並不重要。舉個例子,以下 3 個並查集是完全等價的,但明顯第 3 個並查集中樹的高度更低,查詢的時間複雜度更好。
父節點並不重要
理解了這個點之後,再理解並查集的優化策略就容易了。在並查集裡,有 2 種防止連結串列化的優化策略 —— 路徑壓縮 & 按秩合併。
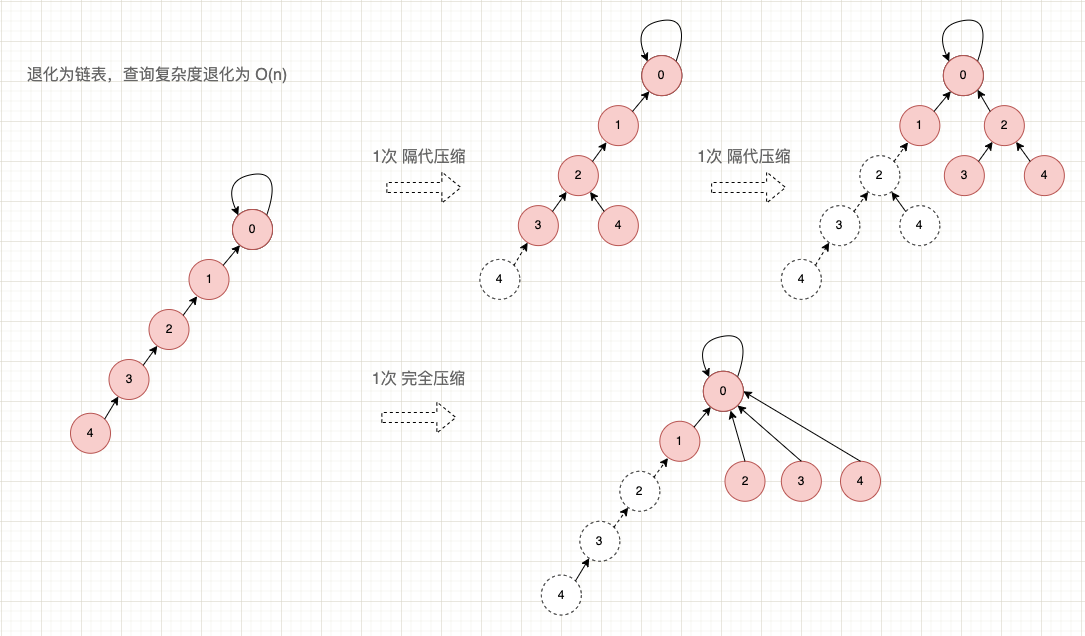
4.2 路徑壓縮(Path Compression)
路徑壓縮指在查詢的過程中,逐漸調整父節點的指向,使其指向更高層的節點,使得很多深層的階段逐漸放到更靠近根節點的位置。 根據調整的激程序度又分為 2 種:
- 隔代壓縮: 調整父節點的指向,使其指向父節點的父節點;
- 完全壓縮: 調整父節點的指向,使其直接指向根節點。
路徑壓縮示意圖
路徑壓縮範例程式
// 遍歷寫法
fun find(x: Int): Int {
var key = x
while (key != parent[key]) {
parent[key] = parent[parent[key]]
key = parent[key]
}
return key
}
// 遞迴寫法
fun find(x: Int): Int {
var key = x
if (key != parent[key]) {
parent[key] = find(parent[key])
return parent[key]
}
return key
}
4.3 按秩合併(Union by Rank)
在 第 2.1 節 提到合併操作時,我們採取的合併操作是相對隨意的。我們在合併時會任意選擇其中一個根節點成為另一個根節點的子樹,這就有可能讓一棵較大子樹成為較小子樹的子樹,使得樹的高度增加。
而按秩合併就是要打破這種隨意性,在合併的過程中讓較小的子樹成為較大子樹的子樹,避免合併以後樹的高度增加。 為了表示樹的高度,需要維護使用 rank 陣列,記錄根節點對應的高度。
按秩合併示意圖

按秩合併範例程式
private class UnionFind(n: Int) {
// 父節點
private val parent = IntArray(n) { it }
// 節點的高度
private val rank = IntArray(n) { 1 }
// 連通分量
var count = n
private set
// 查詢(路徑壓縮)
fun find(x: Int): Int {
var key = x
while (key != parent[key]) {
parent[key] = parent[parent[key]]
key = parent[key]
}
return key
}
// 合併(按秩合併)
fun union(key1: Int, key2: Int) {
val root1 = find(key1)
val root2 = find(key2)
if (root1 == root2) {
return
}
if (rank[root1] > rank[root2]) {
// root1 的高度更大,讓 root2 成為子樹,樹的高度不變
parent[root2] = root1
} else if (rank[root2] > rank[root1]) {
// root2 的高度更大,讓 root1 成為子樹,樹的高度不變
parent[root1] = root2
} else {
// 高度相同,誰當子樹都一樣
parent[root1] = root2
// root2 的高度加一
rank[root2]++
// 或
// parent[root2] = root1
// rank[root1] ++
}
count--
}
}
4.4 優化後的時間複雜度分析
在同時使用路徑壓縮和按秩合併兩種優化策略時,單次合併操作或查詢操作的時間複雜度幾乎是常數,整體的時間複雜度幾乎是線性的。
以對 N 個元素進行 N - 1 次合併和 M 次查詢的操作序列為例,單次操作的時間複雜度是 $O(a(N))$,而整體的時間複雜度是 $O(M·a(N))$。其中 $a(x)$ 是逆阿克曼函數,是一個增長非常非常慢的函數,只有使用那些非常大的 「天文數位」 作為變數 $x$,否則 $a(x)$ 的取值都不會超過 4,基本上可以當作常數。
然而,逆阿克曼函數畢竟不是常數,因此我們不能說並查集的時間複雜度是線性的,但也幾乎是線性的。關於並查集時間複雜度的論證過程,具體可以看參考資料中的兩本演演算法書籍,我是看不懂的。
5. 典型例題 · 島嶼數量(二維)
前面我們講的是一維的連通性問題,那麼在二維世界裡的連通性問題,並查集還依舊好用嗎?我們看 LeetCode 上的另一道典型例題: LeetCode · 200.
LeetCode 例題

這個問題直接上 DFS 廣度搜尋自然是可以的:遍歷二維陣列,每找到 1 後使用 DFS 遍歷將所有相連的 1 消除為 0,直到整塊相連的島嶼都消除掉,記錄島嶼數 +1。最後,輸出島嶼數。
用並查集的來解的話,關鍵技巧就是建立長度為 M * N 的並查集:遍歷二維陣列,每找到 1 後,將它與右邊和下邊的 1 合併起來,最終輸出並查集中連通分量的個數,就是島嶼樹。
並查集解法
class Solution {
fun numIslands(grid: Array<CharArray>): Int {
// 位置
fun position(row: Int, column: Int) = row * grid[0].size + column
// 並查集
val unionFind = UnionFind(grid)
// 偏移量陣列(向右和向下)
val directions = arrayOf(intArrayOf(0, 1), intArrayOf(1, 0))
// 邊界檢查
fun checkBound(row: Int, column: Int): Boolean {
return (row in grid.indices) and (column in grid[0].indices)
}
for (row in grid.indices) {
for (column in grid[0].indices) {
if ('1' == grid[row][column]) {
// 消費(避免後續的遍歷中重複搜尋)
grid[row][column] = '0'
for (direction in directions) {
val newRow = row + direction[0]
val newColumn = column + direction[1]
if (checkBound(newRow, newColumn) && '1' == grid[newRow][newColumn]) {
unionFind.union(position(newRow, newColumn), position(row, column))
}
}
}
}
}
return unionFind.count
}
private class UnionFind(grid: Array<CharArray>) {
// 父節點
private val parent = IntArray(grid.size * grid[0].size) { it }
// 節點高度
private val rank = IntArray(grid.size * grid[0].size) { 1 }
// 連通分量(取格子 1 的總數)
var count = grid.let {
var countOf1 = 0
for (row in grid.indices) {
for (column in grid[0].indices) {
if ('1' == grid[row][column]) countOf1++
}
}
countOf1
}
private set
// 合併(按秩合併)
fun union(key1: Int, key2: Int) {
val root1 = find(key1)
val root2 = find(key2)
if (root1 == root2) {
// 未發生合併,則不需要減一
return
}
if (rank[root1] > rank[root2]) {
parent[root2] = root1
} else if (rank[root2] > rank[root1]) {
parent[root1] = root2
} else {
parent[root1] = root2
rank[root2]++
}
// 合併後,連通分量減一
count--
}
// 查詢(使用路徑壓縮)
fun find(x: Int): Int {
var key = x
while (key != parent[key]) {
parent[key] = parent[parent[key]]
key = parent[key]
}
return key
}
}
}
6. 總結
到這裡,並查集的內容就講完了。文章開頭也提到了,並查集並不算面試中的高頻題目,但是它的設計思想確實非常妙。不知道你有沒有這種經歷,在看到一種非常美妙的解題 / 設計思想後,會不自覺地拍案叫絕,直呼內行,並查集就是這種。
更多同型別題目:
| 並查集 | 題解 |
|---|---|
| 990. 等式方程的可滿足性 | 【題解】 |
| 200. 島嶼數量 | 【題解】 |
| 547. 省份數量 | 【題解】 |
| 684. 冗餘連線 | 【題解】 |
| 685. 冗餘連線 II | |
| 1319. 連通網路的操作次數 | 【題解】 |
| 399. 除法求值 | |
| 952. 按公因數計算最大元件大小 | |
| 130. 被圍繞的區域 | |
| 128. 最長連續序列 | |
| 721. 賬戶合併 | |
| 765. 情侶牽手 |
參考資料
- 資料結構與演演算法分析 · Java 語言描述(第 8 章 · 不相互交集類)—— [美] Mark Allen Weiss 著
- 演演算法導論(第 21 章 · 用於不相交集合的資料結構)—— [美] Thomas H. Cormen 等 著
- 專題 · 並查集 —— LeetCode 出品
- 題目 · 等式方程的可滿足性 —— LeetCode 出品